迭代函数系统
在数学中,迭代函数系统 iterated function systems(IFS)是一种构造分形几何 Fractal的方法;产生的分形通常是自相似的。IFS分形与集合论的关系比分形几何更大。[1]它们于1981年被提出。
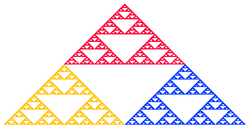
IFS分形,正如他们被通常称呼一样,可以是任何维度的,但通常在2维空间计算和绘制。分形是由其本身的几个副本的结合体组成,每个副本都由一个函数变换而成(因此称为 "函数系统")。典型的例子是谢尔宾斯基三角形 Sierpiński triangle。这些函数通常是收缩的,这意味着它们使点更接近,使形状更小。因此,IFS分形的形状是由若干个可能重叠的较小副本组成的,每个副本也是由自己的副本组成的,无穷无尽ad infinitum。这就是其自相似分形性质的来源。
定义
从形式上看,迭代函数系统是一个完整的度量空间上的有限收缩映射集。[2]符号表示为,
- [math]\displaystyle{ \{f_i:X\to X\mid i=1,2,\dots,N\},\ N\in\mathbb{N} }[/math]
如果每个[math]\displaystyle{ f_i }[/math]都是完整的度量空间[math]\displaystyle{ X }[/math]上的收缩,则是一个迭代函数系统。
性质

约翰·哈钦森 Hutchinson(1981)表明,对于度量空间[math]\displaystyle{ \lt mathbb{R}^n }[/math],或者更一般地说,对于一个完整的度量空间[math]\displaystyle{ X }[/math],这样的函数系统有一个唯一的非空紧凑(闭合且有界)的固定集S。构造固定集的一种方法是,从初始的非空的闭且有界集合S0开始,迭代fi的作用,取Sn+1为Sn在fi下的图像的联合;然后取S为Sn的联合的闭合。用符号可以表示为,唯一的固定(非空紧凑)集合[math]\displaystyle{ S\lt subseteq X }[/math]具有如下性质:
- [math]\displaystyle{ S = \overline{\bigcup_{i=1}^N f_i(S)}. }[/math]
集合S因此是Hutchinson算子的固定集。[math]\displaystyle{ F: 2^X/to 2^X }[/math]定义为[math]\displaystyle{ A/subseteq X }[/math],通过
- [math]\displaystyle{ F(A)=\overline{\bigcup_{i=1}^N f_i(A)}. }[/math]
S的存在性和唯一性是压缩映像原理的结果,就如
- [math]\displaystyle{ \lim_{n\to\infty}F^{\circ n}(A)=S }[/math]
对于[math]\displaystyle{ X }[/math]中的任何非空紧集[math]\displaystyle{ A }[/math]。(对于收缩型IFS,即使对于任何非空的闭合有界集[math]\displaystyle{ A }[/math],也会发生这种收敛。)。任意接近S的随机元素可以通过下面描述的 "chaos game "获得。
最近,人们证明了非收缩型的IFS(即由相对于X中的任何拓扑等价度量不收缩的映射组成)可以产生吸引子。
这些都是在投影空间中自然产生的,尽管经典的圆上的无理旋转也可以适应。[3]
函数的集合[math]\displaystyle{ f_i }[/math]能产生是运算下的独异点。如果只有两个这样的函数,那么这个单体可以可视化为一棵二叉树,在树的每一个节点上,我们可以用一个或另一个函数进行合成(即取左支或右支)。一般来说,如果有k个函数,那么可以将单子可视化为一个完整的k-ary树,也称为Cayley tree。
构建


有时,每个函数[math]\displaystyle{ f_i }[/math]都必须是线性变换,或者更一般的仿射变换,因此用矩阵表示。然而,IFS也可以由非线性函数建立,包括projective transformation和Möbius transformation。Fractal flame是一个非线性函数的IFS的例子。
计算IFS分形最常用的算法叫做“混沌游戏 chaos game”。它包括在平面上随机选取一个点,然后反复应用从函数系统中随机选取的一个函数来变换该点,去得到下一个点。另一种算法是生成每一个可能的函数序列,直到给定的最大长度,然后将这些函数序列中的每一个应用于初始点或形状的结果绘制出来。
这些算法中的每一种都提供了一个全局结构,生成分布在整个分形上的点。如果正在绘制分形的一小块区域,这些点中的许多将落在屏幕边界之外。这使得放大以这种方式绘制的IFS结构不切实际。
虽然IFS的理论要求每个功能都是收缩的,但实际上实现IFS的软件只要求整个系统平均是收缩的。[4]
分割迭代函数系统
分割迭代函数系统 partitioned iterated function systems(PIFS),也叫局部迭代函数系统,[5] 给出了令人惊讶的良好的图像压缩效果,即使是对于那些看起来不具有简单的IFS分形所显示的自相似结构的照片。[6]
逆问题
有非常快速的算法可以从一组IFS或PIFS参数生成图像。与存储和传输图像中每个像素的颜色相比,存储描述如何创建图像、将该描述传输到目标设备并在目标设备上重新生成图像的速度更快,所需的存储空间也更小。[5]
逆问题比较困难:给定一些原始的任意数字图像,如一张数字照片,试图找到一组IFS参数,通过迭代评估后,产生另一幅与原始图像视觉上相似的图像。在1989年,Arnaud Jacquin 提出了一个只用 PIFS 的限制形式的反问题的解,反问题的一般形式仍未解决。[7][8][5]并由迈克尔·巴恩斯利的著作《分形无处不在》而流行开来。1992年,斯科特·德拉维斯发明了分形火焰算法。截至1995年,所有分形压缩软件都是基于Jacquin的方法。[8]
范例
该图显示了两个仿射函数在IFS上的构造。这两个函数用它们对双单位正方形的影响来表示(函数将轮廓正方形转化为阴影正方形)。两个函数的组合形成Hutchinson算子。图中显示了该算子的三次迭代,然后是定点的最终图像,即最终的分形。
IFS可以生成分形的早期例子包括Cantor set,最早描述于1884年;de Rham curve,Georges de Rham在1957年描述的一种自相似曲线。
进一步阅读
- Complex-base system
- Collage theorem
- Infinite compositions of analytic functions
- L-system
- Fractal compression
参考文献
- ↑ Zobrist, George Winston; Chaman Sabharwal (1992). Progress in Computer Graphics: Volume 1. Intellect Books. p. 135. ISBN 9780893916510. https://play.google.com/store/books/details?id=Ai6Qo0qoE9EC. Retrieved 7 May 2017.
- ↑ Michael Barnsley (1988). Fractals Everywhere, p.82. Academic Press, Inc. ISBN 9780120790623.
- ↑ M. Barnsley, A. Vince, The Chaos Game on a General Iterated Function System
- ↑ Draves, Scott; Erik Reckase (July 2007). "The Fractal Flame Algorithm" (PDF). Archived from the original (pdf) on 2008-05-09. Retrieved 2008-07-17.
- ↑ 5.0 5.1 5.2 Bruno Lacroix. "Fractal Image Compression". 1998.
- ↑ Fischer, Yuval (1992-08-12). Przemyslaw Prusinkiewicz (ed.). SIGGRAPH'92 course notes - Fractal Image Compression (PDF). SIGGRAPH. Vol. Fractals - From Folk Art to Hyperreality. ACM SIGGRAPH.
- ↑ Dietmar Saupe, Raouf Hamzaoui."A Review of the Fractal Image Compression Literature".
- ↑ 8.0 8.1 John Kominek. "Algorithm for Fast Fractal Image Compression"
相关链接
- Draves, Scott; Erik Reckase (July 2007). "The Fractal Flame Algorithm" (PDF). Archived from the original (pdf) on 2008-05-09. Retrieved 2008-07-17.
- Falconer, Kenneth (1990). Fractal geometry: Mathematical foundations and applications. John Wiley and Sons. pp. 113–117, 136. ISBN 0-471-92287-0. https://archive.org/details/fractalgeometrym0000falc/page/113.
- Barnsley, Michael; Andrew Vince (2011). "The Chaos Game on a General Iterated Function System". Ergodic Theory Dynam. Systems. 31 (4): 1073–1079. arXiv:1005.0322. Bibcode:2010arXiv1005.0322B.
- For an historical overview, and the generalization : David, Claire (2019). "fractal properties of Weierstrass-type functions". Proceedings of the International Geometry Center. 12 (2): 43–61.
编辑推荐
书籍推荐
分形对象:形、机遇和维数 Fractals:From,Chance,and Dimension
本书考察和研究出现在自然界中的若干典型分形对象,为我们提供了一个关于分形的内容,意义及方法的扼要介绍。尽管自该书第一版(法文版)问世以来,分形的理论及其应用发展极为迅速,并出现了大量的有关著作,但此书仍不失为分形理论最好的入门书之一
大自然的分形几何 The Fractal Geometry of Nature
这本书介绍了自然界中各种各样的分形理论,从海岸线、雪花,到河流、星系等自然现象,去阐述分形这一概念。作为多个学科的交叉,分形几何对以往欧氏几何不屑一顾(或说无能为力)的“病态”曲线(如科赫雪花曲线等)的全新解释,是人类认识客观世界不断开拓的必然结果。这说明欧氏几何只是对客观世界的近似反映,而分形几何则深化了这种认识,因此分形几何学是描述各种复杂自然曲线的大自然的几何学。
市场的(错误)行为:风险、破产与收益的分形观点The Misbehavior of Markets: A Fractal View of Financial Turbulence
《市场的(错误)行为》以分形视角观察金融市场的行为,推翻了作为当代金融分析基础的“随机游走”理论。通过分形模型,市场表现被重新阐释。本书是现代金融理论标准工具和模型的一次革命性重估,书中的观点颠覆了成千上万投资者的既有观念。
网站资源
分形艺术网
分形艺术网是一个展示分形艺术之美,学习交流分形艺术创作的平台,其中包含了很多分形艺术作品及分形资源推荐。
视频资源
TED分享视频:伯努·瓦曼德布洛特: 分形和粗糙的艺术 Benoit Mandelbrot: Fractals and the Art of Roughness
Benoit Mandelbrot的研究使世界对分形有了更深刻的理解,分形是研究粗糙的广泛而有力的工具,在自然界和人类的作品中都是如此。该视频概述了分形的研究,以及它们为许多领域带来的颠覆性见解。
寻找隐藏的维 Hunting the Hidden Dimension
什么是电影特效,股票市场,和心脏病的共同点?它们连接了一个革命性的新的数学分支,改变了我们看世界,开辟了广阔的新领域,以科学的分析和理解。数学家们开发不规则碎片形是从单纯的好奇心到接触几乎每一个分科的理解,包括我们宇宙的命运。
课程推荐
分形与奇异吸引子的几何学
本课程对非线性动力学和混沌进行了详细的讲解,强调分析方法、具体实例和几何直觉。主讲人为Steven Strogatz。
分形的世界
在此堂课程,主要介绍了关于分形的思想与脉络,分形现象、分形维数、利用分形规律的计算方法以及混沌。主讲人为北京师范大学系统学院狄增如教授。狄增如教授主要从事复杂网络和经济(金融)物理学等方面的研究,是国内最早从事经济物理学研究的学者之一。
集智百科文章
本中文词条由Eatcosmos2编译,Inch审校,薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。