Do演算
Do演算 Do-Calculus于1995年由Judea Pearl提出[1],是由三条推演规则构成的推演系统,这三条规则可以将包含干预变量和观测变量的概率分布表达式进行转化。Do演算属于因果科学中结构因果模型的基础分析工具,可用于非参数模型中因果效应的识别,并能够在中介分析 Mediation Analysis、知识迁移 Transportability、元综合Metasynthesis等方向上发挥重要作用。
为何需要Do演算
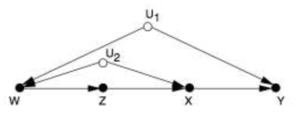
在处理一部分因果图时,可以使用后门调整后门调整和前门调整等技术进行统计调整,这样可以根据不涉及Do算子的数据来估算干预的效果。然而我们无法根据前门准则和后门准则事先确定一个给定的因果模型是否适用于这样的统计调整方式。后门调整和前门调整方法也无法处理所有可识别的模型,例如右侧的因果图是可识别的,但既无法使用后门调整也无法使用前门调整。
而Do演算是一个具有完备性的推演系统,可以处理所有可识别的模型,当然也就包括了右侧图中这个例子。同时,利用Do演算还有一系列的计算机算法,可以自动、高速地去判断一个模型的可识别性,并在可识别的模型中将包含Do算子的概率分布表达式转换为仅包含观测变量的概率分布表达式。
Do演算规则集
在以下规则的表述中,使用符号[math]\displaystyle{ G_{\overline{X}} }[/math]表示删除有向图[math]\displaystyle{ G }[/math]中所有指向结点[math]\displaystyle{ X }[/math]的边后得到的子图,使用符号[math]\displaystyle{ G_{\overline{X}\underline{Z}} }[/math]表示删除有向图[math]\displaystyle{ G }[/math]中所有指向结点[math]\displaystyle{ X }[/math]的边和从结点[math]\displaystyle{ Z }[/math]指出的边后得到的子图。
规则一
增添或删除观察:
对于有向图[math]\displaystyle{ G }[/math],若满足[math]\displaystyle{ (Y \perp\!\!\!\perp Z \mid X, W)_{G_{\overline{X}}} }[/math](即在子图[math]\displaystyle{ G_{\overline{X}} }[/math]中,给定结点集[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math]时,结点集[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]满足d-分离条件),则
- [math]\displaystyle{ P(Y|do(X),Z,W)=P(Y|do(X),W) }[/math]
规则二
交换干预和观察:
对于有向图[math]\displaystyle{ G }[/math],若满足[math]\displaystyle{ (Y \perp\!\!\!\perp Z \mid X, W)_{G_{\overline{X}\underline{Z}}} }[/math](即在子图[math]\displaystyle{ G_{\overline{X}\underline{Z}} }[/math]中,给定结点集[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math]时,结点集[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]满足d-分离条件),则
- [math]\displaystyle{ P(Y|do(X),do(Z),W)=P(Y|do(X),Z,W) }[/math]
规则三
增添或删除干预:
对于有向图[math]\displaystyle{ G }[/math],若满足[math]\displaystyle{ (Y \perp\!\!\!\perp Z \mid X, W)_{G_{\overline{X}\overline{Z(W)}}} }[/math](即在子图[math]\displaystyle{ G_{\overline{X}\overline{Z(W)}} }[/math]中,给定结点集[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math]时,结点集[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]满足d-分离条件),则
- [math]\displaystyle{ P(Y|do(X),do(Z),W)=P(Y|do(X),W) }[/math]
其中符号[math]\displaystyle{ Z(W) }[/math] 表示 [math]\displaystyle{ Z / An(W)_{ G_{ \overline{X} } } }[/math] ,而符号[math]\displaystyle{ An(W)_{ G_{ \overline{X} } } }[/math] 表示在子图[math]\displaystyle{ G_{ \overline{X}} }[/math]中由结点集[math]\displaystyle{ W }[/math]及其祖先节点构成的点集。
Do演算的完备性
定理
[math]\displaystyle{ Q = P(y \mid do(x),z) }[/math] 是可识别的,当且仅当它可以被Do演算的三条规则转化为一个不包含Do算子的表达式。
证明
要证明上述定理的正确性,需要分别证明Do演算的可靠性(Soundness)和充分性(Sufficiency)。其中可靠性的证明由Judea Pearl于1995年给出[1],充分性的证明由Yimin Huang和Marco Valtorta于2006年给出[2]。
应用案例
应用案例1
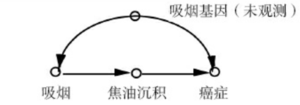
在右侧的因果图中,“吸烟基因”是未观测变量,其余变量都是可观测的。“吸烟”变量使用[math]\displaystyle{ s }[/math]来表示,“焦油沉积”变量使用[math]\displaystyle{ t }[/math]来表示,“癌症”变量使用[math]\displaystyle{ c }[/math]来表示。我们要估计干预“吸烟”变量后对“癌症”变量的因果效应,即计算[math]\displaystyle{ P(c \mid do(s)) }[/math]。我们将使用Do演算将这个表达式转换为不包含Do算子的表达式。
[math]\displaystyle{ \begin{alignat}{3} P(c \mid do(s)) & = \Sigma_t P(c \mid do(s), t)P(t \mid do(s)) & \text{(使用概率公理)} \\ & = \Sigma_t P(c \mid do(s), do(t))P(t \mid do(s)) & \text{(使用规则二)} \\ & = \Sigma_t P(c \mid do(s), do(t))P(t \mid s) & \text{(使用规则二)} \\ & = \Sigma_t P(c \mid do(t))P(t \mid s) & \text{(使用规则三)} \\ & = \Sigma_{s'}\Sigma_t P(c \mid do(t),s')P(s' \mid do(t))P(t \mid s) & \text{(使用概率公理)} \\ & = \Sigma_{s'}\Sigma_t P(c \mid t,s')P(s' \mid do(t))P(t \mid s) & \text{(使用规则二)} \\ & = \Sigma_{s'}\Sigma_t P(c \mid t,s')P(s')P(t \mid s) & \text{(使用规则三)} \end{alignat} }[/math]
应用案例2
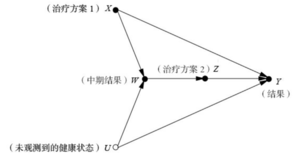
此案例由Nanny Wermuth和D. R. Cox给出[3],对应的实际例子可参见论文内容。其中治疗方案1(X)是随机施于患者的,而治疗方案2(Z)是根据治疗方案1所导致的中期结果(W)而制定的,在这里要计算的是干预两种治疗方案后对最终结果的因果效应,即[math]\displaystyle{ P(y \mid do(x), do(z)) }[/math]。可以再次使用Do演算将这个表达式转换为不包含Do算子的表达式。
[math]\displaystyle{ \begin{alignat}{3} P(y \mid do(x), do(z)) & = P(y \mid x, do(z)) & \text{(由于X是随机的)} \\ & = \Sigma_w P(y \mid x, w, do(z))P(w \mid x, do(z)) & \text{(使用规则一)} \\ & = \Sigma_w P(y \mid x, w, z)P(w \mid x, z) & \text{(使用规则二、三)} \end{alignat} }[/math]
相关算法
处理多变量干预算法
Jin Tian和Judea Pearl于2002年提出了第一个可以处理多变量被干预的算法[4]。
Identify算法
Identify算法由Yimin Huang和Marco Valtorta于2006年提出[5]。这个算法相较于上述Tian(2002)的算法消除了的对因果图的半马尔科夫性的限制,且也可以处理多变量干预的问题。
ID算法
ID算法由Ilya Shpitser和Judea Pearl与2006年提出[6],该算法的能力与上述Tian(2002)的算法等价,但更易于编程实现。
IDC算法
IDC算法由Ilya Shpitser和Judea Pearl与2006年提出[7],该算法是基于ID算法拓展的,可以处理联合干预条件分布的因果效应求解问题。
代码实现
Ananke
Ananke框架基于Python语言实现,集成了ID算法,详细内容可见Ananke开源地址
causaleffect
causaleffect框架基于R语言实现,集成了ID算法和IDC算法,详细内容可见causaleffect包信息地址
CEE
CEE框架基于Golang语言实现,集成了ID算法、IDC算法、Identify算法等,详细内容可见CEE开源地址
参考文献
- ↑ 1.0 1.1 Pearl, Judea (1995), "Causal diagrams for empirical research", Biometrika, 82 (4): 669–710, doi:10.1093/biomet/82.4.669.
- ↑ Huang, Yimin; Valtorta, Marco (2006). "Pearl's Calculus of Intervention is Complete". Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence: 217–224.
- ↑ Wermuth, Nanny; Cox, D. R. (2008). "Distortion of Effects Caused by Indirect Confounding". Biometrika. 95: 17–33.
- ↑ Tian, Jin; Pearl, Judea (2002). "A General Identification Condition for Causal Effects". Eighteenth National Conference on Artificial Intelligence: 567–573.
- ↑ Huang, Yimin; Valtorta, Marco (2006). "Identifiability in Causal Bayesian Networks: A Sound and Complete Algorithm". Proceedings of the 21st National Conference on Artificial Intelligence. 2: 1149–1154.
- ↑ Shpitser, Ilya; Pearl, Judea (2006). "Identification of Joint Interventional Distributions in Recursive Semi-Markovian Causal Models". Proceedings of the 21st National Conference on Artificial Intelligence. 2: 1219–1226.
- ↑ Shpitser, Ilya; Pearl, Judea (2006). "Identification of Conditional Interventional Distributions". Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence: 437–444.
编辑推荐
书籍推荐
这本书非常适合初学者入门因果科学,这里面涉及到对结构因果模型的详细定义和阐述,非常清晰易懂。
在本书中,人工智能领域的权威专家朱迪亚·珀尔及其同事领导的因果关系革命突破多年的迷雾,厘清了知识的本质,确立了因果关系研究在科学探索中的核心地位。
关于这本书集智俱乐部邀请白楚研究员用100分钟,为大家详细介绍了Judea Pearl绘制的因果科学蓝图,作为一个起点,去拥抱因果革命。可以查看对应的视频分享解读《为什么》:攀登因果之梯
课程推荐
- 这个视频内容来自集智俱乐部读书会-因果科学与Causal AI读书会第二季内容的分享,由英国剑桥大学及其学习组博士陆超超详细的阐述了潜在结果模型和结果因果模型,并介绍了两个框架的相互转化规律。
- 1. 讲述因果推断的两大框架:潜在结果模型和结构因果模型,讨论他们各自的优缺点以及他们之间的联系,详细介绍他们之间的转化规律。
- 2. 与大家一起深入探讨因果推断中最基本的概念、定理以及它们产生的缘由,了解每个概念背后的故事,从而建立起对因果更全面的感知。
- 3. 分享它们在不同学科中的具体的应用,包括社会科学、经济学、医学、机器学习等,借助这些应用,进一步启发大家用因果科学思维来思考和解决问题。
- 这个视频内容来自集智俱乐部读书会-因果科学与Causal AI读书会第一季内容的分享,这个视频为大家串讲因果推理的相关论文,着眼与因果研究的源头,简单介绍哲学中的因果思考。其次重点是用因果之梯(她的信息视角--回答因果问题需要相应的信息)和一个例子,来理解现代因果建模框架;最后梳理因果推理和 AI 领域的融合,以及Causal AI 的强人工智能之路。
文章总结
因果科学入门读什么书?Y. Bengio博士候选人的研读路径推荐
历时3个月,全球32位讲者,共同讲述因果科学与Causal AI的全景框架!
相关路径
- 因果科学与Casual AI读书会必读参考文献列表,这个是根据读书会中解读的论文,做的一个分类和筛选,方便大家梳理整个框架和内容。
- 因果推断方法概述,这个路径对因果在哲学方面的探讨,以及因果在机器学习方面应用的分析。
- 因果科学和 Causal AI入门路径,这条路径解释了因果科学是什么以及它的发展脉络。此路径将分为三个部分进行展开,第一部分是因果科学的基本定义及其哲学基础,第二部分是统计领域中的因果推断,第三个部分是机器学习中的因果(Causal AI)。
- 复杂网络动力学系统重构文献,这个路径是张江老师梳理了网络动力学重构问题,描述了动力学建模的常用方法和模型,并介绍了一些经典且重要的论文,这也是复杂系统自动建模读书会的主要论文来源,所以大部分都有解读视频。
- 因果纠缠集智年会——因果推荐系统分论坛关于因果推荐系统的参考文献和主要嘉宾介绍,来源是集智俱乐部的因果纠缠年会。
本中文词条由中科院计算所的李奉治博士贡献,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。
本词条由中科院计算所的李奉治博士生贡献。