基于有效信息的因果涌现理论
基于有效信息的因果涌现理论是该领域最早提出的一种用于定量刻画因果涌现强度的方法。该方法由Erik Hoel等人提出[1],其基本思想是将微观系统进行粗粒化后,使用一种因果效应度量指标有效信息来量化一个马尔科夫动力学的因果性强弱改变。如果粗粒化后的宏观系统的有效信息大于微观系统,那么就认为发生了因果涌现。
起源
2013年,Erik Hoel在文章[2]中首次使用有效信息指标,用来定量描述涌现现象,在有效信息指标的基础上提出了因果涌现理论。根据这一理论,一个马尔科夫动力系统中微观层次元素的状态转移规则,即因果机制是已知的,在此基础上,将多个微观元素或者元素状态进行合并,文中表述为粗粒化映射,可以得到宏观层次的系统。对比这两种情况可知,微观的因果机制是最完整的,宏观的所有因果机制都随附于微观机制产生。根据涌现现象,粗粒化后的宏观层次因果机制可以优于微观层次,作者提出有效信息这一指标度量系统因果机制的有效性。量化方式为将系统中的原因变量干预为均匀分布,然后计算原因变量和结果变量之间的互信息大小,即为Erik Hoel定义的有效信息,反映因果机制对原因和结果状态的约束强度,也就是因果相互作用强度。
2017年,Erik Hoel[3]引入信息论中香农定义的“信道容量”概念,提出系统中也存在类似“因果容量”。香农发现,信道上的信息传输速率对输入信号概率分布非常敏感,因此选择使系统输入输出互信息最大化的输入集合来定义信道容量,反映信道允许可靠传输信息的最大速率。类似地,在因果性度量中,根据定义,改变干预分布也会改变系统的有效信息,从微观映射到宏观层次的过程中实际改变了干预分布,因而发生因果性变化。除13年提出粗粒化用于改变干预分布之外,作者还提出设置部分变量为外生变量的方式,例如设置其一直保持初始状态,或允许其“黑盒”式在干预下变化但无法查看,可以组合使用这些方法以提升系统的因果性。因此,因果容量被定义为一个系统以最大信息量和最有效的方式将干预转化为结果的能力,Erik Hoel还提出一个普遍的原则:系统使用的改变干预分布方式越多,因果容量就越接近信道容量。
主要理论
马尔科夫动力系统
最初,基于有效信息的因果涌现理论是基于离散状态的马尔科夫动力学,即马尔科夫链展开定量化描述的。
马尔科夫链是指一种状态离散、时间离散的平稳随机过程,描述的是一组随机变量[math]X_t[/math]在状态空间[math]\mathcal{X}=\{1,2,\cdots,N\}[/math]上的取值,其中[math]t[/math]通常表示时间。其动力学一般可以用转移概率矩阵描述(Transitional Probability Matrix),简称TPM。该矩阵是一个概率矩阵,其中第[math]i[/math]行,第[math]j[/math]列元素[math]p_{ij}[/math],表示任意时刻[math]t[/math],系统在[math]i[/math]状态的条件下,下一时刻转移到[math]j[/math]状态的概率。因此,转移概率矩阵每一行均满足归一化条件:
[math]\displaystyle{ \sum_{j=1}^Np_{ij}=1, }[/math]
任意时刻[math]t+1[/math]上的状态概率分布,即[math]Pr(X_{t+1})[/math],可以被上一时刻的状态概率分布[math]Pr(X_t)[/math]和状态转移矩阵唯一确定,即满足:
[math]\displaystyle{ Pr(X_{t+1}=j)=\sum_{i=1}^N p_{ij}\cdot Pr(X_t=i), }[/math]
这里的[math]i,j\in \mathcal{X}[/math],是[math]\mathcal{X}[/math]中的任意状态,且[math]N=\#(\mathcal{X})[/math],即[math]\mathcal{X}[/math]中的总状态数。
量化方法
下面将引入有效信息这一关键指标,介绍如何基于该指标量化马尔科夫动力系统的因果效应。
有效信息
有效信息(Effective Information,简称EI)是因果涌现理论中的一个核心概念,它可以用来度量一个马尔科夫动力学的因果效应强度。
- EI定义
首先,我们先定义一般情况下的有效信息。因果效应度量的是系统动力学机制的有效性,即在给定动力学的情况下,因、果变量状态分布之间的关联程度(其中不能有混淆变量干扰)。由此可见,EI核心目标并非衡量是否存在因果效应,而是关注效应的强度,且更适用于已经明确存在因果关联的场合。更正式地,EI是因果机制的函数,而与其它因素无关,定义如下:
[math]\displaystyle{ EI(P)\equiv I(Y;X|do(X\sim U)) }[/math]
这里,[math]X[/math]是因变量,[math]Y[/math]是果变量,[math]P[/math]表示[math]X[/math]到[math]Y[/math]的因果机制。当[math]X, Y[/math]均为离散状态分布的情境下,[math]P[/math]为概率转移矩阵,[math]p_{ij}\equiv Pr(Y=j|X=i)[/math]。[math]do(X\sim U(\mathcal{X}))[/math]代表对[math]X[/math]实施do干预(或称do操作,英文是do-operator),使其服从[math]\mathcal{X}[/math]上的均匀分布[math]U(\mathcal{X})[/math],也即是最大熵分布。在这一干预下,因果机制P保持不变。EI指标度量的是经过do干预后的因变量X与果变量Y之间的互信息。
do干预这一步是根据Judea Pearl的因果阶梯理论[4]提出的。该理论中,因果推断包含了三个层次,分别是:关联、干预和反事实。阶梯层级越高,因果特征越明显。在EI的定义中引入了[math]do[/math]操作上升到干预层级,即设定变量为某个值或服从某个分布,使得EI能够比直接计算互信息更能体现因果特征。从实际意义上来讲,在EI的计算中引入do操作,可以把数据和动力学分开,消除数据分布(即[math]X[/math]的分布)对EI度量所带来的影响,均匀分布也避免了对数据分布的“偏见”。从因果图角度来看,do操作可以消除EI中的所有指向因变量[math]X[/math]的因果箭头,包括其它变量(包括不可观测的变量)对[math]X[/math]的影响,从而使得EI更能够刻画动力学本身的特性。
- 马尔科夫动力系统EI
回到离散状态的马尔科夫链中,任意时刻的状态变量[math]X_t[/math]可以看作是原因,而下一时刻的状态变量[math]X_{t+1}[/math]就可以看作是结果,马尔科夫链的状态转移矩阵就是它的因果机制。因此,马尔科夫链的有效信息定义如下:
[math]\displaystyle{ \begin{aligned} EI &= I(X_t,X_{t+1}|do(X_t\sim U(\mathcal{X})))=I(\tilde{X}_t,\tilde{X}_{t+1}) \\ &= \sum^N_{i=1}\sum^N_{j=1}Pr(\tilde{X}_t=i,\tilde{X}_{t+1}=j)\log \frac{Pr(\tilde{X}_t=i,\tilde{X}_{t+1}=j)}{Pr(\tilde{X}_t=i)Pr(\tilde{X}_{t+1}=j)}\\ &= \sum^N_{i=1}Pr(\tilde{X}_t=i)\sum^N_{j=1}Pr(\tilde{X}_{t+1}=j|\tilde{X}_t=i)\log \frac{Pr(\tilde{X}_{t+1}=j|\tilde{X}_t=i)}{Pr(\tilde{X}_{t+1}=j)}\\ &= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{N\cdot p_{ij}}{\sum_{k=1}^N p_{kj}} \end{aligned} }[/math]
同理,其中[math]\displaystyle{ \tilde{X}_t,\tilde{X}_{t+1} }[/math]分别为把[math]X_t[/math]干预为均匀分布后,[math]t[/math]时刻与下一时刻的状态。[math]\displaystyle{ p_{ij} }[/math]为第i个状态转移到第j个状态的转移概率,N为总状态数。从这个式子,不难看出,EI仅仅是概率转移矩阵[math]P[/math]的函数。
进一步,为方便计算,我们也可以将转移概率矩阵[math]P[/math]写成[math]N[/math]个行向量拼接而成的形式,即:
[math]\displaystyle{ P=(P_1^T,P_2^T,\cdots,P_N^T)^T }[/math]
其中,[math]P_i[/math]矩阵[math]P[/math]的第[math]i[/math]个行向量,且满足条件概率的归一化条件:[math]||P_i||_1=1[/math],这里的[math]||\cdot||_1[/math]表示向量的1范数。那么EI可以进一步写成如下的形式:
-
[math]\displaystyle{ \begin{aligned} EI &= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{N\cdot p_{ij}}{\sum_{k=1}^N p_{kj}}\\ &=\frac{1}{N}\cdot \sum_{i=1}^N\left(P_i\cdot \log P_i - P_i\cdot\log \bar{P}\right)\\ &=\frac{1}{N}\sum_{i=1}^N D_{KL}(P_i||\bar{P}) \end{aligned} }[/math]
(2)
将矩阵每列求均值,可得到平均转移向量[math]\displaystyle{ \overline{P}=\sum_{k=1}^N P_k/N }[/math]。因此,EI是概率转移矩阵每个行转移向量[math]P_i[/math]与平均转移向量[math]\bar{P}[/math]的KL散度的均值。
- EI分解
在行向量形式表示的马尔科夫链中,EI可以进一步拆解:
-
[math]\displaystyle{ \begin{aligned} EI &=\frac{1}{N}\sum_{i=1}^N D_{KL}(P_i||\bar{P}) \\ &= \frac{1}{N}\cdot \sum_{i=1}^N\left(P_i\cdot \log P_i - P_i\cdot\log \bar{P}\right)\\ &=\underbrace{-\langle H(P_i)\rangle}_{确定性项}+\underbrace{H(\bar{P})}_{非简并性项} \end{aligned} }[/math]
(tow_terms)
其中,第一项:[math]-\langle H(P_i)\rangle\equiv -\frac{1}{N}\sum_{i=1}^N H(P_i)[/math]为每个行向量[math]P_i[/math]的负熵的平均值,它刻画了整个马尔科夫转移矩阵的确定性(determinism),即在动力学的作用下,可以在多大程度上根据系统前一时刻的状态预测它下一时刻状态。确定性高对应,很大程度可以成功预测下一状态。
第二项:[math]H(\bar{P})[/math]为平均行向量的熵,其中[math]\bar{P}\equiv \frac{1}{N}\sum_{i=1}^N P_i [/math]为所有N个行向量的平均行向量,它刻画了整个马尔科夫转移矩阵的非简并性或非退化性(non-degeneracy),即在动力学的作用下,能够以多大程度从下一时刻的状态推断上一时刻的状态。非简并性高对应,很大程度可以正确推断上一时刻状态。
- 确定性与简并性
然而,上述定义中的确定性项和非简并性都是负数,为此,我们重新定义一个马尔科夫链转移矩阵P的确定性为:
[math]\displaystyle{ Determinism \equiv \log N - \langle H(P_i)\rangle = \frac{1}{N}\sum_{i=1}^N \sum_{j=1}^N p_{ij}\log \left(N\cdot p_{ij}\right) }[/math]
这一项是一个平均的负熵,为了防止其为负数,所以加上了[math]\log N[/math][5]。Determinism能刻画整个转移矩阵的确定性:也就是说如果我们知道了系统当前时刻所处的状态,则我们能够推断出系统在下一时刻所处的状态的程度。为什么这么说呢?这是因为确定性这一项是所有行向量熵的平均值,再取一个负号。我们知道,当一个向量更靠近均匀分布的时候,它的熵就越大,相反,如果一个向量越靠近一个“独热”(one-hot)的向量,也就是这个向量中只有一个1,其它元素都是0,那么它的熵就越小。我们知道,马尔科夫概率转移矩阵的一个行向量的含义就代表系统从当前状态转移到各个不同状态的概率大小。那么,当平均的行向量负熵大的时候,也就是这个行向量的某一个单元概率为1,其它为0,这就意味着系统能够确定地转移到1对应的状态。
我们定义一个马尔科夫链转移矩阵P的简并性为:
[math]\displaystyle{ Degeneracy \equiv \log N - H(\bar{P})=\log N + \sum_{j=1}^N \bar{P}_{\cdot j}\log \bar{P}_{\cdot j}=\sum_{j=1}^N \frac{\sum_{i=1}^Np_{ij}}{N}\log \left(\sum_{i=1}^Np_{ij}\right) }[/math]
这一项为简并性或叫退化性,为了防止其为负数,所以也加上了[math]\log N[/math][6]。这里的“简并性”的含义是:如果知道了系统的当前状态,能不能反推系统在上一时刻的状态的能力,如果可以推断,则这个马尔科夫矩阵的简并性就会比较低,也就是非简并的;而如果很难推断,则马尔科夫矩阵就是简并的,也即退化的。为什么“简并性”可以用平均行向量分布的负熵来刻画呢?这是因为,首先,当所有的P中的行向量都是彼此独立的独热向量,那么它们的平均分布就会非常接近于一个均匀分布,即[math]\bar{P}\approx (\frac{1}{N},\frac{1}{N},\cdots,\frac{1}{N})[/math],这个时候,它的Shannon熵最大,即[math]\log N[/math]。而在此时,这个马尔科夫转移矩阵是一个可逆矩阵(由彼此独立的“独热”向量形成的全体彼此线性无关,因此矩阵满秩,因此是可逆的)。这也就意味着,我们从系统当前的状态,是可以推断出系统的上一时刻的状态的,所以这个马尔科夫转移矩阵是非简并的,计算出的简并度恰恰也为0;
其次,当P中的行向量都是相同的独热向量的时候,则平均向量也是一个独热的向量,而这种向量的熵是最小的。在此时,由于所有的上一时刻状态都会转移到行向量中1对应的状态,因此我们也就很难推断出当前这个状态是由哪一个上一步的状态转移过来的。因此,这种情形下的马尔科夫矩阵是简并的(或退化的),计算出来的简并度则恰恰是[math]\log N[/math]。
对于更一般的情况,如果P中的行向量靠近一个彼此独立的独热行向量构成的矩阵,则P就越非简并,相反,如果行向量彼此相同且靠近同一个独热向量,则P就越简并。
因此,有效信息通常可以分解为两个部分:[math]\displaystyle{ EI=Det-Deg }[/math],Det是确定性(Determinism)的缩写,Deg是简并性(Degeneracy)的缩写。因此,如果一个转移矩阵具有较高的确定性和较低的简并性,则它的EI就会很高。
- EI归一化
显然,EI的大小和状态空间大小有关,这一性质在我们比较不同尺度的马尔科夫链的时候非常不方便,我们需要一个尽可能不受尺度效应影响的因果效应度量。因此,我们需要对有效信息EI做一个归一化处理,得到和系统尺寸无关的一个量化指标。
根据Erik Hoel和Tononi等人的工作,要用均匀分布即最大熵分布下的熵值,即[math]\displaystyle{ \log N }[/math]来做分母对EI进行归一化,这里的[math]N[/math]为状态空间[math]\mathcal{X}[/math]中的状态的数量。那么归一化后的EI便等于:
[math]\displaystyle{ Eff=\frac{EI}{\log N} }[/math]
进一步定义归一化指标也称为有效性(effectiveness)。
然而,在处理连续状态变量的时候,这种使用状态空间中状态数量的对数值进行归一化的处理方式并不是非常合适,因为这一状态数往往受到变量的维度和实数分辨率的影响。
- 计算实例
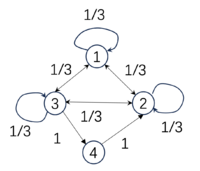
下面,给出三个马尔科夫链的例子,以及相应的EI数值也放到了下面:
|
[math]\displaystyle{ P_1=\begin{pmatrix} &0 &0 &1 &0& \\ &1 &0 &0 &0& \\ &0 &0 &0 &1& \\ &0 &1 &0 &0& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_2=\begin{pmatrix} &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &0 &0 &0 &1& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_3=\begin{pmatrix} &0 &0 &1 &0& \\ &1 &0 &0 &0& \\ &1 &0 &0 &0& \\ &1 &0 &0 &0& \\ \end{pmatrix} }[/math]. |
| [math]\begin{aligned}&EI(P_1)=2\ bits,\\&Det(P_1)=2\ bits,\\&Deg(P_1)=0\ bits\end{aligned}[/math] | [math]\begin{aligned}&EI(P_2)=0.81\ bits,\\&Det(P_2)=0.81\ bits,\\&Deg(P_2)=0\ bits\end{aligned}[/math] | [math]\begin{aligned}&EI(P_3)=0.81\ bits\\&Det(P_3)=2\ bits,\\&Deg(P_3)=1.19\ bits.\end{aligned}[/math] |
-
(example)
我们可以看到,第一个转移概率矩阵是一个排列矩阵(Permutation),因此该矩阵可逆。它是一个完全确定性的转移,即从任意状态出发,下一时刻会以100%的概率转移到另外某一个状态;也是完全非简并的,从下一时刻可以100%回推得到上一时刻的状态。因此确定性最高,没有简并性,EI最大;
第二个矩阵的前三个状态都会以1/3的概率跳转到彼此,因此确定性程度最低,而简并性也很低,EI是0.81;
第三个矩阵虽然也是非0即1的转移概率,因而确定性最高,但是由于后三个状态都跳转到1,因此,从1状态不能推知它来自于哪个状态,因此简并性最高,最终的EI与第二个相同,仍然是0.81。
粗粒化映射
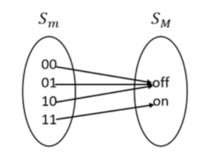
微观元素状态空间[math]S_m[/math]通过映射[math]M: S_m \rightarrow S_M[/math]映射到宏观元素状态空间[math]S_M[/math],映射方法可以针对微观元素的空间或(和)时间维度。空间映射的对象是不同微观元素状态,时间映射针对的是同一微观元素不同时间步的状态。要求粗粒化映射对微观元素而言,必须是穷尽(exhaustive)和互斥的(disjunctive),即一个微观元素的所有状态必须映射到同一个宏观元素的各种状态。粗粒化映射会带来系统的状态空间减小,但也允许宏观元素可以由单个微观元素组成。
以布尔元素为例,两个微观元素共有四种状态[math]S_m = \{00,01,10,11\}[/math],按照[math]M:[[00,01,10] = off, [11] = on][/math]的映射规则,可以得到宏观尺度一个元素的两种状态,即[math]S_M = \{on, off\}[/math]。
关于如何对马尔科夫概率转移矩阵实施粗粒化的方法,往往体现为两步:1、对微观状态做归并,将N个微观态,归并为M个宏观态;2、对马尔科夫转移矩阵做约简。关于具体的粗粒化马尔科夫链的方法,请参考马尔科夫链的粗粒化。
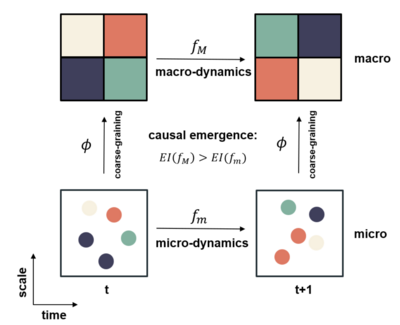
因果涌现度量
基于有效信息的定义,结合对系统粗粒化的操作,我们可以量化系统粗粒化后因果效应的变化,即度量因果涌现。下面给出了因果涌现框架的示意图。其中,横坐标表示时间(time),纵坐标表示尺度(scale)。该框架可以看成是对同一个动力系统在微观和宏观两种尺度上的描述。其中,[math]f_m[/math]表示微观动力学,[math]f_M[/math]表示宏观动力学,二者通过一个粗粒化函数[math]\phi[/math]相连。在一个离散状态的马尔科夫动力系统中,[math]f_m[/math]和[math]f_M[/math]都是马尔科夫链,对[math]f_m[/math]进行马尔科夫链的粗粒化,就可以得到[math]f_M[/math]。[math]\displaystyle{ EI }[/math]是有效信息的度量。由于微观态可能具有更大的随机性,这导致微观动力学的因果性比较弱,所以通过对每一个时刻的微观态进行合理的粗粒化,就有可能得到因果性更强的宏观态。所谓的因果涌现,就是指当我们对微观态进行粗粒化的时候,宏观动力学的有效信息会增加这一现象,并且宏观态与微观态的有效信息之差被定义为因果涌现的强度。
因果涌现指标CE的定义为:
[math]\displaystyle{ CE = EI(P') - EI(P) }[/math]
这里[math]P[/math]为微观状态的马尔科夫概率转移矩阵,维度为:[math]N\times N[/math],这里N为微观的状态数;而[math]P'[/math]为对[math]P[/math]做粗粒化操作之后得到的宏观态的马尔科夫概率转移矩阵,维度为[math]M\times M[/math],其中[math]M<N[/math]为宏观状态数。
如果计算得出的CE>0,则称该系统发生了因果涌现,否则没有发生。有时,我们也会根据归一化的EI来计算因果涌现度量,即:
[math]\displaystyle{ ce=Eff(P_M)-Eff(P_m) }[/math]
由于归一化的EI消除了系统尺寸的影响,因此这种方式得到的因果涌现度量值更大。
状态空间的因果涌现
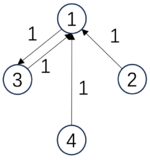
一个简单的基于状态空间因果涌现实例如下:一条离散的马尔科夫链[math]S_m[/math],共有4个可能的状态,状态转移概率矩阵[math]P_m[/math]如下所示:
|
[math]\displaystyle{ P_m=\begin{pmatrix} &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &0 &0 &0 &1& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_M=\begin{pmatrix} &1 &0 & \\ &0 &1 & \\ \end{pmatrix} }[/math]. |
| [math]\begin{aligned}&Det(P_m)=0.81\ bits,\\&Deg(P_m)=0\ bits,\\&EI(P_m)=0.81\ bits\end{aligned}[/math] | [math]\begin{aligned}&Det(P_M)=1\ bits,\\&Deg(P_M)=0\ bits,\\&EI(P_M)=1\ bits\end{aligned}[/math] |
在这个例子中,微观态的转移矩阵[math]P_m[/math]是一个4*4的矩阵,其中前三个状态彼此以1/3的概率相互转移,这导致该转移矩阵具有较小的确定性,因此EI也不是很大为0.81。然而,当我们对该矩阵进行粗粒化,也就是把前三个状态合并为一个状态a,而最后一个状态转变为一个宏观态b。这样所有的原本三个微观态彼此之间的转移就变成了宏观态a到a内部的转移了。因此,转移概率矩阵也就变成了[math]P_M[/math],它的EI为1。在这个例子中,可以计算它的因果涌现度量为:
[math]\displaystyle{ CE=EI(P_M)-EI(P_m)=1-0.81=0.19\ bits }[/math]
[math]\displaystyle{ ce=Eff(P_M)-Eff(P_m)=1-0.405=0.595 }[/math]
即存在着0.19比特的因果涌现,或用有效性度量得到0.595的因果涌现。
变量角度的因果涌现
下面从变量角度,分别给出了空间、时间和时空因果涌现的布尔网络实例,从微观系统机制、粗粒化映射和宏观尺度分析三个方面进行描述和分析。注:[math]S_m[/math]表示微观系统;[math]S_M[/math]表示粗粒化得到的宏观系统。微观元素是布尔值且用拉丁字母[math]\{A, B, C…\}[/math]标记,宏观元素用希腊字母[math]\{α, β, γ. .\}[/math]标记。微观状态标记为[math]\{1,0\}[/math],宏观状态标记为{“on”,“off”,“bursting”,“quiet”…}。
空间因果涌现
根据前文,因果涌现量化指标可以拆分为确定性和简并性两项。接下来,分别对由确定性和简并性主导的因果涌现给出一个实例,介绍空间因果涌现。
1.提高确定性实例分析
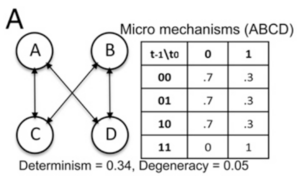
微观尺度:微观系统由四个布尔元素组成[math]S_m = \{ABCD\}[/math] (图A),其中A和B一组,C和D一组,其中一个组中的每个元素[math]t+1[/math]时刻的状态由另一组两个元素[math]t[/math]时刻的状态决定。机制是一个带噪声的AND门,图A右侧为详细的对应关系。举例来看,假设[math]t[/math]时刻CD = {00},则[math]t+1[/math]时刻,A和B每个元素有0.7的概率为0,0.3的概率为1,AB组水平的状态总共可能有以下四种:{00},{01},{10},{11},每种组状态概率由组成元素单独的状态概率相乘得到,所以分别对应为0.49,0.21,0.21,0.09,满足概率之和为1。考虑到每个元素都有两个可能状态,则系统总共有[math]2^4=16[/math]个可能的状态,将系统以等概率设置为所有可能的微观状态,可以计算得到一个16 × 16 [math]S_m[/math] 的概率转移矩阵(图C),计算可以按照上面举例的组水平状态集合间的转移概率来算。再根据EI的公式可以计算得到有效信息[math]EI(S_m) = Det(S_m) - Deg(S_m) = 1.35 - 0.20 = 1.15 \text{ bits}[/math],[math]Eff(S_m) = EI(S_m)/ \log N = 1.15/4 = 0.29[/math]。
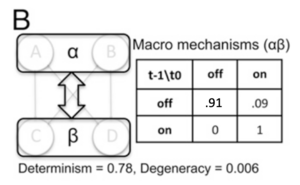
粗粒化映射:从图C可以看出,这个概率转移矩阵非常复杂,但同时矩阵也有一些规律可循,比如前12行和后4行的模式差异较大,前12行中每4行的模式都是重复的。因此思考是否可以提炼出其中的规律,更加高效地表达系统间的状态转移模式。首先可以看系统内是有分组机制,四个元素被分为了两组,每组都接受另一组元素的输入且响应机制相同,同组元素的状态之间不会互相影响,因此同组元素之间是独立等价的,可以被映射或归类为同一个宏观元素。微观系统[math]S_m = \{ABCD\}[/math]可以被粗粒化为有两个元素[math]{α, β}[/math]的宏观系统[math]S_M[/math]。考虑微观状态的转移机制(图A右侧),输入值00,01和10决定状态的规则相同,输入值11对应另一种,因此每个宏观元素状态可以映射为{"off" ,"on"}两种(图D)。
宏观尺度:宏观系统现在由2个元素组成,每个元素由2个状态,所以宏观系统整体共有[math]2^2=4[/math]个可能的状态。将系统以等概率设置为所有可能的宏观状态,根据宏观的转移规则,可以得到 4 × 4 的[math]S_M[/math] 概率转移矩阵(图E)。由图E可见,矩阵规模减小,但是状态间的转移规律更明确。宏观尺度下[math]EI(S_M) = Det(S_M) - Deg(S_M) = 1.56 - 0.01 = 1.55 \text{ bits}[/math],[math]Eff(S_M) = 0.78[/math],高于微观尺度的[math]EI(S_m) = 1.15 \text{ bits}[/math]。因此,因果涌现度量[math]CE(S) = EI(S_M) - EI(S_m) = 0.40 \text{ bits}[/math],宏观的因果性优于微观,因果涌现发生。
本例中,在宏观尺度的有效性[math]\Delta I_{Eff}[/math]的增益主要来自于减少噪声干扰,即确定性提高(归一化后:[math]Det(S_m) = 0.34[/math]; [math]Det(S_M) = 0.78[/math]),少部分来源于简并性减少(归一化后:[math]Deg(S_m) = 0.05[/math]; [math]Deg(S_M) = 0.006[/math])。
2.抵消简并性实例分析
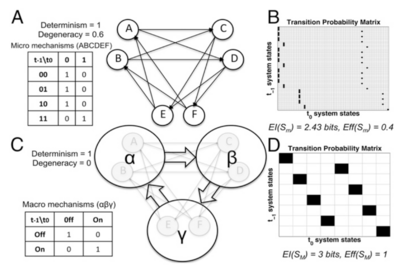
微观机制:微观系统由6个布尔元素[math]S_m = \{ABCDEF\}[/math]构成,其中A、B接受E和F的输入,C、D接受A和B的输入,E、F接受C和D输入。连接机制为确定性AND门,对应完全确定性和高简并度(图A)。微观系统的概率转移矩阵如图B所示,可以得到[math]EI(S_m) = 2.43 \text{ bits}[/math],[math]Eff(S_m) = 0.4[/math](图B)。
粗粒化映射:同上例,根据微观机制的分组,接受相同输入的元素可以被分为同一组,因此可以分为3个宏观元素。根据机制的同类性,{[00,01,10], [11]}可分别对应宏观态{"off" ,"on"},确定性AND门映射为COPY门,即宏观元素完全复制输入元素的状态(图C左侧)。最优粗粒化方案即为将6个微观AND门映射为3个宏观COPY门(图C的αβγ)。
宏观尺度:宏观尺度的概率转移矩阵如图D所示,可得到宏观[math]EI(S_M) = 3 \text{ bits}[/math],[math]Eff(S_M) = 1[/math],[math]CE = EI(S_M) - EI(S_m) = 0.57 \text{ bits}[/math],因果涌现发生。进一步拆解分析可知,微观和宏观机制都是完全确定性的,但粗粒化后宏观简并性明显减小 [math]\Delta Deg = -0.6[/math],即在本实例中粗粒化映射抵消简并性主导了因果涌现的发生。
时间因果涌现
对时间变量进行粗粒化映射也会有涌现现象发生,具体形式为:将微观时间步([math]t_x[/math]) 粗粒化为宏观时间步([math]T_x[/math])。下面对一个时间因果涌现实例进行分析:
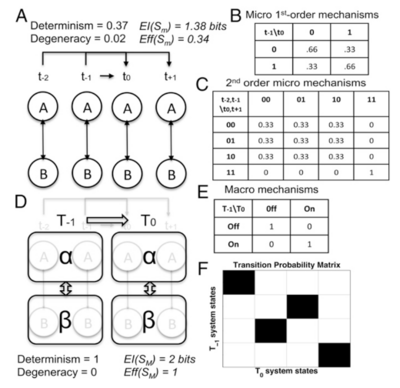
微观机制:微观系统有A和B两个元素,元素[math]t[/math]和[math]t+1[/math]的状态由另一元素[math]t-2[/math]和[math]t-1[/math]时刻的状态决定,即遵循二阶马尔可夫机制(图A)。具体的状态决定机制如图C所示,当B前两时刻([math]t-2[/math],[math]t-1[/math])状态为{11}时,A当前和后一时刻([math]t[/math],[math]t+1[/math])状态可确定为{11};当B前两时刻状态为其余三种情况{00,01,10},A当前和后一时刻状态会以等概率出现这三种情况中的一种。基于一个微观时间步分析(图B),得到 [[math]EI(S_m) = 0.16 \text{ bits}[/math];[math]Eff(S_m) = 0.03[/math]],因果相互作用较弱,因为忽略了系统二阶性质。开展两个微观时间步的因果分析(图C),可以得到 [math]EI(S_m) = 1.38 \text{ bits}[/math],[math]Eff(S_m) = 0.34[/math]。
粗粒化映射:根据二阶马尔科夫性质,将微观状态的时间步分组为宏观状态[math]α = {A_t, A_{t+1}}[/math]和[math]β = {B_t, B_{t+1}}[/math](图D);同空间因果涌现实例,图C概率转移矩阵中状态间明显的界限,可以将{[00,01,10],[11]}分别映射为{"off","on"}两个宏观状态。
宏观尺度:时间步粗粒化后得到的宏观机制如图E所示,此时机制为完全确定和非简并的,即宏观时间尺度下 [math]EI(S_M) = 2 \text{ bits}[/math],[math]Eff(S_M) = 1[/math], [math]CE(S) = EI(S_M) - EI(S_m) = 0.62 \text{ bits}[/math],因果涌现发生。
时空因果涌现
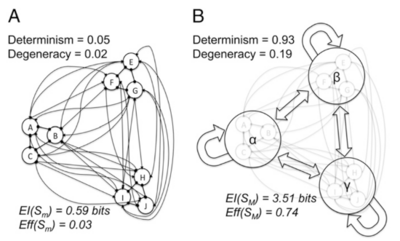
因果涌现现象还可以基于对空间、时间同时进行粗粒化产生,下面对图中实例进行具体分析:
微观机制:
- 时间机制:所有微观元素也遵循二阶马尔可夫机制,整合前两个时间步([math]t_{-2}[/math], [math]t_{-1}[/math])的输入,决定后两个时间步([math]t_0[/math], [math]t_{+1}[/math])的状态。所有微观元素自发活动(0/1),1为发放状态,每个元素具有非均匀的发放概率:[math]p(A/D/G) = 0.45[/math];[math]p(B/E/H) = 0.5[/math];[math]p(C/F/I) = 0.55[/math]。
- 组机制:所有元素被划分为三组[math]{ABC, DEF, GHI}[/math],每个元素都接收组内和组间元素的输入,图中分别以圆箭头和常规箭头表示。在每组内,如果两个时间步内组内输入之和[math]\sum(intra) = 0[/math],接下来的两个时间步所有元素保持为0。然而,如果在两个时间步中,与另外两组中的元素输入之和[math]\sum(inter) = 6[/math],则在接下来的两个时间步中,发放概率提高0.5。
微观尺度下,系统机制的 [math]EI(S_m) = 0.59 \text{ bits}[/math]; [math]Eff(S_m) = 0.033[/math]。
粗粒化映射:根据组机制,三组神经元在空间上映射为三个宏观成分,对应空间粗粒化映射;根据二阶马尔科夫性质,将两个微观时间步长整合为一个宏观时间步长,对应时间粗粒化映射(图B)。
宏观尺度:时空粗粒化后的系统具有比微观更高的[math]EI(S_M) = 3.51 \text{ bits}[/math],和[math]Eff(S_M) = 0.74[/math],[math]CE(S) = 2.92 \text{ bits}[/math],因果涌现发生。粗粒化过后系统确定性的增加,增加程度远超过简并性的增加。
注:本实例可对应真实神经元活动上的解释。宏观层面可理解为神经元“微柱”(minicolumn)的三种状态:“抑制态”(“微柱中神经元均在Tx时静默),“感受态”(部分在Tx时放电)和“爆发态”(所有均在Tx处放电)。宏观的因果相互作用可以解释为,如果一个宏观成分处于抑制态,那么只有接收到一次其他微柱的发放才能转换到“感受态”,以及不太可能的“爆发态”;否则,它将一直保持抑制态。
代码
这里提供了基于有效信息计算的因果涌现的python代码,以供参考:https://github.com/KellyPPeng/effective-information-calculation
代码包括两部分:第一部分上述实例的实现,即给定微观机制和粗粒化方案,分别在状态空间和变量空间计算因果涌现;第二部分是参考https://github.com/jkbren/einet,提供的使用贪婪算法和谱分解方法,在微观转移概率矩阵中学出最优粗粒化方案,算法实现步骤拆解可参考复杂网络中的因果涌现。
应用
- 复杂网络
2020年,Klein和Hoel改进马尔科夫链上定量化因果涌现的方法以应用到复杂网络中[7],作者借助随机游走子来定义网络中的马尔科夫链,将随机游走子放在节点上等价于对节点做干预,然后基于随机游走概率定义节点间的转移概率矩阵。同时作者将有效信息与网络的连通性建立联系,连通性可以通过节点的出边和入边的权重的不确定性来表征,基于此定义复杂网络中的有效信息。详细方法可以参考复杂网络中的因果涌现。
作者在随机网络(ER)、偏好依附网络模型(PA)等人工网络以及四类真实网络中进行了实验比较,发现:对于ER网络来说,有效信息的大小只依赖于连接概率[math]\displaystyle{ p }[/math],并且随着网络规模的增大会收敛到数值[math]\displaystyle{ -\log_2p }[/math]。同时一个关键发现表明,EI数值存在一个相变点,该相变点近似在网络的平均度([math]\displaystyle{ \lt k\gt }[/math])等于[math]\displaystyle{ \log_2N }[/math]的位置出现,同样对应于ER网络随着连接概率增加而出现巨连通集团的相变点位置,超过该相变点随机网络结构不会随着其规模的增加而包含更多的信息。对于偏好依附模型网络来说,当网络度分布的幂律指数[math]\displaystyle{ \alpha\lt 1.0 }[/math]时,有效信息的大小会随着网络规模的增加而增大;当[math]\displaystyle{ \alpha\gt 1.0 }[/math]时,结论相反;[math]\displaystyle{ \alpha=1.0 }[/math]刚好对应的无标度网络则是增长的临界边界。对于真实网络来说,作者们发现,生物网络因为具有很大的噪音,所以有效信息最低。然而,我们可以通过有效的粗粒化去除这些噪音,这就使得生物网络相比于其他类型网络能够展现出更显著的因果涌现现象;而因为技术类型网络是更稀疏、非退化,因此,平均效率更高,节点关系也更加具体,所有有效信息也最高,但是难以通过粗粒化来增加因果涌现度量。
在该文章中,作者使用贪婪算法来粗粒化网络,然而对于大规模网络来说,这种算法效率很低。随后,Griebenow等[8]提出了一种基于谱聚类的方法来识别偏好依附网络中的因果涌现。相比贪婪算法以及梯度下降算法,谱聚类算法的计算时间更少,同时找到的宏观网络的因果涌现也更加显著。
- 生物系统
进一步,Klein等人将复杂网络中的因果涌现方法扩展到了更多的生物网络中。前文已经指出,生物网络具有更大的噪音,这使得我们很难理解其内部的运作原理,这种噪音一方面来自系统的固有噪音,另一方面是由于测量或观察引入的。Klein等[9]进一步探索了生物网络中的噪声、简并性和确定性三者之间的关系以及具体含义,得出了一些有趣的结论。
例如,基因表达网络中的高确定性可以理解为一个基因几乎肯定会导致另一个基因的表达。同时生物系统在进化过程中也普遍存在高简并性现象。这两个因素共同导致,目前人们尚不清楚应该在何种尺度上分析生物系统才能更好理解它们的功能。Klein等[10]分析了超过1800个物种的蛋白质相互作用网络,发现宏观尺度的网络具有更小的噪音和简并性,同时与不参与宏观尺度的节点相比,组成宏观尺度网络中的节点更具有弹性。因此,生物网络为了适应进化的要求,需要演化出宏观尺度以提高确定性来增强网络弹性以及提高信息传输的有效性。
Hoel等在文章[11]中借助有效信息理论进一步研究了生物系统中的因果涌现。作者将有效信息应用到基因调控网络上,以识别最能提供信息的心脏发育模型从而控制哺乳动物的心脏发育。通过量化酿酒酵母基因网络的最大连通集团中的因果涌现,文章揭示了富有信息的宏观尺度在生物学中是普遍存在的,以及生命机制本身也经常运行在宏观尺度上。该文章也为生物学家提供了一种可计算的工具来识别最具有信息的宏观尺度,并且可以在此基础上建模、预测、控制和理解复杂的生物系统。
Swain等在文章[12]中探索了蚁群的交互历史对任务分配和任务切换的影响,使用有效信息研究噪声如何在蚂蚁之间传播。结果发现,蚁群之间历史交互程度影响任务的分配,并且具体交互中蚂蚁群体的类型决定了交互中的噪音。此外,即使当蚂蚁切换功能群时,蚁群涌现出来的凝聚力也能保证群体的稳定,同时不同功能蚁群在维持蚁群凝聚力方面也发挥着不同的作用。
缺陷与争议
- 依赖粗粒化策略
根据上述实例可以发现,得到宏观动力学的有效信息,需要基于给定的粗粒化策略。在状态、变量较少,且转移概率矩阵有明显的规律可循时,可以相对容易定义粗粒化策略并识别因果涌现。但对于情况复杂的实际系统时,例如生物系统,通常需要穷尽所有粗粒化方案得到最大宏观有效信息,相应的计算复杂度极高,适用性不强。
为了避免对粗粒化策略的依赖,Rosas等人引入了一种新的不依赖于粗粒化方法的因果涌现的定量定义,即为基于信息分解的因果涌现理论。该定义借鉴了部分信息分解理论(PID),旨在将目标变量和源变量之间的互信息分解为不重叠的三种信息原子:特有信息、冗余信息和协同信息。在此基础上,Rosas进一步发展了这一概念,并引入了称为φlD的理论来分解多个目标变量和源变量之间的互信息。该框架基于系统的协同信息来定量刻画涌现,通过测量源变量和目标变量之间的协同信息,如果协同信息值大于零,即可判定发生了因果涌现。
参考文献
- ↑ Hoel, E.P., Albantakis, L. and Tononi, G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49), 19790-19795.
- ↑ Hoel, E.P., Albantakis, L. and Tononi, G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49), 19790-19795.
- ↑ Hoel, E.P. When the map is better than the territory[J]. Entropy, 2017, 19(5), p.188.
- ↑ Judea Pearl; 刘礼; 杨矫云; 廖军; 李廉 (4 2022). 因果论——模型、推理和推断. 机械工业出版社.
- ↑ Hoel, E.P., Albantakis, L. and Tononi, G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49), 19790-19795.
- ↑ Hoel, E.P., Albantakis, L. and Tononi, G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49), 19790-19795.
- ↑ Klein B, Hoel E. The emergence of informative higher scales in complex networks[J]. Complexity, 2020, 20201-12.
- ↑ Griebenow R, Klein B, Hoel E. Finding the right scale of a network: efficient identification of causal emergence through spectral clustering[J]. arXiv preprint arXiv:190807565, 2019.
- ↑ Klein B, Swain A, Byrum T, et al. Exploring noise, degeneracy and determinism in biological networks with the einet package[J]. Methods in Ecology and Evolution, 2022, 13(4): 799-804.
- ↑ Klein B, Hoel E, Swain A, et al. Evolution and emergence: higher order information structure in protein interactomes across the tree of life[J]. Integrative Biology, 2021, 13(12): 283-294.
- ↑ Hoel E, Levin M. Emergence of informative higher scales in biological systems: a computational toolkit for optimal prediction and control[J]. Communicative & Integrative Biology, 2020, 13(1): 108-118.
- ↑ Swain A, Williams S D, Di Felice L J, et al. Interactions and information: exploring task allocation in ant colonies using network analysis[J]. Animal Behaviour, 2022, 18969-81.
编者推荐
下面是一些链接能够帮助读者更好的了解基于有效信息的因果涌现理论的相关信息:
因果涌现读书会
文章推荐
- Hoel, E.P., Albantakis, L. and Tononi, G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49), 19790-19795.
- Hoel, E.P. When the map is better than the territory[J]. Entropy, 2017, 19(5), p.188
路径推荐
- 张江老师根据因果涌现读书会第一季梳理的关于因果涌现的学习路径:https://pattern.swarma.org/article/153
- 张江老师根据因果涌现前五季读书会整理的因果涌现入门路径:https://pattern.swarma.org/article/296
此词条由彭晨编写,xx整理和审校。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。