Lotka–Volterra方程式
Lotka–Volterra方程式(洛特卡-沃尔泰拉方程式,又称为捕食者-猎物方程 predator–prey equations,以下简称为捕猎方程 predator)是一对一阶非线性微分方程组,我们经常用它来描述两个物种间因捕食和被捕食关系而形成的动力学系统,这样的系统可称为捕猎系统。该方程组反映了此二者物种的种群数量会随时间变化并遵循如下规律:
- [math]\displaystyle{ \begin{align} \frac{dx}{dt} &= \alpha x - \beta x y, \\ \frac{dy}{dt} &= \delta x y - \gamma y, \end{align} }[/math]
其中:
- x是猎物(例如兔子)的数量;
- y是捕食者(例如狐狸)的数量;
- [math]\displaystyle{ \tfrac{dy}{dt} }[/math] 和 [math]\displaystyle{ \tfrac{dx}{dt} }[/math]代表这两个种群的瞬时增长率;
- t代表时间;
- α, β, γ, δ是描述两个物种相互作用的正实参数。
Lotka–Volterra方程组是Kolmogorov模型(柯尔莫戈洛夫模型)的一个示例,而Kolmogorov模型[1][2][3]具有更一般的模型框架,可以用来刻画捕食者与猎物之间因猎食,竞争,疾病和共生等关系而形成的生态动力系统。
历史
Lotka–Volterra捕猎模型最初是由Alfred J. Lotka于1910年在自催化化学反应理论中提出的[4][5]。这个模型实际上是一类逻辑方程[6] ,源自于Pierre François Verhulst[7] 。1920年,Lotka以植食和草食性动物为例[8],在Andrey Kolmogorov的帮助下将该模型扩展到了“有机系统”,并于1925年,他在自己编写的生物数学书中使用了这些方程式分析了捕食者与猎物之间的相互关系[9]。1926年,数学和物理学家Vito Volterra发表了同样的方程组。沃尔泰拉对数理生物学非常感兴趣[5][10][11],他对该领域的研究受到了与海洋生物学家Umberto D'Ancona交流的启发,当时D'Ancona正向他的女儿求婚,不久后便成了他的女婿。D'Ancona研究了亚得里亚海的渔获物,并注意到在第一次世界大战期间(1914-1918年),捕捞的肉食性鱼类的百分比有所增加。因为这种现象恰好发生在捕鱼量已大大减少的战争年代,这使他感到困惑不已。后来,Volterra独立于洛特卡发展了自己的模型,并用它来解释D'Ancona的观察结果。[12]
之后该模型得到进一步扩展,加入了包括依赖于种群密度的猎物增长机制和由C. S. Holling发展出的功能响应机制,被称为Rosenzweig–MacArthur模型[13] 。Lotka–Volterra和Rosenzweig–MacArthur模型一直被用于解释捕猎双方自然种群的动态变化,例如哈德逊湾[14]的山猫和雪兔的种群数据,以及罗亚尔岛国家公园的麋鹿和狼的种群数据。[15]
在1980年代末,出现了Lotka–Volterra捕猎模型(泛指常规猎物依赖模型)的替代模型,即比率依赖模型或Arditi–Ginzburg模型[16]。但时至今日,猎物依赖和比率依赖模型的有效性一直存在争议。[17]
Lotka-Volterra方程在理论经济学中有很长的应用历史,最早由Richard Goodwin应用于1965[18]与1967年。[19][20]
方程的物理意义
Lotka–Volterra模型对捕猎双方的环境和种群数量演化做出了许多假设,这些假设显得过于理想化,在自然界中显得并不实际:[21]
- 猎物随时都有充足的食物。
- 捕食者种群的食物供应充足与否完全取决于猎物种群的大小。
- 各种群数量变化率与其规模成正比。
- 在此过程中,环境不会因一种物种而改变,并且忽略遗传适应性。
- 捕食者有无限的食欲。
在这种情况下,微分方程的解是确定并连续的。反过来,这也意味着捕食者和猎物的世代是持续重叠的。[22]
猎物
当猎物数量成倍增趋势时,猎物方程可表示为:
- [math]\displaystyle{ \frac{dx}{dt} = \alpha x - \beta x y. }[/math]
假定猎物具有无限的食物供应,且除非受到捕食,否则可以成倍繁殖,那么其指数增长可表示为上式中的αx。假设捕食者的捕食率,与捕食者和猎物的相遇率成正比,那么即可表示为上式中的βxy。注意如果x或y为零,则表示没有发生捕猎。
基于这两个假设,上述方程式可以理解为:猎物种群的变化率等于其自身数量的增长率减去被捕食数量的增长率。
捕食者
捕食者方程可表示为:
- [math]\displaystyle{ \frac{dy}{dt} = \delta xy - \gamma y. }[/math]
在此等式中,δxy代表捕食者种群的增长。(请注意此处与捕食率表达式虽然相似;但是使用了一个不同的常数,因为捕食者的增长速率不一定等于其捕杀猎物的速率)。另外γy表示由于自然死亡或迁徙造成的捕食者数量减少率,它在没有猎物的情况下是呈指数型衰减的。
因此,上述方程式可以理解为,捕食者种群的变化率取决于其捕杀猎物的速率减去其内在死亡(包括迁徙)率。
方程求解
对于通常的三角方程,虽然很容易处理并得到其周期解,但是其解的表达式并不简洁。[23][24]
如果该方程组中所有非负参数α, β, γ, δ均存在,那么我们可以将其中三个变量进行归一化,仅留下一个参数:由于第一个方程对于x而言是齐次的,且第二个方程对于y而言也是齐次的,因此我们可以分别对y和x的参数归一化处理为β/α 和 δ/γ,再令γ对t作归一化,最后只有α/γ保持任意,它成为了影响解的性质的唯一参数。
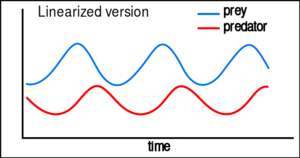
方程的线性化后求得的解类似于简谐运动曲线 [25],捕食者的数量比猎物的数量落后大概四分之一个周期。
简单示例
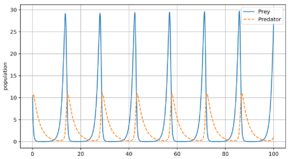
假设有两种动物,狒狒(猎物)和猎豹(捕食者)。如果初始条件是10只狒狒和10只猎豹,狒狒的增长率和死亡率分别为1.1和0.4,而猎豹的增长率和死亡率分别为0.1和0.4,且在时间轴上从初始点开始任选一段足够长的区间,那么我们可以绘制出这两个物种随时间推移的数量变化曲线。
或者也可以在相空间轨道中将其解进行参数化处理,此时就可以略去时间轴。仅用其中一个轴代表全时间段猎物的数量,而另一轴代表全时间段捕食者的数量。
对应于上面的两个微分方程,此方法可以得出约掉时间参数的一个全新的微分方程
- [math]\displaystyle{ \frac{dy}{dx} = - \frac{y}{x} \frac{\delta x - \gamma}{\beta y -\alpha} }[/math]
该方程仅包含变量x 和 y。方程的解是一条闭合曲线,可以通过分离变量法求解:对以下式子进行积分
- [math]\displaystyle{ \frac{\beta y - \alpha}{y} \,dy + \frac{\delta x - \gamma}{x} \,dx = 0 }[/math]
得到隐性关系
- [math]\displaystyle{ V = \delta x - \gamma \ln(x) + \beta y - \alpha \ln(y), }[/math]
其中V是取决于初始条件的常量,并且在每条曲线上均守恒。
另外值得注意的是,这些图说明了该方程组作为生物学模型的严重潜在问题:因为某种特定的参数选择,在每个周期中,狒狒的数量都被减少到极低的数量,但却有能力恢复(并且在极低的狒狒种群密度之下,猎豹的数量仍然很大)。这在现实中显然是不可能的,离群索居的狒狒的数量的波动,以及狒狒的家庭结构和生命周期都有可能导致狒狒种族灭绝,结果也就造成了猎豹的灭绝。按照此类方法建模出现的问题被称为"atto-fox问题","atto"这里指的是十的负十八次方。[26][27]
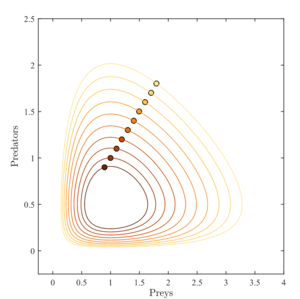
相空间图的进一步示例
一个较为合理的例子是: α = 2/3, β = 4/3, γ = 1 = δ. 假设x, y处于“千”级别还不到“万“。圆圈代表从x = y = 0.9 到 1.8时猎物和捕食者的初始条件,步长为0.1,不动点为(1,1/2)。
系统动力学
在该模型系统中,捕食者在有大量猎物的情况下肆意增长,但最终它们会因为食物供应不足而下降。随即捕食者数量变低,猎物数量将再次增加。这样形成的动力学系统以增长和下降为周期持续下去。
种群平衡
当捕猎双方种群数量都没有变化时,即当式中两个导数都等于0时,模型就会出现种群平衡:
- [math]\displaystyle{ x(\alpha - \beta y) = 0, }[/math]
- [math]\displaystyle{ -y(\gamma - \delta x) = 0. }[/math]
对上面的方程组进行求解,得到:
- [math]\displaystyle{ \{y = 0,\ \ x = 0\} }[/math]
及
- [math]\displaystyle{ \left\{y = \frac{\alpha}{\beta},\ \ x = \frac{\gamma}{\delta} \right\}. }[/math]
因此我们得到了两个平衡点(对应于上式的两个解)。
第一种解实际上代表了两种物种的灭绝。当它们的解都为0时,它们将继续无限期地保持灭绝状态。第二种解则表示两个种群都维持其当前固定数量(非零点),在简化模型中,它们无限期地保持状态不变。达到平衡时的种群数量水平取决于参数α, β, γ, 和 δ的给定值。
不动点的稳定性
不动点在原点处的稳定性可以通过求偏导数将其线性化来确定。
可以得出捕猎模型的雅可比矩阵为:
- [math]\displaystyle{ J(x, y) = \begin{bmatrix} \alpha - \beta y & -\beta x \\ \delta y & \delta x - \gamma \end{bmatrix}. }[/math]
该矩阵也可以称为群落矩阵。
第一不动点(灭绝)
当在(0, 0)的稳态下求值时,雅可比矩阵J为
- [math]\displaystyle{ J(0, 0) = \begin{bmatrix} \alpha & 0 \\ 0 & -\gamma \end{bmatrix}. }[/math]
该矩阵的特征值是:
- [math]\displaystyle{ \lambda_1 = \alpha, \quad \lambda_2 = -\gamma. }[/math]
在模型中,由于α 和 γ始终大于零,因此上述特征值的符号将始终不同。继而得到原点的不动点是鞍点。
第一不动点的稳定性非常重要。只有当它是稳定的,非零物种群体才有可能趋向于灭绝。并且在此条件下,即使种群处于初期状态,根据该动力学系统仍然可能得出两种物种都灭绝的结果。但是,由于第一不动点位于原点处是一个鞍点,因此很不稳定,进而说明模型中的两个物种都灭绝并没有那么容易。(实际上,只有在人为地彻底消灭猎物,进而导致捕食者饿死之后,才会发生这种情况。相反地,如果消灭了捕食者,那么在这个简单的模型中,猎物将不受限制地增长。)捕食者和猎物的种群数量可以无限地接近零,且仍然可以恢复。
第二不动点(震荡)
在第二个不动点求雅可比矩阵J可得:
- [math]\displaystyle{ J\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) = \begin{bmatrix} 0 & -\frac{\beta \gamma}{\delta} \\ \frac{\alpha \delta}{\beta} & 0 \end{bmatrix}. }[/math]
该矩阵的特征值是
- [math]\displaystyle{ \lambda_1 = i \sqrt{\alpha \gamma}, \quad \lambda_2 = -i \sqrt{\alpha \gamma}. }[/math]
由于特征值既是纯虚数又是共轭的,因此该不动点是椭圆的并且其解具有周期性,即在不动点周围的椭圆环上以一定频率振荡:[math]\displaystyle{ \omega = \sqrt{\lambda_1 \lambda_2} = \sqrt{\alpha \gamma} }[/math] ,其周期为:[math]\displaystyle{ T = 2{\pi}/(\sqrt{\lambda_1 \lambda_2}) }[/math]。
如上图的循环振荡所示,其等高线围绕不动点形成闭合轨道:因此捕食者和猎物的种群数量在不动点处以频率[math]\displaystyle{ \omega = \sqrt{\alpha \gamma} }[/math]循环并且无阻尼震荡。
对于不动点附近的闭合轨道,不难找到其运动常数V的值,同样包括,K = exp(V), [math]\displaystyle{ K = y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} }[/math]。
K的增加会将闭合轨道移近不动点。另外通过解决优化问题还可以获得常数K的最大值。
- [math]\displaystyle{ y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} = \frac{y^\alpha x^\gamma}{e^{\delta x+\beta y}} \longrightarrow \max\limits_{x,y\gt 0}. }[/math]
因此,在固定点(即不动点)[math]\displaystyle{ \left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) }[/math]处可以获得K的最大值,该值等于[math]\displaystyle{ K^* = \left(\frac{\alpha}{\beta e}\right)^\alpha \left(\frac{\gamma}{\delta e}\right)^\gamma, }[/math]
其中e是欧拉数
另见
- 竞争性Lotka–Volterra方程 Competitive Lotka–Volterra equations
- 广义Lotka–Volterra方程 Generalized Lotka–Volterra equation
- 互惠主义与Lotka–Volterra方程 Mutualism and the Lotka–Volterra equation
- 群落矩阵 Community matrix
- 种群动态 Population dynamics
- 渔业种群动态 Population dynamics of fisheries
- Nicholson–Bailey模型 Nicholson–Bailey model
- 反应扩散系统 Reaction–diffusion system
- 富集悖论 Paradox of enrichment
- 兰切斯特定律 Lanchester's laws,有关于军事战术的微分方程组
备注
- ↑ Freedman, H. I. (1980). Deterministic Mathematical Models in Population Ecology. Marcel Dekker.
- ↑ Brauer, F.; Castillo-Chavez, C. (2000). Mathematical Models in Population Biology and Epidemiology. Springer-Verlag.
- ↑ Hoppensteadt, F. (2006). "Predator-prey model". Scholarpedia. 1 (10): 1563. Bibcode:2006SchpJ...1.1563H. doi:10.4249/scholarpedia.1563.
- ↑ Lotka, A. J. (1910). "Contribution to the Theory of Periodic Reaction". Journal of Physical Chemistry A. 14 (3): 271–274. doi:10.1021/j150111a004.
- ↑ 5.0 5.1 Goel, N. S. (1971). On the Volterra and Other Non-Linear Models of Interacting Populations. Academic Press.
- ↑ Berryman, A. A. (1992). "The Origins and Evolution of Predator-Prey Theory" (PDF). Ecology (journal). 73 (5): 1530–1535. doi:10.2307/1940005. JSTOR 1940005. Archived from the original (PDF) on 2010-05-31.
- ↑ Verhulst, P. H. (1838). "Notice sur la loi que la population poursuit dans son accroissement". Corresp. Mathématique et Physique. 10: 113–121.
- ↑ Lotka, A. J. (1920). "Analytical Note on Certain Rhythmic Relations in Organic Systems". Proc. Natl. Acad. Sci. U.S.A. 6 (7): 410–415. Bibcode:1920PNAS....6..410L. doi:10.1073/pnas.6.7.410. PMC 1084562. PMID 16576509.
- ↑ Lotka, A. J. (1925). Elements of Physical Biology. Williams and Wilkins.
- ↑ Volterra, V. (1926). "Variazioni e fluttuazioni del numero d'individui in specie animali conviventi". Accademia dei Lincei. 2: 31–113.
- ↑ Volterra, V. (1931). "Variations and fluctuations of the number of individuals in animal species living together". In Chapman, R. N.. Animal Ecology. McGraw–Hill.
- ↑ Kingsland, S. (1995). Modeling Nature: Episodes in the History of Population Ecology. University of Chicago Press. ISBN 978-0-226-43728-6.
- ↑ Rosenzweig, M. L.; MacArthur, R.H. (1963). "Graphical representation and stability conditions of predator-prey interactions". American Naturalist. 97 (895): 209–223. doi:10.1086/282272.
- ↑ Gilpin, M. E. (1973). "Do hares eat lynx?". American Naturalist. 107 (957): 727–730. doi:10.1086/282870.
- ↑ Jost, C.; Devulder, G.; Vucetich, J.A.; Peterson, R.; Arditi, R. (2005). "The wolves of Isle Royale display scale-invariant satiation and density dependent predation on moose". J. Anim. Ecol. 74 (5): 809–816. doi:10.1111/j.1365-2656.2005.00977.x.
- ↑ Arditi, R.; Ginzburg, L. R. (1989). "Coupling in predator-prey dynamics: ratio dependence" (PDF). Journal of Theoretical Biology. 139 (3): 311–326. doi:10.1016/s0022-5193(89)80211-5.
- ↑ Abrams, P. A.; Ginzburg, L. R. (2000). "The nature of predation: prey dependent, ratio dependent or neither?". Trends in Ecology & Evolution. 15 (8): 337–341. doi:10.1016/s0169-5347(00)01908-x. PMID 10884706.
- ↑ Gandolfo, G. (2008). "Giuseppe Palomba and the Lotka–Volterra equations". Rendiconti Lincei. 19 (4): 347–357. doi:10.1007/s12210-008-0023-7.
- ↑ Goodwin, R. M. (1967). "A Growth Cycle". In Feinstein, C. H.. Socialism, Capitalism and Economic Growth. Cambridge University Press. https://archive.org/details/socialismcapital0000fein.
- ↑ Desai, M.; Ormerod, P. (1998). "Richard Goodwin: A Short Appreciation" (PDF). The Economic Journal. 108 (450): 1431–1435. CiteSeerX 10.1.1.423.1705. doi:10.1111/1468-0297.00350. Archived from the original (PDF) on 2011-09-27. Retrieved 2010-03-22.
- ↑ "PREDATOR-PREY DYNAMICS". www.tiem.utk.edu. Retrieved 2018-01-09.
- ↑ Cooke, D.; Hiorns, R. W. (1981). The Mathematical Theory of the Dynamics of Biological Populations. II. Academic Press.
- ↑ Steiner, Antonio; Gander, Martin Jakob (1999). "Parametrische Lösungen der Räuber-Beute-Gleichungen im Vergleich". Il Volterriano. 7: 32–44.
- ↑ Evans, C. M.; Findley, G. L. (1999). "A new transformation for the Lotka-Volterra problem". Journal of Mathematical Chemistry. 25: 105–110. doi:10.1023/A:1019172114300.
- ↑ Tong, H. (1983). Threshold Models in Non-linear Time Series Analysis. Springer–Verlag.
- ↑ Lobry, Claude; Sari, Tewfik (2015). "Migrations in the Rosenzweig-MacArthur model and the "atto-fox" problem" (PDF). Arima. 20: 95–125.
- ↑ Mollison, D. (1991). "Dependence of epidemic and population velocities on basic parameters" (PDF). Math. Biosci. 107 (2): 255–287. doi:10.1016/0025-5564(91)90009-8. PMID 1806118.
参考文献
- Leigh, E. R. (1968). "The ecological role of Volterra's equations". Some Mathematical Problems in Biology. – a modern discussion using Hudson's Bay Company data on lynx and hares in Canada from 1847 to 1903.
- Kaplan, Daniel; Glass, Leon (1995). Understanding Nonlinear Dynamics. New York: Springer. ISBN 978-0-387-94440-1. https://archive.org/details/understandingnon0000kapl.
- Murray, J. D. (2003). Mathematical Biology I: An Introduction. New York: Springer. ISBN 978-0-387-95223-9.
- Yorke, James A.; Anderson, William N. Jr. (1973). "Predator-Prey Patterns (Volterra-Lotka equations)" (PDF). PNAS. 70 (7): 2069–2071. doi:10.1073/pnas.70.7.2069. JSTOR 62597. PMC 433667. PMID 16592100.
- Llibre, J.; Valls, C. (2007). "Global analytic first integrals for the real planar Lotka-Volterra system". J. Math. Phys. 48 (3): 033507. Bibcode:2007JMP....48c3507L. doi:10.1063/1.2713076.
相关链接
- 来自Wolfram 演示项目— 需要CDF player (free):
- Lotka-Volterra算法仿真(网络仿真)
编者推荐
书籍推荐
Chaos: Making a New Science
本书由普利茨奖获得者James Gleick撰写。它是一本易读科普书籍,侧重介绍对混沌概念的发展做出重大贡献的科学家和数学家们。
现代动力系统理论导论 Introduction to the Modern Theory of Dynamical Systems
本书提供了动力学系统理论的第一个独立的综合性论述,它是与大多数主要数学领域紧密联系在一起的核心数学学科。作者介绍并严格发展了该理论,同时为对应用程序感兴趣的研究人员提供了基本的工具和范例。该书首先讨论了几个基本但基本的示例。 这些用于制定一个渐进性质的一般研究程序,并介绍主要的理论概念和方法。该书针对从高级本科生到各级数学的学生和研究人员。应用动力学,非线性科学和混沌领域的科学家和工程师将在这个具体而清晰的演示中找到许多新见解。
集智课程推荐
圣塔菲课程:Introduction to Dynamical Systems and Chaos
本课程中,主要介绍动力学系统和混沌系统,您将学到蝴蝶效应 Butterfly effect、奇异吸引子 Attractors等基本概念,以及如何应用于您感兴趣的领域。
动力系统分析
本课程主要讲授连续和离散动力系统的定态、极限环及其稳定性分析、动力学系统的结构稳定性和常见的分支类型以及分析方法,混沌概念等。
本中文词条由Jie翻译,CecileLi、潮升阶审校,薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。