Mean-field approximation and the Curie-Weiss model

Naïve Mean-Field Approximation

For a general coupling distribution, the macroscopic observables associated with the Boltzmann distribution are usually hard to solve, thus we usually need approximations. The simplest mean-field approximation is called Naïve Mean-Field or Variational Mean-Field. It also has a strong relation to the variational inference approaches, which will be shown later.

First of all we see that once a configuration [math]\displaystyle{ \textstyle\underline\sigma^t }[/math] is given, a spin i experiences a local field as

[math]\displaystyle{ h_i=\sum_jJ_{ij}\sigma^t_j. }[/math]

As in the Glauber dynamics, the expectation of value that spin i in the "next time" when we flip spin i is given by

[math]\displaystyle{ m_i^{t+1}=\tanh(\beta\sum_iJ_{ij}\sigma_j^t). }[/math]

Then a simple approximation says that let us forget the time indices, and replace the spin values by its mean, this results to the Naïve Mean-Field approximation:

[math]\displaystyle{ m_i=\tanh(\beta\sum_iJ_{ij}m_j). }[/math]

Curie-Weiss model and the phase transition

The Curie-Weiss model is the most simple model for ferromagnets, where [math]\displaystyle{ \textstyle J_{ij}=J/n }[/math], a constant, and system is fully connected.

Without the external field (which is considered in the whole lecture) In the model there is a symmetry that for any configuration, flipping each spin to its opposite value does not alter the energy of the configuration, i.e.

[math]\displaystyle{ E(\underline\sigma)=E(-\underline\sigma). }[/math]

It means that the magnetization of each spin should be always zero, as marginal distribution for spin i has to satisfy [math]\displaystyle{ \textstyle p_i(\sigma_i)=-p_i(\sigma_i). }[/math] This is indeed the case at high temperature where [math]\displaystyle{ \textstyle \beta }[/math] is small. This is called the Paramagnetic state. However at a low temperature we can not see this state, because of the spontaneous symmetry breaking, at which point the paramagnetic state becomes unstable. We can show the phenomenon using the Naïve Mean-Field Approximation.

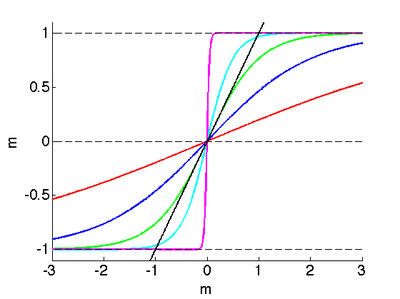
Here the couplings are identical, the mean-field equation for the magnetization simply becomes

[math]\displaystyle{ m=\tanh(\beta Jm). }[/math]

The fixed-points of above equation can be shown in the following figure where [math]\displaystyle{ \beta J=0.2, 0.5, 1, 2, 20. }[/math]