本征微观态

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索

对于开放、广泛、处于非平衡态的复杂系统，研究者们往往难以得到它们的哈密顿量、统计分布、序参量。虽然可获取的试验与观测数据越来越多，但如何更好地从这些数据出发，研究复杂系统的集体行为或相变与临界现象，却依然是一道难题。

针对该问题，北京师范大学陈晓松教授与其合作者们提出了一个解决方案[1][2]，即本征微观态方法。他们从吉布斯所提出的统计系综理论出发，基于复杂系统个体的观测或模拟数据，构建复杂系统的微观态和统计系综。以描述系统微观态的高维向量作为列，系统个体的演化序列作为行，来得到归一的统计系综矩阵。他们利用奇异值分解方法，分解统计系综矩阵，很好地研究了复杂系统中本征微观态的凝聚与系统的相变。

更进一步地，陈晓松教授与其合作者们提出了本征微观态重整化群理论[3]，研究卡丹诺夫重整化群变换下本征微观态的非平庸不动点，从而对统一地处理广泛的平衡和非平衡复杂系统临界现象提供了有力的见解。

陈晓松教授团队成功地将本征微观态方法应用于二维伊辛模型、地球表面温度、中国股票价格等三类不同领域的复杂系统[1]，胡進錕等亦将此方法应用至美国民航延误的研究[4]中，这揭示了这些系统的集体行为和它们的相变与临界现象，证实了该理论框架可用于一般平衡和非平衡系统。

理论背景

系综（统计系综）

如果我们用概率来描述热系统，采用的方法一般是，设想一次又一次地重复某一个实验，来测量某一个系统的某一种性质，因为我们无法控制它们的微观性质（由系统的微观态所描述），在尝试表述这个方法时，乔赛亚·威拉德·吉布斯（Josiah Willard Gibbs）在1902年提出了系综的概念 [5]。这是一种理想化的方法，在该方法中他考虑对系统进行大量想象的“影印”，其中每一个都代表了该系统所处的一个可能状态。

在物理学，特别是在统计物理学中，在统计物理中，系综代表一定条件下，一个体系的大量可能状态的集合。换句话说，系综是系统状态的一个概率分布。对一相同性质的体系，其微观状态（比如每个粒子的位置和速度）仍然可以大不相同。更进一步地说，统计系综是统计力学中用来描述单一系统的一组粒子系统 [6]。

下面举一个例子来说明这样的表述。考虑抛一枚硬币的实验，这样一个简单的实验只有两种可能的结果，“正面”或“反面”[注 1]。原则上，如果我们能够确切地知道硬币是如何被抛出的，以及与硬币和桌子相互作用力等等信息，那么只要根据经典力学的理论进行一定的计算，实验的结果应该是完全可以预测的。实际上，关于这个实验详细的、精确的信息是无法获取的。所以对于某一次实验结果，我们不可能作出唯一的预测，可是实验的统计表述却是比较简单的。

为了展示抛掷一枚硬币的概率，我们考虑由N枚相同的硬币组成的系综（N是一个非常大的的值），当每一枚硬币都被抛掷后，系综的“面貌”在就在这张图中被展示出来了。

我们只要考虑由很大数目，[math]\displaystyle{ N }[/math]枚相似的硬币组成的一个系综，当这些硬币以同样的方式抛出，我们可以数出结果中硬币正反面的个数，进而得到正面的概率[math]\displaystyle{ p }[/math]和反面的概率[math]\displaystyle{ q }[/math]。统计理论希望能够预测这些概率。

现在考虑稍微复杂一点的掷N枚硬币的实验，由于抛掷任何一枚硬币都有两个可能的结果，那么掷N枚硬币就可以出现[math]\displaystyle{ 2×2×2×…×2=2^N }[/math]个可能结果中的任何一个。如果不是只讨论一组[math]\displaystyle{ N }[/math]枚硬币，而是考虑[math]\displaystyle{ N }[/math]个这样的组（每组有[math]\displaystyle{ N }[/math]枚硬币）所组成的系综，每组都以相似的方式抛掷硬币，那么值得我们探究的问题便是，[math]\displaystyle{ 2^N }[/math]个可能结果中，任何一个特殊的结果在系综中出现的概率为多大。

“平衡系综”的概念对统计系综的许多应用至关重要。如果每一时刻体系的统计系综中，呈现任一特殊事件的体系数目是一样的（或等价地表示为：如果这个系综中任一特殊事件出现的概率与时间无关），那么就说这个系综是与时间无关的。换句话说，尽管一个机械系统肯定会随着时间的推移而演变，但系综并不一定会发生演变。事实上，如果系综包含了系统的所有过去和未来阶段，那么它就不会演变。这样的统计描述就为平衡提供一个非常清楚的定义：如果孤立宏观体系的一个统计系综是与时间无关的，那么这样一个体系就称为处于平衡[5]。

吉布斯定义了三种主要的系综[5]：

（1）微正则系综（microcanonical ensemble）：系综里的每个体系具有相同的能量[5]。

（2）正则系综（canonical ensemble）：系综里的各体系可以和外界环境交换能量，这种能量交换将确定（并且定义）了系统的温度[5]。

（3）巨正则系综（grand canonical ensemble）：是正则系综的推广，各体系可以和外界环境交换能量和粒子，但系综内各个体系有相同的温度和化学势[5]。

在系综中，物理量的变化范围与其本身大小的比值会随着体系的增大而减小。那么对于一个宏观体系来说，从各种系综计算出的物理量的差异将趋于零。

相变

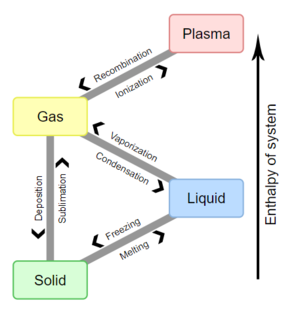
在化学、热力学和其他许多相关领域，相变（或相位变化）是指介质的一种状态（由某些参数确定）和另一种状态（参数值不同）之间的过渡物理过程。这个术语通常用于指固体、液体和气体，等离子体（少数情况下）等物质的基本状态之间的变化。

此图显示了不同相变的命名法

举例来说，热力学系统的一个阶段和物质状态具有统一的物理特性。在某一介质的相变过程中，由于外部条件的变化，如温度、压强或其他条件的变化，介质的某些属性发生的变化，往往是不连续的。比如液体在加热到沸点时，可能变成气体，导致体积的突然变化。这种对发生转变的外部条件的测度，称为相变。相变通常发生在自然界中，并且今天在许多技术中也常常被使用。

保罗·埃伦费斯特（Paul Ehrenfest）提出了如下关于相变的一种分类 [7] ：相变的级（order）是在[math]\displaystyle{ T_C }[/math]处吉布斯自由能[math]\displaystyle{ G }[/math]（或者[math]\displaystyle{ \mu }[/math]）的微分显示不连续性的最低的阶数。那么一级相变（rstorder phase transition）包含潜热，因为熵[math]\displaystyle{ S }[/math]（[math]\displaystyle{ G }[/math]的一阶微分）此时显示出不连续性，体积[math]\displaystyle{ V }[/math]（也是[math]\displaystyle{ G }[/math]的一阶微分）也显示出一个并不连续的跳跃 [8]。热容[math]\displaystyle{ C }[/math]是[math]\displaystyle{ G }[/math]的二阶微分，并且也显示出一个尖锐的跳跃，压缩系数[math]\displaystyle{ \beta }[/math]也是如此。一级相变的例子包括固液相变、固气相变以及气液相变。

根据埃伦费斯特的分类，二级相变（second-order phase transition）没有潜热，因为熵[math]\displaystyle{ S }[/math]没有显示出不连续性，并且体积[math]\displaystyle{ V }[/math]也没有不连续性，但是如热容[math]\displaystyle{ C }[/math]和压缩系数[math]\displaystyle{ \beta }[/math]等量却依然不连续 [8]。二级相变的例子包括超导相变，或者[math]\displaystyle{ \beta }[/math]黄铜中的有序无序转变。

然而，在研究相变时我们所使用的这种方法，存在一个很大的问题。我们在热力学中常所作这样一个近似，粒子的数目很大，以至于平均性质（如压强和密度）能够被很好地定义，但这种近似在相变时将会失效。在接近相变时，涨落增加，所以在非常接近相变温度时，系统的行为并不遵循我们所预期的分析。在所有的长度标度下，这个临界区域会由涨落所表征。

不符合埃伦费斯特分类的相变的第一个例子是1944年由拉尔斯·昂萨格（Lars Onsager）发现的Ising模型的精确解。在接下来的几十年里，埃伦费斯特分类法被一个简化的分类方案所取代，这个方案不在此过多赘述，感兴趣的读者可以参见相变。

临界点与临界现象

在热力学中，一个临界点（或临界状态）就是相平衡曲线的终点。最突出的例子是液-汽临界点，它是压力-温度曲线的终点，它指明了液体和其蒸汽可以共存的条件。在较高的温度下，气体不能仅靠压力来液化。在由临界温度[math]\displaystyle{ T_C }[/math]和临界压力[math]\displaystyle{ p_C }[/math]定义的临界点，相边界消失。其他例子包括混合物中的液-液临界点，以及在没有外部磁场的情况下的铁磁体-准磁体转变 [9]。

该图为典型的相图。其中虚线部分表示了水的反常行为

为使表述简单明晰，临界点的一般概念我们通过液-汽临界点来介绍。

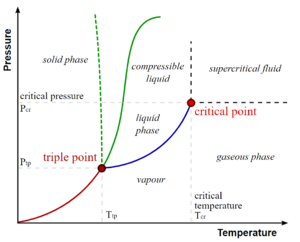
右图显示了纯物质的P-T图。众所周知，固相、液相和汽相通过相边界分离，即两相可以共存的压力-温度组合。在三相点，所有三个相可以共存。然而，在临界温度[math]\displaystyle{ T_C }[/math]和临界压力[math]\displaystyle{ p_C }[/math]时，液-汽边界终止于一个点，也就是临界点。

在临界点附近，液体和蒸汽的物理性质发生了巨大变化，两相变得越来越相似。在临界点，只有一个相存在。这意味着在临界点[10][11][12]：

[math]\displaystyle{ \left(\frac{\partial p}{\partial V}\right)_T = 0, }[/math]
[math]\displaystyle{ \left(\frac{\partial^2p}{\partial V^2}\right)_T = 0. }[/math]

由右图可见，液相和气相区域之间的边界线在临界点终结，因此有可能通过选取一条穿过相图、避免不连续变化的路径“逃脱”清晰的相变。对于高于临界温度（如水为647K）的温度，气态和液态仅可以通过它们的密度来区分。气态和液态之间的转变不涉及对称性的变化，所以可通过围绕临界端点改变状态，从而避免明显的相变。与此相比较，固液相变涉及对称性的变化，因此熔化曲线没有临界点。关于更多涉及对称性的变化的定义与示例，参见对称性破缺。

平衡态与非平衡态

“平衡”这个词意味着一种平衡的状态。平衡热力学，通常被认为起源于对卡诺循环的分析。在这个典型的系统里，比如一缸气体，最初处于其自身的内部热力学平衡状态，通过燃烧反应的热输入而失去平衡。然后通过一系列的步骤，随着系统进入最终的平衡状态，功被释放出来。

在平衡态下，系统内的热力学势或驱动力处于完全平衡状态。平衡热力学的一个核心目标是：给定一个处于明确的热力学平衡初始状态的系统，受到被精确规定的约束，计算当约束被外部施加的干预改变时，一旦系统达到新的平衡，系统的状态将会是什么。平衡态在数学上是通过寻求热力学势函数的极值来确定的，其性质取决于施加在系统上的约束。例如，在恒定温度和压力下的化学反应，将在吉布斯自由能[math]\displaystyle{ G }[/math]最小和熵[math]\displaystyle{ S }[/math]最大时达到平衡 [13]。

平衡热力学与非平衡热力学不同，对于后者而言，被分析系统的状态通常不是均匀的，而是在能量[math]\displaystyle{ E }[/math]、熵[math]\displaystyle{ S }[/math]和温度[math]\displaystyle{ T }[/math]分布上会发生局部变化。相比之下，在平衡热力学中，系统的状态将被认为是均匀的，由温度、压力或体积等量宏观定义的。系统是根据从一个平衡状态到另一个平衡状态的变化来研究的，这样的变化被称为热力学过程。

几乎所有在自然界中发现的系统都不是在热力学平衡中，因为它们正在随着时间变化或者可以被触发而发生变化，并且不断地和其他系统交换物质和能量以及参与化学反应。然而，某些系统和过程在某些程度上足够接近于热力学平衡态，允许目前已有的非平衡态热力学对其进行可行的精确描述。然而，在许多自然系统和过程中，由于非变分动力学的存在，使得自由能的概念并不存在，因此总是远远超出非平衡热力学方法的范围 [14]。

对于平衡态的研究，使用了“准静态过程”的理想化概念。准静态过程是一种概念上沿着热力学平衡状态连续路径的平滑数学过程。它只可能是微分几何的练习，而不是现实中可能发生的过程 [15]。此外，非平衡态热力学试图描述连续的时间进程，这需要它的状态变量与平衡态热力学的状态变量之间有非常密切的联系。这极大地限制了非平衡态热力学的范围，并对其概念框架提出了严格的要求 [16]。

不同于前文所述的平衡态，非平衡态要复杂得多，它可能存在更多广延量的涨落。边界条件施加给它们某些强度量，如温度梯度或形变集体运动（剪切运动、涡旋等），通常称为热力学力。在这里，我们必须强调，这里并没有像平衡态热力学中，熵的热力学第二定律那样定义能量的静态非平衡性质的一般定律。这就是为什么在这种情况下，应该考虑一个更一般的Legendre变换（也就是拓展的马休势，extended Massieu function）。

微观态与宏观态

我们不妨用一个简单的例子来介绍微观态与宏观态。

设想一个大盒子里，放有100个完全相同的硬币。盖上盒盖后，用力并持续足够长的时间摇晃盒子，随后打开盒盖朝里看，有些硬币正面朝上，有些硬币反面朝上 [注 2]，有大量可以获得的可能组态（准确地说，应该是[math]\displaystyle{ 2^{100} }[/math]种，大约为[math]\displaystyle{ 10^{30} }[/math])。这里我们假定，这些不同组态中的每一种，均是等可能出现的。因此每种可能组态出现的概率约为[math]\displaystyle{ 10^{-30} }[/math]。我们称上述每一种特定的组态（configuration），为该系统的一个微观态（microstate）。这些微观态的某一个例子是：“一号硬币正面朝上，二号硬币正面朝上，三号硬币反面朝上，……，一百号硬币反面朝上”。为了辨别一个微观态，我们可能需要单独地辨别每一个硬币，这的确令人烦躁，但是这毕竟只是在简单地数数：有多少硬币正面朝上，有多少硬币反面朝上（例如，有53枚正面朝上，47枚反面朝上)。这样的分类称为该系统的一个宏观态（macrostate）。但值得注意的是，每个宏观态并不是等可能出现的。例如，在约为[math]\displaystyle{ 10^{30} }[/math]个可能的组态（微观态）中，50枚硬币正面朝上，50枚硬币反面朝上的组态数为[math]\displaystyle{ \frac{100!}{50!×50!}≈4×10^{27} }[/math]；53枚硬币正面朝上，47枚硬币反面朝上的组态数为[math]\displaystyle{ \frac{100!}{53!×47!}≈3×10^{27} }[/math]；100枚硬币正面朝上，0枚硬币反面朝上的组态数为1。

这样看来，100枚硬币正面全朝上的结果是不太可能发生的，因为这个宏观态只含有一个微观态。当然，有53枚正面和47枚反面的一个特定微观态也同样也不太可能发生，这是因为还有将近[math]\displaystyle{ 3×10^{27} }[/math]个有53枚正面和47枚反面的、看上去与之极端相似的其他微观态存在。

这个简单的例子说明了两个关键点：

（1）可以用数量巨大的、同等可能的微观态描述一个系统；

（2）实际测量的是系统宏观态的一个性质，但各个宏观态并不是同等可能出现的，因为不同宏观态对应不同数量的微观态。

系统最可能所处的宏观态，是对应于最多微观态数的宏观态。

热力学系统的行为，与上面考虑的例子中的情况非常类似。要指定一个热力学系统的一个微观态，就需要给出系统中每一个原子的微观位形 [注 3]（configuration，可能是位置和速度或者能量）。但值得注意的是，我们通常不可能测量出系统处在哪一个微观态。另一方面，仅仅给出一个热力学系统的宏观性质（如压强，总能量或者体积），我们就能指定该系统的个宏观态。举例来说，在体积[math]\displaystyle{ 1m^3 }[/math]中压强为105Pa的气体的一个宏观位形，通常会与大量的微观态相联系。

本征微观态及其演化

对于一个由[math]\displaystyle{ N }[/math]个主体组成的复杂系统，我们可以从实验测量或计算机模拟中获得主体的状态[1]。依次使用时间[math]\displaystyle{ t=1, 2, … ,M }[/math]的状态，我们可以得到主体[math]\displaystyle{ i=1,2, … , N }[/math]的状态序列[math]\displaystyle{ S_i(t) }[/math]。

一个主体[math]\displaystyle{ i }[/math]的平均状态是 [math]\displaystyle{ \begin{eqnarray}\langle {S}_{i}\rangle =\displaystyle \frac{1}{M}\displaystyle \sum _{t=1}^{M}{S}_{i}(t)\end{eqnarray} }[/math]。在某个时间[math]\displaystyle{ t }[/math]，主体[math]\displaystyle{ i }[/math]有一个波动 [math]\displaystyle{ \begin{eqnarray}\delta {S}_{i}(t)={S}_{i}(t)-\langle {S}_{i}\rangle\end{eqnarray} }[/math]。这里定义一个具有所有主体的波动的微观态，它由一个[math]\displaystyle{ N }[/math]维矢量表示： [math]\displaystyle{ \begin{eqnarray}\delta {\boldsymbol{S}}(t)=\left[\begin{array}{c}\delta {S}_{1}(t)\\ \delta {S}_{2}(t)\\ \vdots \\ \delta {S}_{N}(t)\end{array}\right]\end{eqnarray} }[/math]。

有了[math]\displaystyle{ M }[/math]个微观态，我们可以组成一个复杂系统的统计系综。这个系综由一个[math]\displaystyle{ N×M }[/math]的矩阵[math]\displaystyle{ \boldsymbol{A} }[/math]来描述，其元素为[math]\displaystyle{ \begin{eqnarray}{A}_{{it}}=\displaystyle \frac{\delta {S}_{i}(t)}{\sqrt{{C}_{0}}}\end{eqnarray} }[/math]，其中 [math]\displaystyle{ {C}_{0}={\sum }_{t=1}^{M}{\sum }_{i=1}^{N}\delta {S}_{i}^{2}(t) }[/math]，[math]\displaystyle{ \boldsymbol{A} }[/math]的列序与微观态的演变相一致。

[math]\displaystyle{ t }[/math]和[math]\displaystyle{ t^{\prime} }[/math]的微观态之间的相关性由它们的矢量乘积定义：[math]\displaystyle{ \begin{eqnarray}{C}_{{tt}^{\prime} }=\delta {\boldsymbol{S}}{\left(t\right)}^{{\rm{T}}}\cdot \delta {\boldsymbol{S}}(t^{\prime} )=\displaystyle \sum _{i=1}^{N}\delta {S}_{i}(t)\delta {S}_{i}(t^{\prime} )\end{eqnarray} }[/math] [2]。 以[math]\displaystyle{ {C}_{tt}^{\prime} }[/math]作为其元素，我们可以得到一个[math]\displaystyle{ M×M }[/math]的微观态相关矩阵：[math]\displaystyle{ \begin{eqnarray}{\boldsymbol{C}}={C}_{0}{{\boldsymbol{A}}}^{{\rm{T}}}\cdot {\boldsymbol{A}}\end{eqnarray} }[/math]，其轨迹[math]\displaystyle{ Tr\boldsymbol{C}={\sum }_{t=1}^{M}{C}_{tt}={C}_{0} }[/math] 。相关矩阵[math]\displaystyle{ \boldsymbol{C} }[/math]有[math]\displaystyle{ M }[/math]个特征向量[math]\displaystyle{ V_J }[/math]，其中[math]\displaystyle{ J = 1, 2, ⋯ , M }[/math]，我们可以用它们组成一个[math]\displaystyle{ M×M }[/math]的单元矩阵 [math]\displaystyle{ \boldsymbol{V}=\left[\boldsymbol{V}_1 \boldsymbol{V}_2 \ldots \boldsymbol{V}_M\right] }[/math]

此外，我们在这里考虑动态微观态[math]\displaystyle{ δS_i }[/math]和[math]\displaystyle{ δS_j }[/math]之间的相关性：[math]\displaystyle{ \begin{eqnarray}{{\boldsymbol{S}}}_{j}^{{{T}}}=\displaystyle \sum _{t=1}^{M}\delta {S}_{i}(t)\delta {S}_{j}(t)\end{eqnarray} }[/math]。以[math]\displaystyle{ K_{ij} }[/math]为元素，我们可以得到一个[math]\displaystyle{ N×N }[/math]的动态微观态的相关矩阵： [math]\displaystyle{ \begin{eqnarray}{\boldsymbol{K}}={C}_{0}{\boldsymbol{A}}\cdot {\boldsymbol{A}}^{T}\end{eqnarray} }[/math]，其轨迹[math]\displaystyle{ Tr\boldsymbol{K}={\sum }_{t=1}^{N}{K}_{ii}={C}_{0} }[/math]。相关矩阵[math]\displaystyle{ \boldsymbol{K} }[/math]有[math]\displaystyle{ N }[/math]个特征向量[math]\displaystyle{ U_I }[/math]，其中[math]\displaystyle{ I = 1, 2, ⋯ , N }[/math]，我们可以用它们组成一个[math]\displaystyle{ N×N }[/math]的单元矩阵 [math]\displaystyle{ \boldsymbol{U}=\left[\boldsymbol{U}_1 \boldsymbol{U}_2 \ldots \boldsymbol{U}_N\right] }[/math]。

根据奇异值分解[17]，统计系综可被分解为[math]\displaystyle{ A=\sum_{i=1}^r \sigma_i U_i \otimes V_i }[/math]。

这里的[math]\displaystyle{ r=min (N, M) }[/math]，其中，[math]\displaystyle{ U_i }[/math]为本征微观态，[math]\displaystyle{ V_i }[/math]为该本征微观态遵循的时间演化，⊗表示克罗内克积，其中[math]\displaystyle{ \sigma_i }[/math]表示[math]\displaystyle{ U_i }[/math]在系综中的概率，且满足归一化条件：[math]\displaystyle{ \sum_{i=1}^r \sigma_i^2=1 }[/math]。

用这样的方法，可以将原来相互关联的微观态转变为相互独立的本征微观态，就可以将最初的微观态用本征微观态进行线性组合，这个线性组合的大小与本征值[math]\displaystyle{ \sigma_i }[/math]（即权重因子）成正比，即[math]\displaystyle{ \sigma_i }[/math]越大，占比越多。

演化的傅里叶谱分析

第[math]\displaystyle{ I }[/math]个本征微观态的时间演化由[math]\displaystyle{ {{\boldsymbol{V}}}_{I}^{{\rm{T}}}=\left[{V}_{1I},{V}_{2I},\cdots ,{V}_{{MI}}\right] }[/math]来进行描述[1]。为了获得更多关于本征微观态演变的信息，这里对[math]\displaystyle{ V }[/math]进行傅里叶级数展开，有[math]\displaystyle{ V_{t I}=\sum_{n=0}^{M-1} b_{n I} \mathrm{e}^{\mathrm{i} \frac{2 \pi}{M} n t} }[/math]，其中傅里叶系数为[math]\displaystyle{ b_{n I}=\frac{1}{M} \sum_{t=0}^{M-1} V_{t I} \mathrm{e}^{-\mathrm{i} \frac{2 \pi}{M} n t} }[/math]。

为了表征不同频率的比例，这里引入了傅里叶功率谱密度（Fourier power spectrum density）[math]\displaystyle{ I_n=\frac{\left|b_n^I\right|^2}{\sum_{n=0}^{M-1}\left|b_n^I\right|^2} }[/math]，这将可以展示其周期[math]\displaystyle{ T_n=M/n }[/math]。

本征微观态和相变的凝聚

一般来说，在一个无序的复杂系统中并不存在一个主要的本征值和微观态，但当我们将微观态转变为本征微观态时，原来的每个微观态都可以看作一系列的本征微观态的线性求和[1]。

如果一个概率振幅[math]\displaystyle{ σ }[/math]成为主导，以至于它在[math]\displaystyle{ M → ∞ }[/math]和[math]\displaystyle{ N → ∞ }[/math]时能够取得一个有限的极限，那么在统计集合中就会出现本征微观态[math]\displaystyle{ {\boldsymbol{A}}_{I}^{e} }[/math]的凝聚，这类似于玻色气体里的玻色-爱因斯坦凝聚。一个本征微观态的凝聚，表现为有限比例的无限本征微观态共享这个本征微观态。一个新的相将出现在系统中，而新相的特征是本征微观态[math]\displaystyle{ U_I }[/math]，新相的演变，可以通过[math]\displaystyle{ V_I }[/math]来描述。

本征微观态重整化群理论

重整化群

在理论物理中，重整化群（renormalization group）是一个在不同长度标度下考察物理系统变化的数学工具。标度上的变化称为“标度变换”。重整化群与“标度不变性”和“共形不变性”这些概念的关系较为紧密。共形不变性包含了标度变换，它们都与自相似有关。在重整化理论中，系统在某一个标度上自相似于一个更小的标度，但描述它们组成的参量值不相同。系统的组成可以是原子，基本粒子，自旋等。系统的变量是以系统组成之间的相互作用来描述。

下面我们通过重整化群的一个简单例子——块自旋重整化群来帮助理解。这是由利奥·菲利普·卡达诺夫（Leo Philip Kadanoff）在1966年推导出来的。 [18]

块自旋示意图

首先考虑一个固体，如图所示，原子以二维正方形形式排列。假设每一个原子只与它最邻近的原子有相互作用，且这一系统的温度为[math]\displaystyle{ T }[/math]，相互作用的强度可以使用耦合常数[math]\displaystyle{ J }[/math]来描述。这一物理系统可以用[math]\displaystyle{ H(T, J) }[/math]来表达。

现在，我们把这个系统分为有着[math]\displaystyle{ 2\times 2 }[/math]个方块的块区，进而用块变量来描述这个系统，这些变量可以是块内变量的平均数。我们假设这些块变量可以用相同的方程来描述，只不过参数[math]\displaystyle{ T }[/math]和[math]\displaystyle{ J }[/math]不同（事实上这一假设当然并不成立，但在实际应用中这一近似已足够好）。

原本这个系统内可能有较多的原子，但现在，在问题重整化后，只有四分之一个原子需要求解。如果按照上面的方法再迭代一次，就可以得到[math]\displaystyle{ H(T'', J'') }[/math]，这次只需要计算最初的十六分之一个原子。当然，最好的结果是能够不断迭代，直到只剩下一个最大的块区。一般来说，当迭代很多次后，重整化群变换将趋向于一个不动点上的数。

威尔逊在卡丹诺夫的基础上进一步发现，系统经过块自旋变换后，可以通过重标变换的方式恢复到和原有模型一致，并指出这样的变换操作可以构成一个半群（粗粒化过程不可逆，所以没有逆元），并将其命名为重整化群。

在临界点处，由于关联长度趋于无穷大，无穷大的量在重整化群变换后仍然是无穷大，这同时也对应着群作用下的不动点。所以威尔逊创造性地将物理上的临界点与群作用下的非平庸不动点结合在一起，提出了一系列基于系统哈密顿量的重整化群理论，来研究系统的临界性质[19][20]。

本征微观态的重整化群变换

二维伊辛系统在重整化变换后，第一大本征微观态权重（σ1）体现出的(a)低温不动点和(b,c)高温不动点，以及其满足的标度形式

对于大量需要研究的复杂系统，其能量函数、系统状态分布函数和序参量都是未知。在这种情况下，前面所介绍的基于哈密顿量的重整化群理论就面临很大的挑战。为研究复杂系统的相变，可以使用基于实验数据或者计算模拟数据的本征微观态方法 [2]。

对于[math]\displaystyle{ N }[/math]个个体组成的系统，我们通过收集每个个体随时间演化的数据来构成系综矩阵。通过对系综矩阵的奇异值分解，可以将原复杂系统分解成不同的本征模式（特征向量的直积）以及模式所对应的权重（特征值）的线性组合。在该理论体系下复杂系统的相变与临界现象可通过本征微观态的凝聚来确定，这类似于玻色气体的玻色-爱因斯坦凝聚，即宏观数量玻色子在极低温下处于基态能级。

利用本征微观态理论不需要提前预知系统哈密顿量具体形式的优点，可以将重整化群思想引入本征微观态理论中。在研究了不同维度的伊辛模型在经过卡丹诺夫块变换之后，系统本征微观态的权重，即本征值，在变换前后的关系。发现系统本征值经过变换后存在三个不动点，分别对应系统处于高温极限、低温极限以及临界点处。其中高、低温极限下为平庸的不动点，其变换后的本征值满足： [math]\displaystyle{ \sigma_1^b=b^\omega \sigma_1 }[/math]，[3]其中高温下[math]\displaystyle{ ω=d/2 }[/math]，低温下[math]\displaystyle{ ω=0 }[/math]，[math]\displaystyle{ d }[/math]为系统的空间维度。

在临界点处为非平庸的不动点，变换后的本征值满足： [math]\displaystyle{ \sigma_1^b(t, h ; L / \widetilde{a})=\sigma_1\left(t_b, h_b ; L / b \tilde{a}\right) }[/math] 其中[math]\displaystyle{ t_b=t b^{1 / v}, h_b=h b^{1 / v} }[/math]为重整化的温度和外场强度。

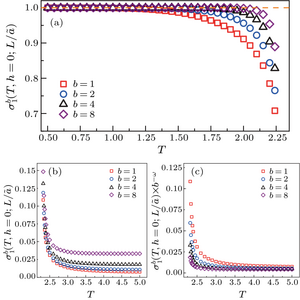
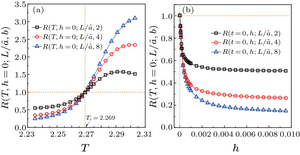
二维伊辛系统在重整化变换后，第一大本征微观态权重（σ1）在临界点处为非平庸不动点，并满足标度关系。

结合之前研究所给出[math]\displaystyle{ σ_1 }[/math]的在临界点处满足的有限尺度标度形式[math]\displaystyle{ \sigma_1\left(t, h ; \frac{L}{\tilde{a}}\right)=V^{-\bar{\beta}} F_1\left(t V^{\frac{1}{\bar{v}}}, h V^{\frac{1}{\bar{v}_h}}\right) }[/math] [2]，我们可以获得系统本征值在重整化群变换后的关系为： [math]\displaystyle{ \sigma_1^b\left(t, h ; \frac{L}{\tilde{a}}\right)=b^{\frac{\beta}{v}} \sigma_1\left(t, h ; \frac{L}{\tilde{a}}\right) }[/math]，其中[math]\displaystyle{ \sigma_1^b }[/math]为经过尺寸为[math]\displaystyle{ b \tilde{a} }[/math]的元胞变换后的本征值，[math]\displaystyle{ σ_1 }[/math]为原系统的本征值。该关系分别在一维，二维和三维伊辛模型中得到了检验，右图为二维伊辛模型的结果。

简单应用

对二维伊辛系统，通过确定重整化变换后的R函数的不动点，可以获得系统的(a)临界温度和(b)临界外场强度

上面所给出的重整化群变换关系，具有一系列非常好的性质，可以帮助我们确定系统临界点，求解临界指数，下面仍以二维伊辛模型为例进行分析。 首先我们可以定义系统第二大本征值和第一大本征值之比[math]\displaystyle{ r\left(t, h ; \frac{L}{\tilde{a}}\right)=\sigma_2 / \sigma_1 }[/math]，作为描述系统临界性质的一个标度函数。该标度函数经过重整化变换之后与变换之前的比值[math]\displaystyle{ R }[/math]，在临界点处具有不动点。即[math]\displaystyle{ R\left(t, h ; \frac{L}{\widetilde{a}}, b\right)=\frac{r(t, h ; L / \widetilde{a})}{r(r, h ; L / b \widetilde{a})} }[/math]。

在[math]\displaystyle{ t=0 }[/math]或者[math]\displaystyle{ h=h_c }[/math]时，[math]\displaystyle{ R }[/math]的值与重整化参数[math]\displaystyle{ b }[/math]无关，并且[math]\displaystyle{ R_c=1 }[/math]；根据此性质，我们可以做出不同参数[math]\displaystyle{ b }[/math]下的[math]\displaystyle{ R }[/math]曲线，根据曲线的交点所对应的温度或者外场强度来确定系统的临界点。

当系统外场（[math]\displaystyle{ h=0 }[/math]）不变，温度为[math]\displaystyle{ t_0 }[/math]时，根据系统本征值在重整化群变换下的关系可知： [math]\displaystyle{ \sigma_1^b\left(t_0, 0 ; \frac{L}{\tilde{a}}\right)=b^{\frac{\beta}{v}} \sigma_1\left(t_0, 0 ; \frac{L}{\tilde{a}}\right) }[/math]。

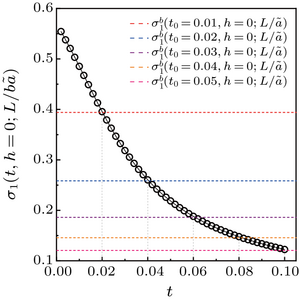
同时，如果我们考虑一个尺寸为[math]\displaystyle{ \frac{L}{b \tilde{a}} }[/math]的系统的本征值[math]\displaystyle{ \sigma_1\left(t, 0 ; \frac{L}{b \tilde{a}}\right) }[/math]。通过调节该系统的温度，使得有[math]\displaystyle{ \sigma_1^b\left(t_0, 0 ; \frac{L}{\tilde{a}}\right)=\sigma_1\left(t_0^b, 0 ; \frac{L}{b \tilde{a}}\right) }[/math]。则可求得系统的临界指数[math]\displaystyle{ v }[/math]为[math]\displaystyle{ v=\ln b / \ln \left(t_0^b / t_0\right) }[/math]，同理在只考虑外场时，将有[math]\displaystyle{ v_h=\ln b / \ln \left(h_0^b / h_0\right) }[/math]。

[math]\displaystyle{ \sigma_1(t, 0 ; L / b \tilde{a})=\sigma_1^b\left(t_0, 0 ; L / \tilde{a}\right) }[/math]在不同[math]\displaystyle{ t_0 }[/math]下二维Ising模型时的解

右图展现了在[math]\displaystyle{ b=2 }[/math]，不同的[math]\displaystyle{ t_0 }[/math]下，通过寻找[math]\displaystyle{ \sigma_1^b\left(t_0, 0 ; \frac{L}{\tilde{a}}\right) }[/math]和[math]\displaystyle{ \sigma_1\left(t_0^b, 0 ; \frac{L}{b \tilde{a}}\right) }[/math]的交点所对应的[math]\displaystyle{ t_0^b }[/math]，求得二维伊辛模型有[math]\displaystyle{ v=\frac{\ln 2}{\ln \left(\frac{0.02}{0.01}\right)}=\frac{\ln 2}{\ln \left(\frac{0.04}{0.02}\right)}=\frac{\ln 2}{\ln \left(\frac{0.06}{0.03}\right)}=\frac{\ln 2}{\ln \left(\frac{0.08}{0.04}\right)}=\frac{\ln 2}{\ln \left(\frac{0.1}{0.05}\right)}=1 }[/math]。

这里提出的本征微观态重整化群理论，规避了传统理论需知道系统的哈密尔顿量、微观态的概率分布和序参量的要求，能统一地研究平衡和非平衡复杂系统的临界行为。

应用

在平衡系统中

伊辛模型（Ising Model），是用来解释铁磁系统相变的一个简单模型。在相当长时间的探索中，人们逐渐认识到了它作为相变模型的普适性，并且发现伊辛模型可以用来对几乎所有有趣的热力学现象进行建模，甚至包括在物理之外的其他学科中。毫不夸张地说，伊辛模型是统计物理中迄今为止唯一的一个同时具备表述简单、内涵丰富、应用广泛这三种优点的模型。


我们考虑有这么一个模型：具有方形几何结构的、具有周期性边界条件的三维伊辛模型（Ising model）[1]。[math]\displaystyle{ N = L × L × L }[/math]的哈密顿方程是 [math]\displaystyle{ \begin{eqnarray}H=-J\displaystyle \sum _{\langle i，j\rangle }^{N}{S}_{i}{S}_{j}\end{eqnarray} }[/math]， 其中[math]\displaystyle{ S_i=±1 }[/math]，[math]\displaystyle{ ⟨i, j⟩ }[/math]表示对最近邻域的所有自旋进行求和。这个模型的系统大小为[math]\displaystyle{ L }[/math]，还原温度[math]\displaystyle{ T = k*BT/J }[/math]。我们可以使用Wolff算法[21]来获得系统的微观态，这个算法可以翻转一簇自旋而不是单一自旋。


在有限伊辛系统中，不存在对称性破缺。因此[math]\displaystyle{ ⟨Si⟩ = 0 }[/math]，[math]\displaystyle{ δSi(t) = Si(t) }[/math]。在时间[math]\displaystyle{ t处 }[/math]的微观态是 [math]\displaystyle{ \delta \boldsymbol{S}(t)=\left[\begin{array}{c} \delta S_1(t) \\ \delta S_2(t) \\ \vdots \\ \delta S_N(t) \end{array}\right] }[/math]。利用这些微观态，我们得到系综矩阵[math]\displaystyle{ \boldsymbol{A} }[/math]，其元素为[math]\displaystyle{ A_{i t}=\frac{\delta S_i(t)}{\sqrt{C_0}} }[/math]，其中[math]\displaystyle{ C_0 = M·N }[/math]。

在（A）[math]\displaystyle{ T^{*}=5.5116 }[/math]、（B）[math]\displaystyle{ T^{*}=4.5116 }[/math]、（C）[math]\displaystyle{ T^{*}=3.5116 }[/math]时，与[math]\displaystyle{ U1,U2,U3 }[/math]等距的四张截面图


下面我们继续通过研究本征微观态[math]\displaystyle{ U1 }[/math]的空间分布，来观察相变的特性。对于一个在三维空间的本征微观态，我们给出了四个等距的截面图来展示其空间分布。其中，在

[math]\displaystyle{ T^{*}=5.5116 }[/math]时（高于临界温度），从图中可以看到，这些本征微观态中的自旋簇都具有微小尺寸，且在空间中随机分布。在[math]\displaystyle{ T^{*}=4.5116 }[/math]时（接近临界温度）以及在[math]\displaystyle{ T^{*}=3.5116 }[/math]时（低于临界温度），最大的本征微观态EM1将产生一个凝聚。这表明，当本征微观态的概率变得有限时，就会出现一个铁磁相变。

在（A）[math]\displaystyle{ T^{*}=5.5116 }[/math]、（B）[math]\displaystyle{ T^{*}=4.5116 }[/math]、（C）[math]\displaystyle{ T^{*}=3.5116 }[/math]时，三个最大本征微观态随时间的演化图


右图显示了临界点周围的本征微观态的演变，这与Wolff算法 [21]中阐明的动力学相关。可以发现，[math]\displaystyle{ V_{tI} }[/math]随着时间[math]\displaystyle{ t }[/math]在[math]\displaystyle{ 0 }[/math]附近波动。

在地球系统中

气候问题是人类社会得以拥有稳定发展的最重要因素之一，显著的气候变迁可能直接或间接地对物种进化、种族迁徙、社会变革等产生影响[22]。能否良好地分析与解释地球气候，确乎成为关乎人类福祉的重大命题。所有复杂系统都由无数不同的、相互作用的个体组成，而这些个体又可能受大量不同、随机的因素支配。这些复杂的因素甚至可能是混沌的，如地球气候系统，初值的微小差异可能带来后续的完全不同的演化进程。但是，复杂系统往往具有很好的普适性（Universal-Examples of Behavior-sity）[23]，这使得刻画系统中所有可能状态的集合成为可能。

地球系统科学起源于20世纪前期，经过近百年的发展，行星的观测运动、地球系统模型的健全，为综合性科学的发展提供了动力。对于地球系统的稳定性问题，尤其是气候问题，是涉及整个地球系统的非线性[24]、突变与临界点的相互作用[25]的一大挑战。2021年诺贝尔物理学奖被颁发给真锅淑郎（Syukuro Manabe）和克劳斯·哈塞尔曼（Klaus Hasselmann）[26]，他们对复杂地球物理系统进行量化气候变化的物理建模，并且给出了对地球系统整体的可靠的趋势预测。

地球的六大本征微观态的空间分布
地球的六大本征微观态随时间演化的示意

在某个时间点[math]\displaystyle{ t }[/math]上，第[math]\displaystyle{ i }[/math]个格点的地球表面气温（SAT）是[math]\displaystyle{ T_i（t） }[/math]。在一个时间段[math]\displaystyle{ M }[/math]中，网格[math]\displaystyle{ i }[/math]的平均SAT可以被计算为[math]\displaystyle{ \left\langle T_i\right\rangle=\frac{1}{M} \sum_{t=1}^M\gt T_i(t) }[/math]，在第[math]\displaystyle{ i }[/math]个格点处的SAT的波动是[math]\displaystyle{ \delta T_i(t)=T_i(t)-\left\langle T_i\right\rangle, t=1,2, \cdots, M }[/math]，均方根偏差为[math]\displaystyle{ \Delta_i=\sqrt{\frac{1}{M} \sum_{t=1}^M \delta T_i(t)^2} }[/math]。那么，用下式可以很好地描述SAT的波动特征： [math]\displaystyle{ \delta S_i(t)=\delta T_i(t) / \Delta_i }[/math]。

我们现在引入地球的微观态为 [math]\displaystyle{ \delta \boldsymbol{S}(t)=\left[\begin{array}{c} \delta S_1(t) \\ \delta S_2(t) \\ \vdots \\ \delta S_N(t) \end{array}\right] }[/math][1]，借助从1950年1月1日到2018年12月31日的数据集，我们可以得到一个[math]\displaystyle{ N×M }[/math]的集合矩阵[math]\displaystyle{ A }[/math]，元素为[math]\displaystyle{ A_{i t}=\frac{\delta S_i(t)}{\sqrt{C_0}} }[/math]，其中[math]\displaystyle{ C_0 = M · N }[/math]。


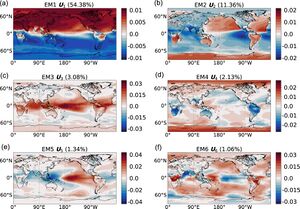
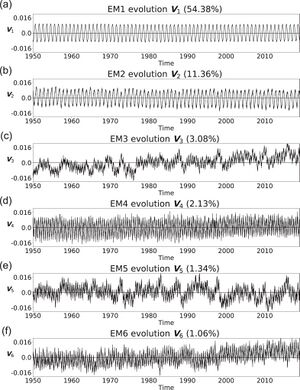
这里展示其中最大的六个本征微观态，它们可以被作为研究对象来讨论其与气候现象的关系。

本征微观态EM1展现了一个经典的日点模式，其空间格局展现出半球间的对比，在贡献了54.38%。可以发现，本征微观态EM1的演化图展示了一个十分规律的一年一次的峰值。

在本征微观态EM2中可以看到一个显著的海陆对比，这揭示了由于陆海之间热容差引起的显著的陆海之间的温度对比，其贡献了11.36%。可以发现本征微观态U2与季风分布具备联系，且SAT的变动常常被认为是季风的主要驱动力。

本征微观态EM3很好的展现了热带地区的气候波动，它占3.08%。又因为热带对流与海温有很大关系，所以本征微观态EM3也可以用于揭示热带降雨的规律。EM3 的时间序列, 存在一个明显的上升趋势, 这意味着全球变暖对热带对流和对流降水的潜在影响。有趣的是，EM3 在 1970 年代中期发现了一个临界点。这与众所周知的 1976-1977 年的气候转变是一致的[27]。

本征微观态EM4的演化图展现了一个半年度信号，在气象学中，这被称为半年度振荡（semiannual oscillation，SAO），其贡献了2.13%。其显示了本征微观态EM4与半年度振荡的相关性。

本征微观态EM5、EM6都揭示了厄尔尼诺现象的规律。研究[1]发现，本征微观态平均值U5与厄尔尼诺现象有相当高的相关性。

在经济系统中

最大的三个本征微观态U1、U2和U3
最大的三个本征微观态V1、V2和V3的演化
三大本征微观态V1、V2、V3（黑线）与三大指数：上证100指数、上证能源指数、上证材料指数（红线）随时间演化的对比图

物理学家对社会科学感兴趣可以说并不是什么新鲜事。例如，丹尼尔·伯努利（Daniel Bernoulli）最早提出基于效用的偏好；新古典主义经济理论的创始人之一，经济学教授欧文·费歇尔（Irving Fisher），最初也曾受训于著名的物理学家约西亚·威拉德·吉布斯 （Josiah Willard Gibbs）。[28]同样，扬·廷伯根（Jan Tinbergen）和保罗·埃伦费斯特（Paul Ehrenfest）一起学习了物理学，而他正因为开发和应用了经济过程分析的动态模型而获得了1969年的第一个诺贝尔经济学奖[29]。

经济物理学是在20世纪90年代中期由几个在统计力学领域工作的物理学家发起的。他们不满足于经济学家的传统解释和方法，应用物理学的工具和方法，首先在金融数据集上进行匹配，尝试去解释更普遍的经济现象。


在这里，我们研究股票市场的本征微观态来分析股票价格的波动模式，这里以中国大陆2010年1月4日至2020年5月26日的股票价格数据为研究对象[1]。

股票[math]\displaystyle{ i }[/math]在某个时间段的价格用[math]\displaystyle{ P_i（t） }[/math]表示。股票[math]\displaystyle{ i }[/math]在某一特定时期的平均价格通过下式来计算： [math]\displaystyle{ \left\lt P_i\right\gt =\frac{1}{M} \sum_{t=1}^M P_i(t) }[/math]，其中[math]\displaystyle{ M }[/math]指的是总的交易日数。在时间[math]\displaystyle{ t }[/math]时，股票[math]\displaystyle{ i }[/math]的价格波动为：[math]\displaystyle{ \delta P_i(t)=P_i(t)-\left\langle P_i\right\rangle }[/math]。

股票[math]\displaystyle{ i }[/math]的均方根波动为： [math]\displaystyle{ \Delta_i=\sqrt{\frac{1}{M} \sum_{t=1}^M \delta P_i(t)^2} }[/math]，一个股票[math]\displaystyle{ i }[/math]在某一时间段的状态的特点是波动减少[math]\displaystyle{ \delta S_i(t)=\frac{\delta P_i(t)}{\Delta_i} }[/math]，那么具有[math]\displaystyle{ N }[/math]个股票价格的股票市场的微观状态由向量[math]\displaystyle{ \delta \mathbf{S}(t)=\left[\begin{array}{c} \delta S_1(t) \\ \delta S_2(t) \\ \vdots \\ \delta S_N(t) \end{array}\right] }[/math]描述。我们可以得到一个[math]\displaystyle{ N×M }[/math]的系综矩阵[math]\displaystyle{ A }[/math]，元素为[math]\displaystyle{ A_{i t}=\frac{\delta S_i(t)}{\sqrt{C_0}} }[/math]，其中[math]\displaystyle{ C_0=\sum_{t=1}^M \sum_{i=1}^N \delta S_i^2(t) }[/math]。


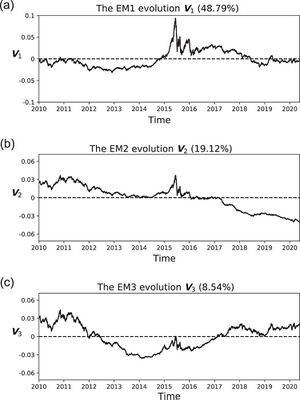
可以从右图看到，最大的三个本征微观态EM1、EM2和EM3的演变情况，它们分别展现了48.78%、19.2%和8.54%的贡献，一个本征微观态的分量表示相应股票在这个本征微观态的演变中的参与程度。我们可以看到，V1、V2、V3与上证100指数、上证能源指数、上证材料指数的演化几乎完全一致。其中，V1相关系数为[math]\displaystyle{ R=0.95 }[/math]，V2相关系数为[math]\displaystyle{ R=0.84 }[/math]，V3相关系数为[math]\displaystyle{ R=0.75 }[/math][1]。

上述本征微观态很好的描述了股票市场是本征波动模式。EM1描述了股票市场的总体趋势。EM2和EM3与股市中的能源和材料部门的演变有关。股票市场的层次性特征已经由本征微观态表现出来。

在交通系统中

随着社会经济和文化的不断快速发展，飞机已成为人们普遍选择的交通工具。民航业作为重要的基础设施服务，对国家的经济发展越来越重要。但航班延误会使空中交通效率低下，给旅客带来不好的交通体验，给航空公司带来巨大的经济损失。目前，关于航班延误的研究报告很多，但从统计物理学角度开展的研究却很少。这里我们建立了民航系统的微观态，通过这些微观态得到统计系综，从而得到其本征微观态。

首先需要定义航班的延误时间。这里超过5分钟、少于240分钟的离港延误时间作为有效延误；如果一个航班的起飞延误时间超过240分钟，我们将其视为延误航班，但延误时间不参与后续计算。在某一时间点从第[math]\displaystyle{ i }[/math]个机场出发的延误航班的数量表示为[math]\displaystyle{ n_i }[/math]，某时间点的延误率定义为：[math]\displaystyle{ P=\frac{\sum_{i=1}^N n_i}{A} }[/math]，其中[math]\displaystyle{ N }[/math]为机场的数量，[math]\displaystyle{ A }[/math]是这个时间点航班的数量。我们将机场延误强度[math]\displaystyle{ D_a }[/math]定义为当前机场所有延误航班在当前时间点的总延误时间：[math]\displaystyle{ D_a=\sum_{i=1}^{n_a} d_i }[/math]，其中[math]\displaystyle{ D_i }[/math]是被延误航班的离港延误时间。

(a)2014年8月5日、(b)2005年9月21日、(c)2008年7月15日、(d)2010年1月31日，曲线[math]\displaystyle{ P' }[/math]和[math]\displaystyle{ P }[/math]作为时间t的函数
2014年8月5日，(a)n=2，(b)n=3，(c)m=4，(d)n=5，[math]\displaystyle{ P'' }[/math]（绿色），[math]\displaystyle{ P' }[/math]（红色），[math]\displaystyle{ P }[/math]（黑色）的曲线与时间的函数关系。
修改后的（a）2014年8月5日，（b）2014年3月12日的曲线。

我们可以通过将美国机场按特定顺序排列，并将其在某一时间点的延迟强度作为元素来获得一个向量。将这个向量归一化后，我们将得到微观态[math]\displaystyle{ S^I }[/math]和[math]\displaystyle{ \left|S^I\right|^2=\left[S^I\right]^T \cdot S^I=1 }[/math]。这是飞行系统在这个时间点的微观态，它反映了延误在机场之间的分布。为了保证微观态向量具有相同的长度，我们选择12月30日运行的机场作为关键机场。民航系统的微观态由下式给出： [math]\displaystyle{ S^I=\frac{1}{\sqrt{\sum_{i=1}^N D_i^2}}\left[D_1, D_2, \cdots, D_N\right]^T }[/math]。

我们将微观态[math]\displaystyle{ I }[/math]和微观态[math]\displaystyle{ J }[/math]之间的相关关系定义为[math]\displaystyle{ C_{I J}=\left[S^I\right]^T \cdot\left[S^J\right] }[/math]。这里假设相关矩阵[math]\displaystyle{ C }[/math]具有[math]\displaystyle{ M }[/math]个有序的特征值。即有[math]\displaystyle{ \lambda_1 \geq \lambda_2 \cdots \geq \lambda_M }[/math]，以及它们相应的归一化特征向量[math]\displaystyle{ b_1, b_2, \cdots, b_M }[/math]，其中[math]\displaystyle{ b_I=\left[\begin{array}{c} b_{1 I} \\ b_{2 I} \\ \vdots \\ b_{M I} \end{array}\right] }[/math]，并有[math]\displaystyle{ C b_I=\lambda_I b_I, I=1,2, \cdots . M }[/math]。

此时，我们就可以得到本征微观态[math]\displaystyle{ E^I=\sum_{L=1}^M b_{L I} S^L, I=1,2, \cdots, M }[/math] [1]，且两个本征微观态之间的相关性被定义为[math]\displaystyle{ C_{I J}^E=\left[E^I\right]^T \cdot E^J=\sum_{l, m}^M b_{l I} C_{l m} b_{m J}=\lambda_I \delta_{I, J} }[/math]，本征微观态的权重系数被定义为[math]\displaystyle{ w_I^E=C_{I I}^E / M=\lambda_I / M }[/math]。

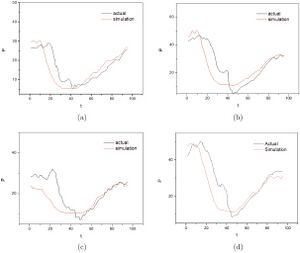
我们假设模拟的延误率为[math]\displaystyle{ P^{\prime}=a \cdot D^I \cdot S^I \cdot E^1+b }[/math]，右图显示了[math]\displaystyle{ P' }[/math]（红色）和实际延误率[math]\displaystyle{ P }[/math]（黑色）的曲线与时间的关系。可以看出，11点以后（也就是第44个时间点）[math]\displaystyle{ P' }[/math]的偏差很小，但11点以前的偏差比较大。

考虑到十点附近的最小飞行数和十点前后微观态的明显变化，我们认为较大的偏差主要是由于这段时间内这种变化的影响。我们再次假设，缺乏本征微观态是造成大偏差的原因。修改后的式子如下： [math]\displaystyle{ P^{\prime \prime}=a \cdot D^I \cdot S^I \cdot E^1+b+c \cdot D^I \cdot S^I \cdot E^2 }[/math]。

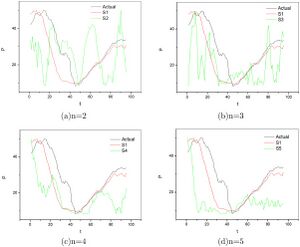
我们发现，其他本征微观态的关系曲线与十点左右的最大本征微观态相似，因此它们不能减少一天中前半段的偏差。我们可以从右图看出这一点。

为了避免第二个微观态在一天的后半段的干扰，我们只在第20个时间点和第45个时间点之间使用公式[math]\displaystyle{ P^{\prime \prime}=a \cdot D^I \cdot S^I \cdot E^1+b+c \cdot D^I \cdot S^I \cdot E^2 }[/math]，而在其他时间点使用公式[math]\displaystyle{ P^{\prime}=a \cdot D^I \cdot S^I \cdot E^1+b }[/math]。修改后的曲线如右图所示。

这意味着，某一时间点的延误率与机场间的延误分布和民航系统的延误强度有正相关关系。因此，为了降低延误率，我们可以通过调整每个机场的起飞时间，并优化延误较多的关键机场来调整机场间的延误分布[4]。

注释

  1. ↑ 我们在这里不考虑“硬币立在桌子上”这种可能性极小的事件。
  2. ↑ 我们这里依然假定不会有硬币立在盒子里面的情况出现。
  3. ↑ 按照习惯，这个前面我们称为“组态”的词，这里称为位形。

参考资料

  1. ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 Sun, Yu; Hu, Gaoke; Zhang, Yongwen; Lu, Bo; Lu, Zhenghui; Fan, Jingfang; Li, Xiaoteng; Deng, Qimin; Chen, Xiaosong (6 May 2021). "Eigen microstates and their evolutions in complex systems". Communications in Theoretical Physics. 73 (6). doi:10.1088/1572-9494/abf127.
  2. ↑ 2.0 2.1 2.2 2.3 Hu, Gaoke; Liu, Teng; Liu, Maoxin; Chen, Wei; Chen, Xiaosong (25 April 2019). "Condensation of eigen microstate in statistical ensemble and phase transition". Science China Physics, Mechanics & Astronomy. 62 (2019). doi:10.1007/s11433-018-9353-x.
  3. ↑ 3.0 3.1 Hu, Gaoke; Liu, Teng; Dong, Jiaqi; Fan, Jingfang; Liu, Maoxin; Chen, Xiaosong (7 June 2022). "Renormalization Group Theory of Eigen Microstates". Chinese Physics Letters. 39 (8). doi:10.1088/0256-307X/39/8/080503.
  4. ↑ 4.0 4.1 Qian, Wenri; Zhu, Chenping; Wang, Yanjun; Hu, Chinkun (December 2020). "Eigen microstates of particle gases for passenger flights in the United States". Chinese Journal of Physics. 68. doi:10.1016/j.cjph.2020.09.035.
  5. ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Gibbs, Josiah Willard (1902). Elementary Principles in Statistical Mechanics. New York: Charles Scribner's Sons. 
  6. ↑ Rennie, Richard; Jonathan Law (2019). Oxford Dictionary of Physcis. pp. 458 ff. ISBN 978-0198821472. 
  7. ↑ Jaeger, Gregg (1 May 1998). "The Ehrenfest Classification of Phase Transitions: Introduction and Evolution". Archive for History of Exact Sciences. 53 (1): 51–81. doi:10.1007/s004070050021. S2CID 121525126.
  8. ↑ 8.0 8.1 Blundell, Stephen J.; Katherine M. Blundell (2008). Concepts in Thermal Physics. Oxford University Press. ISBN 978-0-19-856770-7. 
  9. ↑ Stanley, H. Eugene (1987). Introduction to phase transitions and critical phenomena. New York: Oxford University Press. ISBN 0-19-505316-8. OCLC 15696711. https://www.worldcat.org/oclc/15696711. 
  10. ↑ P. Atkins and J. de Paula, Physical Chemistry, 8th ed. (W. H. Freeman 2006), p. 21.
  11. ↑ K. J. Laidler and J. H. Meiser, Physical Chemistry (Benjamin/Cummings 1982), p. 27.
  12. ↑ P. A. Rock, Chemical Thermodynamics (MacMillan 1969), p. 123.
  13. ↑ Mortimer, R. G. Physical Chemistry, 3rd ed., p. 157, Academic Press, 2008.
  14. ↑ Bodenschatz, Eberhard; Cannell, David S.; de Bruyn, John R.; Ecke, Robert; Hu, Yu-Chou; Lerman, Kristina; Ahlers, Guenter (December 1992). "Experiments on three systems with non-variational aspects". Physica D: Nonlinear Phenomena. 61 (1–4): 77–93. doi:10.1016/0167-2789(92)90150-L.
  15. ↑ Herbert Callen|Callen, H.B. (1960/1985), § 4–2.
  16. ↑ Glansdorff, P., Prigogine, I. (1971), Ch. II,§ 2.
  17. ↑ Strang, Gilbert (2009). Introduction to Linear Algebra, 4th edn. pp. 284. 
  18. ↑ Kadanoff, Leo P (1 June 1966). "Scaling laws for ising models near [math]\displaystyle{ T_c }[/math]". Physics Physique Fizika. 2 (6). doi:10.1103/PhysicsPhysiqueFizika.2.263.
  19. ↑ Wilson, Kenneth G; Kogut, John (August 1974). "The renormalization group and the ϵ expansion". Physics reports. 12 (2). doi:10.1016/0370-1573(74)90023-4.
  20. ↑ Wilson, Kenneth G (1 November 1971). "Renormalization Group and Critical Phenomena. II. Phase-Space Cell Analysis of Critical Behavior". Physical Review B. 4 (9). doi:10.1103/PhysRevB.4.3184.
  21. ↑ 21.0 21.1 Wolff, Ulli (13 October 1988). "Collective Monte Carlo updating for spin systems". Physical Review Letters. 62 (4). doi:10.1103/PhysRevLett.62.361.
  22. ↑ Carleton, Tamma A; Hsiang, Solomon M (9 September 2016). "Social and economic impacts of climate". Science. 353 (6304). doi:10.1126/science.aad9837.
  23. ↑ Fang, Fukang (2005). "Self-organization, Learning and Language". 2005 International Conference on Neural Networks and Brain. 3 (1906–1911). doi:10.1109/ICNNB.2005.1614997.
  24. ↑ Kabat, Pavel; Claussen, Martin; Dirmeyer, Paul A; Gash, John HC; de Guenni, Lelys Bravo; Meybeck, Michel; Hutjes, Ronald WA; Pielke Sr, Roger A et al. (2004). Vegetation, water, humans and the climate: A new perspective on an internactive system. Springer Science & Business Media. 
  25. ↑ Rocha, Juan C; Peterson, Garry; Bodin, Orjan; Levin, Simo (21 November 2018). "Cascading regime shifts within and across scales". Science. 362 (6421). doi:10.1126/science.aat7850.
  26. ↑ Nobel Prize, Retrieved October-14-2022
  27. ↑ Miller, Arthur J; Cayan, Daniel R; Barnett, Tim P; Graham, Nicholas E; Oberhuber, Josef M (2 October 2015). "The 1976-77 climate shift of the Pacific Ocean". Oceanography. 7 (1). doi:10.5670/oceanog.1994.11.
  28. ↑ Yale Economic Review, Retrieved October-25-2022
  29. ↑ Nobel Prize, Retrieved October-14-2022

编者推荐

本课程为北京师范大学系统科学学院陈晓松教授开设的研究生课程《复杂性与临界现象》课程回放。

相变与临界现象的研究对象逐渐由过去的无穷大平衡系统扩展到自然与社会复杂系统。我们知道，平衡系统微观态的分布是已知的，而复杂系统一般处于非平衡态，其微观态分布以及序参量一般来说都是未知的，这就给复杂系统的研究提出了挑战。针对这些问题，北京师范大学的陈晓松教授与合作者提出了一个基于本征微观态（Eigen microstates，EM）的理论方法来分析复杂系统的相变与临界现象以及其动态演化。

威尔逊1971年提出的临界现象重整化群理论，基于卡丹诺夫重整化群变换下哈密尔顿量的非平庸不动点及其附近的渐近行为，已经被广泛应用于研究哈密尔顿量已知系统的临界现象。但当前，人们亟待研究的各类复杂系统的相变与临界现象往往难以给出哈密顿量的具体形式，以至于传统方法面对很大挑战，需要另辟蹊径。最近，北京师范大学系统科学学院陈晓松教授与其合作者们基于之前本征微观态理论的研究，提出了本征微观态重整化群理论，研究卡丹诺夫重整化群变换下本征微观态的非平庸不动点，从而可统一地处理广泛的平衡和非平衡复杂系统临界现象。

取自“https://wiki.swarma.org/index.php?title=本征微观态&oldid=33646”