重整化
重整化 Renormalization是应用于量子场论 Quantum Field Theory、场的统计力学 Statistical Mechanics和自相似 Self-similar几何结构理论中的一类方法。通过重整化,可以改变计算量的值以抵消其自相互作用 Self-interaction,进而消除计算量中产生的无穷大 infinities。但是,即使在量子场论的圈图 loop diagrams中没有出现无穷大,对原拉格朗日场理论 Lagrangian (Field Theory)中出现的质量和场进行重整化也是必要的。[1]
例如,电子 Electron理论会先假定电子具有初始质量和电荷。在量子场论中,一个由诸如光子 Photon、正电子 Positron等虚粒子 Virtual Particle组成的云团围绕着初始电子并与之相互作用。考虑到周围粒子的相互作用(例如:不同能量的碰撞)表明电子-系统的行为宛如它有不同于最初假设的质量和电荷。在这个例子中,重整化在数学上用实验观察到的质量和电荷代替了最初假设的电子质量和电荷。数学和实验证明,正电子和质子 Proton等质量更大的粒子,即使存在更强烈的相互作用和更密集的虚粒子云,其电荷也与电子完全相同。
当描述大距离尺度的参数不同于描述小距离尺度的参数时,重整化指定了理论中参数之间的关系。在像欧洲核子研究中心的高能粒子加速器中,当不理想的质子-质子碰撞与同时临近的可取测量数据相互作用时,就会产生连环相撞 Pileup的概念。从物理上来说,涉及某一问题的无限量级在累积后可能会导致进一步的无限量。当把时空描述为一个时空连续统 Space-time Continuum时,某些统计的和量子力学的结构没有得到明确定义 Well-defined。为了定义它们,或者使它们毫不含糊,连续统的限制必须能够小心地移除不同尺度的晶格的“结构脚手架”。重整化过程的基础要求某些物理量(如电子的质量和电荷)等于观察到的(实验)值。也就是说,物理量的实验值虽能产生实际应用,但由于它们的经验性本质,所观察到的测量代表了量子场论中那些需要从理论基础进行更深入的推导的领域。
重整化最早发展于量子电动力学 Quantum Electrodynamics,以解释微扰理论 Perturbation Theory中的无穷积分。重整化最初被人认为是一个存疑的临时程序,甚至包括它的一些发明者。即便如此,重整化最终作为一个重要的且自洽 Self-consistent的实际尺度物理机制被物理学 Physics 和数学 Mathematics的几个领域所接受。
今天,观点发生了转变: 基于尼古拉·博戈柳博夫和 Kenneth Wilson 对重整化群 Renormalization Group的突破性见解,关注点成为连续尺度间物理量的变化,而相隔较远的尺度通过“有效的“描述彼此相关。广泛来说,所有尺度都以系统的方式联系在一起。同时,与每个尺度相关的实际物理学被适合于每个尺度的特定计算技术提取出来。威尔逊阐明了系统中哪些变量是至关重要的,而哪些又是冗余的。
重整化不同于正则化 Regularization,后者是另一种通过假设新尺度中存在新的未知的物理学以控制无穷大的技术。
经典物理中的自相互作用
无穷大问题最早出现在19世纪和20世纪初的点粒子经典电动力学中。
带电粒子的质量应包括其静电场(电磁质量)中的质能。假设这个粒子是一个带电的半径为re的球壳。场中的质能是:
- [math]\displaystyle{ m_\text{em} = \int \frac{1}{2} E^2 \, dV = \int_{r_e}^\infty \frac{1}{2} \left( \frac{q}{4\pi r^2} \right)^2 4\pi r^2 \, dr = \frac{q^2}{8\pi r_e}, }[/math]
当时re → 0,它会变得无穷大。这意味着点粒子具有无穷大的惯性 Inertia,使它无法被加速。顺带一提,使得[math]\displaystyle{ m_\text{em} }[/math]等于电子质量的这个值re被称为电子经典半径 Classical Electron Radius,它(设置[math]\displaystyle{ q = e }[/math]以及c和[math]\displaystyle{ \varepsilon_0 }[/math]的还原因子)被证明是:
- [math]\displaystyle{ r_e = \frac{e^2}{4\pi\varepsilon_0 m_e c^2} = \alpha \frac{\hbar}{m_e c} \approx 2.8 \times 10^{-15}~\text{m}, }[/math]
其中 [math]\displaystyle{ \alpha \approx 1/137 }[/math] 是精细结构常数 Fine-structure Constant精细结构常数,[math]\displaystyle{ \hbar/(m_e c) }[/math] 是电子的康普顿波长。
重整化: 球形带电粒子的总有效质量包括球壳的实际裸质量(在上述与其电场相关的质量之上)。如果允许壳体的裸质量允许为负值,则可能取一个一致的点极限。这就是所谓的重整化,洛伦兹和亚伯拉罕试图用这种方式发展出电子的经典理论。这项早期的工作启发了后来在量子场论中正则化和重整化的尝试。
(假设在小尺度上存在新的物理学,另见正则化从这个经典问题中去除无穷大的替代方法。)
在计算带电 Electric Charged粒子的电磁 electromagnetic相互作用时,人们很容易忽略粒子自身的场对自己的反作用 Back-reaction。(类似于电路分析的反电动势 Back-EMF)。但是这种反作用对于解释带电粒子发射辐射时的摩擦是必要的。如果假设电子是一个点,反作用的值就会发散,这和质量发散的原因是一样的,因为场是呈平方反比 Inverse-square的。
亚伯拉罕-洛伦兹理论有一个非因果的“预加速度”。有时,电子在施加力之前就开始移动了。这是点极限不一致的标志。
这个问题在经典场论中比在量子场论中更严重,因为在量子场论中,由于虚粒子-反粒子对的干涉,带电粒子经历了 Zitterbewegung,从而有效地抹去了一个可以与康普顿波长相比的区域上的电荷。在小耦合的量子电动力学中,电磁质量只随着粒子半径的对数发散。
量子电动力学中的发散
在20世纪30年代发展量子电动力学时,马克斯·伯恩、维尔纳·海森堡、帕斯夸尔·乔丹和保罗·狄拉克发现,在微扰修正中,许多积分是发散的(见无穷大问题)。
一种描述微扰理论修正发散的方法是由Hans Kramers[2],Hans Bethe[3] ,Julian Schwinger,[4][5][6][7]Richard Feynman[8][9][10]和Shin'ichiro Tomonaga,[11][12][13][14][15][16][17] and systematized Freeman Dyson in 1949.[18]在1947-49年发现的,并在1949年被Freeman Dyson系统化。发散出现在含虚粒子闭环的费曼图的辐射校正中。
虚粒子遵循能量和动量守恒,它们可以有任何能量和动量,甚至是观测到的粒子质量的相对能量和动量关系所不允许的能量和动量(即,[math]\displaystyle{ E^2 - p^2 }[/math]不一定是这个过程中粒子质量的平方,例如,对于光子它可能是非零的)。这样的粒子叫做离壳粒子。当有一个圈时,参与圈的粒子的动量不是唯一由入射和输出粒子的能量和动量决定的。圈中一个粒子能量的变化可以被圈中另一个粒子能量相等而相反的变化所平衡,而不影响进入和流出的粒子。因此,有许多变化是可能的。因此,为了找到圈过程的振幅,必须对所有可能的能量和动量的组合进行积分,这些组合可能在圈中传播。
这些积分通常是发散的,也就是说,它们给出无限的结果。其中“紫外”发散较为显著。紫外发散来自于以下几种情形:
- 所有圈中粒子具有很大的能量和动量的积分区域;
- 在场的路径积分中,场具有非常短的波长和高频涨落;
- 如果这个圈是粒子路径的和,粒子发射和吸收之间的固有时间很短。
所以这些发散是短距离,短时间的现象。
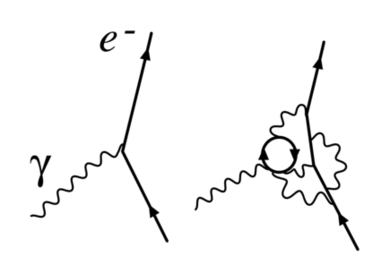
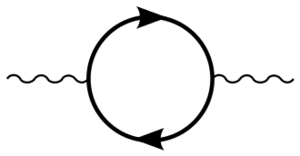
如右图所示。量子电动力学中有三个单圈发散圈图:[19]
- (a)一个光子产生一个虚拟电子-正电子对,然后这个电子-正电子对湮灭。这是真空极化图。
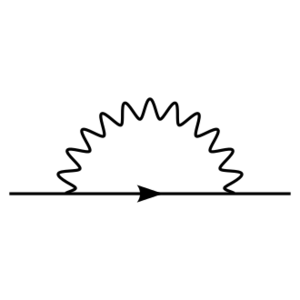
- (b)电子迅速发射并重新吸收虚光子,称为自能。
- (c)电子发射一个光子,发射第二个光子,并重新吸收第一个光子。这个过程如下面的图2所示,它被称为顶点重正化。费曼图也被称为“企鹅图”,因为它的形状很像企鹅。
这三中发散对应于所考虑理论中的三个参数:
- 场归一化因子Z
- 电子的质量
- 电子的电荷
第二类发散称为红外发散,由无质量粒子造成的,比如光子。每一个涉及带电粒子的过程都会发射出无限多个波长无限的相干光子,而发射任意有限数量光子的振幅为零。对于光子来说,这些发散过程研究透彻,理解清晰。例如在单圈阶处,顶点函数既有紫外散度也有红外散度。与紫外发散相反,红外发散在理论中不需要参数的重整化。顶点图的红外散度通过包含一个类似于顶点图的图来消除,该图具有以下重要的特征:连接电子(两条腿)的光子被切断并被两个波长趋向于无穷大的在壳(实)光子所取代;该图图相当于轫致辐射过程。该图被包含在内是必要的,因为没有物理方法来区分在顶点图中流过圈的零能量光子和通过轫致辐射发射的零能量光子。从数学的角度来看,红外发散可以通过假设对参数进行分数阶微分来正则化,例如:
- [math]\displaystyle{ \left( p^2 - a^2 \right)^{\frac{1}{2}} }[/math]
式1在p = a处定义良好,不过却是紫外散度;如果我们对−a2求3/2阶导数,就可以得到红外散度:
- [math]\displaystyle{ \frac{1}{p^2 - a^2}, }[/math]
因此我们可以通过将红外发散转化为紫外发散对其进行修正。
单圈发散
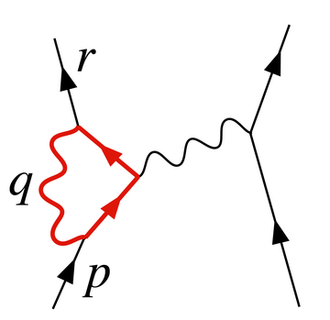
图2中的图式显示了量子电动力学中单圈对电子-电子散射的贡献之一。图左侧的电子,用实线表示,开始时是4动量的pμ,结束时是4动量的rμ。它发射一个携带rμ − pμ的虚光子,将能量和动量传递给另一个电子。但在这张图中,在这之前,它发射了另一个4动量的qμ的虚光子,它在发射了另一个虚光子后重新吸收了这个。能量和动量守恒并不能唯一地决定4动量qμ,所以所有的可能性都是相等的,我们必须积分。
除去其他因素,该图的振幅最终成为下圈的一个因子:
- [math]\displaystyle{ -ie^3 \int \frac{d^4 q}{(2\pi)^4} \gamma^\mu \frac{i (\gamma^\alpha (r - q)_\alpha + m)}{(r - q)^2 - m^2 + i \epsilon} \gamma^\rho \frac{i (\gamma^\beta (p - q)_\beta + m)}{(p - q)^2 - m^2 + i \epsilon} \gamma^\nu \frac{-i g_{\mu\nu}}{q^2 + i\epsilon}. }[/math]
这个表达式中的各种γμ因子是和狄拉克方程的协变公式一样的伽马矩阵; 它们与电子的自旋有关。e的因子为电耦合常数,提供了动量空间中绕极点积分轮廓的启发式定义。对于我们的目的来说,重要的部分是被积函数中三个主要因子对qμ的依赖,这三个因子来自圈中的两条电子线和光子线的传播子。
这是一个上面有两个qμ的幂的部分,在较大的qμ值时占优势(Pokorski 1987, p. 122):
- [math]\displaystyle{ e^3 \gamma^\mu \gamma^\alpha \gamma^\rho \gamma^\beta \gamma_\mu \int \frac{d^4 q}{(2\pi)^4} \frac{q_\alpha q_\beta}{(r - q)^2 (p - q)^2 q^2}. }[/math]
这个积分是发散且无限的,除非我们在能量和动量有限的时候截断它。
类似的环散度也出现在其他量子场论中。
重整化的裸量
解决方案是认识到最初出现在理论公式中的量(比如拉格朗日公式) ,代表着电子的电荷和质量以及量子场本身的归一化,实际上并不符合在实验室测量所得的物理常数。如上所述,它们是裸量,并没有考虑虚粒子环效应对物理常数本身的影响。在其他情况中,这些影响还包括让经典电磁学理论家为难的电磁反作用量子对应物。一般来说,这些效应最初就会像考虑中的振幅一样发散; 所以有限的测量量通常意味着发散裸量。
因此,为了与现实接轨,这些公式必须以可测量的、重整化的量进行重写。例如,电子的电荷可以用在特定运动学重整化点或减点测量的量来定义(这种定义下通常具有一个特征能量,称为重整化标度或简称为能量标度)。剩下的涉及剩余裸量的拉格朗日部分,可以被重新解释为包含在发散图中,且正好抵消其他图发散现象的反项。
量子电动力学中的重整化
例如,在量子电动力学的拉格朗日函数中
- [math]\displaystyle{ \mathcal{L}=\bar\psi_B\left[i\gamma_\mu \left (\partial^\mu + ie_BA_B^\mu \right )-m_B\right]\psi_B -\frac{1}{4}F_{B\mu\nu}F_B^{\mu\nu} }[/math]
磁场和耦合常数实际上是裸量,因此可见上面的下标如此B。通常,裸量相应的拉格朗日项是重整化项的倍数:
- [math]\displaystyle{ \left(\bar\psi m \psi\right)_B = Z_0 \bar\psi m \psi }[/math]
- [math]\displaystyle{ \left(\bar\psi\left(\partial^\mu + ieA^\mu \right )\psi\right)_B = Z_1 \bar\psi \left (\partial^\mu + ieA^\mu \right)\psi }[/math]
- [math]\displaystyle{ \left(F_{\mu\nu}F^{\mu\nu}\right)_B = Z_3\, F_{\mu\nu}F^{\mu\nu}. }[/math]
通过 Ward-Takahashi 恒等式规范不变性,证明了我们可以重整共变导数的两个项在一起
- [math]\displaystyle{ \bar \psi (\partial + ieA) \psi }[/math] (Pokorski 1987,第115页),
这实际上也是Z2所发生的; 与Z1相同。
拉格朗日函数中的一个项,例如图1所示的电子-光子相互作用,就可以被写出来
- [math]\displaystyle{ \mathcal{L}_I = -e \bar\psi \gamma_\mu A^\mu \psi - (Z_1 - 1) e \bar\psi \gamma_\mu A^\mu \psi }[/math]
这个物理常数e,即电子的电荷,可以用一些特定的实验来定义: 我们把重整化标度设置为与这个实验的能量特征相等,第一个项就会给出我们在实验室中看到的相互作用(只要提供诸如磁矩的高阶修正,从环形图中就可以得到小的、有限的修正)。剩下的就是反项了。如果理论是可重整化的(更多内容见下文) ,就像量子点动力学中一样,环路图的分叉部分都可以分解由成三个或更少分支组成的部分,并且其拥有可以被第二项(或者类似的从Z0 和Z3得到的反项)抵消的代数形式。
图3所示的反项的交互顶点Z1的图抵消了图2中环的发散。
从历史上看,将“裸项”分解为原始项和反项的做法,早于肯尼思 · 威尔逊对重整化群的洞察。[20]根据这些重整化群的洞察,在更细节的部分里这种分裂是非自然的也是非物理的,因为问题的所有尺度都是以连续的系统方式进入的。
运转联轴器
为了尽量减少环路图对给定计算的影响(从而使得计算结果更容易提取) ,可以选择一个接近相互作用中交换的能量和动量的重整化点。然而,重整化点本身并不是一个物理量: 在计算到所有的阶之下,理论物理的预测,原则上应该独立于重整化点的选择,只要它在理论的应用范围内。重整化尺度的变化将影响无环费曼图产生的结果多少,以及来自环图剩余的有限部分的结果的多少。人们可以利用这一事实来计算物理常数随规模变化的有效变化。这种变化由 β 函数编码,这种尺度依赖的一般理论被称为重整化群。
通俗地说,粒子物理学家经常说的某些物理“常数”随着相互作用的能量而变化,尽管事实上,重整化标度才是独立量。然而,这种运行确实提供了一种方便的手段来描述场理论在相互作用所涉及的能量变化下的行为变化。例如,由于量子色动力学中的耦合在大能量尺度下变小,该理论表现得更像一个自由理论,因为在相互作用中交换的能量变大了——这种现象被称为渐近自由。选择一个递增的能量尺度并使用重整化群,可以从简单的费曼图中清楚地看出这一点; 如果不这样做,预测结果将是一样的,但是会出现复杂的高阶抵消。
比如说,
- [math]\displaystyle{ I=\int_0^a \frac{1}{z}\,dz-\int_0^b \frac{1}{z}\,dz=\ln a-\ln b-\ln 0 +\ln 0 }[/math]
是不明确的。
为了去除发散,只需将积分的下限改为εa和εb:
- [math]\displaystyle{ I=\ln a-\ln b-\ln{\varepsilon_a}+\ln{\varepsilon_b} = \ln \tfrac{a}{b} - \ln \tfrac{\varepsilon_a}{\varepsilon_b} }[/math]
确保[math]\displaystyle{ \frac{\varepsilon_{b}}{\varepsilon_{a}} }[/math] → 1,然后[math]\displaystyle{ I=ln\frac{a}{b} }[/math]。
正则化
由于∞ − ∞的定义是不明确的,为了使散度抵消的概念更加精确,散度首先必须使用极限理论在数学上被驯服,这一过程被称为正则化(Weinberg, 1995)。
本质上任意修改圈被积函数,或调节器,可以使它们在高能量和动量下下降得更快,这样积分就会收敛。调节器有一个称为截止的特征能量标度;将这个截止值取为无穷大(或者,等价地,将相应的长度/时间标度取为零),就可以恢复原来的积分。
有了调节器,并且截止值是有限的,积分中的发散项就变成了有限的,且与截止相关的项。在用依赖截止的反项抵消这些项后,截止到无穷大,并恢复有限的物理结果。如果我们可以测量的标度上的物理现象与在最短距离和时间尺度上发生的事情无关,那么就有可能得到与截止无关的计算结果。
量子场论计算中使用了许多不同类型的调节器,它们各有优缺点。在现代应用中最流行的是由Gerardus 't Hooft和Martinus J. G. Veltman[21]发明的量纲正则化,它通过将积分带入一个虚构的分数维数的空间来驯服积分。另一种是保利-维拉斯正则化,它以非常大的质量将虚构的粒子添加到理论中,这样涉及大质量粒子的圈积分在大动量中抵消了现有的圈。
另一种正则化方案是肯尼斯·威尔逊(Kenneth Wilson)提出的晶格正则化,它假设超立方晶格以固定的网格大小构建我们的时空。这一网格大小是粒子在晶格上传播时所能拥有的最大动量的自然截止。在对几个网格大小不同的网格进行计算后,物理结果外推到网格大小为0的情况,或是我们的自然宇宙。这以标度极限的存在为先决条件。
重正化理论的一个严格的数学方法是因果摄动理论,其中紫外散度从计算的开始就可以避免,只需要在分布理论的框架内进行定义良好的数学运算。在这种方法中,散度可以由模糊度代替:这个对应于散度图的术语是一个有限的,但未确定的系数。之后其他原理,如规范对称,必须用来减少或消除模糊度。
Zeta函数正则化
朱利安·施温格使用渐近关系作为调节器(其中Λ → ∞):
- [math]\displaystyle{ I(n, \Lambda )= \int_0^{\Lambda }dp\,p^n \sim 1+2^n+3^n+\cdots+ \Lambda^n \to \zeta(-n) }[/math]
发现了Λ → ∞函数正则化重整化之间的联系。在此基础上,他考虑利用ζ(−n)的值来得到有限的结果。尽管他得出的结果不一致,但是由Hartle, J. Garcia研究的改进公式,并基于E. Elizalde的工作,依然囊括了zeta正则化算法的技术
- [math]\displaystyle{ I(n, \Lambda) = \frac{n}{2}I(n-1, \Lambda) + \zeta(-n) - \sum_{r=1}^{\infty}\frac{B_{2r}}{(2r)!} a_{n,r}(n-2r+1) I(n-2r, \Lambda), }[/math]
其中B代表伯努利数,并且
- [math]\displaystyle{ a_{n,r}= \frac{\Gamma(n+1)}{\Gamma(n-2r+2)}. }[/math]
所以每个I(m, Λ)都可以写成ζ(−1), ζ(−3), ζ(−5), ..., ζ(−m)。
或者简单地对每一个发散积分使用阿贝尔-普拉纳公式:
- [math]\displaystyle{ \zeta(-m, \beta )-\frac{\beta ^{m}}{2}-i\int_ 0 ^{\infty}dt \frac{ (it+\beta)^{m}-(-it+\beta)^{m}}{e^{2 \pi t}-1}=\int_0^\infty dp \, (p+\beta)^m }[/math]
当m > 0时成立,这里的Zeta函数是赫尔维茨函数,其中β是一个正实数。
“几何”的类比由下式给出,(如果我们使用矩形法)来计算积分:
- [math]\displaystyle{ \int_0^\infty dx \, (\beta +x)^m \approx \sum_{n=0}^\infty h^{m+1} \zeta \left( \beta h^{-1} , -m \right) }[/math]
使用赫尔维茨Zeta正则化加上步骤h的矩形法(此处h不要与普朗克常数混淆)。
对数发散积分具有正则化
- [math]\displaystyle{ \sum_{n=0}^{\infty} \frac{1}{n+a}= - \psi (a)+\log (a) }[/math]
因为对于调和级数[math]\displaystyle{ \sum_{n=0}^{\infty} \frac{1}{an+1} }[/math]在a趋近于零处,我们必须恢复级数[math]\displaystyle{ \sum_{n=0}^{\infty}1 =1/2 }[/math]
对于依赖于多个变量[math]\displaystyle{ k_1, \cdots, k_n }[/math]的多圈积分,我们可以将变量转换为极坐标,然后用一个和替换角度上的积分[math]\displaystyle{ \int d \Omega }[/math],因此我们只有一个发散积分,它取决于模[math]\displaystyle{ r^2 = k_1^2 +\cdots+k_n^2 }[/math],然后我们可以应用Zeta正则化算法,多圈积分的主要思想是将因子[math]\displaystyle{ F(q_1,\cdots,q_n) }[/math]替换为超球坐标F(r, Ω),使紫外重叠散度编码在变量r中。为了正则化这些积分,需要一个调节器,对于多圈积分的情况,这些调节器可以被视为:
- [math]\displaystyle{ \left (1+ \sqrt{q}_{i}q^{i} \right )^{-s} }[/math]
所以多圈积分在足够大的s时收敛,使用正则化我们可以继续分析变量s直到s = 0的物理极限,然后正则化任何紫外积分,通过用发散级数的线性组合替换发散积分,它可以正则化为黎曼ζ函数的负值ζ(−m)。
态度以及解读
量子电动力学和其他量子场论的早期规范者通常对这种(重整化的)处理方式不满意。为了得到有限的答案而从无限中减去无限,这似乎是不合理的。
弗里曼戴森认为,这些无穷大是一个自然的基本性质,不能被任何形式的数学程序所消除,比如重整化方法。[22][23]
狄拉克的批评是最持久的。[24]直到1975年,他仍表示:[25]
- “大多数物理学家对这种情况非常满意。他们说: ‘量子电动力学理论是一个很好的理论,我们再也不用担心它了’。但我必须说,我对这种情况非常不满意,因为这种所谓的“好理论”确实有涉及忽视方程式中出现的无穷大,且以一种武断的方式忽视它们。这根本不是合理的数学。合理的数学涉及对微小量的忽略,而不是仅仅因为一个量无限大,你不想要它就可以忽略它!”
另一位重要的评论家是费曼。尽管他在量子电动力学的发展中扮演了关键角色,他在1985年写道:[26]
- “我们玩的这个骗局在技术上叫做“重整化”。但是不管这个词多么聪明,它仍然是我所说的一个含糊的过程!不得不求助于这样的骗术阻碍了我们证明量子电动力学理论在数学上是自洽的脚步。令人惊讶的是,到目前为止,这个理论仍然没有以这样或那样的方式被证明是自洽的; 我怀疑重整化在数学上是不正当的。”
费曼担心,在20世纪60年代所有已知的场理论都有这样的特性: 在足够短的距离尺度上,相互作用会变得无限强。这个性质被称为Landau pole,它使量子场理论完全不一致的说法变得可信。1974年,Gross,Politzer 和 Wilczek 证明了另一个量子场论(即量子色动力学),并没有Landau pole。费曼和其他大多数人一样,承认量子色动力学是一个完全一致的理论。
直到20世纪70年代和80年代,这种普遍的不安在文献中几乎是普遍存在的。然而,从20世纪70年代开始,尽管狄拉克和其他各种人---- 那些老一辈的理论家---- 从未收回他们的批评,受到重整化群理论和有效场理论工作的启发,人们的态度开始改变,尤其是在年轻的理论家中。肯尼斯·威尔森和其他人证明了重整化群对凝聚态物理学中统计场理论的应用有帮助,因为它对相变行为提供了重要的见解。在凝聚态物理学,存在一个物理的短距离调节器:在原子规模下,物质不再是连续的。凝聚态物理学中的短距离发散并不构成哲学问题,因为场论实际也只是对物质行为的一种有效的、平滑的理想表示; 因为截止值总是有限的,所以没有无限性,而且裸量依赖于截止值也是完全合理的。
如果量子场论能一直保持成立到普朗克长度以下(在那里它可能会产生弦论、因果集合论或其他不同的理论) ,那么粒子物理学中的短距离发散可能也不存在实质的问题; 所有场论都可能是有效场论。在某种意义上,这种方法呼应了以前的态度,即量子力学中的发散说明了人类对自然运作规律的无知,但也承认这种无知是可以量化的,且由此产生的有效理论仍然是有用的。
尽管如此,萨拉姆在1972年的言论似乎仍然有意义:
- 场论的无穷大首次出现在洛伦兹对电子自质量的计算过程中,它在经典电动力学中已经存在了七十年,在量子电动力学中也已存在了35年。这么多年的挫折使得研究这个课题的人对无穷大产生了一种奇怪的感情,并且热切地相信它们是自然界不可避免的一部分; 以至于即使他们有可能避开了正解,有限的重整化常数可被计算--这样的希望都被认为是不合理的。将罗素的附言与他的自传《最后的岁月,1944-1969》(乔治 · 艾伦和安文出版社,伦敦,1969年)的第三卷相比较,在第221页:
- “在现代社会,如果团体不幸福,那往往是因为他们有那些比幸福甚至生命更重要的无知、习惯、信仰和激情。我发现在我们这个危险的时代,有许多人似乎爱上了痛苦和死亡,以至于当面对希望时,他们会生气起来。他们认为希望是非理性的,坐下来懒洋洋地绝望只是在面对事实而已。”
在量子场论中,一个物理常数的值,一般来说,取决于我们选择的重整化点的尺度,在能量尺度变化的情况下,研究重整化群物理常数的运行变得非常有趣。粒子物理标准模型中的耦合常数随着能量的增加而以不同的方式变化: 量子色动力学的耦合和电弱力的弱同位旋耦合趋于减小,电弱力的弱超荷耦合趋于增加。在1015 GeV 的巨大能量尺度内(远远超出我们现有的粒子加速器的能量范围) ,它们都变得大致相同(Grotz 和 Klapdor 1990,p. 254) ,这是推测大统一理论的主要动机。重整化已经不再是一个令人担忧的问题,而是成为研究不同区域中场理论行为的一个重要理论工具。
如果一个具有重整化特征的理论(例如:量子电动力学(QED))只能合理地被解释为一种有效场理论,即作为反映人类对自然规律的无知的近似反应,那么问题仍在于发现一个更精确的,不存在这些重整化问题的理论。正如路易斯 · 莱德所说,“在量子理论中,这些[经典]发散并没有消失; 相反,它们似乎变得更糟。尽管重整化理论相对成功,但人们仍然认为,应该有一种更令人满意的处理方法。”[27]
可重整性
从这一哲学的重新评价中,一个新的概念自然地产生了:即可重整性。不是所有的理论都能以上述的方式重整化,且在计算结束时,有限的反项和所有的量变得截止无关。如果拉格朗日算子包含能量单位足够高维的场算符组合,抵消所有散度所需要的反项激增到无穷多个。乍一看这个理论似乎获得了无数的自由参数,然而却因此失去了所有的预测能力,也就在科学上变得毫无价值。这样的理论被称为不可重整的理论。
粒子物理的标准模型只包含可重整算子,但如果有人试图以最直接的方式构建量子引力场理论(将爱因斯坦-希尔伯特拉格朗日公式中的度规视为对闵可夫斯基度规的扰动),广义相对论的相互作用就会成为不可重整化的算子,这表明微扰理论在量子引力中的应用并不令人满意。
然而,在有效场理论中,严格来说,“重整化性”是一个误称。在非重整有效场理论中,拉格朗日算子的各项确实可以增加到无穷,但系数会被越来越极端的能量截止逆幂所抑制。如果截止是一个真实的物理量,也就是说,如果这个理论仅仅是对某些最大能量或最小距离尺度下的物理的有效描述,那么这些额外的项就可以代表真实的物理相互作用。假设理论中的无量纲常数不会变得太大,我们可以通过截止的逆幂来分组计算,在包含有限数量自由参数的截止中提取有限阶的近似预测。甚至可以对这些“不可重整化”的交互进行重整化。
在有效场论中,当能量尺度比截止小得多时,非重整相互作用迅速变弱。经典例子是弱核力的费米理论,这是一种非重整有效理论,其截止可与W粒子的质量相当。这一事实也提供了一种可能的解释—为什么我们看到几乎所有粒子相互作用都可以用重整化理论来描述。可能存在于统一场论或普朗克尺度上的任何其他物质在我们能观测到的领域中都变得太弱了。只有一个例外:引力,它极其微弱的相互作用被巨大质量的恒星和行星的存在放大了。
重整化方案
在实际计算中,为了抵消费曼图计算中超出树图的散度而引入的反项必须使用一组重整化条件来解决。常用的重整化方案包括:
- 最小减法(MS)方案和相关的改进最小减法(MS-bar)方案;
- 在壳方案
重整化在统计物理中的应用
历史
凝聚态物理学对重整化过程的物理意义和推广提供了更深入的理解,它超越了传统重整化理论的膨胀群。Leo P. Kadanoff在1966年的论文中提出了“块区自旋”重整群。[28]分块思想是一种将理论中远距离的分量定义为较短距离分量的集合的方法。
这种方法涵盖了概念,另外Kenneth Wilson在他的大量杰出工作中给出了完整的计算内容[20]。威尔逊思想的力量在1974年通过对一个长期存在的问题——近藤问题(或称康多问题),的建设性迭代重整化解决方案得到了证明,在此之前,他的新方法在1971年的二阶相变理论和临界现象的开创性发展也得到了证明。1982年,鉴于威尔逊杰出的贡献,他被授予诺贝尔奖。
这种方法涵盖了概念点,并给出了充分的计算实质。
原理
更专业地来说,让我们假设我们有一个由状态变量[math]\displaystyle{ \{s_i\} }[/math]和耦合常数[math]\displaystyle{ \{J_k\} }[/math]的某个函数[math]\displaystyle{ Z }[/math]描述的理论。这个函数可以是配分函数、作用函数、哈密顿函数等等。它必须包含整个系统的物理描述。
现在我们考虑状态变量[math]\displaystyle{ \{s_i\} }[/math]到[math]\displaystyle{ \{\tilde s_i\} }[/math]的某种分块变换,[math]\displaystyle{ \tilde s_i }[/math]的数目必须小于[math]\displaystyle{ s_i }[/math]的数目。现在让我们尝试仅根据[math]\displaystyle{ s_i }[/math]来重写[math]\displaystyle{ Z }[/math]函数。如果这可以通过参数的某种变化实现,则[math]\displaystyle{ \{J_k\} }[/math]改为[math]\displaystyle{ \{\tilde J_k\} }[/math],则该理论是可重整化的。
系统在大尺度上可能的宏观状态是由这组固定点给出的。
重整化群的固定点
重整化群流中最重要的内容是它的固定点。固定点是由与流相关的β函数的消失来定义的。然后根据定义,重整化群的固定点是标度不变的。在许多物理领域内,标度不变性扩大为正形不变性。然后在固定点处符合共形场论。
几种理论都可以流动到同一固定点的性质产生了普遍性。如果这些固定点与自由场论相对应,那么这个理论就表现出了量子的平凡性。在格子希格斯理论的研究中出现了许多固定点,但与之相关的量子场论的本质仍然是一个悬而未决的问题。[29]
参见
- History of quantum field theory
- Quantum triviality
- Zeno's paradoxes
参考文献
- ↑ See e.g., Weinberg vol I, chapter 10.
- ↑ Kramers presented his work at the 1947 Shelter Island Conference, repeated in 1948 at the Solvay Conference. The latter did not appear in print until the Proceedings of the Solvay Conference, published in 1950 (see Laurie M. Brown (ed.), Renormalization: From Lorentz to Landau (and Beyond), Springer, 2012, p. 53). Kramers' approach was nonrelativistic(see Jagdish Mehra, Helmut Rechenberg, The Conceptual Completion and Extensions of Quantum Mechanics 1932-1941. Epilogue: Aspects of the Further Development of Quantum Theory 1942-1999: Volumes 6, Part 2, Springer, 2001, p. 1050).
- ↑ H. Bethe (1947). "The Electromagnetic Shift of Energy Levels". Physical Review. 72 (4): 339–341. Bibcode:1947PhRv...72..339B. doi:10.1103/PhysRev.72.339.
- ↑ Schwinger, J. (1948). "On quantum-electrodynamics and the magnetic moment of the electron". Physical Review. 73 (4): 416–417. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
- ↑ Schwinger, J. (1948). "I. A covariant formulation". Physical Review. Quantum Electrodynamics. 74 (10): 1439–1461. Bibcode:1948PhRv...74.1439S. doi:10.1103/PhysRev.74.1439.
- ↑ Schwinger, J. (1949). "II. Vacuum polarization and self-energy". Physical Review. Quantum Electrodynamics. 75 (4): 651–679. Bibcode:1949PhRv...75..651S. doi:10.1103/PhysRev.75.651.
- ↑ Schwinger, J. (1949). "III. The electromagnetic properties of the electron radiative corrections to scattering". Physical Review. Quantum Electrodynamics. 76 (6): 790–817. Bibcode:1949PhRv...76..790S. doi:10.1103/PhysRev.76.790.
- ↑ Feynman, Richard P. (1948). "Space-time approach to non-relativistic quantum mechanics" (PDF). Reviews of Modern Physics. 20 (2): 367–387. Bibcode:1948RvMP...20..367F. doi:10.1103/RevModPhys.20.367.
- ↑ Feynman, Richard P. (1948). "A relativistic cut-off for classical electrodynamics" (PDF). Physical Review. 74 (8): 939–946. Bibcode:1948PhRv...74..939F. doi:10.1103/PhysRev.74.939.
- ↑ Feynman, Richard P. (1948). "A relativistic cut-off for quantum electrodynamics" (PDF). Physical Review. 74 (10): 1430–1438. Bibcode:1948PhRv...74.1430F. doi:10.1103/PhysRev.74.1430.
- ↑ Tomonaga, S. (1946-08-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields". Progress of Theoretical Physics. Oxford University Press (OUP). 1 (2): 27–42. Bibcode:1946PThPh...1...27T. doi:10.1143/ptp.1.27. ISSN 1347-4081.
- ↑ Koba, Z.; Tati, T.; Tomonaga, S.-i. (1947-10-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. II: Case of Interacting Electromagnetic and Electron Fields". Progress of Theoretical Physics. Oxford University Press (OUP). 2 (3): 101–116. Bibcode:1947PThPh...2..101K. doi:10.1143/ptp/2.3.101. ISSN 0033-068X.
- ↑ Koba, Z.; Tati, T.; Tomonaga, S.-i. (1947-12-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. III: Case of Interacting Electromagnetic and Electron Fields". Progress of Theoretical Physics. Oxford University Press (OUP). 2 (4): 198–208. Bibcode:1947PThPh...2..198K. doi:10.1143/ptp/2.4.198. ISSN 0033-068X.
- ↑ Kanesawa, S.; Tomonaga, S.-i. (1948-03-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields. [IV]: Case of Interacting Electromagnetic and Meson Fields". Progress of Theoretical Physics. Oxford University Press (OUP). 3 (1): 1–13. doi:10.1143/ptp/3.1.1. ISSN 0033-068X.
- ↑ Kanesawa, S.; Tomonaga, S.-i. (1948-06-01). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields V: Case of Interacting Electromagnetic and Meson Fields". Progress of Theoretical Physics. Oxford University Press (OUP). 3 (2): 101–113. Bibcode:1948PThPh...3..101K. doi:10.1143/ptp/3.2.101. ISSN 0033-068X.
- ↑ Koba, Z.; Tomonaga, S.-i. (1948-09-01). "On Radiation Reactions in Collision Processes. I: Application of the "Self-Consistent" Subtraction Method to the Elastic Scattering of an Electron". Progress of Theoretical Physics. Oxford University Press (OUP). 3 (3): 290–303. Bibcode:1948PThPh...3..290K. doi:10.1143/ptp/3.3.290. ISSN 0033-068X.
- ↑ Tomonaga, Sin-Itiro; Oppenheimer, J. R. (1948-07-15). "On Infinite Field Reactions in Quantum Field Theory". Physical Review. American Physical Society (APS). 74 (2): 224–225. Bibcode:1948PhRv...74..224T. doi:10.1103/physrev.74.224. ISSN 0031-899X.
- ↑ Dyson, F. J. (1949). "The radiation theories of Tomonaga, Schwinger, and Feynman". Phys. Rev. 75 (3): 486–502. Bibcode:1949PhRv...75..486D. doi:10.1103/PhysRev.75.486.
- ↑ Peskin, Michael E.; Schroeder, Daniel V. (1995). An Introduction to Quantum Field Theory. Reading: Addison-Wesley. Chapter 10. https://archive.org/details/introductiontoqu0000pesk.
- ↑ 20.0 20.1 Wilson, Kenneth G. (1975-10-01). "The renormalization group: Critical phenomena and the Kondo problem". Reviews of Modern Physics. American Physical Society (APS). 47 (4): 773–840. Bibcode:1975RvMP...47..773W. doi:10.1103/revmodphys.47.773. ISSN 0034-6861.
- ↑ 't Hooft, G.; Veltman, M. (1972). "Regularization and renormalization of gauge fields". Nuclear Physics B. 44 (1): 189–213. Bibcode:1972NuPhB..44..189T. doi:10.1016/0550-3213(72)90279-9. hdl:1874/4845.
- ↑ Dyson, F. J. (1952-02-15). "Divergence of Perturbation Theory in Quantum Electrodynamics". Physical Review. American Physical Society (APS). 85 (4): 631–632. Bibcode:1952PhRv...85..631D. doi:10.1103/physrev.85.631. ISSN 0031-899X.
- ↑ Stern, A. W. (1952-11-07). "Space, Field, and Ether in Contemporary Physics". Science. American Association for the Advancement of Science (AAAS). 116 (3019): 493–496. Bibcode:1952Sci...116..493S. doi:10.1126/science.116.3019.493. ISSN 0036-8075. PMID 17801299.
- ↑ P.A.M. Dirac, "The Evolution of the Physicist's Picture of Nature," in Scientific American, May 1963, p. 53.
- ↑ Kragh, Helge; Dirac: A scientific biography, CUP 1990, p. 184
- ↑ Feynman, Richard P.; QED: The Strange Theory of Light and Matter, Penguin 1990, p. 128
- ↑ Ryder, Lewis. Quantum Field Theory, page 390 (Cambridge University Press 1996).
- ↑ Leo Kadanoff|L.P. Kadanoff (1966): "Scaling laws for Ising models near [math]\displaystyle{ T_c }[/math]", Physics (Long Island City, N.Y.) 2, 263.
- ↑ "Triviality Pursuit: Can Elementary Scalar Particles Exist?". Physics Reports. 167 (5): 241–320. 1988. Bibcode:1988PhR...167..241C. doi:10.1016/0370-1573(88)90008-7.
拓展阅读
概述
- DeDeo, Simon; Introduction to Renormalization (2017). Santa Fe Institute Complexity Explorer MOOC. Renormalization from a complex systems point of view, including Markov Chains, Cellular Automata, the real space Ising model, the Krohn-Rhodes Theorem, QED, and rate distortion theory.
- Delamotte, Bertrand (2004). "A hint of renormalization". American Journal of Physics. 72 (2): 170–184. arXiv:hep-th/0212049. Bibcode:2004AmJPh..72..170D. doi:10.1119/1.1624112.
- Baez, John; Renormalization Made Easy, (2005). A qualitative introduction to the subject.
- Blechman, Andrew E.; Renormalization: Our Greatly Misunderstood Friend, (2002). Summary of a lecture; has more information about specific regularization and divergence-subtraction schemes.
- Cao, Tian Yu; Schweber, Silvan S. (1993). "The conceptual foundations and the philosophical aspects of renormalization theory". Synthese. 97: 33–108. doi:10.1007/BF01255832.
- Shirkov, Dmitry; Fifty Years of the Renormalization Group, C.E.R.N. Courrier 41(7) (2001). Full text available at : I.O.P Magazines.
编者推荐
集智文章
在没有任何先验信息的情况,能不能利用机器学习的方法,学会某种“窥一斑而知全豹”的方法,找到那些适当的自由度来进行后续的重整化操作呢?近期发表在 Nature 的一篇论文讨论了这一问题,东京大学博士后、南京大学物理学博士傅渥成对这篇论文进行了解读。
从基本粒子到原子、光波、水波,自然似乎倾向于将自己分裂成不同尺度的独立世界,而重整化的过程则将小尺度与大尺度联系起来。有物理学家认为,重整化可以说是过去50年理论物理学中最重要的进展。在亚原子物理学中,重整化告诉我们,何时可以只处理相对简单的质子,而忽略掉其内部彼此纠缠的夸克。不过,当问题简化之后,那些忽略掉的微观细节要如何看到呢?(图4)
尤亦庄:深度学习和重整化群(图5) | 因果涌现读书会第二期
什么是重整化技术?重整化技术的发展脉络和最新进展是什么?重整化技术与当前的深度学习技术有什么关联?如何借助重整化技术来解决当前深度学习中面临的一些问题。加州大学圣地亚哥分校助理教授尤亦庄将带你共同梳理关于重整化技术的一些进展。
因复杂物理系统的分析取决于从众多其他自由度中提取相关自由度的能力。尽管人们对机器学习寄予厚望,但它也带来了可解释性的挑战。研究人员通常不清楚学习到的“相关”特征与物理理论的对应关系。在最近发表在 Physics Review Letters 的一篇文章中,研究人员报告了有助于解决这个问题的理论结果:他们建立了重整化群的场论相关性与信息瓶颈(information bottleneck,IB)理论定义的相关性概念之间的等价性。他们的分析表明,对于由场论描述的统计物理系统,使用IB理论发现的自由度确实对应于具有最低标度维数的算子。他们以数值方式证实了他们的场论预测。研究人员研究了IB算法对物理对称性的依赖性。他们的发现提供了一个连接两个不同理论的方法,以及一个在物理的深度学习应用中能够给出物理可解释性的例子。
集智课程
本课程讲师为陈晓松(图6)。
在理论物理中,重整化群(renormalization group,简称RG)是一个在不同长度标度下考察物理系统变化的数学工具。标度上的变化称为“标度变换”。重整化群与“标度不变性”和“共形不变性”的关系较为紧密。共形不变性包含了标度变换,它们都与自相似有关。在重整化理论中,系统在某一个标度上自相似于一个更小的标度,但描述它们组成的参量值不相同。系统的组成可以是原子,基本粒子,自旋等。系统的变量是以系统组成之间的相互作用来描述。
本课程中,主要讲解了重整化群理论的历史发展与Wilson 提出此理论的关键点。
加州大学圣地亚哥分校助理教授尤亦庄将带你共同梳理关于重整化技术的一些历史脉络和进展,带你一窥重整化技术的本质,本次分享主要围绕以下内容开展: 1. 重整化理论的历史、现状与未来 2. 以Ising模型为例介绍机器学习重整化 3. 重整化方案的设计原则 4. 全息重整化及应用。
深度学习技术,尤其是生成模型在图像问题处理上大放异彩。 而生成模型之所以展现出强大的多层信号处理能力,与物理学中的重整化群理论密切相关。研究者结合重整化群方法和流模型,开发出可以发现自然作用力的AI“物理学家”,以及具有高可解释性与可控性的计算机视觉生成模型。相关研究发表在 Physical Review Research、Physical Review Letters 等期刊上,本文是对该研究方向的介绍。
本中文词条由白开水、Moonscar参与编译和审校,糖糖编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。