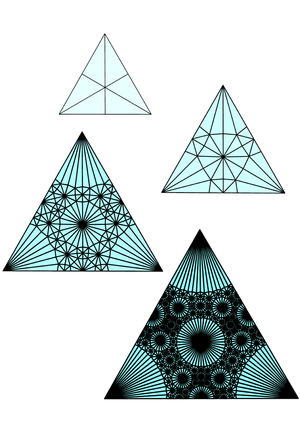
自相似

自相似一词由伯努瓦·曼德布洛特 Benoit Mandelbrot与1964年引入。[2]在数学中,一个自相似的物体与它自身的某一部分完全或近似地相似(例如:整体和一个或多个部分具有相同的形状)。现实世界中的许多物体,例如海岸线,在统计学上是自相似的:它们的某些部分在许多不同尺度上表现出相同的统计特性。[3] 自相似是分形的一个典型性质。标度不变性是自相似的一种精确形式:在任何放大倍数下,物体中总有更小的部分与整体相似。例如,科赫雪花的一边既对称又具有标度不变性;它可以连续放大3倍而不改变形状。分形中明显的非平凡的相似性是通过它们的精细结构或任意小尺度上的细节来区分的。对比一个反例来看,尽管直线的任何部分都可能类似于整体,但是进一步放大之后,却没有更多的细节显露。
对于一个依赖时间发展的现象,如果其相关观测量[math]\displaystyle{ f(x,t) }[/math]在不同时间所测得的数值不同,但是对应的无量纲量在给定的[math]\displaystyle{ x/t^z }[/math]下保持不变,则可以说该现象具有自相似性。通常如果[math]\displaystyle{ f(x,t) }[/math]显示出Dynamic Scaling 动态缩放就会出现这种情况。这也是相似三角形概念的拓展和延伸。[4][5][6]值得注意的是,即使两个三角形的边长不同,但他们的内角相等,则他们也是相似的。
佩特根 Peitgen等人曾这样解释这一概念:
如果一个图形的部分是整体的小尺度复制品,就可以认为这一图形是自相似的;如果图形分解产生的部分都是该图形的精确复制,则这个图形是严格自相似的。任何任意的部分都包含整个图形的精确复制。
即使从数学上来说,分形可以在无限放大的条件下显示出自相似性,但是这在物理上是不可能实现的。佩特根等建议使用近似方法来研究自相似性:
为了使自相似的性质具有操作意义,我们必须处理有限图形的有限近似。这可以采取盒子自相似性方法来解决,即使用不同尺寸的格子对图形的有限阶段进行测量。
自仿射性

在数学中,自仿射性 Self-affinity 是分形的特征之一,分形的各部分在 x 方向和 y 方向上按不同的比例缩放。这意味着要理解这些分形对象的自相似性,必须使用各向异性仿射变换 Anisotropic Affine Transformation 进行缩放。
定义
如果存在一个有限集 S 对[math]\displaystyle{ \{ f_s : s\in S \} }[/math]中的一组非满射同胚集 Non-surjective Homeomorphisms 进行索引,则紧致拓扑空间 Compact Topological Space X 是自相似的,有:
[math]\displaystyle{ X=\bigcup_{s\in S} f_s(X) }[/math]
假设有[math]\displaystyle{ X\subset Y }[/math],当且仅当X是Y'的唯一非空子集,使得上式对[math]\displaystyle{ \{ f_s : s\in S \} }[/math]成立,则X是自相似的。而且我们称[math]\displaystyle{ \mathfrak{L}=(X,S,\{ f_s : s\in S \} ) }[/math]是自相似结构。
同胚可以迭代,产生迭代函数系统 Iterated Function System 。函数的组合产生了幺半群 Monoid 的代数结构。当集合S只有两个元素时,幺半群此时称为二元幺半群 Dyadic Monoid。二元幺半群可以表示为无限二叉树;更一般地说,如果集合S有p个元素,则一元类可以表示为p进树 P-adic Tree 。
二元幺半群的自同构是模群 Modular Group ,自同构可以描述为二叉树的双曲旋转 Hyperbolic Rotations 。
比自相似性更一般的概念是自仿射性。
实例
曼德布洛特集在Misiurewicz 点附近也具有自相似性。
自相似对于计算机网络的设计有着重要的意义,因为典型的网络流量具有自相似的特性。[2]例如,在电信流量工程中,分组交换数据流量模式似乎在统计上是自相似的[2]。这种性质意味着使用Poisson Distribution 泊松分布的简单模型是不准确的,而没有考虑自相似性的网络很可能以意想不到的方式运行。
类似地,人们在描述股票市场时认为其波动具有自仿射性,也就是说,当根据显示的细节程度,通过适当的仿射变换进行转换时,它们显示出自相似性[9]。Andrew Lo描述了计量经济学中股票市场的对数回报自相似性[10]。
有限细分规则是一种建立自相似集的强大方法,包括 Cantor Set 康托集和谢尔宾斯基三角。
控制论领域
斯塔福德 · 比尔的可行系统模型是一个具有仿射自相似层次结构的组织模型,其中一个给定的可行系统是一个递归更高一级的可行系统之一的一个元素,对于这个系统的元素是一个递归层次更低的可行系统。
自然界中
自然中也存在自相似性。右边是一个数学生成的,完全自相似的蕨类图像,与自然蕨类有明显的相似之处。其他植物,如罗马花椰菜,表现出强烈的自相似性。
音乐世界
- 严格的经典表现出各种类型和数量的自相似性,赋格曲部分也是如此。
- 谢帕德音调在频率域或波长域是自相似的。
- 丹麦作曲家Per Nørgård在他的很多音乐中都使用了一种名为“无限系列”的自相似整数序列。
另见
参考文献
- ↑ Mandelbrot, Benoit B. (1982). The Fractal Geometry of Nature, p.44. .
- ↑ 2.0 2.1 2.2 Leland, W.E.; Taqqu, M.S.; et al. (January 1995). "On the self-similar nature of Ethernet traffic (extended version)" (PDF). IEEE/ACM Transactions on Networking. 2 (1): 1–15. doi:10.1109/90.282603.
- ↑ Mandelbrot, Benoit B. (5 May 1967). "How long is the coast of Britain? Statistical self-similarity and fractional dimension". Science. New Series. 156 (3775): 636–638. Bibcode:1967Sci...156..636M. doi:10.1126/science.156.3775.636. PMID 17837158. PDF
- ↑ Hassan M. K., Hassan M. Z., Pavel N. I. (2011). "Dynamic scaling, data-collapseand Self-similarity in Barabasi-Albert networks". J. Phys. A: Math. Theor. 44 (17): 175101. arXiv:1101.4730. Bibcode:2011JPhA...44q5101K. doi:10.1088/1751-8113/44/17/175101.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Hassan M. K., Hassan M. Z. (2009). "Emergence of fractal behavior in condensation-driven aggregation". Phys. Rev. E. 79 (2): 021406. arXiv:0901.2761. Bibcode:2009PhRvE..79b1406H. doi:10.1103/physreve.79.021406. PMID 19391746.
- ↑ Dayeen F. R., Hassan M. K. (2016). "Multi-multifractality, dynamic scaling and neighbourhood statistics in weighted planar stochastic lattice". Chaos, Solitons & Fractals. 91: 228. arXiv:1409.7928. Bibcode:2016CSF....91..228D. doi:10.1016/j.chaos.2016.06.006.
- ↑ Peitgen, Heinz-Otto; Jürgens, Hartmut; Saupe, Dietmar; Maletsky, Evan; Perciante, Terry; and Yunker, Lee (1991). Fractals for the Classroom: Strategic Activities Volume One, p.21. Springer-Verlag, New York.
- ↑ Peitgen, et al (1991), p.2-3.
- ↑ Peitgen, et al (1991), p.2-3.
- ↑ Campbell, Lo and MacKinlay (1991) "Econometrics of Financial Markets ", Princeton University Press!
- ↑ Foote, Jonathan (30 October 1999). Visualizing music and audio using self-similarity. pp. 77–80. doi:10.1145/319463.319472. ISBN 978-1581131512. http://musicweb.ucsd.edu/~sdubnov/CATbox/Reader/p77-foote.pdf.
- ↑ Pareyon, Gabriel (April 2011). On Musical Self-Similarity: Intersemiosis as Synecdoche and Analogy. International Semiotics Institute at Imatra; Semiotic Society of Finland. p. 240. ISBN 978-952-5431-32-2. Archived from the original on 8 February 2017. https://web.archive.org/web/20170208034152/https://tuhat.helsinki.fi/portal/files/15216101/Pareyon_Dissertation.pdf. Retrieved 30 July 2018. (Also see Google Books)
其他链接
- "Copperplate Chevrons" — a self-similar fractal zoom movie
- "Self-Similarity" — New articles about Self-Similarity. Waltz Algorithm
自仿射
- Mandelbrot, Benoit B. (1985). "Self-affinity and fractal dimension" (PDF). Physica Scripta. 32 (4): 257–260. Bibcode:1985PhyS...32..257M. doi:10.1088/0031-8949/32/4/001.
- Sapozhnikov, Victor; Foufoula-Georgiou, Efi (May 1996). "Self-Affinity in Braided Rivers" (PDF). Water Resources Research. 32 (5): 1429–1439. doi:10.1029/96wr00490. Archived (PDF) from the original on 30 July 2018. Retrieved 30 July 2018.
- Benoît B. Mandelbrot (2002). Gaussian Self-Affinity and Fractals: Globality, the Earth, 1/F Noise, and R/S. ISBN 978-0387989938.
编者推荐
书籍推荐
《分形对象:形、机遇和维数 Fractals:From,Chance,and Dimension》
本书考察和研究出现在自然界中的若干典型分形对象,为我们提供了一个关于分形的内容,意义及方法的扼要介绍。尽管自该书第一版(法文版)问世以来,分形的理论及其应用发展极为迅速,并出现了大量的有关著作,但此书仍不失为分形理论最好的入门书之一
《大自然的分形几何 The Fractal Geometry of Nature》
这本书介绍了自然界中各种各样的分形理论,从海岸线、雪花,到河流、星系等自然现象,去阐述分形这一概念。作为多个学科的交叉,分形几何对以往欧氏几何不屑一顾(或说无能为力)的“病态”曲线(如科赫雪花曲线等)的全新解释,是人类认识客观世界不断开拓的必然结果。这说明欧氏几何只是对客观世界的近似反映,而分形几何则深化了这种认识,因此分形几何学是描述各种复杂自然曲线的大自然的几何学。
《市场的(错误)行为:风险、破产与收益的分形观点 The Misbehavior of Markets: A Fractal View of Financial Turbulence》
《市场的(错误)行为》以分形视角观察金融市场的行为,推翻了作为当代金融分析基础的“随机游走”理论。通过分形模型,市场表现被重新阐释。本书是现代金融理论标准工具和模型的一次革命性重估,书中的观点颠覆了成千上万投资者的既有观念。
网站资源
分形艺术网
分形艺术网是一个展示分形艺术之美,学习交流分形艺术创作的平台,其中包含了很多分形艺术作品及分形资源推荐。
视频资源
TED分享视频:伯努·瓦曼德布洛特: 分形和粗糙的艺术 Benoit Mandelbrot: Fractals and the Art of Roughness
Benoit Mandelbrot的研究使世界对分形有了更深刻的理解,分形是研究粗糙的广泛而有力的工具,在自然界和人类的作品中都是如此。该视频概述了分形的研究,以及它们为许多领域带来的颠覆性见解。
寻找隐藏的维 Hunting the Hidden Dimension
什么是电影特效,股票市场,和心脏病的共同点?它们连接了一个革命性的新的数学分支,改变了我们看世界,开辟了广阔的新领域,以科学的分析和理解。数学家们开发不规则碎片形是从单纯的好奇心到接触几乎每一个分科的理解,包括我们宇宙的命运。
课程推荐
集智百科文章
本中文词条由栗子CUGB审校,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。