标度不变性
在物理学、数学和统计学中,标度不变性 Scale Invariance是物体或者物理定律的一种特征,如果长度、能量或者其他变量的标度与一个公因子相乘,而不发生改变,因此也就代表某种普遍性。
这种变换的专业名称是膨胀 Dilatation,膨胀也可以形成一个更大共形对称 Conformal Symmetry的一部分。
- 在数学中,标度不变性通常指单个函数或曲线的不变性。与此密切相关的概念是自相似性 Self-similarity,其中函数或曲线在膨胀的离散子集下是不变的。随机过程的概率分布也可能表现出这种标度不变性或自相似性。
- 在经典场论中,标度不变性最常用于整个理论在膨胀条件下的不变性。这些理论通常描述没有特征长度标度的经典物理过程。
- 在量子场论中,标度不变性可以用粒子物理学来解释。在标度不变的理论中,粒子相互作用的强度并不取决于所涉及粒子的能量。
- 在统计力学中,标度不变性是相变的一个特征。在相变或临界点附近,在所有长度标度上都出现了波动,因此,人们应该寻找一个明确的标度不变的理论来描述这一关键现象。这些理论是标度不变的统计场理论,在形式上与标度不变的量子场理论非常相似。
- 普适性 Universality是指差异巨大的微观系统在相变时可以表现出相同的行为。因此,许多不同系统中的相变可以用相同的基本标度不变理论来描述。
- 一般来说,无量纲量是标度不变量。统计学中的类似概念是标准化矩 Standardized Moments,它是变量的标度不变统计量,而非标准化矩不是。
标度不变曲线与自相似性
在数学中,我们会考虑函数或曲线在变量x重新标度下的标度性质。也就是说,人们对某些标度因子λ 对应下f (λx)的形状感兴趣,这些标度因子可以被视为长度或大小的重新标度。对于某些选择的指数Δ和所有的膨胀λ,要求f(x) 在所有重新标度下保持不变需要满足: [math]\displaystyle{ f(\lambda x)=\lambda^{\Delta}f(x) }[/math]。
这等价于f 是一个次数为Δ的齐次函数。
许多标变函数的实例是单项式:[math]\displaystyle{ f(x)=x^n }[/math],其中 Δ = n,且有:
- [math]\displaystyle{ f(\lambda x) = (\lambda x)^n = \lambda^n f(x)~ }[/math]。
一个标度不变曲线的例子是对数螺线(等角螺线) Logarithmic Spiral,这是一种在自然界中经常出现的曲线。在极坐标系中,螺旋线可以写成
- [math]\displaystyle{ \theta = \frac{1}{b} \ln(r/a)~。 }[/math]
在任意重新标度λ下,标度不变也允许曲线进行旋转;换句话说,θ(λr)与其旋转后的θ(r)一模一样。
射影几何
单项式标度不变性的概念在高维时推广到齐次多项式 Homogeneous Polynomial,更一般地推广到齐次函数 Homogeneous Function。齐次函数是射影空间的“土著”,齐次多项式在射影几何中作为射影簇 Projective Varieties进行研究。射影几何是数学中一个内容特别丰富的领域;在其最抽象的形式——概型Schemes的几何学中,它与弦理论 String Theory中的各种主题都有联系。
分形
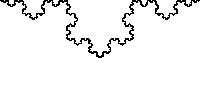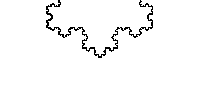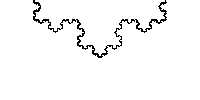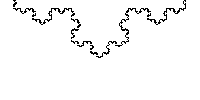
有时人们认为分形是标度不变的,尽管更准确地来说,应该说分形是自相似的。分形通常是在某个λ值的离散集合内等同于其本身,即使这样,有时也需要通过平移和旋转变换来实现。
因此,以∆ = 1的科赫雪花 Koch Curve缩放为例,但是该缩放只适用于λ = 1/3n,(n为整数)的值。此外,科赫雪花不仅在初始点,而且在某种意义上,在整条曲线上都可以找到其“缩影”。
某些分形可能同时具有多个标度因子,可以应用多重分形分析 Multi-Fractal Analysis进行研究。
周期性外部和内部射线是不变的曲线。
随机过程中的标度不变性
如果P(f )是频率f 处的平均期望幂,那么噪声依下式标度变化:
- [math]\displaystyle{ P(f) = \lambda^{-\Delta} P(\lambda f) }[/math]
当Δ= 0时对应白噪声 White noise,Δ=-1时对应粉红噪声 Pink noise,Δ=-2时对应布朗噪声 Brownian noise(更一般的是布朗运动 Brownian motion)。
更准确地说,随机系统中的标度变化涉及从所有可能的随机排列中选择一个特定排列的可能性。这一可能性可由概率分布给出。此外还需要更多的背景内容。概率和熵必然与一个特定排列的选定有关,但标度不变性与它们之间的相互联系还不明显。
标度不变分布的例子还有帕累托分布 Pareto distribution和齐夫分布 Zipfian distribution。
标度不变的Tweedie分布
Tweedie分布是指数弥散模型 Exponential Dispersion Models的一种特殊情况,是一类用于描述广义线性模型误差分布的统计模型,在可加卷积和再生卷积以及标度变换下具有闭包性[1]。这包括一些常见的分布:正态分布、泊松分布 Poisson distribution和伽玛分布 Gamma Distribution,以及其他一些非同寻常的分布,如复合泊松-伽玛分布、正稳定分布和极端稳定分布。由于它们固有的标度不变性,Tweedie随机变量 y 显示方差var(Y)与均值E(Y)之间服从幂律关系:
- [math]\displaystyle{ \text{var}\,(Y) = a[\text{E}\,(Y)]^p }[/math],
其中a和p是正常数。这种方差-均值的幂律关系在物理学文献中称为涨落标度 Fluctuation Scaling[2],在生态学文献中称为泰勒定律 Taylor's Law[3]。
随机序列由Tweedie分布控制,并通过展开箱的方法进行评估,在方差-均值幂律和幂律自相关之间表现出双条件关系。维纳-辛钦定理 Wiener–Khinchin Theorem进一步表明,在这些条件下,对于任何具有方差-均值幂律的序列,也会出现1/f噪声[4]。
收敛定理 Tweedie Convergence Theorem Tweedie为涨落标度和1/f噪声的广泛出现提供了一个假设性解释[5] 。本质上,它要求任何一个可以渐近地显示方差-均值幂律的指数弥散模型,需要在Tweedie模型的吸引域内表达一个方差函数。几乎所有具有有限累积母函数的分布函数都符合指数弥散模型,而大多数指数弥散模型都表现出这种形式的方差函数。因此,许多概率分布都有表达这种渐近行为的方差函数,而Tweedie分布成为了不同数据类型收敛的焦点[4]。
正如中心极限定理要求某些类型的随机变量以高斯分布为收敛焦点并表示白噪声一样,Tweedie收敛定理要求某些非高斯随机变量来表达1/f噪声和涨落标度[4]。
宇宙学
在宇宙物理学 Physical Cosmology,宇宙微波背景 Cosmic Microwave Background的空间分布功率频谱近似于标度不变函数。尽管在数学上这意味着该频谱服从幂律,但在宇宙学中“标度不变”一词表明,原始涨落 Primordial Fluctuations的振幅P(k),作为波数k的函数,是近似常数,也就是一个平谱。这种模式与宇宙膨胀论 Cosmic Inflation的主张是一致的。
经典场论中的标度不变性
经典场论一般用依赖于坐标x 的场或场集 φ 来描述。然后通过求解 φ 的微分方程来确定有效的场构型,这些方程被称为场方程。
对于一个具有标度不变性的理论,它的场方程应该在坐标的缩放下保持不变,并结合特定的场的缩放:
- [math]\displaystyle{ x\rightarrow\lambda x~ }[/math],
- [math]\displaystyle{ \varphi\rightarrow\lambda^{-\Delta}\varphi~ }[/math]。
参数 Δ 称为场的标度维数 Scaling Dimension,其大小取决于所考虑的理论。如果理论中没有固定长度的标度,标度不变性通常会成立。相反,如果存在固定的长度标度,则表明理论不具有标度不变性。
标度不变性的一个结果是:给定一个标度不变性场方程的解,我们可以通过适当地缩放坐标和场自动地找到其他解。具体来说,给定一个解φ(x),总有其他形式的解
- [math]\displaystyle{ \lambda^{\Delta}\varphi(\lambda x) }[/math]。
场结构中的标度不变性
对于特定的场构型φ(x),要具有标度不变性,我们就要满足:
- [math]\displaystyle{ \varphi(x)=\lambda^{-\Delta}\varphi(\lambda x) }[/math]。其中 Δ 是场的标度维数。
我们注意到这个条件限制性很强。一般来说,即使是标度不变场方程的解也不是标度不变的,在这种情况下,对称性出现自发破缺 Spontaneously Broken。
经典电磁学
标度不变的经典场论的一个实例是没有电荷和电流的电磁学。场是电场和磁场,E(x,t) 和 B(x,t),而它们的场方程是麦克斯韦方程组。
在没有电荷或电流的情况下,这些场方程采用波动方程的形式:
- [math]\displaystyle{ \nabla^2 \mathbf{E} = \frac{1}{c^2} \frac{\partial^2 \mathbf{E}}{\partial t^2} }[/math]
- [math]\displaystyle{ \nabla^2\mathbf{B} = \frac{1}{c^2} \frac{\partial^2 \mathbf{B}}{\partial t^2} }[/math]
其中 c 是光速。
这些场方程在进行如下变换下是不变的:
- [math]\displaystyle{ x\rightarrow\lambda x }[/math],
- [math]\displaystyle{ t\rightarrow\lambda t }[/math]。
此外,已知E(x, t)和B(x, t)是麦克斯韦方程组的解,则可以认为E(λx, λt)和B(λx, λt)也是解。
无质量标量场理论
标度不变经典场论的另一个例子是无质量标量场(注意名称“标量”与标度不变性无关)。标量场φ(x, t)是一组空间变量 x 和一个时间变量 t 的函数。
首先考虑线性理论。像上述的电磁场方程一样,这个理论的运动方程也是一个波动方程:
- [math]\displaystyle{ \frac{1}{c^2} \frac{\partial^2 \varphi}{\partial t^2}-\nabla^2 \varphi = 0 }[/math],
并且在进行如下变换时是不变的:
- [math]\displaystyle{ x\rightarrow\lambda x, }[/math]
- [math]\displaystyle{ t\rightarrow\lambda t }[/math]。
无质量是指在场方程中没有[math]\displaystyle{ \propto m^2\varphi }[/math]项。这一项通常称为“质量”项,它会破坏上述变换下的不变性。在相对论场理论 Relativistic Field Theories中,质量标度m在物理上等同于一个固定的长度标度:
- [math]\displaystyle{ L=\frac{\hbar}{mc} }[/math],
因此质量标量场理论不具有标度不变性也就不足为奇了。
φ4 理论
上面例子中的场方程在场中都是线性的,这意味着标度维数Δ并不是那么重要。然而,通常要求标量场的作用是无量纲的,这就固定了φ的标度维数。特别是:
- [math]\displaystyle{ \Delta=\frac{D-2}{2}, }[/math]
其中D是空间维数和时间维数的总和。
已知φ的标度维数,则无质量标量场理论的某些非线性修正也是标度不变的。例如,D=4的无质量φ4理论 φ4theory 。场方程是:
- [math]\displaystyle{ \frac{1}{c^2} \frac{\partial^2 \varphi}{\partial t^2}-\nabla^2 \varphi+g\varphi^3=0 }[/math]。
(注意,φ4的名称来自拉格朗日量的形式,它包含φ的四次幂)
当D=4(如三维空间维数和一维时间维数)时,标量场标度维数为Δ=1。场方程在进行如下变换下是不变的:
- [math]\displaystyle{ x\rightarrow\lambda x, }[/math]
- [math]\displaystyle{ t\rightarrow\lambda t, }[/math]
- [math]\displaystyle{ \varphi (x)\rightarrow\lambda^{-1}\varphi(x) }[/math]。
关键是参数g必须是无量纲的,否则就会引入一个固定的长度标度到理论中:对于φ4理论,只有在D=4时才会出现这种情况。注意,在这些变换下,函数φ的参数是不变的。
量子场论中的标度不变性
量子场论(QFT)的标度依赖性的特征是其耦合参数依赖于给定物理过程的能量标度。这种能量依赖由重正化群描述,并编码在理论的β函数 Beta-function中。
对于具有标度不变性的量子场论(QFT),其耦合参数必须与能量标度无关,这由理论中β函数的消失来表示。这类理论也被称为相应重整化群流的固定点[6]。
量子电动力学
标度不变量子场论的一个简单实例是没有带电粒子的量子化电磁场。这个理论实际上没有耦合参数(因为光子是无质量和非相互作用的) ,因此是标度不变的,这很像经典理论。
然而在自然界中,电磁场是与带电粒子耦合的,比如电子。描述光子和带电粒子相互作用的量子场论是量子电动力学(QED),而这个理论并不是标度不变的。我们可以从量子电动力学的β函数中得到这一认识。这就告诉我们电荷(在理论上是耦合参数)随着能量的增加而增加。因此,尽管没有带电粒子的量子化电磁场是标度不变的,量子电动力学却不是标度不变的。
无质量标量场理论
自由的、无质量的量子化标量场理论 Quantized Scalar Field Theory没有耦合参数。因此,像经典的版本一样,它是标度不变的。在重整化群的范畴中,这个理论称做高斯定点 Gaussian Fixed Point。
然而,尽管经典的无质量φ4理论在D=4时是标度不变的,但量子化的版本却不是如此。我们可以从耦合参数g的β函数中看出这一点。
虽然量子化无质量φ4不是标度不变的,但除了高斯定点外,确实存在标度不变的量子化标量场理论。例如:威尔逊-费雪定点 Wilson-Fisher Fixed Point。
共形场论
在完全共形对称条件下,标度不变的量子场论几乎总是不变的,对此类量子场论的研究就是共形场论(CFT)。共形场论中的算子具有定义明确的标度维数,类似于前面所讨论的经典场标度维数 ∆。然而,共形场论中算子的标度维数与经典理论中场的标度维数不同。在共形场论中出现的附加贡献称做异常标度维数 Anomalous Scaling Dimensions。
标度与共形异常
上面的φ4理论例子表明,量子场论的耦合参数可以是标度依赖的,即使相应的经典场论是标度不变(或共形不变)。如果是这种情况,则称经典标度(或共形)不变性为异常。经典的标度不变场论,当量子效应打破其中的标度不变性,可以为接近指数级膨胀的早期宇宙提供了一种解释,即为宇宙膨胀 Cosmic Inflation,只要该理论可以通过微扰理论 Perturbation Theory研究[7]。
相变
在统计力学中,当某个系统经历相变时,其波动可以用标度不变的统计场论来描述。对于在D空间维度中处于平衡状态(即时间无关)的系统,相应的统计场论形式上类似于D维共形场论。这类问题中的标度维数通常称为临界指数 Critical Exponents,原则上可以在适当的共形场论中计算这些指数。
伊辛模型
将本文中的许多观点联系在一起的一个实例是伊辛模型的相变,这是一个关于铁磁物质的简单模型。还是一个具有共形场论描述的统计力学模型。该系统由一系列格子点位组成,这些点位构成了一个D维的周期格子。与每个格子位置相关联的是磁矩或自旋,这个自旋可以取 +1或-1。(这些状态也分别称为向上和向下。)
关键地是,伊辛模型具有自旋-自旋相互作用,这使得两个相邻的自旋在能量上更有利于排列。另一方面,热波动通常会给自旋的排列带来随机性。在某些临界温度(Tc)下,就会发生自发磁化 Spontaneous Magnetization。这意味着在临界温度以下,自旋-自旋相互作用将开始占据主导地位,并且在两个方向中的任一方向上存在部分自旋的净排列。
在这个临界温度下,人们想要计算的物理量之一是存在距离的自旋之间的相互关系。此处通式为:
[math]\displaystyle{ G(r)\propto\frac{1}{r^{D-2+\eta}} }[/math],
对于某个特定的[math]\displaystyle{ \eta }[/math]值,这是一个临界指数的例子。
共形场论描述
在临界温度处的波动是标度不变的,因此相变时的伊辛模型可以用标度不变的统计场论来描述。事实上,这个理论就是威尔逊-费雪定点,一个特殊的标度不变标量场理论。
此处,G(r)理解为标量场的相关函数
- [math]\displaystyle{ \langle\phi(0)\phi(r)\rangle\propto\frac{1}{r^{D-2+\eta}} }[/math]。
现在我们可以把已经看到的一些想法联系起来。
由上可知,这种相变的临界指数也是异常维数。这是因为标量场的经典维数:
- [math]\displaystyle{ \Delta=\frac{D-2}{2} }[/math]
修正为:
- [math]\displaystyle{ \Delta=\frac{D-2+\eta}{2}, }[/math]
其中D 是伊辛模型格子的维数。
因此,共形场论中的这个异常维数与伊辛模型相变的特定临界指数是相同的。
对于维度D ≡ 4−ε,可以使用epsilon展开式近似地计算η,并且可以发现:
- [math]\displaystyle{ \eta=\frac{\epsilon^2}{54}+O(\epsilon^3) }[/math]。
在物理上很有趣的三维空间情况下,我们有ε=1,因此这种膨胀并不严格可靠。然而,半定量的预测是η在三维上的数值很小。
另一方面,在二维情况下,伊辛模型是完全可解的。特别地,它等价于最小模型 Minimal Model之一,即一组很好理解的共形场论,并且可以精确地计算η(和其他临界指数):
- [math]\displaystyle{ \eta_{_{D=2}}=\frac{1}{4} }[/math]。
施拉姆—洛纳演化
某些二维共形场论的异常维数可能与随机游动的典型分形维数有关,其中随机游动是通过施拉姆-洛纳演化(SLE)定义的。正如我们上面所看到的,共形场论描述了相变的物理过程,因此我们可以把某些相变的临界指数与这些分形维数联系起来。例如,二维临界伊辛模型和更一般的二维临界波茨模型。将其他二维共形场论与施拉姆-洛纳演化联系起来是一个活跃的研究领域。
普适性
普适性的现象存在于许多不同的物理系统中。它表达了不同的微观物理过程可以在相变中产生相同的标度行为的观点。普适性的典型例子涉及以下两个系统:
- 伊辛模型相变,如上所述。
- 经典流体中的液-气转变。
尽管这两个系统的微观物理过程完全不同,但它们的临界指数却是相同的。此外,我们可以使用相同的统计场论计算这些指数。在相变或临界点,值得我们注意的是,在所有长度标度上都会出现波动,因此我们应该寻找一个标度不变的统计场论来描述这种现象。从某种意义上说,普适性就是指观察到这样的标度不变理论相对稀少。
由同一标度不变理论描述的不同微观理论的集合被称为普适性类。属于普适性类别的其他系统有:
- 沙堆中的塌落现象。发生塌落的可能性与塌落的规模服从幂律,而且可以看到塌落发生在所有不同的尺度上。
- 互联网网络中断的频率,是其规模和持续时间的函数。
- 期刊论文引用的频率(在所有论文的所有引用网络中考虑),是任一篇给定论文引用次数的函数。
- 从钢铁、岩石再到纸张等材料的裂缝和撕裂的形成和扩展。撕裂方向的变化,或破裂表面的粗糙度,与尺度成幂律关系。
- 电介质的电击穿现象,类似于裂缝和撕裂。
- 流体通过无序介质的渗透,如石油通过破碎的岩层,或水通过滤纸,如色谱法。幂律标度变化将流速与裂缝的分布联系起来。
- 分子在溶液中的扩散和扩散限制聚集 Diffusion-limited Aggregation现象。
- 在受重力作用而震动混杂的混合物中,不同大小的岩石碎块的分布。
最关键的是,对于所有这些不同的系统来说,它们的行为都类似于相变,并且可以用统计力学的方式和标度不变的统计场论来描述。
标度不变性的其他实例
无应力牛顿流体力学
在一定条件下,流体力学是一种标度不变的经典场论。流场包括流体流动速度[math]\displaystyle{ \mathbf{u}(\mathbf{x},t) }[/math]、流体密度[math]\displaystyle{ \rho(\mathbf{x},t) }[/math]和流体压力[math]\displaystyle{ P(\mathbf{x},t) }[/math]。这些场必须同时满足纳维-斯托克斯方程 Navier–Stokes equation和连续性方程 Continuity Equation。对于牛顿流体 Newtonian Fluid,它们有各自的形式:
- [math]\displaystyle{ \rho\frac{\partial \mathbf{u}}{\partial t}+\rho\mathbf{u}\cdot\nabla \mathbf{u} = -\nabla P+\mu \left(\nabla^2 \mathbf{u}+\frac{1}{3}\nabla\left(\nabla\cdot\mathbf{u}\right)\right) }[/math]
- [math]\displaystyle{ \frac{\partial \rho}{\partial t}+\nabla\cdot \left(\rho\mathbf{u}\right)=0 }[/math]
其中[math]\displaystyle{ \mu }[/math]是动态黏度 Dynamic Viscosity。
为了推导这些方程的尺度不变性,我们指定一个状态方程,将流体压力与流体密度联系起来。状态方程取决于流体的类型及其所处的条件。例如,我们考虑等温理想气体,它满足:
- [math]\displaystyle{ P=c_s^2\rho, }[/math],
其中[math]\displaystyle{ c_s }[/math]是流体中声速。给定这个状态方程,纳维-斯托克斯方程和连续性方程在进行如下变换时是不变的:
- [math]\displaystyle{ x\rightarrow\lambda x, }[/math]
- [math]\displaystyle{ t\rightarrow\lambda^2 t, }[/math]
- [math]\displaystyle{ \rho\rightarrow\lambda^{-1} \rho, }[/math]
- [math]\displaystyle{ \mathbf{u}\rightarrow\mathbf{u}。 }[/math]
- 已知解[math]\displaystyle{ \mathbf{u}(\mathbf{x},t) }[/math]和[math]\displaystyle{ \rho(\mathbf{x},t) }[/math],我们自然可以得到[math]\displaystyle{ \lambda\mathbf{u}(\lambda\mathbf{x},\lambda^2 t) }[/math]和[math]\displaystyle{ \lambda\rho(\lambda\mathbf{x},\lambda^2 t) }[/math]也是解。
计算机视觉
在计算机视觉和生物视觉中,由于图像的透视映射和世界上物体的物理尺寸不同而产生了标度变换。在这些领域中,标度不变性是指当图像域的局部尺度发生变化时,图像数据的图像描述或视觉表达效果保持不变[8] 。在归一化导数响应的尺度上检测局部极大值为从图像数据中获取标度不变性提供了一个通用框架[9][10]。应用的例子包括斑点检测 Blob Detection、角点检测 Corner Detection、脊线检测 Ridge Detection和通过标度不变特征变换 Scale-Invariant Feature Transform进行的目标识别。
参见
- 逆平方势
- 幂律
- 无尺度网络定律
参考文献
- ↑ Jørgensen, B. (1997). The Theory of Dispersion Models. London: Chapman & Hall. ISBN 978-0412997112.
- ↑ Eisler, Z.; Bartos, I.; Kertész, J. (2008). "Fluctuation scaling in complex systems: Taylor's law and beyond". Adv Phys. 57 (1): 89–142. arXiv:0708.2053. Bibcode:2008AdPhy..57...89E. doi:10.1080/00018730801893043. S2CID 119608542.
- ↑ Kendal, W. S.; Jørgensen, B. (2011). "Taylor's power law and fluctuation scaling explained by a central-limit-like convergence". Phys. Rev. E. 83 (6): 066115. Bibcode:2011PhRvE..83f6115K. doi:10.1103/PhysRevE.83.066115. PMID 21797449.
- ↑ 4.0 4.1 4.2 Kendal, W. S.; Jørgensen, B. (2011). "Tweedie convergence: A mathematical basis for Taylor's power law, 1/f noise, and multifractality" (PDF). Phys. Rev. E. 84 (6): 066120. Bibcode:2011PhRvE..84f6120K. doi:10.1103/PhysRevE.84.066120. PMID 22304168.
- ↑ Jørgensen, B.; Martinez, J. R.; Tsao, M. (1994). "Asymptotic behaviour of the variance function". Scand J Statist. 21 (3): 223–243. JSTOR 4616314.
- ↑ J. Zinn-Justin (2010) Scholarpedia article "Critical Phenomena: field theoretical approach".
- ↑ Salvio, Strumia (2014-03-17). "Agravity". JHEP. 2014 (6): 080. arXiv:1403.4226. Bibcode:2014JHEP...06..080S. doi:10.1007/JHEP06(2014)080.
- ↑ Lindeberg, T. (2013) Invariance of visual operations at the level of receptive fields, PLoS ONE 8(7):e66990.
- ↑ Lindeberg, Tony (1998). "Feature detection with automatic scale selection". International Journal of Computer Vision. 30 (2): 79–116. doi:10.1023/A:1008045108935. S2CID 723210.
- ↑ T. Lindeberg (2014) "Scale selection", Computer Vision: A Reference Guide, (K. Ikeuchi, Editor), Springer, pages 701-713.
拓展阅读
- Zinn-Justin, Jean (2002). Quantum Field Theory and Critical Phenomena. Oxford University Press. Extensive discussion of scale invariance in quantum and statistical field theories, applications to critical phenomena and the epsilon expansion and related topics.
- DiFrancesco, P.; Mathieu, P.; Senechal, D. (1997). Conformal Field Theory. Springer-Verlag.
- Mussardo, G. (2010). Statistical Field Theory. An Introduction to Exactly Solved Models of Statistical Physics. Oxford University Press.
编者推荐
伊辛模型 Ising Model - 集智百科 (swarma.org)
伊辛模型最初是用于解释铁磁系统相变的一个简单模型,在通过数轮开发后,人们逐渐认识到了它作为相变模型的普适性:无论是铁原子还是水分子组成的系统,在临近相变时,它们都具有相同的临界指数。到今天,伊辛模型已经被应用于科学领域的方方面面,但精确求解三维伊辛模型的问题仍然困扰着物理学家,这呼唤着科学方法的新变革。
几十年来,数学家一直希望证明在在物理系统从一种状态转变为另一种状态时,对称性是普遍存在的。被称为共形不变性(conformal invariance)的对称性,实际上包含三个独立的对称性:旋转对称性、平移对称性和标度不变性。近期,一些数学家证明,在临界时刻,被称为旋转不变性的对称性是许多物理系统的普遍属性。
“贫穷限制了我们的想像力”是最近非常流行的网络语言。在这儿采用这个副标题不是为了哗众取宠,而是因为这个讲座的内容真的和经济金融相关,而且介绍的内容真的会超出你的想象力。本文节选自陈清华的线上讲座《解读幂律与无标度网络——贫穷限制了我们的想象力》。
本中文词条由栗子CUGB参与编译和审校,糖糖编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。