“WS小世界模型”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第5行： 第5行：
 
'''WS小世界模型 Watts–Strogatz model '''是一种[[随机图]]生成模型，其生成的图具有[[小世界属性]]，包括较短的平均节点间距离 average path length和高集聚系数clustering coefficient。该模型由[[邓肯·瓦茨 Duncan J. Watts]]和[[史蒂夫·斯托加茨 Steven Strogatz]]在1998年两人联合发表于《Nature》的论文中提出
 
'''WS小世界模型 Watts–Strogatz model '''是一种[[随机图]]生成模型，其生成的图具有[[小世界属性]]，包括较短的平均节点间距离 average path length和高集聚系数clustering coefficient。该模型由[[邓肯·瓦茨 Duncan J. Watts]]和[[史蒂夫·斯托加茨 Steven Strogatz]]在1998年两人联合发表于《Nature》的论文中提出
 
<ref name=WS>{{Cite journal | last1 = Watts | first1 = D. J. | authorlink1 =  | last2 = Strogatz | first2 = S. H. | authorlink2 =  | title = Collective dynamics of 'small-world' networks | journal = Nature | volume = 393 | issue = 6684 | pages = 440–442 | doi = 10.1038/30918 | year = 1998 | url = http://worrydream.com/refs/Watts-CollectiveDynamicsOfSmallWorldNetworks.pdf | pmid = 9623998 | pmc =  | bibcode = 1998Natur.393..440W }}</ref>
 
<ref name=WS>{{Cite journal | last1 = Watts | first1 = D. J. | authorlink1 =  | last2 = Strogatz | first2 = S. H. | authorlink2 =  | title = Collective dynamics of 'small-world' networks | journal = Nature | volume = 393 | issue = 6684 | pages = 440–442 | doi = 10.1038/30918 | year = 1998 | url = http://worrydream.com/refs/Watts-CollectiveDynamicsOfSmallWorldNetworks.pdf | pmid = 9623998 | pmc =  | bibcode = 1998Natur.393..440W }}</ref>
−
。Watts在其广受欢迎的科学读物[https://en.wikipedia.org/wiki/Six_Degrees:_The_Science_of_a_Connected_Age 《Six Degrees》]中使用</math>\beta</math>来阐述该模型，这之后，该模型也被称为（沃茨）</math>\beta</math> 模型。
+
。Watts在其广受欢迎的科学读物[https://en.wikipedia.org/wiki/Six_Degrees:_The_Science_of_a_Connected_Age 《Six Degrees》]中使用</math>\beta</math>来阐述该模型，这之后，该模型也被称为（沃茨）<\math>\beta<\math> 模型。
  
  

2020年8月12日 (三) 20:54的版本

WS小世界模型 Watts–Strogatz model 是一种随机图生成模型，其生成的图具有小世界属性，包括较短的平均节点间距离 average path length和高集聚系数clustering coefficient。该模型由邓肯·瓦茨 Duncan J. Watts和史蒂夫·斯托加茨 Steven Strogatz在1998年两人联合发表于《Nature》的论文中提出 [1] 。Watts在其广受欢迎的科学读物《Six Degrees》中使用</math>\beta</math>来阐述该模型，这之后，该模型也被称为（沃茨）<\math>\beta<\math> 模型。


模型基本原理

对随机图的正式研究可追溯至 保尔·厄多斯 Paul Erdős和阿尔弗烈德·瑞利 Alfréd Rényi的工作 [2] 。他们所考虑的图，也就是现在所谓的经典图或ER随机图模型，给许多应用提供了简单而强有力的模型。


但ER图并不具有我们观察到的许多实际网络所拥有的两个重要属性：

  1. 不能生成局部集聚 local clustering 和三元闭合 triadic closures(网络有三元闭合、三元闭包等释义）。相反，因为图中两个节点有恒定、随机且独立的概率彼此相连，ER随机图模型的集聚系数较低。
  2. 不能解释中心节点 hub 的构成。在形式上，ER随机图模型的度分布收敛于泊松分布 Poisson distribution ，而不是我们在现实世界中观测到的、无标度网络 scale-free networks 的幂律分布 power law[3]


WS小世界模型是针对于第一条局限性来设计的最简可能模型。它在解释了集聚的同时保持了ER模型较短的平均节点间距离，这是通过在近似ER图的随机化结构和正则环点阵 regular ring lattice中进行内插得到的。因而，该模型至少能够部分解释许多网络中的“小世界”现象 "small-world" phenomena，比如电网、秀丽隐杆线虫 C. elegans的神经网络、电影演员的社交网络、以及芽殖酵母脂肪代谢的信息交流 [4] 。

算法

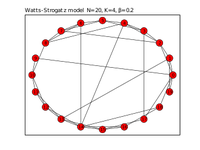
假设所期望的节点数为[math]\displaystyle{ N }[/math]，平均度为[math]\displaystyle{ K }[/math]（假定[math]\displaystyle{ K }[/math]为偶数）和一个特殊的参数[math]\displaystyle{ \beta }[/math] ，满足[math]\displaystyle{ 0\leq \beta \leq 1 }[/math]，且[math]\displaystyle{ N\gg K\gg lnN\gg 1 }[/math]。


该模型以下述方式构建了一个具有[math]\displaystyle{ N }[/math]个节点，[math]\displaystyle{ \frac{NK}{2} }[/math]条边的无向图：

  1. 构建一个正则环点阵。该图有[math]\displaystyle{ N }[/math]个节点，每个节点和[math]\displaystyle{ K }[/math]个相邻的节点相连，其中每一侧有[math]\displaystyle{ K/2 }[/math]个。即是，若每个节点用[math]\displaystyle{ n_{0},...,n_{N-1} }[/math]标示，当且仅当[math]\displaystyle{ 0\lt \left | i-j \right |\mod(N-1-\frac{K}{2})\leq \frac{K}{2} }[/math]时，存在边[math]\displaystyle{ (n_{i},n_{j}) }[/math]。
  2. 对于每个节点[math]\displaystyle{ n_{i}=n_{0},...,n_{N-1} }[/math]，选出其与最右侧第[math]\displaystyle{ K/2 }[/math]相邻节点之间的边，即满足[math]\displaystyle{ n_{i} \lt n_{j} \leq n_{i} + K/2 }[/math]的所有边 [math]\displaystyle{ (n_{i},n_{j}\mod N) }[/math] ，以概率[math]\displaystyle{ \beta }[/math]将其重新连接。重新连接的过程是把边 [math]\displaystyle{ (n_{i},n_{j}\mod N) }[/math] 替换为边 [math]\displaystyle{ (n_{i},n_{k}) }[/math] ，其中[math]\displaystyle{ k }[/math]以一致的随机性从所有可能的节点选出，并且避免出现自回路[math]\displaystyle{ (k\neq i) }[/math]和重复连接（边 [math]\displaystyle{ (n_{i},n_{{k}'}) }[/math] ，其中[math]\displaystyle{ {k}'=k }[/math]，在该算法中不会出现）的情况。

特性

该模型基础的点阵图结构产生了局部集聚的网络，而随机的重新连接则大大减少了平均节点间距离。其算法引入了大约[math]\displaystyle{ \beta \tfrac{NK}{2} }[/math]条非点阵边。改变[math]\displaystyle{ \beta }[/math]的值可以在正则环点阵（[math]\displaystyle{ \beta =0 }[/math]）和接近ER随机图的结构[math]\displaystyle{ (\beta = }[/math][math]\displaystyle{ 1 }[/math]，[math]\displaystyle{ G }[/math][math]\displaystyle{ (N,p) }[/math]满足[math]\displaystyle{ p=\frac {K}{N-1}) }[/math]间进行内插。由于每一个节点都与至少[math]\displaystyle{ K/2 }[/math]个其他节点相连，该模型并没符合真实的ER模型。


我们感兴趣的三个特性是平均节点间距离、集聚系数和度分布。

Watts–Strogatz 小世界模型，由igraph生成，Cytoscape 2.5进行可视化，100个节点
Watts_strogatz图

平均节点间距离

  • 对于环形点阵，平均节点间距离是[math]\displaystyle{ \ell(0)=N/2K\gg 1 }[/math]，且随系统规模线性变化；
  • 对于极限情况[math]\displaystyle{ (\beta \rightarrow 1) }[/math]，该图趋近于随机图，平均节点间距离[math]\displaystyle{ \ell(1)=\frac{lnN}{lnK} }[/math]，但实际上不收敛于此；
  • 在区间[math]\displaystyle{ (0\lt \beta \lt 1) }[/math]内，平均节点间距离随着[math]\displaystyle{ \beta }[/math]的增大迅速下降，并很快接近于其极限值。


集聚系数

  • 对于环形点阵，集聚系数[5] 为[math]\displaystyle{ C(0)=\frac{3(K-2)}{4(K-1)} }[/math]，因此随着K的增大趋向于[math]\displaystyle{ 3/4 }[/math]，且与系统规模无关；
  • 对于[math]\displaystyle{ \beta \rightarrow 1 }[/math]的极限情况，集聚系数与经典随机图同阶，[math]\displaystyle{ C=\frac{K}{N-1} }[/math]，与系统规模成反比；区间内的集聚系数则十分接近于正则环点阵的系数值，只有在[math]\displaystyle{ \beta }[/math]相对较大时才会下降，这就导致了在一定区间范围内平均节点间距离下降迅速，而集聚系数保持相对恒定的情形，也就解释了“小世界”现象。
  • 如果我们用巴拉特 Barrat和魏格特 Weigt的方法[6]，即是用一个节点的相邻节点之间的平均边数和这些相邻节点之间可能的平均边数之商来定义集聚系数[math]\displaystyle{ C'(\beta) }[/math]，或者说:
[math]\displaystyle{ C'(\beta)=\frac{3\times \text{number of triangles}}{\text{number of connected triples}} }[/math]
可得出[math]\displaystyle{ C'(\beta)\sim C(0)(1-\beta)^{3} }[/math]


度分布

[math]\displaystyle{ P(k) = \sum_{n=0}^{f(k,K)} {{K/2}\choose{n}} (1-\beta)^n \beta^{K/2-n} \frac{(\beta K/2)^{k-K/2-n}}{(k-K/2-n)!} e^{-\beta K/2} }[/math]
[math]\displaystyle{ k_{i} }[/math]是第[math]\displaystyle{ i }[/math]个节点的边数或称为度。这里[math]\displaystyle{ k\geq K/2 }[/math]，[math]\displaystyle{ f(k,K)=min(k-K/2,K/2) }[/math]。
  • 度分布的形状类似于随机图，在[math]\displaystyle{ k }[/math][math]\displaystyle{ = }[/math][math]\displaystyle{ K }[/math]处取得明显峰值，对于较大的[math]\displaystyle{ \left | k-K\right | }[/math]呈指数衰减。
  • 网络的拓扑相对而言是齐次的，也即所有的节点都有相同的度。

例子

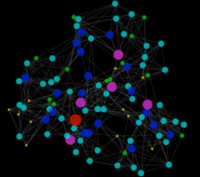
小世界网络例子

在现实世界的很多现象中，都能够看到小世界属性，这包括网络中的导航菜单、食物网、电网、代谢处理网络(metabolite processing networks)、脑神经网络、选民网络、电话呼叫图、社交影响网络等等。文化网络[7]与单词共现网络[8]也被证明是小世界网络。

相连的蛋白质网络同样具有小世界性质，例如遵从幂律的度分布。[9]类似地还有转录网络，其节点为基因，如果某一个基因对另一个基因有上调或下调的遗传影响，且这些基因彼此相连，这一网络就具有小世界网络的性质。[10]

非小世界网络例子

另一个例子就是人与人之间的“六度分离”理论，这里默认的适用领域是一群在任意时刻都活着的人。阿尔伯特·爱因斯坦与亚历山大大帝之间的分离度，几乎肯定是大于30的[11]，而且这个世界并不具备小世界属性。一个同样不具备小世界性质的网络还有“曾去同一家学校上学”的网络：如果两个人加入某一所大学的时间差了10年，他们不太可能在学生团体中有共同的熟人。

类似的，消息传播过程中必须要通过的中继站点的数量并不总是很小的。回溯到邮件还需要手工投递或骑马寄送的时期，一封信件从它的起点到终点所需要转手的次数，会比现在大上很多。可视电报（约存在于1800-1850年）时代，消息易手的次数，要由两个站点之间是否是在视线连接范围内决定。

如果没有检验隐含假设，可能会对图“望图生义”，偏向于寻找小世界网络（一个例子就是发表性偏倚导致的文件抽屉问题（file drawer））。

局限性

该模型的主要局限性是会产生不符实际的度分布。相较而言，现实中的网络通常是非齐次的无标度网络，有中心节点的存在和无标度的度分布。考虑到此，这样的网络可以用偏好依附模型 preferential attachment model来更好的描述，比如BA网络模型。（另一方面，BA模型没有产生真实网络中出现的高集聚特性，而这个弱点是WS小世界模型所不具备的。因此，WS小世界模型和BA模型均不应被看成是完全符合实际的。）WS小世界模型也暗含了固定的节点数，所以也不能用来描述网络的生长。

应用

社会学应用

小世界网络对社会运动群体的优势在于，它们由于采用了高度互联的节点的过滤设备，因而对变化具有一定的抗性，以及它有效地实现了，在中继信息的同时，保持了连接网络所需的最少链路数”。[12]

William Finnegan在社会学论证提出，小世界网络可直接适用于亲和团体（Affinity Group）理论。亲和团体指的是旨在实现某个较大目标或功能的小型半独立社会运动团体。虽然在节点级别上并没有严格的隶属架构，但作为连接节点的少数高连接性成员，能够通过网络连接组织内的不同群体。这种小世界网络已被证明是一种极其有效的抗议警察行动的组织策略。[13]Clay Shirky认为，通过小世界网络创造的社交网络越大，高连接性结点在网络内的价值就越高。[12]同理可适用于亲和团体模型，即每个团体内只有少数人与外部团体相联系，从而极大提高了灵活性和适应性。这方面的一个实践案例是William Finnegan在概括1999年西雅图世贸组织抗议活动时，所提到的亲和团体中的小世界网络。

地球科学应用

许多研究地质学和地球物理学的网络，已被证明具有小世界网络的特征。在裂缝系统和多空物质中被定义的网络，已经显示出了这些特征。[14]南加州地区的地震网络或许就是一个小世界网络。[15]上述提及的例子所发生的空间尺度大相径庭，也证明了在地球科学中，这一现象不受空间尺度大小所影响，具备尺度不变性（scale invariance）。气候网络或许也可被视作小世界网络，其中的联系具备长度不一的尺度。[16]

计算应用

小世界网络已被用于估算存储于大型数据库中信息的可用性。这种度量方法被称为“小世界数据变换法”[17][18]数据库链接与小世界网络对齐度越高，用户越有可能在将来提取到信息。这种可用性通常以牺牲存储在同等空间中的信息量为代价来取得。

Freenet和比特币点对点网络已经被证明在模拟中构筑了小世界网络[19]，使得信息的存储和提取，能够随着网络扩展，而有效扩张。

大脑中的小世界网络

大脑中连接[20]与皮层神经元的同步网络[21]都体现出了小世界拓扑结构。

小世界神经元网络可以呈现出短期记忆。Solla等人提出的计算机模型具有两个稳定状态[22][23]——一种被认为在记忆存储中十分重要的特性（被称为双稳态）。激活脉冲在神经元之间产生自我维持的通信活动循环。第二波脉冲则终止这一活动。脉冲让这一系统在稳定状态间切换：流动（记录“记忆”）以及停滞（保留记忆）。小世界神经元网络也被用于建模，了解病情发作的原理。[24]

在更一般的层次上，大脑中的许多大规模神经网络，例如视觉系统和脑干，都体现出了小世界特性。[25]

参见


参考文献

  1. ↑ Watts, D. J.; Strogatz, S. H. (1998). "Collective dynamics of 'small-world' networks" (PDF). Nature. 393 (6684): 440–442. Bibcode:1998Natur.393..440W. doi:10.1038/30918. PMID 9623998.
  2. ↑ Erdos, P. (1960). "Publications Mathematicae 6, 290 (1959); P. Erdos, A. Renyi". Publ. Math. Inst. Hung. Acad. Sci. 5: 17.
  3. ↑ Ravasz, E. (30 August 2002). "Hierarchical Organization of Modularity in Metabolic Networks". Science. 297 (5586): 1551–1555. arXiv:cond-mat/0209244. Bibcode:2002Sci...297.1551R. doi:10.1126/science.1073374. PMID 12202830.
  4. ↑ Al-Anzi, Bader; Arpp, Patrick; Gerges, Sherif; Ormerod, Christopher; Olsman, Noah; Zinn, Kai (2015). "Experimental and Computational Analysis of a Large Protein Network That Controls Fat Storage Reveals the Design Principles of a Signaling Network". PLOS Computational Biology. 11 (5): e1004264. Bibcode:2015PLSCB..11E4264A. doi:10.1371/journal.pcbi.1004264. PMC 4447291. PMID 26020510.
  5. ↑ Albert, R., Barabási, A.-L. (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  6. ↑ Barrat, A.; Weigt, M. (2000). "On the properties of small-world network models". European Physical Journal B. 13 (3): 547–560. arXiv:cond-mat/9903411. doi:10.1007/s100510050067.
  7. ↑ #" 'n Kwantifisering van kleinwêreldsheid in Afrikaanse kultuurnetwerke in vergelyking met ander komplekse netwerke | LitNet". LitNet. 2015-11-05. Retrieved 2017-02-27.
  8. ↑ #"Die statistiese eienskappe van geskrewe Afrikaans as 'n komplekse netwerk | LitNet". LitNet. 2017-02-09. Retrieved 2017-02-27.
  9. ↑ #Bork, P.; Jensen, LJ; von Mering, C.; Ramani, A.; Lee, I.; Marcotte, EM. (2004). "Protein interaction networks from yeast to human" (PDF). Current Opinion in Structural Biology. 14 (3): 292–299. doi:10.1016/j.sbi.2004.05.003. PMID 15193308.
  10. ↑ #Van Noort, V; Snel, B; Huynen, MA. (Mar 2004). "The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model". EMBO Rep. 5 (3): 280–4. doi:10.1038/sj.embor.7400090. PMC 1299002 Freely accessible. PMID 14968131.
  11. ↑ #Einstein and Alexander the Great lived 2202 years apart. Assuming an age difference of 70 years between any two connected people in the chain that connects the two, this would necessitate at least 32 connections between Einstein and Alexander the Great.
  12. ↑ 12.0 12.1 #Shirky, Clay. 2008. Here Comes Everybody
  13. ↑ #Finnegan, William "Affinity Groups and the Movement Against Corporate Globalization"
  14. ↑ #X. S. Yang, Small-world networks in geophysics, Geophys. Res. Lett., 28(13), 2549–2552 (2001)
  15. ↑ #A. Jimenez, K. F. Tiampo, and A. M. Posadas, Small-world in a seismic network: the California case, Nonlin. Processes Geophys., 15, 389–395 (2008)
  16. ↑ #Gozolchiani, A.; Havlin, S.; Yamasaki, K. (2011). "Emergence of El Niño as an Autonomous Component in the Climate Network". Physical Review Letters. 107 (14): 148501. arXiv:1010.2605 Freely accessible. Bibcode:2011PhRvL.107n8501G. doi:10.1103/PhysRevLett.107.148501. ISSN 0031-9007. PMID 22107243.
  17. ↑ # http://mike2.openmethodology.org/wiki/Small_Worlds_Data_Transformation_Measure
  18. ↑ #Hillard, Robert (2010). Information-Driven Business. Wiley. ISBN 978-0-470-62577-4.
  19. ↑ #Sandberg, Oskar. "Searching in a Small World" (PDF).
  20. ↑ #Sporns, Olaf; Chialvo DR; Kaiser M; Hilgetag CC (2004). "Organization, development and function of complex brain networks". Trends Cogn Sci. 8 (9): 418–425. doi:10.1016/j.tics.2004.07.008. PMID 15350243.
  21. ↑ #Yu, Shan; D. Huang; W. Singer; D. Nikolić (2008). "A Small World of Neuronal Synchrony". Cerebral Cortex. 18 (12): 2891–2901. doi:10.1093/cercor/bhn047. PMC 2583154 Freely accessible. PMID 18400792.
  22. ↑ #Cohen, Philip. Small world networks key to memory. New Scientist. 26 May 2004.
  23. ↑ #Sara Solla's Lecture & Slides: Self-Sustained Activity in a Small-World Network of Excitable Neurons
  24. ↑ #Ponten, S.C.; Bartolomei, F.; Stam, C.J. (April 2007). "Small-world networks and epilepsy: Graph theoretical analysis of intracerebrally recorded mesial temporal lobe seizures". Clinical Neurophysiology. 118 (4): 918–927. doi:10.1016/j.clinph.2006.12.002.
  25. ↑ 引用错误：无效<ref>标签；未给name属性为a5的引用提供文字


编者推荐

书籍推荐

《网络科学导论》封面

网络科学导论第七章小世界网络模型

《网络科学导论》由汪小帆，李翔，陈关荣联袂编著，致力于系统地介绍网络科学的基本概念、思想和方法，使得具有高等数学基础的读者都能够看懂，并具备把网络科学方法用于实际网络分析的能力。为此，本书没有过多地陷入数学和物理推导，而是更为关注网络科学的思维习惯和研究方式。

课程推荐

复杂网络2020

本课程是对复杂性科学的一个概述，包含10个章节，每节都会涵盖复杂系统的一个主要概念。


集智相关文章

从复杂网络小世界、无标度、高聚类特性看新型冠状病毒肺炎

该文章基于复杂网络最基本的三大特点——小世界、无标度、高聚类，来分析新型冠状病毒肺炎这一场突如其来的灾难。



本中文词条由用户Iceblaze9527参与编译，flynn审校，张江总审校，乐多多、薄荷、许许编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=WS小世界模型&oldid=12214”