贝叶斯分类

贝叶斯决策理论

由乘法公式引出

P(AB) = P(B|A) P(A)

P(B|A) = P(AB) / P(A)

P(B|A) = P(A|B) P(B) / P(A)

对于指定对象从属于某一类别的问题从概率的角度可以理解为求P(B|A)，意思是给定A的条件，求B发生的概率。那么对于多个类别集[math]\displaystyle{ W=\{w_1,w_2,...,w_n\} }[/math]和指定的随机变量[math]\displaystyle{ x }[/math]，则有:

 [math]\displaystyle{ W = \underset{w_i}{\operatorname{argmax}}  P(w_i|x) }[/math]

求[math]\displaystyle{ x }[/math]出现在每一个[math]\displaystyle{ w_i }[/math]的概率。带入贝叶斯公式：

 [math]\displaystyle{ 
  P(w_i|x)=\frac{p(x|w_i)P(w_i)}{p(x)}
   }[/math]

其中：

 [math]\displaystyle{ P(w_i|x) }[/math]    后验概率，即所求结果。
 [math]\displaystyle{ P(w_i) }[/math]       先验概率，可以通过训练样本直接求出。
 [math]\displaystyle{ p(x|w_i) }[/math]     随机变量[math]\displaystyle{ x }[/math]的条件概率密度函数。
 [math]\displaystyle{ p(x) }[/math]        随机变量[math]\displaystyle{ x }[/math]的概率密度函数，可通过全概率公式求出，但对于在给定的[math]\displaystyle{ x }[/math]，不影响比较[math]\displaystyle{ P(w_i|x) }[/math]的结果,可以忽略不求。

从上式看出后验概率[math]\displaystyle{ P(w_i|x) }[/math]的求解取决于对x的条件概率密度函数[math]\displaystyle{ p(x|w_i) }[/math]的估计。

朴素贝叶斯

因为x的条件概率密度函数[math]\displaystyle{ p(x|w_i) }[/math]并不容易求得，也因如果在特定场合里，给定的样本集合是离散形式的数据，这样我们将求x的条件概率密度函数[math]\displaystyle{ p(x|w_i) }[/math]变为求解条件概率[math]\displaystyle{ P(x|w_i) }[/math]。

但求解有高维特征向量x的条件概率仍然很复杂。例如: n维向量的条件概率[math]\displaystyle{ P(x_1,x_2,...,x_n|w_i) }[/math]

    [math]\displaystyle{ P(x_1,x_2,...,x_n|w_i) }[/math]
 [math]\displaystyle{ =P(x_1\vert w_i) \ P(x_2,\dots,x_n\vert w_i, x_1) }[/math]
 [math]\displaystyle{ =P(x_1\vert w_i) \ P(x_2\vert w_i, x_1) \ P(x_3,\dots,x_n\vert w_i, x_1, x_2) }[/math]
 [math]\displaystyle{ =P(x_1\vert w_i) \ P(x_2\vert w_i, x_1) \ P(x_3\vert w_i, x_1, x_2) \ P(x_4,\dots,x_n\vert w_i, x_1, x_2, x_3) }[/math]
 [math]\displaystyle{ =P(x_1\vert w_i) \ P(x_2\vert w_i, x_1) \ P(x_3\vert w_i, x_1, x_2) \ ,\dots, P(x_n\vert w_i, x_1, x_2, x_3,\dots,x_{n-1}). }[/math]

这样求解方法将随着n的增长使计算量直线上升，带来维数灾难的问题。

如果假设每个特征相互独立，那么将条件概率P(x|w_j)等于每个特征在类w_j下的条件概率P(x_i|w_j)的连乘

 [math]\displaystyle{ P(x|w_i) = \prod_{j=1}^n P(x_j|w_i) }[/math]

因为事件独立性的前提假设，这样的数据环境其实服从伯努利分布，在通常情况下每个特征取值为二值，即[math]\displaystyle{ x_j \in \{0,1\} }[/math]，即特征在一个样例中出现或者不出现。

最终朴素贝叶斯模型如下：

 [math]\displaystyle{ P(w_i|x) \varpropto P(w_i) \prod_{j=1}^n P(x_j|w_i) }[/math]
 [math]\displaystyle{ W = \underset{w_i}{\operatorname{argmax}} \ P(W=w_i) \displaystyle\prod_{j=1}^n P(X_j=x_j\vert W=w_i) }[/math]

我们以上是依据事件独立性的假设来推出朴素贝叶斯模型，但也可以从高斯分布下的贝叶斯决策准则出发，通过最大后验概率估计(MAP)推导求出（下面再谈）。

朴素贝叶斯模型是生成模型，通过学习联合概率[math]\displaystyle{ P(x_j,w_i) }[/math]来求出分类结果。它因长相朴实，实现简单所以被广大群众喜闻乐见，但因独立性假设的前置条件，使得它在特征相互依赖的复杂的数据环境下并不适用。

高斯判别分析

高斯分布

在实践中，最常遇到的概率密度函数是高斯分布，如果不能判断现实数据环境的分布情况，也可以依据中心极限定理假设其概率密度函数近似服从高斯分布。

单变量高斯函数定义为:

 [math]\displaystyle{ 
    p(x)=\frac{1}{\sqrt{2 \pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})
   }[/math]

其中，[math]\displaystyle{ \mu }[/math]为[math]\displaystyle{ x }[/math]均值，[math]\displaystyle{ \sigma^2 }[/math]为[math]\displaystyle{ x }[/math]的方差，表示[math]\displaystyle{ x }[/math]服从均值为[math]\displaystyle{ \mu }[/math]的方差为[math]\displaystyle{ \sigma^2 }[/math]的高斯分布，写为[math]\displaystyle{ p(x) \sim N(\mu, \sigma^2) }[/math]。服从高斯分布的样本聚集于均值附近，其散布程度与标准差[math]\displaystyle{ \sigma }[/math]有关。

在d维特征空间中，多元高斯函数定义为:

 [math]\displaystyle{ 
    p(x)=\frac{1}{(2 \pi)^{d/2} |\Sigma|^{1/2}}exp(-\frac{1}{2} (x-\mu)^T \Sigma^{-1}({x-\mu}))
   }[/math]

其中:

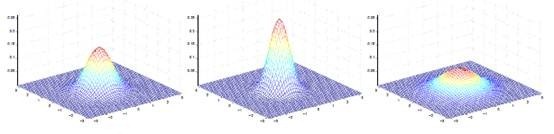
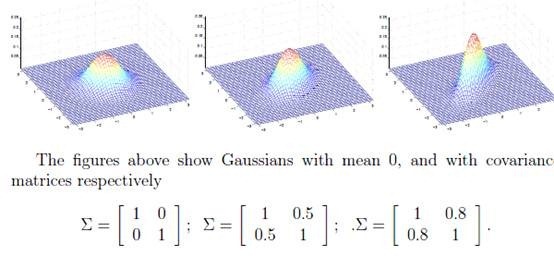
 [math]\displaystyle{ \mu }[/math]            为[math]\displaystyle{ x }[/math]d维均值向量
 [math]\displaystyle{ \Sigma }[/math]            是d*d的协方差矩阵。定义为:[math]\displaystyle{ \Sigma=E[(x-\mu)(x-\mu)^T] }[/math]。
 [math]\displaystyle{ |\Sigma| }[/math]           表示行列式的值
 [math]\displaystyle{ \Sigma^{-1} }[/math]          表示矩阵的逆
 [math]\displaystyle{ (x-\mu)^T }[/math]    是[math]\displaystyle{ (x-\mu) }[/math]的转置

协方差矩阵的相关性

[math]\displaystyle{ \sigma_{ij} }[/math]是协方差矩阵[math]\displaystyle{ \Sigma }[/math]的第ij个元素，表示随机向量的任两个维度的相关度，那么：[math]\displaystyle{ \sigma_{ij} = E[(X_i - \mu_i)(X_j - \mu_j)] }[/math]

协方差矩阵有如下特性：

• 为了使[math]\displaystyle{ |\Sigma| }[/math]的值是一个正数，我们严格限定[math]\displaystyle{ \Sigma }[/math]是正定的。

• 协方差[math]\displaystyle{ \Sigma }[/math]是对称的，其主对角线上的元素是方差，其它为协方差。

 [math]\displaystyle{ \sigma_{ij} \ge 0 }[/math]  表示第i列特征和第j列特征正相关
 [math]\displaystyle{ \sigma_{ij} \le 0 }[/math]  表示第i列特征和第j列特征负相关
 [math]\displaystyle{ \sigma_{ij} = 0 }[/math]  表示第i列特征和第j列特征不相关

• 其中均值决定中心位置(方位和高度)，协方差决定决定投影椭圆的形状(朝向和大小)。

 若方差[math]\displaystyle{ \sigma_{i}^2 \gt  \sigma_{j}^2 }[/math]，则椭圆投影向x_i轴拉伸，方差越小越陡峭
 若协方差[math]\displaystyle{ \sigma_{ij} \gt  0 }[/math]，则投影沿主对角线拉伸
 若协方差[math]\displaystyle{ \sigma_{ij} \lt  0 }[/math]，则投影沿副对角线拉伸

• 我们可以根据协方差矩阵计算任两个维度之间取值为(-1,1)之间的相关系数。

 [math]\displaystyle{ corr(X_i, X_j)= \frac{\sigma_{ij}}{\sigma_i \sigma_j},  i,j=1,2,...,d }[/math]

• 也可以根据样本协方差矩阵推导出皮尔逊相关系数，计算任两个样本之间的相关系数。

 [math]\displaystyle{ corr(x_i, x_j) = \frac{\sum_{t=1}^d (x_{it} - \overline{x_i}) (x_{jt} - \overline{x_j})}{\sqrt{\sum_{t=1}^d (x_{it} - \overline{x_i}) ^ 2} \sqrt{\sum_{t=1}^d (x_{jt} - \overline{x_j}) ^ 2}},  i,j=1,2,...,N }[/math]

多元高斯假设

从贝叶斯公式可以看出对条件概率密度函数[math]\displaystyle{ p(x|w_i) }[/math]的计算至关重要。在一些问题中，我们能够确定条件概率密度函数的类型，也就是得知他服从某一概率分布，那么问题就变成模型已知参数未知的估计问题。我们假设条件概率密度函数[math]\displaystyle{ p(x|w) }[/math]服从高斯分布，则有

 [math]\displaystyle{ p(w)=\phi^{w}(1-\phi)^{1-w} }[/math]
 [math]\displaystyle{ p(x|w=i)=p(x;\mu_i,\Sigma)=\frac{1}{(2 \pi)^{d/2} |\Sigma|^{1/2}}exp(-\frac{1}{2} (x-\mu_i)^T \Sigma^{-1}({x-\mu_i})) }[/math]

最大似然估计如下：

 [math]\displaystyle{ l(\phi,\mu_i,\Sigma)=log\prod_{j=1}^m p(x^{(j)},w^{(j)};\phi,\mu_i,\Sigma)
 }[/math]
 [math]\displaystyle{ l(\phi,\mu_i,\Sigma)=log\prod_{j=1}^m p(x^{(j)}|w^{(j)};\mu_i,\Sigma)p(w^{(j)};\phi)
 }[/math]

最大似然估计的解法是根据待估参数对似然函数求偏导，再使偏导等于0后求极致得到参数的式子，在高斯分布中，最大似然估计出来的参数等价于样本的均值和方差，这里略去证明，直接得到结果为：

 [math]\displaystyle{ \phi=\frac{1}{m}\sum_{j=1}^{m}L\{w^{(j)}=i\} }[/math]
 [math]\displaystyle{ \mu_i=\frac{\sum_{j=1}^mL\{w^{(j)}=i\}x^{(j)}}{\sum_m^{j=1}L\{w^{(j)}=i\}} }[/math]
 [math]\displaystyle{ \Sigma=\frac{1}{m}\sum_{j=1}^m(x^{(j)}-\mu_{w(j)})(x^{(j)}-\mu_{w(j)})^T }[/math]

判别分析

如果我们将P(Y|X)=P(X|Y)P(Y)使用判别函数g_i(x)获得:

 [math]\displaystyle{ g_i(x)=-\frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)-\frac{d}{2}ln2\pi-\frac{1}{2}ln|\Sigma_i|+lnP(w_i)+w_{i0} }[/math]

我们分情况讨论这个式子以简化函数

情况1：特征独立假设[math]\displaystyle{ \Sigma_i=\sigma^2I }[/math]

如果有样本数据的各特征统计独立，并且每个特征具有显通的方差[math]\displaystyle{ \sigma^2 }[/math]时，在这样的情况下协方差矩阵仅仅是[math]\displaystyle{ \sigma^2 }[/math]与单位矩阵I的乘积，为对角矩阵。几何上，它的样本数据落于同等大小的超椭球体，这样上式中的[math]\displaystyle{ |\Sigma_i| }[/math]与[math]\displaystyle{ (d/2)ln2\pi }[/math]对于任意g_i(x)都相等，可以省略。因此我们可以得到

 [math]\displaystyle{ g_i(x)=-\frac{||x-\mu_i||^2}{2\sigma^2}+lnP(w_i) }[/math]

其中[math]\displaystyle{ ||x-\mu_i||^2 }[/math]是欧几里德范数，展开就是关于x的二次函数，但实际上关于i的协方差矩阵相等，所以没必要计算，使它变成了可省略计算的常量，于是，我们得到线型判别函数：

 [math]\displaystyle{ g_i(x)=w_i^Tx+w_{i0} }[/math]
 [math]\displaystyle{ w_i=\frac{1}{\sigma^2}\mu_i }[/math]
 [math]\displaystyle{ w_{i0}=\frac{-1}{2\sigma^2}\mu_i^T\mu_i+lnP(w_i) }[/math]

情况2：同方差假设[math]\displaystyle{ \Sigma_i=\Sigma }[/math]

当所有类的协方差矩阵均相当，各自均值向量任意，几何上，样本落在相同大小和相同形状的超椭球体聚类中，第i类的聚类中心在向量[math]\displaystyle{ \mu_i }[/math]附近，式中的[math]\displaystyle{ |\Sigma_i| }[/math]与[math]\displaystyle{ (d/2)ln2\pi }[/math]对于任意g_i(x)都相等，可以省略。

 [math]\displaystyle{ g_i(x)=-\frac{1}{2}(x-\mu_i)^T\Sigma^{-1}(x-\mu_i)+lnP(w_i) }[/math]

与情况1同方差假设不同的是，样本数据各个统计特征不独立，图形投影不是正圆，点到判决函数的距离由欧式距离退化到马式距离(Mahalanobis)[math]\displaystyle{ d_m=[(x-\mu_i)^T\Sigma^-1(x-\mu_i)]^{1/2} }[/math]

 [math]\displaystyle{ g_i(x)=w_i^Tx+w_{i0} }[/math]
 [math]\displaystyle{ w_i=\Sigma^{-1}\mu_i }[/math]
 [math]\displaystyle{ w_{i0}=-\frac{1}{2}\mu_i^T\Sigma^{-1}\mu_i+lnP(w_i) }[/math]

情况3：高斯假设[math]\displaystyle{ \Sigma_i= }[/math]任意

一般的多元高斯分布，每一类的协方差矩阵是不同的，唯一可以去掉的一项是[math]\displaystyle{ (d/2)ln2\pi }[/math]，其判别函数显然是二次型。在两类问题中，对应的判定面是超二次曲面，可以是超平面，超平面对，超球体，超椭球体，超抛物面，超双曲面等各种二次曲面。

 [math]\displaystyle{ g_i(x)=X^TW_ix+w_i^Tx+lnP(w_i) }[/math]
 [math]\displaystyle{ W_i=-\frac{1}{2}\Sigma_i^{-1} }[/math]
 [math]\displaystyle{ w_i=\Sigma_i^{-1}\mu_i }[/math]
 [math]\displaystyle{ w_{i0}=-\frac{1}{2}\mu_i^T\Sigma^{-1}\mu_i-\frac{1}{2}|\Sigma_i|+lnP(w_i) }[/math]