“蝴蝶效应 Butterfly effect”的版本间的差异
(→数学定义) |
(→数学定义) |
||
| 第65行: | 第65行: | ||
我们一般在欧式空间Euclidean space或希尔伯特空间Hilbert space中考虑动力系统,这两种空间均为度量空间。 | 我们一般在欧式空间Euclidean space或希尔伯特空间Hilbert space中考虑动力系统,这两种空间均为度量空间。 | ||
| − | 考虑度量空间<math>(M,d)</math>中动力系统<math>f^t:M \to M</math>,其把初始状态<math>x_0\in M</math>映射为$t>0$时刻的系统状态<math>x_t\in M</math>。动力系统的初始条件敏感依赖性被 | + | 考虑度量空间<math>(M,d)</math>中动力系统<math>f^t:M \to M</math>,其把初始状态<math>x_0\in M</math>映射为$t>0$时刻的系统状态<math>x_t\in M</math>。动力系统的初始条件敏感依赖性被<ref>Devaney, R. (2003). An introduction to chaotic dynamical systems. Westview press.</ref>定义为,存在正数<math>\delta >0</math> 满足:对于任意 <math>x\in M</math>以及<math>x</math>的任意邻域<math>N(x)</math>都存在<math>t\geq 0</math>以及<math>y\in N(x)</math> 满足: |
<math>d(f^t(x),f^t(y))>\delta</math>. | <math>d(f^t(x),f^t(y))>\delta</math>. | ||
| 第78行: | 第78行: | ||
由此我们可以得知,初始条件敏感依赖性,并没有约束系统的长期行为是不是趋近于某一平衡态或者周期轨道;而仅仅要求了,任意从任意两个任意接近的初始状态出发,系统的两条演化轨迹在一定时间内快速分开。 | 由此我们可以得知,初始条件敏感依赖性,并没有约束系统的长期行为是不是趋近于某一平衡态或者周期轨道;而仅仅要求了,任意从任意两个任意接近的初始状态出发,系统的两条演化轨迹在一定时间内快速分开。 | ||
| − | 于是,对于具有初始条件敏感依赖性的系统(如天气系统),由于无法完全准确地测量和初始条件,以及仿真计算系统的演化,因此我们难以进行超过特定时间范围的预测,例如对于天气预测暂时无法超过一个月。不仅如此,李雅普诺夫指数还反映出,误差在一定范围内是指数增加的。这也意味着,只有我们的测量精度和计算精度指数增长,我们能预测的时长才只能线性增长。参阅 | + | 于是,对于具有初始条件敏感依赖性的系统(如天气系统),由于无法完全准确地测量和初始条件,以及仿真计算系统的演化,因此我们难以进行超过特定时间范围的预测,例如对于天气预测暂时无法超过一个月。不仅如此,李雅普诺夫指数还反映出,误差在一定范围内是指数增加的。这也意味着,只有我们的测量精度和计算精度指数增长,我们能预测的时长才只能线性增长。参阅<ref>Strogatz, S. H. (2018). Nonlinear dynamics and chaos with student solutions manual: With applications to physics, biology, chemistry, and engineering. CRC press.</ref>的例子,以及<ref>Lighthill, M. J. (1986). The recently recognized failure of predictability in Newtonian dynamics. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 407(1832), 35-50.</ref>中的精彩讨论。 |
| − | 当然,对于既不发散也不收敛、初始条件敏感、非周期变化、确定性混沌系统而言,这样的误差一般不是无限指数增加的,而是会有个限度。对于存在奇怪吸引子 strange attractor的混沌系统,例如洛伦茨发现的系统 | + | 当然,对于既不发散也不收敛、初始条件敏感、非周期变化、确定性混沌系统而言,这样的误差一般不是无限指数增加的,而是会有个限度。对于存在奇怪吸引子 strange attractor的混沌系统,例如洛伦茨发现的系统<ref>Tucker, W. (1999). The Lorenz attractor exists. Comptes Rendus de l'Académie des Sciences-Series I-Mathematics, 328(12), 1197-1202.</ref>,其最大误差不会大于奇怪吸引子的直径。对于给定动力系统的李雅普诺夫指数计算<ref> Strogatz, S. H. (2018). Nonlinear dynamics and chaos with student solutions manual: With applications to physics, biology, chemistry, and engineering. CRC press.</ref>。 |
== 洛伦茨系统演化的仿真图示 == | == 洛伦茨系统演化的仿真图示 == | ||
2020年12月16日 (三) 16:52的最新版本
历史
美国气象学家爱德华·洛伦茨 Edward N. Lorenz 1963年在一篇发表于《大气科学杂志》 Journal of Atmospheric Sciences的论文《确定性非周期流》Deterministic Nonperiodic Flow[1]中首次观察并分析了这个效应,并在发表于《纽约科学院学报》 Transactions of the New York Academy of Sciences 的论文《流体动力流的可预测性》The Predictability of Hydrodynamic Flow 中评论说:“一个气象学家曾评论说:'如果这个理论是正确,那么海鸥扇动一次翅膀就足以永远改变天气变化。'在后来的演讲和论文中他用了更加有诗意的表达——"蝴蝶效应"。
对于这个效应最常见的阐述是:"一只南美洲亚马逊河流域热带雨林中的蝴蝶,偶尔扇动几下翅膀,可以在两周以后引起美国得克萨斯州的一场龙卷风。"
其原因就是蝴蝶扇动翅膀的运动,蝴蝶的这一动作,影响了它周围的微弱气流,从而微弱地改变了,“天气变化”这一动态过程,导致其身边的空气系统发生变化,并产生微弱的气流,而微弱气流的产生又会引起四周空气或其他系统产生相应的变化,由此引起一个连锁反应,最终导致其他系统的极大变化。一般来说,微观尺度上蝴蝶微弱的干扰,不会影响宏观尺度上整个天气变。然而,在某些情况下,正好是蝴蝶多扇动了一次翅膀所造成的微观效果,由此引起了连锁反应,随后在天气的变化中不断扩大自身,乃至于后来成为龙卷风这样宏观尺度的天气现象。洛伦茨在利用数值工具预测天气变化时,观察到了这样的效应。他发现,将天气模型的初始条件进行看似无关紧要的四舍五入之后,模型所预测的天气变化完全不同于四舍五入之前所预测的那样。实际上,这种现象曾在数学和科学历史上被反复发现过,至少追溯到麦克斯韦 James Clerk Maxwell 和庞加莱 Henri Poincaré ,但是一直没有引起学术界足够的重视,直到1972年,洛伦兹在一场于华盛顿召开的学术会议上,做了那场著名的演讲,题为《可预测性:在巴西的一只蝴蝶扇扇翅膀会引起在特克萨斯州的龙卷风吗》Predictability: Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?。在此之后,蝴蝶效应以及这个现象背后的原理开始引起学术界的广泛关注。1975年,李天岩Tien-Yien Li 和詹姆斯·约克 James Yorke’s 发表了题为《周期三意味着混沌》Period three implies chaos,正式使用了混沌一词来命名这个领域的研究。随着之后混沌理论的发展,"蝴蝶效应"这个形象又生动的比喻逐渐广为人知 —— 一个不起眼的小动作却有可能会引起一连串的巨大反应。
概念
混沌理论中的蝴蝶效应
在混沌理论 chaos theory 中,蝴蝶效应指的是动力系统 dynamical system 的一种属性,即其关于初始条件的敏感依赖性 the sensitive dependence on initial conditions 。对于具备这种属性的确定性动力系统 deterministic system, 某个状态量的微小改变都有可能导致这个系统之后演化过程的巨大差异。
根据 Gleick (2011) 的考证,“初始条件的敏感依赖性“并不是个全新的概念,之前人们所传颂的谚语中就有提到:
丢了一只马蹄铁,折了一匹战马;
折了一匹战马,损了一位国王;
损了一位国王,输了一场战争;
输了一场战争,亡了一个帝国。
For want of a nail, the shoe was lost;
For want of a shoe, the horse was lost;
For want of a horse, the rider was lost;
For want of a rider, the battle was lost;
For want of a battle, the kingdom was lost!
看起来丢了一只马蹄跌只是一件无关痛痒的小事,但是在事物发展过程中,这却有可能导致完全无法预知的大后果。
蝴蝶效应反映了事物发展经常同时存在“定数”与“变数”,事物在发展过程中其发展轨迹有规律可循,同时也可能被不可预知、不可精确测量的“变数”所影响。这样使得我们即使已经掌握了确定的规律,但是在根据规律而做预测和推断时,也有可能会失之毫厘,差之千里。微观上的一个小变化却有可能影响宏观上事物的大发展,这反映了一些事物的发展具有复杂性。
蝴蝶效应的成因分析
如前文所说,蝴蝶效应指的是动力系统的初始条件敏感依赖性,那么什么样的动力系统会有这样的性质?
最简单的情况就是发散的divergent动力系统。例如削尖的铅笔,其笔尖立在桌子上。理论上它可以保持平衡,但是非常不稳定,稍微一点外力影响就会倒下。如果我们不考虑在铅笔倒下过程中,桌子对铅笔的阻挡作用,那么铅笔倒下之后,就会一直跌落下去,直到无穷远。这个时候我们说,铅笔动力系统的运动轨迹发散到了无穷。这样的铅笔动力系统就是发散的。从过程角度来说,发散的动力系统都具有初始条件敏感依赖性,只要初始条件有一点差异,那么系统的演化过程就会很不一样;从“结果”(长期行为)角度来说,发散的动力系统都不具备初始条件敏感依赖性,因为无论什么样的初始条件,系统的演化过程一定是朝向无穷大(或无穷远)的。
除了发散的动力系统之外,还有一些介于收敛convergent和发散之间的动力系统,会具备初始条件的敏感依赖性。
这类系统又可以分成三类,第一类是含有鞍点saddle point平衡态的系统。和上面说的发散系统不同,对于含有鞍点的系统,当初始条件在鞍点附近的某些区域,系统演化会趋向于鞍点平衡态,而在鞍点附近的另一些区域,系统演化会远离于鞍点平衡态。
第二类是具有多个平衡态和周期态的系统,例如范德波尔振荡器 van der Pol Oscillator。这种振荡器是荷兰物理学家 Balthasar van der Pol 在1927年研究真空管时首次提出的动力系统。对于这种系统来说,当系统初始状态在某一区域时,系统状态先发散,之后的长期行为趋近于周期变化,而系统初始状态在另外一些区域时,系统状态不经发散直接趋于周期变化。如果改变这个动力系统的参数,又会出现,当系统初始状态在某一区域时,系统状态收敛到某一平衡态,而在另一区域时,系统状态又趋于无穷。隧道二极管 tunnel diode 动力系统也有类似的性质。
第三类就是混沌系统,例如洛伦茨所构建的系统。这类系统不仅具备初始条件敏感依赖性,而且既不发散,也不收敛,还表现出非周期aperiodic/nonperiodic现象。狭义的说,洛伦茨所考虑的蝴蝶效应,正是混沌系统的效应。但是严格的说,初始条件敏感依赖性,并不是混沌系统的专有性质。只是在20世纪60年代,人们对于混沌的认识不深,因此把蝴蝶效应定义为了初始条件敏感依赖性,而没有注意区分蝴蝶效应和混沌行为。
今天,我们一般所说的蝴蝶效应,也主要指混沌系统的初始条件敏感依赖性(Shinbrot et al., 1992)。然而,我们不应混淆蝴蝶效应和混沌系统。虽然混沌系统都具备这样的性质,但是具备这样性质的系统,却不一定是混沌系统。[2]
数学定义
动力系统理论是数学的分支,动力系统的初始条件敏感依赖性自然就是一个数学性质。数学上,为了保持一般性,我们在度量空间中考虑动力系统的初始条件敏感依赖性。
考虑度量空间[math]\displaystyle{ (M,d) }[/math],[math]\displaystyle{ M }[/math]是集合,[math]\displaystyle{ d:M \times M \to \mathbb R }[/math]是定义[math]\displaystyle{ M }[/math]上的二元函数,[math]\displaystyle{ \forall x,y,z\in M }[/math]其满足
- [math]\displaystyle{ d(x,y)\geq 0 }[/math], [math]\displaystyle{ d(x,y)=0 }[/math]当且仅当 [math]\displaystyle{ x=y }[/math] (正定性)
- [math]\displaystyle{ d(x,y) = d(y,x) }[/math] (对称性)
- [math]\displaystyle{ d(x,z)\leq d(x,y)+d(y,z) }[/math] (三角不等式)
我们一般在欧式空间Euclidean space或希尔伯特空间Hilbert space中考虑动力系统,这两种空间均为度量空间。
考虑度量空间[math]\displaystyle{ (M,d) }[/math]中动力系统[math]\displaystyle{ f^t:M \to M }[/math],其把初始状态[math]\displaystyle{ x_0\in M }[/math]映射为$t>0$时刻的系统状态[math]\displaystyle{ x_t\in M }[/math]。动力系统的初始条件敏感依赖性被[3]定义为,存在正数[math]\displaystyle{ \delta \gt 0 }[/math] 满足:对于任意 [math]\displaystyle{ x\in M }[/math]以及[math]\displaystyle{ x }[/math]的任意邻域[math]\displaystyle{ N(x) }[/math]都存在[math]\displaystyle{ t\geq 0 }[/math]以及[math]\displaystyle{ y\in N(x) }[/math] 满足: [math]\displaystyle{ d(f^t(x),f^t(y))\gt \delta }[/math].
这里的中心思想是,只要动力系统对于任意初始状态[math]\displaystyle{ x }[/math],存在一个任意接近$x$的系统状态量[math]\displaystyle{ y }[/math],它能逐渐演化远离[math]\displaystyle{ x }[/math],那么这个动力系统就具备初始条件的敏感依赖性。这里要强调,没有必要要求[math]\displaystyle{ x }[/math]附近的所有[math]\displaystyle{ y }[/math]都最终[math]\displaystyle{ f^t(y) }[/math]不趋近[math]\displaystyle{ f^t(x) }[/math];只要至少有一个这样的[math]\displaystyle{ y }[/math]就可以了。
如果对于[math]\displaystyle{ x }[/math]附近的所有[math]\displaystyle{ y }[/math]都满足,最终[math]\displaystyle{ f^t(y) }[/math]不趋近[math]\displaystyle{ f^t(x) }[/math],那么我们称这个系统具有扩张性(expansiveness)我们也用李雅普诺夫指数 Lyapunov exponent 来定义初始条件敏感依赖性。
考虑度量空间[math]\displaystyle{ (M,d) }[/math]中动力系统[math]\displaystyle{ f^t:M \to M }[/math],其把初始状态[math]\displaystyle{ x_0\in M }[/math]映射为[math]\displaystyle{ t\gt 0 }[/math]时刻的系统状态</math>x_t\in M</math>。动力系统的初始条件敏感依赖性被定义为,存在正数</math>\lambda >0</math> 满足:对于任意 [math]\displaystyle{ x\in M }[/math]以及[math]\displaystyle{ \delta \gt 0 }[/math]都存在满足[math]\displaystyle{ d(x,y)\lt \delta }[/math]的[math]\displaystyle{ y }[/math]以及时刻[math]\displaystyle{ t\geq 0 }[/math]满足: [math]\displaystyle{ d(f^t(x),f^t(y))\gt e^{\lambda t}d(x,y) }[/math] 这里的$\lambda$就被称为李雅普诺夫指数。我们也称具有正李雅普诺夫指数的动力系统,具有初始条件敏感依赖性。
由此我们可以得知,初始条件敏感依赖性,并没有约束系统的长期行为是不是趋近于某一平衡态或者周期轨道;而仅仅要求了,任意从任意两个任意接近的初始状态出发,系统的两条演化轨迹在一定时间内快速分开。
于是,对于具有初始条件敏感依赖性的系统(如天气系统),由于无法完全准确地测量和初始条件,以及仿真计算系统的演化,因此我们难以进行超过特定时间范围的预测,例如对于天气预测暂时无法超过一个月。不仅如此,李雅普诺夫指数还反映出,误差在一定范围内是指数增加的。这也意味着,只有我们的测量精度和计算精度指数增长,我们能预测的时长才只能线性增长。参阅[4]的例子,以及[5]中的精彩讨论。
当然,对于既不发散也不收敛、初始条件敏感、非周期变化、确定性混沌系统而言,这样的误差一般不是无限指数增加的,而是会有个限度。对于存在奇怪吸引子 strange attractor的混沌系统,例如洛伦茨发现的系统[6],其最大误差不会大于奇怪吸引子的直径。对于给定动力系统的李雅普诺夫指数计算[7]。
洛伦茨系统演化的仿真图示
洛伦茨吸引子中的蝴蝶效应 时间 0 ≤ t ≤ 30 z 坐标 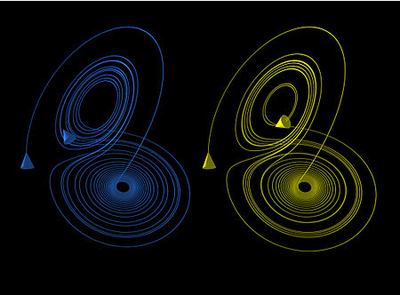
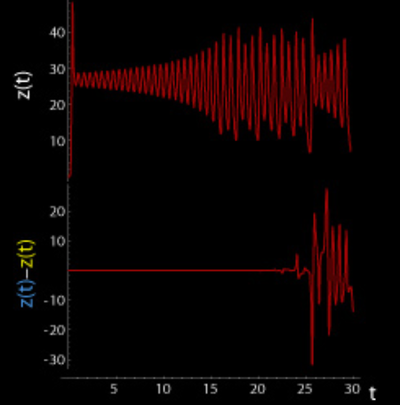
这些两幅图表示了洛伦茨系统从两个相差无几的初始状态(仅在某一方向上差[math]\displaystyle{ 10^{-5} }[/math])而演化的过程。上图中,蓝色曲线由外侧的蓝色椎体开始,演化30倍单位时间之后,到达内侧的蓝色椎体;黄色曲线由外侧的黄色椎体开始,演化30倍单位时间之后,到达内侧的黄色椎体。这里把这两条曲线分开绘制的原因是,两条曲线的大部分高度相近,若绘制在一起,则会看起来重合在一起,而不方便我们对比这两条曲线的不同。通过对比这两条曲线,我们可以发现,两条演化轨迹在最后一段时间完全不同,特别是最终位置明显差了一截。 下图对比了两条曲线的沿某一固定方向的坐标变化。其中上半子图是两条曲线的平均坐标变化,下半子图是两条曲线坐标差异的变化。可以看出,最初,两条轨迹几乎是重合的,而当演化时间超过23倍单位时间的时候,两条演化曲线开始不再一致,并且他们的差异开始无规律震荡,到最终30倍单位时间时,两条曲线大概相差15倍单位坐标。 由此可见,初始条件的微小不同(仅在某一方向上差[math]\displaystyle{ 10^{-5} }[/math]倍单位坐标),在经过30倍单位时间的演化后,放大了10万倍,成了巨大的差异(15倍单位坐标)
洛伦茨吸引子的动画显示了不断的发展。
各领域中的蝴蝶效应
天气系统方面
蝴蝶效应在气象领域是最为人所熟知的,例如标准天气预报模型就可以轻而易举地的演示这一效应。气候科学家詹姆斯·安南 James Annan和威廉·康诺利 William Connolley解释说,混沌对天气预报方法的发展很重要; 天气模型对初始条件很敏感。 他们也补充告诫: “当然,是否有一只未知蝴蝶扇动翅膀不会直接显示在天气预报上,因为这样一个微小的扰动需要很长时间才会发展到一个显著的规模,而且还有许多更直接的不确定因素需要我们担心。因此,如果说蝴蝶效应这一现象直接对天气预报造成了什么影响,这一说法往往在某种程度上是错误的。”[8]
量子力学方面
一些学者已经论证了,量子力学系统中不存在"初始条件的极端(指数)敏感依赖性",但是量子系统能以一些量子现象反映经典力学中的混沌现象(通过考虑随机矩阵的特征值)。随机矩阵理论和基于量子计算机的仿真也验证了在量子力学中不存在蝴蝶效应(Sinitsyn and Yan, 2020)。[9][10] 一些作者认为,在纯量子处理中不存在对初始条件的极端(指数)依赖;[11][12]然而,经典运动证明了系统对初始条件存在敏感依赖,Martin Gutzwiller[13]、Delos 及其同事发展的半经典处理也纳入了这一点。[14]
也有其他学者认为,如果我们换个角度,也可以在量子系统中可以观测到某种演化过程的敏感性,类似经典力学中的蝴蝶效应。在经典力学中,我们所讨论的蝴蝶效应,是对于给定的哈密顿主函数(系统动力学方程),考虑受微扰的系统状态量,从而观察到了系统状态量在微扰作用后的演化差异。而在量子力学中,系统状态量是波函数,并不存在相对于时间的状态发散。于是这些学者考虑,我们在量子力学中,我们固定系统初始状态量,而考虑受微扰的哈密顿主函数,再观察系统状态量的演化差异(Peres, 2006)。从这个方面考虑,卡库谢夫斯基 Karkuszewski 等学者,以系统状态量的重叠程度作为"标度"measure,研究了对于同一初始状态,不同哈密顿量的敏感性水平。这一视角是思考量子混沌的一条路径,不过基本上不被算作量子力学版本的蝴蝶效应。[15][16]这种量子蝴蝶效应已被实验证实。[17]量子和半经典处理的系统对初始条件的敏感性被称为量子混沌。[11][15]
中国古籍中的蝴蝶效应
《吕氏春秋·察微》原文:
楚之边邑曰卑梁,其处女与吴之边邑处女桑于境上,戏而伤卑梁之处女。卑梁人操其伤子以让吴人,吴人应之不恭,怒,杀而去之。吴人往报之,尽屠其家。卑梁公怒,曰:“吴人焉敢攻吾邑?”举兵反攻之,老弱尽杀之矣。吴王夷昧闻之,怒,使人举兵侵楚之边邑,克夷而后去之。
吴、楚以此大隆。吴公子光又率师与楚人战于鸡父,大败楚人,获其帅潘子臣、小帷子、陈夏啮。又反伐郢,得荆平王之夫人以归,实为鸡父之战。凡持国,太上知始,其次知终,其次知中。三者不能,国必危,身必穷。
《孝经》曰:“高而不危,所以长守贵也;满而不溢,所以长守富也。富贵不离其身,然后能保其社稷,而和其民人。”楚不能之也。
译文:
楚国有个边境城邑叫卑梁,那里的姑娘和吴国边境城邑的姑娘同在边境上采桑叶,游戏时,吴国的姑娘弄伤了卑梁的姑娘。卑梁的人带着受伤的姑娘去责备吴国人。吴国人出言不恭,卑梁人十分恼火,杀死吴人走了。吴国人去卑梁报复,把那个卑梁人全家都杀了。
卑梁的守邑大夫大怒,说:“吴国人怎么敢攻打我的城邑?”于是发兵反击吴人,把吴人老幼全都杀死了。吴王夷昧听到这件事后很生气,派人领兵入侵楚国的边境城邑,攻占夷以后才离去。吴国和楚国因此发生了大规模的冲突。吴国公子光又率领军队在鸡父和楚国人交战,大败楚军,俘获了楚军的主帅潘子臣、小帷子以及陈国的大夫夏啮。又接着攻打郢都,获得楚平王的夫人而回。这就是鸡父之战。凡是主持国事,最上等的是要了解事情开始时的情势,其次是要预见到事情的结局,再次是要知道事情发展的经过。这三点都做不到,国家一定危险,自身一定困窘。
《孝经》上说:“高却不倾危,就能长期保持尊贵;满却不外溢,就能长期保持富足。富贵不离其身,然后才能保住他的国家,而且安定他的人民。”可是楚国做不到这一点。
流行文化的引用
2008年,记者彼得·迪齐克斯 Peter Dizikes在《波士顿环球报 The Boston Globe》上撰文指出,流行文化喜欢蝴蝶效应这个概念,但却把它搞错了。相比于洛伦茨用蝴蝶的隐喻正确地指出了可预测性“本质上是有限的” ,流行文化却假定,每一个发生的事件都可以由寻找引起它的基本条件来进行解释。 迪齐克斯解释说: “这说明了我们更大的期望,那就是这个世界应该是可以理解的 —— 也就是每件事的发生都是合理的(可以用理性去探究推理的),并且我们可以明确且准确的进行解释,无论这些解释所用的基本条件有多么细微。然而,大自然本身就漠视了这种期望”[18]
进一步阅读
- 刘式达. 从蝴蝶效应谈起[M]. 湖南教育出版社, 1994.[1]
- 韩立新, 霍江河. “蝴蝶效应”与网络舆论生成机制[J]. 当代传播, 2008(06):65-68.[2]
- 匡文波. 论新媒体传播中的“蝴蝶效应”及其对策[J]. 国际新闻界, 2009, 6(8):72-75.[3]
参考文献
- ↑ Lorenz, Edward N. (March 1963). "Deterministic Nonperiodic Flow". Journal of the Atmospheric Sciences. 20(2): 130–141.
- ↑ Shinbrot, T., Ditto, W., Grebogi, C., Ott, E., Spano, M., & Yorke, J. A. (1992). Using the sensitive dependence of chaos (the ‘‘butterfly effect’’) to direct trajectories in an experimental chaotic system. Physical review letters, 68(19), 2863.
- ↑ Devaney, R. (2003). An introduction to chaotic dynamical systems. Westview press.
- ↑ Strogatz, S. H. (2018). Nonlinear dynamics and chaos with student solutions manual: With applications to physics, biology, chemistry, and engineering. CRC press.
- ↑ Lighthill, M. J. (1986). The recently recognized failure of predictability in Newtonian dynamics. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 407(1832), 35-50.
- ↑ Tucker, W. (1999). The Lorenz attractor exists. Comptes Rendus de l'Académie des Sciences-Series I-Mathematics, 328(12), 1197-1202.
- ↑ Strogatz, S. H. (2018). Nonlinear dynamics and chaos with student solutions manual: With applications to physics, biology, chemistry, and engineering. CRC press.
- ↑ "Chaos and Climate". RealClimate. Archived from the original on 2014-07-02. Retrieved 2014-06-08.
- ↑ Heller, E. J.; Tomsovic, S. (July 1993). "Postmodern Quantum Mechanics". Physics Today. 46 (7): 38–46. Bibcode:1993PhT....46g..38H. doi:10.1063/1.881358.
- ↑ Gutzwiller, Martin C. (1990). Chaos in Classical and Quantum Mechanics. New York: Springer-Verlag. ISBN 0-387-97173-4.
- ↑ 11.0 11.1 Rudnick, Ze'ev (January 2008). "What is...Quantum Chaos" (PDF). Notices of the American Mathematical Society. Archived (PDF) from the original on 2009-10-02.
- ↑ Berry, Michael (1989). "Quantum chaology, not quantum chaos". Physica Scripta. 40 (3): 335–336. Bibcode:1989PhyS...40..335B. doi:10.1088/0031-8949/40/3/013.
- ↑ Gutzwiller, Martin C. (1971). "Periodic Orbits and Classical Quantization Conditions". Journal of Mathematical Physics. 12 (3): 343. Bibcode:1971JMP....12..343G. doi:10.1063/1.1665596.
- ↑ Gao, J.; Delos, J. B. (1992). "Closed-orbit theory of oscillations in atomic photoabsorption cross sections in a strong electric field. II. Derivation of formulas". Physical Review A. 46 (3): 1455–1467. Bibcode:1992PhRvA..46.1455G. doi:10.1103/PhysRevA.46.1455. PMID 9908268.
{{cite journal}}: Unknown parameter|lastauthoramp=ignored (help) - ↑ 15.0 15.1 Poulin, David. "A Rough Guide to Quantum Chaos" (PDF). Archived from the original (PDF) on 2010-11-04.
- ↑ Peres, A. (1995). Quantum Theory: Concepts and Methods. Dordrecht: Kluwer Academic.
- ↑ Lee, Jae-Seung; Khitrin, A. K. (2004). "Quantum amplifier: Measurement with entangled spins". Journal of Chemical Physics. 121 (9): 3949–51. Bibcode:2004JChPh.121.3949L. doi:10.1063/1.1788661. PMID 15332940.
{{cite journal}}: Unknown parameter|lastauthoramp=ignored (help) - ↑ Dizikes, Petyer (8 June 2008). "The meaning of the butterfly". The Boston Globe. Archived from the original on 18 April 2016. Retrieved 8 June 2016.
编者推荐
集智推荐
Chaos and the Butterfly Effect
本节课程,将主要围绕逻辑斯谛方程(logistic equation),一种迭代函数,带领大家初步认识蝴蝶效应(butterfly effect),将讨论蝴蝶效应的影响,并深入探讨随机性(randomness)概念。
圣塔菲课程:Introduction to Dynamical Systems and Chaos
本课程中,主要介绍动力学系统和混沌系统,您将学到蝴蝶效应(butterfly effect)、奇异吸引子(attractors)等基本概念,以及如何应用于您感兴趣的领域。
蝴蝶效应和混沌故事 | 陈关荣
“人们经常都会看到,纯粹理论研究的一点点成果,也许在很长时间之后,会导致连做该纯理论研究的科学家都始料不及的实际应用。”
什么是动力系统理论 | 集智百科
动力系统理论 dynamical systems theory ,也常译作动力学理论、或动力系统理论,它是数学研究的一部分。它主要利用微分和差分方程,来描述和研究复杂的动力系统。
书籍推荐
《蝴蝶效应之谜:走近分形与混沌》
内容简介:有人将分形和混沌理论誉为继相对论和量子力学之后的20世纪物理学的第三次革命。本书首先描述了各种分形的基础知识和特性,包括线性迭代产生的分形如分形龙、科和曲线等,以及非线性迭代产生的曼德勃罗集、朱利亚集等。通过这些例子,介绍了自相似性及分数维的概念。然后,遵循混沌现象发展的历史,通过讲述庞加莱的三体问题、洛伦茨的蝴蝶效应等等故事和趣闻,将读者带进神奇混沌理论的天地中。再进一步通过对一个简单混沌系统--逻辑斯蒂映射的探讨,详细介绍分岔理论、稳定性、及费根鲍姆普适常数等概念。
本书后半部分,介绍了分形和混沌在各个领域的应用及前景、分形和混沌的关系、以及与分形混沌密切相关而发展起来的非线性科学。
《蝴蝶效应(知微见著,影响我们生活的,往往是从小事开始。)》
内容简介:本书剖析了以“蝴蝶效应”为代表的诸多心理学规律、法则在人们生活、工作等方面运行的心理机制:初始条件十分微小的变化经过不断放大,对其未来状态会造成极其巨大的差别。本书语言生动流畅,案例与理论鲜明而不枯燥,能帮助读者从容应对种种不可控却对生活影响至深的事件……
《蝴蝶效应 经济和社会中那些不可忽略的小事件》
内容简介:社会科学特别是经济学传统的思维方式将世界看作一部机器,虽然复杂但却可以被理解传统的经济学思维方式往往将世界看作一部机器,虽然复杂但却可以被理解甚至控制。这种思维至多只能片面地说明世界是如何运转的,而无法看到世界的本质。为什么犯罪率居高不下?为什么投资过亿的电影,票房表现却差强人意?为什么成年人中单身的比例越来越高?这些都是主流经济学没能完美地解释的问题。在本书中,作者从蚂蚁模型出发,通过大量的事例,详细地解释了蝴蝶效应在社会与经济运行中的作用。个体的品位和偏好会受到社会中其他人的影响,将这一理念加入到经济学分析中可以解释很多社会现象。本书为政府决策人、经济学学者、经济学专业学生以及对经济学感兴趣的读者提供了多元的视角、生动的案例和变革性的方法。
视频推荐
电影《蝴蝶效应》
剧情简介: 伊万(艾什顿·库奇 Ashton Kutcher 饰)曾经有一个糟糕的童年,因为他行为闯下了大祸,令他童年充满不堪回忆的往事。而事实上,他确实只是依稀记得一点可怕的情景,这些情景一直纠缠着他的正常生活。伊万接受心理学家建议,把琐碎生活记在记事本里,却偶然发现通过记事本回到过去。这时他才清楚记起,童年时候的自己做了那么多的错事。他幻想着用现在的意识,潜入童年的身体,去弥补种种过失给人们带来的伤害,尤其是希望与当年暗恋的凯西最终走回一起。然而他一次次的跨越时空的更改,只能越来越招致现实世界的不可救药。一切就像蝴蝶效应般,牵一发而动全身。
视频《什么是蝴蝶效应》
剧情简介:利用动画生动的展现了由于一只蝴蝶扇动翅膀而造成的一系列事件,从而诠释蝴蝶效应。
本中文词条由Yillia Jing参与编译,木子二月鸟审校,许许、薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。