“Lotka–Volterra方程式”的版本间的差异
| 第280行: | 第280行: | ||
{{mvar|α}} = 2/3, {{mvar|β}} = 4/3, {{mvar|γ}} = 1 = {{mvar|δ}}. 假设{{math|''x'', ''y''}}处于“千”级别还不到“万“。圆圈代表从{{mvar|x}} = {{mvar|y}} = 0.9 到 1.8时猎物和捕食者的初始条件,步长为0.1,且固定点在(1,1/2)。 | {{mvar|α}} = 2/3, {{mvar|β}} = 4/3, {{mvar|γ}} = 1 = {{mvar|δ}}. 假设{{math|''x'', ''y''}}处于“千”级别还不到“万“。圆圈代表从{{mvar|x}} = {{mvar|y}} = 0.9 到 1.8时猎物和捕食者的初始条件,步长为0.1,且固定点在(1,1/2)。 | ||
| − | ==Dynamics of the system== | + | == Dynamics of the system 系统动力学 == |
In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a cycle of growth and decline. | In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a cycle of growth and decline. | ||
| 第286行: | 第286行: | ||
In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a cycle of growth and decline. | In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a cycle of growth and decline. | ||
| − | + | 在该模型系统中,捕食者在有大量猎物的情况下肆意成长,但最终它们会因为食物供应不足而下降。随即捕食者数量变低,猎物数量将再次增加。就此形成的动力结构以增长和下降的周期持续。 | |
| 第585行: | 第585行: | ||
其中 e 是欧拉数。 | 其中 e 是欧拉数。 | ||
| − | |||
| − | |||
==See also== | ==See also== | ||
2021年1月12日 (二) 13:09的版本
此词条Jie翻译。
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
Lotka–Volterra方程式(又称为猎食方程)是一对一阶非线性微分方程,它经常被用来描述两个物种间因相互作用,而产生的生物系统动力学反应。其中一个作为捕食者,而另一个作为猎物。其人口数量会随时间变化遵循如下一对方程组:
- [math]\displaystyle{ \begin{align} \frac{dx}{dt} &= \alpha x - \beta x y, \\ \frac{dy}{dt} &= \delta x y - \gamma y, \end{align} }[/math]
Where,
- x is the number of prey (for example, rabbits);
- y is the number of some predator (for example, foxes);
- [math]\displaystyle{ \tfrac{dy}{dt} }[/math] and [math]\displaystyle{ \tfrac{dx}{dt} }[/math] represent the instantaneous growth rates of the two populations;
- t represents time;
- α, β, γ, δ are positive real parameters describing the interaction of the two species.
其中:
- x是猎物(例如兔子)的数量;
- y是某些捕食者(例如狐狸)的数量;
- [math]\displaystyle{ \tfrac{dy}{dt} }[/math] 和 [math]\displaystyle{ \tfrac{dx}{dt} }[/math]代表两个人口的瞬时增长率;
- t代表时间;
- α, β, γ, δ是描述两个物种相互作用的正实参数。
The Lotka–Volterra system of equations is an example of a Kolmogorov model,[1][2][3] which is a more general framework that can model the dynamics of ecological systems with predator–prey interactions, competition, disease, and mutualism.
The Lotka–Volterra system of equations is an example of a Kolmogorov model, which is a more general framework that can model the dynamics of ecological systems with predator–prey interactions, competition, disease, and mutualism.
Lotka–Volterra方程式系统是Kolmogorov模型的一个示例,该模型是一个更通用的框架,可以利用捕食者与猎物之间的猎食,竞争,疾病和共生关系来模拟生态系统的动力学。
History 历史
The Lotka–Volterra predator–prey model was initially proposed by Alfred J. Lotka in the theory of autocatalytic chemical reactions in 1910.[4][5] This was effectively the logistic equation,[6] originally derived by Pierre François Verhulst.[7] In 1920 Lotka extended the model, via Andrey Kolmogorov, to "organic systems" using a plant species and a herbivorous animal species as an example[8] and in 1925 he used the equations to analyse predator–prey interactions in his book on biomathematics.[9] The same set of equations was published in 1926 by Vito Volterra, a mathematician and physicist, who had become interested in mathematical biology.[5][10][11] Volterra's enquiry was inspired through his interactions with the marine biologist Umberto D'Ancona, who was courting his daughter at the time and later was to become his son-in-law. D'Ancona studied the fish catches in the Adriatic Sea and had noticed that the percentage of predatory fish caught had increased during the years of World War I (1914–18). This puzzled him, as the fishing effort had been very much reduced during the war years. Volterra developed his model independently from Lotka and used it to explain d'Ancona's observation.[12]
The Lotka–Volterra predator–prey model was initially proposed by Alfred J. Lotka in the theory of autocatalytic chemical reactions in 1910. This was effectively the logistic equation, originally derived by Pierre François Verhulst. In 1920 Lotka extended the model, via Andrey Kolmogorov, to "organic systems" using a plant species and a herbivorous animal species as an example and in 1925 he used the equations to analyse predator–prey interactions in his book on biomathematics. The same set of equations was published in 1926 by Vito Volterra, a mathematician and physicist, who had become interested in mathematical biology. Volterra's enquiry was inspired through his interactions with the marine biologist Umberto D'Ancona, who was courting his daughter at the time and later was to become his son-in-law. D'Ancona studied the fish catches in the Adriatic Sea and had noticed that the percentage of predatory fish caught had increased during the years of World War I (1914–18). This puzzled him, as the fishing effort had been very much reduced during the war years. Volterra developed his model independently from Lotka and used it to explain d'Ancona's observation.
Lotka–Volterra猎捕模型最初是由阿尔弗雷德·J·洛特卡(Alfred J. Lotka)于1910年在自催化化学反应理论中提出的。这个模型最初实际上是源于皮埃尔·弗朗索瓦·韦吕勒Pierre François Verhulst得出的逻辑方程。1920年,洛特卡通过Andrey Kolmogorov将该模型扩展到了“有机系统”,以植物和草食性动物为例,并于1925年在他的生物数学书中使用这些方程式分析了捕食者与猎物之间的相互作用。1926年,数学家和物理学家维托·沃尔泰拉Vito Volterra发表了同样的方程组。沃尔泰拉对数学生物学非常感兴趣。他对此的探索是受到他与海洋生物学家翁贝托·德安科纳Umberto D'Ancona互动的启发,后者当时正好向的女儿求婚,不久便成了他的女婿。德安科纳研究了亚得里亚海的渔获物,并注意到在第一次世界大战期间(1914-1918年),捕捞的掠食性鱼类其百分比有所增加。这使他感到困惑,因为在战争年代,捕鱼工作已大大减少。沃尔泰拉独立于洛特卡开发了他的模型,并用它来解释德安科纳的观察结果。
The model was later extended to include density-dependent prey growth and a functional response of the form developed by C. S. Holling; a model that has become known as the Rosenzweig–MacArthur model.[13] Both the Lotka–Volterra and Rosenzweig–MacArthur models have been used to explain the dynamics of natural populations of predators and prey, such as the lynx and snowshoe hare data of the Hudson's Bay Company[14] and the moose and wolf populations in Isle Royale National Park.[15]
The model was later extended to include density-dependent prey growth and a functional response of the form developed by C. S. Holling; a model that has become known as the Rosenzweig–MacArthur model. Both the Lotka–Volterra and Rosenzweig–MacArthur models have been used to explain the dynamics of natural populations of predators and prey, such as the lynx and snowshoe hare data of the Hudson's Bay Company and the moose and wolf populations in Isle Royale National Park.
该模型后来得到进一步扩展,包括基于密度依赖的猎物生长机制和由C. S. Holling开发的功能响应机制。该模型后被称为Rosenzweig–MacArthur模型。Lotka–Volterra和Rosenzweig–MacArthur模型现均用于解释捕猎双方自然种群的动态,例如哈德逊湾公司的山猫和雪鞋野兔数据,以及皇家岛国家公园的麋鹿和狼种群。
In the late 1980s, an alternative to the Lotka–Volterra predator–prey model (and its common-prey-dependent generalizations) emerged, the ratio dependent or Arditi–Ginzburg model.[16] The validity of prey- or ratio-dependent models has been much debated.[17]
In the late 1980s, an alternative to the Lotka–Volterra predator–prey model (and its common-prey-dependent generalizations) emerged, the ratio dependent or Arditi–Ginzburg model. The validity of prey- or ratio-dependent models has been much debated.
在1980年代后期,出现了Lotka–Volterra捕猎模型(泛指常规食饵依赖模型)的替代模型,即比率依赖模型或Arditi–Ginzburg模型。即使到现在。食饵依赖和比率依赖模型的有效性一直存在争议。
The Lotka–Volterra equations have a long history of use in economic theory; their initial application is commonly credited to Richard Goodwin in 1965[18] or 1967.[19][20]
The Lotka–Volterra equations have a long history of use in economic theory; their initial application is commonly credited to Richard Goodwin in 1965 or 1967.
Lotka-Volterra方程在经济理论中存在了很久。他们最初是由Richard Goodwin在1965或1967年应用过。
Physical meaning of the equations 方程的物理意义
The Lotka–Volterra model makes a number of assumptions, not necessarily realizable in nature, about the environment and evolution of the predator and prey populations:[21]
The Lotka–Volterra model makes a number of assumptions, not necessarily realizable in nature, about the environment and evolution of the predator and prey populations:
Lotka–Volterra模型对捕猎双方的环境和进化做出了许多假设,这些假设在自然界过于理想而不一定能实现:
- The prey population finds ample food at all times.
- The food supply of the predator population depends entirely on the size of the prey population.
- The rate of change of population is proportional to its size.
- During the process, the environment does not change in favour of one species, and genetic adaptation is inconsequential.
- Predators have limitless appetite.
- 猎物随时都有充足的食物。
- 捕食者种群的食物供应完全取决于猎物种群的大小。
- 各种群数量变化率与其规模成正比。
- 在此过程中,环境不会因一种物种而改变,并且无关于遗传适应性。
- 食肉动物有无限的食欲。
In this case the solution of the differential equations is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.[22]
In this case the solution of the differential equations is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.
在这种情况下,微分方程的解是确定并连续的。反过来,这也意味着掠食者和猎物的世代不断重叠。
Prey 猎物
When multiplied out, the prey equation becomes
When multiplied out, the prey equation becomes
当猎物数量成倍增趋势时,猎物方程变为:
- [math]\displaystyle{ \frac{dx}{dt} = \alpha x - \beta x y. }[/math]
The prey are assumed to have an unlimited food supply and to reproduce exponentially, unless subject to predation; this exponential growth is represented in the equation above by the term αx. The rate of predation upon the prey is assumed to be proportional to the rate at which the predators and the prey meet, this is represented above by βxy. If either x or y is zero, then there can be no predation.
The prey are assumed to have an unlimited food supply and to reproduce exponentially, unless subject to predation; this exponential growth is represented in the equation above by the term αx. The rate of predation upon the prey is assumed to be proportional to the rate at which the predators and the prey meet, this is represented above by βxy. If either or is zero, then there can be no predation.
假定猎物具有无限的食物供应,除非受到捕食,否则可以成倍繁殖,那么其指数增长由上式中的αx来表示。假设掠食者的掠食率,与掠食者和猎物的相遇率成正比,则用上式中的βxy表示。注意如果x或y为零,则表示没有掠夺。
With these two terms the equation above can be interpreted as follows: the rate of change of the prey's population is given by its own growth rate minus the rate at which it is preyed upon.
With these two terms the equation above can be interpreted as follows: the rate of change of the prey's population is given by its own growth rate minus the rate at which it is preyed upon.
基于该两个术语,上面的等式可以解释为:猎物种群的变化率由其自身数量的增长率减去被捕食数量的增长率得出。
Predators 捕食者
The predator equation becomes
The predator equation becomes
捕食者方程可以表示为:
- [math]\displaystyle{ \frac{dy}{dt} = \delta xy - \gamma y. }[/math]
In this equation, δxy represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used, as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). The term γy represents the loss rate of the predators due to either natural death or emigration, it leads to an exponential decay in the absence of prey.
In this equation, represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used, as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). The term represents the loss rate of the predators due to either natural death or emigration, it leads to an exponential decay in the absence of prey.
在此等式中,δxy代表捕食者种群的增长。(请注意此处与捕食率表达式虽然相似;但是使用了一个不同的常数,因为捕食者的生长速度不一定等于其消耗猎物的速度)。另外γy表示由于自然死亡或迁徙造成的捕食者数量减少率,它在没有猎物的情况下是指数衰减的。
Hence the equation expresses that the rate of change of the predator's population depends upon the rate at which it consumes prey, minus its intrinsic death rate.
Hence the equation expresses that the rate of change of the predator's population depends upon the rate at which it consumes prey, minus its intrinsic death rate.
因此,该等式表示,捕食者种群的变化率取决于其捕杀猎物的速率减去其固有死亡(包括迁徙)率。
Solutions to the equations 方程求解
The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions, although they are quite tractable.[23][24]
The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions, although they are quite tractable.
这些方程式具有周期解,但通常对于三角函数而言,虽然很容易处理,却并没有简单的表达式。
If none of the non-negative parameters α, β, γ, δ vanishes, three can be absorbed into the normalization of variables to leave only one parameter: since the first equation is homogeneous in x, and the second one in y, the parameters β/α and δ/γ are absorbable in the normalizations of y and x respectively, and γ into the normalization of t, so that only α/γ remains arbitrary. It is the only parameter affecting the nature of the solutions.
If none of the non-negative parameters vanishes, three can be absorbed into the normalization of variables to leave only one parameter: since the first equation is homogeneous in , and the second one in , the parameters β/α and δ/γ are absorbable in the normalizations of and respectively, and into the normalization of , so that only remains arbitrary. It is the only parameter affecting the nature of the solutions.
如果该方程组中所有非负参数α, β, γ, δ均存在,则可以将其中三个变量进行归一化,仅留下一个参数:由于第一个方程在x中是齐次的,而第二个方程在y中是齐次的,因此参数β/α 和 δ/γ分别在y和x中可以进行归一化处理,γ变成t的归一化,因此只有α/γ保持任意。并且它是影响解决方案性质的唯一参数。
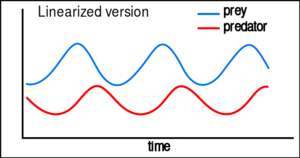
A linearization of the equations yields a solution similar to simple harmonic motion[25] with the population of predators trailing that of prey by 90° in the cycle.
A linearization of the equations yields a solution similar to simple harmonic motion with the population of predators trailing that of prey by 90° in the cycle.
方程的线性化类似于简谐运动的解,在周期中捕食者的数量比猎物的数量落后90°。
A simple example 简单示例
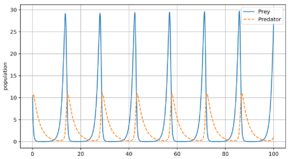
Suppose there are two species of animals, a baboon (prey) and a cheetah (predator). If the initial conditions are 10 baboons and 10 cheetahs, one can plot the progression of the two species over time; given the parameters that the growth and death rates of baboon are 1.1 and 0.4 while that of cheetahs are 0.1 and 0.4 respectively. The choice of time interval is arbitrary.
Suppose there are two species of animals, a baboon (prey) and a cheetah (predator). If the initial conditions are 10 baboons and 10 cheetahs, one can plot the progression of the two species over time; given the parameters that the growth and death rates of baboon are 1.1 and 0.4 while that of cheetahs are 0.1 and 0.4 respectively. The choice of time interval is arbitrary.
假设有两种动物,即狒狒(猎物)和猎豹(捕食者)。如果初始条件是10只狒狒和10只猎豹,则可以绘制出这两个物种随时间推移的数量。假设给定参数,狒狒的增长率和死亡率分别为1.1和0.4,而猎豹的增长率和死亡率分别为0.1和0.4,且时间间隔任意。
One may also plot solutions parametrically as orbits in phase space, without representing time, but with one axis representing the number of prey and the other axis representing the number of predators for all times.
One may also plot solutions parametrically as orbits in phase space, without representing time, but with one axis representing the number of prey and the other axis representing the number of predators for all times.
或者也可以在相空间轨道中将其解进行参数化处理,此时就可以略去时间轴。仅用其中一个轴代表全时间段猎物的数量,而另一轴代表全时间段掠食者的数量。
This corresponds to eliminating time from the two differential equations above to produce a single differential equation
This corresponds to eliminating time from the two differential equations above to produce a single differential equation
对应于上面的两个微分方程,此方法可以得出约掉时间参数的一个全新微分方程
- [math]\displaystyle{ \frac{dy}{dx} = - \frac{y}{x} \frac{\delta x - \gamma}{\beta y -\alpha} }[/math]
relating the variables x and y. The solutions of this equation are closed curves. It is amenable to separation of variables: integrating
relating the variables x and y. The solutions of this equation are closed curves. It is amenable to separation of variables: integrating
仅包含关联变量x 和 y。该方程的解是个闭合曲线,可以分离变量:对以下式子进行积分
- [math]\displaystyle{ \frac{\beta y - \alpha}{y} \,dy + \frac{\delta x - \gamma}{x} \,dx = 0 }[/math]
yields the implicit relationship
yields the implicit relationship
得到其隐性关系
- [math]\displaystyle{ V = \delta x - \gamma \ln(x) + \beta y - \alpha \ln(y), }[/math]
where V is a constant quantity depending on the initial conditions and conserved on each curve.
where V is a constant quantity depending on the initial conditions and conserved on each curve.
其中V是取决于初始条件的定量,并且在每条曲线上均守恒。
An aside: These graphs illustrate a serious potential problem with this as a biological model: For this specific choice of parameters, in each cycle, the baboon population is reduced to extremely low numbers, yet recovers (while the cheetah population remains sizeable at the lowest baboon density). In real-life situations, however, chance fluctuations of the discrete numbers of individuals, as well as the family structure and life-cycle of baboons, might cause the baboons to actually go extinct, and, by consequence, the cheetahs as well. This modelling problem has been called the "atto-fox problem", an atto-fox being a notional 10−18 of a fox.[26][27]
An aside: These graphs illustrate a serious potential problem with this as a biological model: For this specific choice of parameters, in each cycle, the baboon population is reduced to extremely low numbers, yet recovers (while the cheetah population remains sizeable at the lowest baboon density). In real-life situations, however, chance fluctuations of the discrete numbers of individuals, as well as the family structure and life-cycle of baboons, might cause the baboons to actually go extinct, and, by consequence, the cheetahs as well. This modelling problem has been called the "atto-fox problem", an atto-fox being a notional 10−18 of a fox.
另外值得注意的是,这些图说明了作为生物学模型的严重潜在问题:因为这种特定的参数选择,在每个周期中,狒狒的数量都被减少到极低的数量,但又有能力恢复(事实上,在极低的狒狒密度下,猎豹的数量仍然很大)。这显然在现实中是不太可能的,离散个体的偶然性波动,以及狒狒的家庭结构和生命周期都有可能导致狒狒种族灭绝,结果也就造成了猎豹的灭绝。按照此类方法建模出现的问题被称为“atto-fox问题”,“atto“这里指的是fox的十之负十八次方。
Phase-space plot of a further example 相空间图的进一步示例
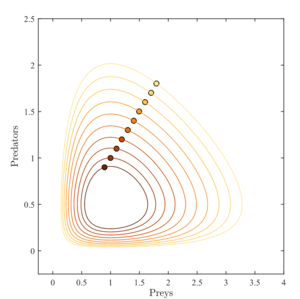
A less extreme example covers: α = 2/3, β = 4/3, γ = 1 = δ. Assume x, y quantify thousands each. Circles represent prey and predator initial conditions from x = y = 0.9 to 1.8, in steps of 0.1. The fixed point is at (1, 1/2).
A less extreme example covers: α = 2/3, β = 4/3, γ = 1 = δ. Assume x, y quantify thousands each. Circles represent prey and predator initial conditions from x = y = 0.9 to 1.8, in steps of 0.1. The fixed point is at (1, 1/2).
一个不太极端的示例包括: α = 2/3, β = 4/3, γ = 1 = δ. 假设x, y处于“千”级别还不到“万“。圆圈代表从x = y = 0.9 到 1.8时猎物和捕食者的初始条件,步长为0.1,且固定点在(1,1/2)。
Dynamics of the system 系统动力学
In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a cycle of growth and decline.
In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a cycle of growth and decline.
在该模型系统中,捕食者在有大量猎物的情况下肆意成长,但最终它们会因为食物供应不足而下降。随即捕食者数量变低,猎物数量将再次增加。就此形成的动力结构以增长和下降的周期持续。
Population equilibrium
Population equilibrium occurs in the model when neither of the population levels is changing, i.e. when both of the derivatives are equal to 0:
Population equilibrium occurs in the model when neither of the population levels is changing, i.e. when both of the derivatives are equal to 0:
人口均衡发生在模型中,当两个人口水平都没有变化时,即。当两个导数都等于0时:
- [math]\displaystyle{ x(\alpha - \beta y) = 0, }[/math]
[math]\displaystyle{ x(\alpha - \beta y) = 0, }[/math]
X (alpha-beta y) = 0
- [math]\displaystyle{ -y(\gamma - \delta x) = 0. }[/math]
[math]\displaystyle{ -y(\gamma - \delta x) = 0. }[/math]
< math >-y (gamma-delta x) = 0 </math >
The above system of equations yields two solutions:
The above system of equations yields two solutions:
上述方程组得出两个解:
- [math]\displaystyle{ \{y = 0,\ \ x = 0\} }[/math]
[math]\displaystyle{ \{y = 0,\ \ x = 0\} }[/math]
{ y = 0,x = 0}
and
and
及
- [math]\displaystyle{ \left\{y = \frac{\alpha}{\beta},\ \ x = \frac{\gamma}{\delta} \right\}. }[/math]
[math]\displaystyle{ \left\{y = \frac{\alpha}{\beta},\ \ x = \frac{\gamma}{\delta} \right\}. }[/math]
左{ y = frac { alpha }{ beta } ,x = frac { gamma }{ delta }右}
Hence, there are two equilibria.
Hence, there are two equilibria.
因此,有两个均衡。
The first solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zero numbers, and, in the simplified model, do so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters α, β, γ, and δ.
The first solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zero numbers, and, in the simplified model, do so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters α, β, γ, and δ.
第一个解决方案有效地代表了这两个物种的灭绝。如果两个种群都是0,那么它们将无限期地保持这种状态。第二个解表示一个固定点,在这个点上,两个种群都维持它们当前的非零数,并且在简化模型中,无限期地维持这个数。达到这种平衡的总体水平取决于参数 α,β,γ 和 δ 的选择值。
Stability of the fixed points
The stability of the fixed point at the origin can be determined by performing a linearization using partial derivatives.
The stability of the fixed point at the origin can be determined by performing a linearization using partial derivatives.
原点不动点的稳定性可以通过用偏导数进行线性化来确定。
The Jacobian matrix of the predator–prey model is
The Jacobian matrix of the predator–prey model is
该模型的雅可比矩阵为
- [math]\displaystyle{ J(x, y) = \begin{bmatrix} \lt math\gt J(x, y) = \begin{bmatrix} \lt math \gt j (x,y) = begin { bmatrix } \alpha - \beta y & -\beta x \\ \alpha - \beta y & -\beta x \\ Alpha-beta y &-beta x \delta y & \delta x - \gamma \delta y & \delta x - \gamma Delta y & delta x-gamma \end{bmatrix}. }[/math]
\end{bmatrix}.</math>
结束{ bmatrix } . </math >
and is known as the community matrix.
and is known as the community matrix.
被称为社区矩阵。
First fixed point (extinction)
When evaluated at the steady state of (0, 0), the Jacobian matrix J becomes
When evaluated at the steady state of (0, 0), the Jacobian matrix J becomes
当求解稳态(0,0)时,雅可比矩阵 j 变为
- [math]\displaystyle{ J(0, 0) = \begin{bmatrix} \lt math\gt J(0, 0) = \begin{bmatrix} (0,0) = begin { bmatrix } \alpha & 0 \\ \alpha & 0 \\ 阿尔法 & 0 0 & -\gamma 0 & -\gamma 0 &-gamma \end{bmatrix}. }[/math]
\end{bmatrix}.</math>
结束{ bmatrix } . </math >
The eigenvalues of this matrix are
The eigenvalues of this matrix are
这个矩阵的特征值是
- [math]\displaystyle{ \lambda_1 = \alpha, \quad \lambda_2 = -\gamma. }[/math]
[math]\displaystyle{ \lambda_1 = \alpha, \quad \lambda_2 = -\gamma. }[/math]
1 = alpha,quad lambda 2 =-gamma
In the model α and γ are always greater than zero, and as such the sign of the eigenvalues above will always differ. Hence the fixed point at the origin is a saddle point.
In the model α and γ are always greater than zero, and as such the sign of the eigenvalues above will always differ. Hence the fixed point at the origin is a saddle point.
在模型中,α 和 γ 总是大于零,因此上述特征值的符号总是不同的。因此原点的不动点是鞍点。
The stability of this fixed point is of significance. If it were stable, non-zero populations might be attracted towards it, and as such the dynamics of the system might lead towards the extinction of both species for many cases of initial population levels. However, as the fixed point at the origin is a saddle point, and hence unstable, it follows that the extinction of both species is difficult in the model. (In fact, this could only occur if the prey were artificially completely eradicated, causing the predators to die of starvation. If the predators were eradicated, the prey population would grow without bound in this simple model.) The populations of prey and predator can get infinitesimally close to zero and still recover.
The stability of this fixed point is of significance. If it were stable, non-zero populations might be attracted towards it, and as such the dynamics of the system might lead towards the extinction of both species for many cases of initial population levels. However, as the fixed point at the origin is a saddle point, and hence unstable, it follows that the extinction of both species is difficult in the model. (In fact, this could only occur if the prey were artificially completely eradicated, causing the predators to die of starvation. If the predators were eradicated, the prey population would grow without bound in this simple model.) The populations of prey and predator can get infinitesimally close to zero and still recover.
这个不动点的稳定性具有重要意义。如果它是稳定的,可能会吸引非零种群,因此,在许多初始种群水平的情况下,系统的动态可能导致两个物种的灭绝。然而,由于原点的不动点是鞍点,因此是不稳定的,因此在模型中两种物种的灭绝都是困难的。(事实上,只有当猎物被人为地完全消灭,导致捕食者饿死时,才会发生这种情况。如果捕食者被消灭,在这个简单的模型中,被捕食者的数量将会无限增长捕食者和被捕食者的数量可以无限小地接近于零,并且仍然可以恢复。
Second fixed point (oscillations)
Evaluating J at the second fixed point leads to
Evaluating J at the second fixed point leads to
在第二个固定点上对 j 进行评价
- [math]\displaystyle{ J\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) = \begin{bmatrix} \lt math\gt J\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) = \begin{bmatrix} J left (frac { gamma }{ delta } ,frac { alpha }{ beta }右) = begin { bmatrix } 0 & -\frac{\beta \gamma}{\delta} \\ 0 & -\frac{\beta \gamma}{\delta} \\ 0 &-frac { beta gamma }{ delta } \frac{\alpha \delta}{\beta} & 0 \frac{\alpha \delta}{\beta} & 0 0.0.0 \end{bmatrix}. }[/math]
\end{bmatrix}.</math>
结束{ bmatrix } . </math >
The eigenvalues of this matrix are
The eigenvalues of this matrix are
这个矩阵的特征值是
- [math]\displaystyle{ \lambda_1 = i \sqrt{\alpha \gamma}, \quad \lambda_2 = -i \sqrt{\alpha \gamma}. \lt math\gt \lambda_1 = i \sqrt{\alpha \gamma}, \quad \lambda_2 = -i \sqrt{\alpha \gamma}. 1 = i sqrt { alpha gamma } ,quad lambda 2 =-i sqrt { alpha gamma }. }[/math]
</math>
数学
As the eigenvalues are both purely imaginary and conjugate to each others, this fixed point is elliptic, so the solutions are periodic, oscillating on a small ellipse around the fixed point, with a frequency [math]\displaystyle{ \omega = \sqrt{\lambda_1 \lambda_2} = \sqrt{\alpha \gamma} }[/math] and period [math]\displaystyle{ T = 2{\pi}/(\sqrt{\lambda_1 \lambda_2}) }[/math].
As the eigenvalues are both purely imaginary and conjugate to each others, this fixed point is elliptic, so the solutions are periodic, oscillating on a small ellipse around the fixed point, with a frequency [math]\displaystyle{ \omega = \sqrt{\lambda_1 \lambda_2} = \sqrt{\alpha \gamma} }[/math] and period [math]\displaystyle{ T = 2{\pi}/(\sqrt{\lambda_1 \lambda_2}) }[/math].
由于本征值都是纯虚的,并且彼此共轭,这个不动点是椭圆的,所以解是周期性的,振荡在一个小椭圆上围绕着不动点,具有频率 < math > omega = sqrt { αγ } </math > 和周期 < math > t = 2{ pi }/(sqrt { lambda _ 1 da _ 2}) </math > 。
As illustrated in the circulating oscillations in the figure above, the level curves are closed orbits surrounding the fixed point: the levels of the predator and prey populations cycle and oscillate without damping around the fixed point with frequency [math]\displaystyle{ \omega = \sqrt{\alpha \gamma} }[/math].
As illustrated in the circulating oscillations in the figure above, the level curves are closed orbits surrounding the fixed point: the levels of the predator and prey populations cycle and oscillate without damping around the fixed point with frequency [math]\displaystyle{ \omega = \sqrt{\alpha \gamma} }[/math].
如上图所示,水平曲线是围绕固定点的闭合轨道: 捕食者和被捕食者种群的水平循环,在固定点周围振荡而没有阻尼,频率 < math > omega = sqrt { alpha } </math > 。
The value of the constant of motion V, or, equivalently, K = exp(V), [math]\displaystyle{ K = y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} }[/math], can be found for the closed orbits near the fixed point.
The value of the constant of motion V, or, equivalently, K = exp(V), [math]\displaystyle{ K = y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} }[/math], can be found for the closed orbits near the fixed point.
运动常数 v 的值,或者等价地 k = exp (v) ,< math > k = y ^ αe ^ {-beta y } x ^ gamma ^ {-delta x } </math > ,可以在不动点附近的闭合轨道上找到。
Increasing K moves a closed orbit closer to the fixed point. The largest value of the constant K is obtained by solving the optimization problem
Increasing K moves a closed orbit closer to the fixed point. The largest value of the constant K is obtained by solving the optimization problem
增 k 使闭合轨道更接近于固定点。常数 k 的最大值是通过求解最佳化问题得到的
- [math]\displaystyle{ y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} = \frac{y^\alpha x^\gamma}{e^{\delta x+\beta y}} \longrightarrow \max\limits_{x,y\gt 0}. }[/math]
[math]\displaystyle{ y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} = \frac{y^\alpha x^\gamma}{e^{\delta x+\beta y}} \longrightarrow \max\limits_{x,y\gt 0}. }[/math]
< math > y ^ alpha ^ e ^ {-beta y } x ^ gamma ^ {-delta x } = frac { y ^ alpha ^ gamma }{ e ^ { delta x + beta y }}{ longright tarrow max limits { x,y > 0}。 </math >
The maximal value of K is thus attained at the stationary (fixed) point [math]\displaystyle{ \left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) }[/math] and amounts to
The maximal value of K is thus attained at the stationary (fixed) point [math]\displaystyle{ \left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) }[/math] and amounts to
因此,k 的最大值是在稳定(不动)点 < math > 左(frac { gamma }{ delta } ,frac { alpha }{ beta }右) </math >
- [math]\displaystyle{ K^* = \left(\frac{\alpha}{\beta e}\right)^\alpha \left(\frac{\gamma}{\delta e}\right)^\gamma, }[/math]
[math]\displaystyle{ K^* = \left(\frac{\alpha}{\beta e}\right)^\alpha \left(\frac{\gamma}{\delta e}\right)^\gamma, }[/math]
< math > k ^ * = left (frac { alpha }{ beta e } right) ^ alpha left (frac { gamma }{ delta e } right) ^ gamma,</math >
where e is Euler's number.
where e is Euler's number.
其中 e 是欧拉数。
See also
- Lanchester's laws, a similar system of differential equations for military forces
Notes
- ↑ Freedman, H. I. (1980). Deterministic Mathematical Models in Population Ecology. Marcel Dekker.
- ↑ Brauer, F.; Castillo-Chavez, C. (2000). Mathematical Models in Population Biology and Epidemiology. Springer-Verlag.
- ↑ Hoppensteadt, F. (2006). "Predator-prey model". Scholarpedia. 1 (10): 1563. Bibcode:2006SchpJ...1.1563H. doi:10.4249/scholarpedia.1563.
- ↑ Lotka, A. J. (1910). "Contribution to the Theory of Periodic Reaction". J. Phys. Chem. 14 (3): 271–274. doi:10.1021/j150111a004.
- ↑ 5.0 5.1 Goel, N. S. (1971). On the Volterra and Other Non-Linear Models of Interacting Populations. Academic Press.
- ↑ Berryman, A. A. (1992). "The Origins and Evolution of Predator-Prey Theory" (PDF). Ecology. 73 (5): 1530–1535. doi:10.2307/1940005. JSTOR 1940005. Archived from the original (PDF) on 2010-05-31.
- ↑ Verhulst, P. H. (1838). "Notice sur la loi que la population poursuit dans son accroissement". Corresp. Mathématique et Physique. 10: 113–121.
- ↑ Lotka, A. J. (1920). "Analytical Note on Certain Rhythmic Relations in Organic Systems". Proc. Natl. Acad. Sci. U.S.A. 6 (7): 410–415. Bibcode:1920PNAS....6..410L. doi:10.1073/pnas.6.7.410. PMC 1084562. PMID 16576509.
- ↑ Lotka, A. J. (1925). Elements of Physical Biology. Williams and Wilkins.
- ↑ Volterra, V. (1926). "Variazioni e fluttuazioni del numero d'individui in specie animali conviventi". Mem. Acad. Lincei Roma. 2: 31–113.
- ↑ Volterra, V. (1931). "Variations and fluctuations of the number of individuals in animal species living together". In Chapman, R. N.. Animal Ecology. McGraw–Hill.
- ↑ Kingsland, S. (1995). Modeling Nature: Episodes in the History of Population Ecology. University of Chicago Press. ISBN 978-0-226-43728-6.
- ↑ Rosenzweig, M. L.; MacArthur, R.H. (1963). "Graphical representation and stability conditions of predator-prey interactions". American Naturalist. 97 (895): 209–223. doi:10.1086/282272. S2CID 84883526.
- ↑ Gilpin, M. E. (1973). "Do hares eat lynx?". American Naturalist. 107 (957): 727–730. doi:10.1086/282870. S2CID 84794121.
- ↑ Jost, C.; Devulder, G.; Vucetich, J.A.; Peterson, R.; Arditi, R. (2005). "The wolves of Isle Royale display scale-invariant satiation and density dependent predation on moose". J. Anim. Ecol. 74 (5): 809–816. doi:10.1111/j.1365-2656.2005.00977.x.
- ↑ Arditi, R.; Ginzburg, L. R. (1989). "Coupling in predator-prey dynamics: ratio dependence" (PDF). Journal of Theoretical Biology. 139 (3): 311–326. doi:10.1016/s0022-5193(89)80211-5.
- ↑ Abrams, P. A.; Ginzburg, L. R. (2000). "The nature of predation: prey dependent, ratio dependent or neither?". Trends in Ecology & Evolution. 15 (8): 337–341. doi:10.1016/s0169-5347(00)01908-x. PMID 10884706.
- ↑ Gandolfo, G. (2008). "Giuseppe Palomba and the Lotka–Volterra equations". Rendiconti Lincei. 19 (4): 347–357. doi:10.1007/s12210-008-0023-7. S2CID 140537163.
- ↑ Goodwin, R. M. (1967). "A Growth Cycle". In Feinstein, C. H.. Socialism, Capitalism and Economic Growth. Cambridge University Press. https://archive.org/details/socialismcapital0000fein.
- ↑ Desai, M.; Ormerod, P. (1998). "Richard Goodwin: A Short Appreciation" (PDF). The Economic Journal. 108 (450): 1431–1435. CiteSeerX 10.1.1.423.1705. doi:10.1111/1468-0297.00350. Archived from the original (PDF) on 2011-09-27. Retrieved 2010-03-22.
- ↑ "PREDATOR-PREY DYNAMICS". www.tiem.utk.edu. Retrieved 2018-01-09.
- ↑ Cooke, D.表达式错误:无法识别的词语“etal”。 (1981). The Mathematical Theory of the Dynamics of Biological Populations. II. Academic Press.
- ↑ Steiner, Antonio; Gander, Martin Jakob (1999). "Parametrische Lösungen der Räuber-Beute-Gleichungen im Vergleich". Il Volterriano. 7: 32–44.
- ↑ Evans, C. M.; Findley, G. L. (1999). "A new transformation for the Lotka-Volterra problem". Journal of Mathematical Chemistry. 25: 105–110. doi:10.1023/A:1019172114300. S2CID 36980176.
- ↑ Tong, H. (1983). Threshold Models in Non-linear Time Series Analysis. Springer–Verlag.
- ↑ Lobry, Claude; Sari, Tewfik (2015). "Migrations in the Rosenzweig-MacArthur model and the "atto-fox" problem" (PDF). Arima. 20: 95–125.
- ↑ Mollison, D. (1991). "Dependence of epidemic and population velocities on basic parameters" (PDF). Math. Biosci. 107 (2): 255–287. doi:10.1016/0025-5564(91)90009-8. PMID 1806118.
References
- Leigh, E. R. (1968). "The ecological role of Volterra's equations". Some Mathematical Problems in Biology. – a modern discussion using Hudson's Bay Company data on lynx and hares in Canada from 1847 to 1903.
- Kaplan, Daniel; Glass, Leon (1995). Understanding Nonlinear Dynamics. New York: Springer. ISBN 978-0-387-94440-1. https://archive.org/details/understandingnon0000kapl.
- Murray, J. D. (2003). Mathematical Biology I: An Introduction. New York: Springer. ISBN 978-0-387-95223-9.
- Yorke, James A.; Anderson, William N. Jr. (1973). "Predator-Prey Patterns (Volterra-Lotka equations)" (PDF). PNAS. 70 (7): 2069–2071. doi:10.1073/pnas.70.7.2069. JSTOR 62597. PMC 433667. PMID 16592100.
- Llibre, J.; Valls, C. (2007). "Global analytic first integrals for the real planar Lotka-Volterra system". J. Math. Phys. 48 (3): 033507. Bibcode:2007JMP....48c3507L. doi:10.1063/1.2713076.
External links
- From the Wolfram Demonstrations Project — requires CDF player (free):
- Lotka-Volterra Algorithmic Simulation (Web simulation).
Category:Predation
类别: 掠夺
Category:Ordinary differential equations
类别: 常微分方程
Category:Fixed points (mathematics)
类别: 定点(数学)
Category:Population models
类别: 人口模型
Category:Mathematical modeling
类别: 数学建模
Category:Community ecology
类别: 群落交错区
This page was moved from wikipedia:en:Lotka–Volterra equations. Its edit history can be viewed at Lotka–Volterra方程式/edithistory