“Do演算”的版本间的差异
(→应用案例1) |
(更新框架) |
||
| 第9行: | 第9行: | ||
而Do演算是一个具有完备性的推演系统,可以处理所有可识别的模型,当然也就包括了右侧图中这个例子。同时,利用Do演算还有一系列的计算机算法,可以自动、高速地去判断一个模型的可识别性,并在可识别的模型中将包含Do算子的概率分布表达式转换为仅包含观测变量的概率分布表达式。 | 而Do演算是一个具有完备性的推演系统,可以处理所有可识别的模型,当然也就包括了右侧图中这个例子。同时,利用Do演算还有一系列的计算机算法,可以自动、高速地去判断一个模型的可识别性,并在可识别的模型中将包含Do算子的概率分布表达式转换为仅包含观测变量的概率分布表达式。 | ||
| − | === | + | === Do演算规则集 === |
在以下规则的表述中,使用符号<math>G_{\overline{X}}</math>表示删除有向图<math>G</math>中所有指向结点<math>X</math>的边后得到的子图,使用符号<math>G_{\overline{X}\underline{Z}}</math>表示删除有向图<math>G</math>中所有指向结点<math>X</math>的边和从结点<math>Z</math>指出的边后得到的子图。 | 在以下规则的表述中,使用符号<math>G_{\overline{X}}</math>表示删除有向图<math>G</math>中所有指向结点<math>X</math>的边后得到的子图,使用符号<math>G_{\overline{X}\underline{Z}}</math>表示删除有向图<math>G</math>中所有指向结点<math>X</math>的边和从结点<math>Z</math>指出的边后得到的子图。 | ||
| 第40行: | 第40行: | ||
要证明上述定理的正确性,需要分别证明Do演算的可靠性(Soundness)和充分性(Sufficiency)。其中可靠性的证明由Judea Pearl于1995年给出<ref name="pearl:95">{{citation | last = Pearl | first = Judea | doi = 10.1093/biomet/82.4.669 | issue = 4 | journal = Biometrika | pages = 669–710 | title = Causal diagrams for empirical research | volume = 82 | year = 1995| url = https://escholarship.org/uc/item/6gv9n38c }}.</ref>,充分性的证明由Yimin Huang和Marco Valtorta于2006年给出<ref name="huang:06">{{cite journal |last1=Huang |first1=Yimin |last2=Valtorta |first2=Marco |date=2006 |title=Pearl's Calculus of Intervention is Complete |url= |journal=Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence |pages=217–224}}</ref>。 | 要证明上述定理的正确性,需要分别证明Do演算的可靠性(Soundness)和充分性(Sufficiency)。其中可靠性的证明由Judea Pearl于1995年给出<ref name="pearl:95">{{citation | last = Pearl | first = Judea | doi = 10.1093/biomet/82.4.669 | issue = 4 | journal = Biometrika | pages = 669–710 | title = Causal diagrams for empirical research | volume = 82 | year = 1995| url = https://escholarship.org/uc/item/6gv9n38c }}.</ref>,充分性的证明由Yimin Huang和Marco Valtorta于2006年给出<ref name="huang:06">{{cite journal |last1=Huang |first1=Yimin |last2=Valtorta |first2=Marco |date=2006 |title=Pearl's Calculus of Intervention is Complete |url= |journal=Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence |pages=217–224}}</ref>。 | ||
| − | === | + | === 应用案例 === |
==== 应用案例1 ==== | ==== 应用案例1 ==== | ||
| 第54行: | 第54行: | ||
* 第七步:(使用规则三)<math>\Sigma_{s'}\Sigma_t P(c \mid t,s')P(s' \mid do(t))P(t \mid s) = \Sigma_{s'}\Sigma_t P(c \mid t,s')P(s')P(t \mid s)</math> | * 第七步:(使用规则三)<math>\Sigma_{s'}\Sigma_t P(c \mid t,s')P(s' \mid do(t))P(t \mid s) = \Sigma_{s'}\Sigma_t P(c \mid t,s')P(s')P(t \mid s)</math> | ||
| − | === | + | === 相关算法 === |
==== 算法一 ==== | ==== 算法一 ==== | ||
算法1 | 算法1 | ||
| + | |||
| + | === 代码实现 === | ||
| + | |||
| + | 软件/代码信息 | ||
2021年7月18日 (日) 20:14的版本
Do演算(Do-Calculus)是由三条推演规则构成的推演系统,这三条规则可以将包含干预变量和观测变量的概率分布表达式进行转化。
为何需要Do演算
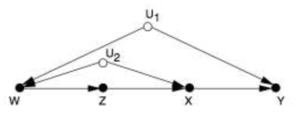
在处理一部分因果图时,可以使用后门调整和前门调整等技术进行统计调整,这样可以根据不涉及Do算子的数据来估算干预的效果。然而我们无法根据前门准则和后门准则事先确定一个给定的因果模型是否适用于这样的统计调整方式。后门调整和前门调整方法也无法处理所有可识别的模型,例如右侧的因果图是可识别的,但既无法使用后门调整也无法使用前门调整。
而Do演算是一个具有完备性的推演系统,可以处理所有可识别的模型,当然也就包括了右侧图中这个例子。同时,利用Do演算还有一系列的计算机算法,可以自动、高速地去判断一个模型的可识别性,并在可识别的模型中将包含Do算子的概率分布表达式转换为仅包含观测变量的概率分布表达式。
Do演算规则集
在以下规则的表述中,使用符号[math]\displaystyle{ G_{\overline{X}} }[/math]表示删除有向图[math]\displaystyle{ G }[/math]中所有指向结点[math]\displaystyle{ X }[/math]的边后得到的子图,使用符号[math]\displaystyle{ G_{\overline{X}\underline{Z}} }[/math]表示删除有向图[math]\displaystyle{ G }[/math]中所有指向结点[math]\displaystyle{ X }[/math]的边和从结点[math]\displaystyle{ Z }[/math]指出的边后得到的子图。
规则一
增添或删除观察:
对于有向图[math]\displaystyle{ G }[/math],若满足[math]\displaystyle{ (Y \perp\!\!\!\perp Z \mid X, W)_{G_{\overline{X}}} }[/math](即在子图[math]\displaystyle{ G_{\overline{X}} }[/math]中,给定结点集[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math]时,结点集[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]满足d-分离条件),则
- [math]\displaystyle{ P(Y|do(X),Z,W)=P(Y|do(X),Z) }[/math]
规则二
交换干预和观察:
对于有向图[math]\displaystyle{ G }[/math],若满足[math]\displaystyle{ (Y \perp\!\!\!\perp Z \mid X, W)_{G_{\overline{X}\underline{Z}}} }[/math](即在子图[math]\displaystyle{ G_{\overline{X}\underline{Z}} }[/math]中,给定结点集[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math]时,结点集[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]满足d-分离条件),则
- [math]\displaystyle{ P(Y|do(X),do(Z),W)=P(Y|do(X),Z,W) }[/math]
规则三
增添或删除干预:
对于有向图[math]\displaystyle{ G }[/math],若满足[math]\displaystyle{ (Y \perp\!\!\!\perp Z \mid X, W)_{G_{\overline{X}\underline{Z(W)}}} }[/math](即在子图[math]\displaystyle{ G_{\overline{X}\underline{Z(W)}} }[/math]中,给定结点集[math]\displaystyle{ X }[/math]和[math]\displaystyle{ W }[/math]时,结点集[math]\displaystyle{ Y }[/math]和[math]\displaystyle{ Z }[/math]满足d-分离条件),则
- [math]\displaystyle{ P(Y|do(X),do(Z),W)=P(Y|do(X),W) }[/math]
其中符号[math]\displaystyle{ Z(W) }[/math] 表示 [math]\displaystyle{ Z / An(W)_{ G_{ \overline{X} } } }[/math] ,而符号[math]\displaystyle{ An(W)_{ G_{ \overline{X} } } }[/math] 表示在子图[math]\displaystyle{ G_{ \overline{X}} }[/math]中由结点集[math]\displaystyle{ W }[/math]及其祖先节点构成的点集。
Do演算的完备性(Completeness)
定理
[math]\displaystyle{ Q = P(y \mid do(x),z) }[/math] 是可识别的,当且仅当它可以被Do演算的三条规则转化为一个不包含Do算子的表达式。
证明
要证明上述定理的正确性,需要分别证明Do演算的可靠性(Soundness)和充分性(Sufficiency)。其中可靠性的证明由Judea Pearl于1995年给出[1],充分性的证明由Yimin Huang和Marco Valtorta于2006年给出[2]。
应用案例
应用案例1
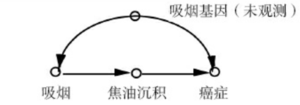
在右侧的因果图中,“吸烟基因”是未观测变量,其余变量都是可观测的。“吸烟”变量使用[math]\displaystyle{ s }[/math]来表示,“焦油沉积”变量使用[math]\displaystyle{ t }[/math]来表示,“癌症”变量使用[math]\displaystyle{ c }[/math]来表示。我们要估计干预“吸烟”变量后对“癌症”变量的因果效应,即计算[math]\displaystyle{ P(c \mid do(s)) }[/math]。我们将使用Do演算将这个表达式转换为不包含Do算子的表达式。
- 第一步:(使用概率公理)[math]\displaystyle{ P(c \mid do(s)) = \Sigma_t P(c \mid do(s), t)P(t \mid do(s)) }[/math]
- 第二步:(使用规则二)[math]\displaystyle{ \Sigma_t P(c \mid do(s), t)P(t \mid do(s)) = \Sigma_t P(c \mid do(s), do(t))P(t \mid do(s)) }[/math]
- 第三步:(使用规则二)[math]\displaystyle{ \Sigma_t P(c \mid do(s), do(t))P(t \mid do(s)) = \Sigma_t P(c \mid do(s), do(t))P(t \mid s) }[/math]
- 第四步:(使用规则三)[math]\displaystyle{ \Sigma_t P(c \mid do(s), do(t))P(t \mid s) = \Sigma_t P(c \mid do(t))P(t \mid s) }[/math]
- 第五步:(使用概率公理)[math]\displaystyle{ \Sigma_t P(c \mid do(t))P(t \mid s) = \Sigma_{s'}\Sigma_t P(c \mid do(t),s')P(s' \mid do(t))P(t \mid s) }[/math]
- 第六步:(使用规则二)[math]\displaystyle{ \Sigma_{s'}\Sigma_t P(c \mid do(t),s')P(s' \mid do(t))P(t \mid s) = \Sigma_{s'}\Sigma_t P(c \mid t,s')P(s' \mid do(t))P(t \mid s) }[/math]
- 第七步:(使用规则三)[math]\displaystyle{ \Sigma_{s'}\Sigma_t P(c \mid t,s')P(s' \mid do(t))P(t \mid s) = \Sigma_{s'}\Sigma_t P(c \mid t,s')P(s')P(t \mid s) }[/math]
相关算法
算法一
算法1
代码实现
软件/代码信息
- ↑ Pearl, Judea (1995), "Causal diagrams for empirical research", Biometrika, 82 (4): 669–710, doi:10.1093/biomet/82.4.669.
- ↑ Huang, Yimin; Valtorta, Marco (2006). "Pearl's Calculus of Intervention is Complete". Proceedings of the Twenty-Second Conference on Uncertainty in Artificial Intelligence: 217–224.