“网络可控性”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第10行： 第10行：
  
 
== 背景 ==
 
== 背景 ==
−
考虑'''复杂网络 Complex Network '''上的经典线性时不变动力学
+
考虑'''复杂网络 Complex Network'''上的经典线性时不变动力学
  
 
<math>
 
<math>
第18行： 第18行：
 
其中，向量 <math>\mathbf{X}(t)=(x_1(t),\cdots,x_N(t))^\mathrm{T}</math> 表示在 <math>N</math> 个节点的系统时间 <math>t</math>时的状态。
 
其中，向量 <math>\mathbf{X}(t)=(x_1(t),\cdots,x_N(t))^\mathrm{T}</math> 表示在 <math>N</math> 个节点的系统时间 <math>t</math>时的状态。
  
−
<math>N \times N</math> 的矩阵 <math>\mathbf{A}</math> 描述了系统的连接图以及各组分之间的交互强度。<math>N \times M</math> 矩阵 <math>\mathbf{B}</math> 列出了由外部控制器控制的节点。控制器通过施加给系统的时间相关向量 <math>\mathbf{u}(t) = (u_1(t),\cdots,u_M(t))^\mathrm{T}</math> 来实现对系统的控制。为了确定驱动节点的最小数目，<math>N_\mathrm{D}</math>，亦即确定对最少几个节点施加控制便足以完全控制系统的动力学进程，在这方面，Liu等人尝试了'''将结构控制理论 Structural Control Theory '''、'''图论 Graph Theory '''和'''统计物理 Statistical Physics '''的工具的结合。<ref name="Liu-Nature-11">{{cite journal | last=Liu | first=Yang-Yu | last2=Slotine | first2=Jean-Jacques | last3=Barabási | first3=Albert-László | title=Controllability of complex networks | journal=Nature | publisher=Springer Science and Business Media LLC | volume=473 | issue=7346 | year=2011 | issn=0028-0836 | doi=10.1038/nature10011 | pages=167–173}}</ref> 他们发现<ref name="Liu-Nature-11"/>，完全控制一个网络所需要的最少输入或驱动节点，取决于网络的'''最大匹配 maximum matching'''，也就是不共享起始顶点和终止顶点的最大边集。从这个结论出发，一个基于''入-出度分布''的分析框架被开发出来，用于预测'''无标度网络 scale-free network'''和'''ER随即图 Erdős–Rényi Graph<ref name="Liu-Nature-11"/> '''的<math>n_\mathrm{D} =N_\mathrm{D}/N </math>值。<ref name="gates_rocha_scirep">{{cite journal | last=Gates | first=Alexander J. | last2=Rocha | first2=Luis M. | title=Control of complex networks requires both structure and dynamics | journal=Scientific Reports | publisher=Springer Science and Business Media LLC | volume=6 | issue=1 | date=2016-04-18 | issn=2045-2322 | doi=10.1038/srep24456 | page=24456|doi-access=free}}</ref>
+
<math>N \times N</math> 的矩阵 <math>\mathbf{A}</math> 描述了系统的连接图以及各组分之间的交互强度。<math>N \times M</math> 矩阵 <math>\mathbf{B}</math> 列出了由外部控制器控制的节点。控制器通过施加给系统的时间相关向量 <math>\mathbf{u}(t) = (u_1(t),\cdots,u_M(t))^\mathrm{T}</math> 来实现对系统的控制。为了确定驱动节点的最小数目，<math>N_\mathrm{D}</math>，亦即确定对最少几个节点施加控制便足以完全控制系统的动力学进程，在这方面，Liu等人尝试了'''将结构控制理论 Structural Control Theory'''、'''图论 Graph Theory '''和'''统计物理 Statistical Physics'''的工具的结合。<ref name="Liu-Nature-11">{{cite journal | last=Liu | first=Yang-Yu | last2=Slotine | first2=Jean-Jacques | last3=Barabási | first3=Albert-László | title=Controllability of complex networks | journal=Nature | publisher=Springer Science and Business Media LLC | volume=473 | issue=7346 | year=2011 | issn=0028-0836 | doi=10.1038/nature10011 | pages=167–173}}</ref> 他们发现<ref name="Liu-Nature-11"/>，完全控制一个网络所需要的最少输入或驱动节点，取决于网络的'''最大匹配 maximum matching'''，也就是不共享起始顶点和终止顶点的最大边集。从这个结论出发，一个基于''入-出度分布''的分析框架被开发出来，用于预测'''无标度网络 scale-free network'''和'''ER随即图 Erdős–Rényi Graph<ref name="Liu-Nature-11"/>'''的<math>n_\mathrm{D} =N_\mathrm{D}/N </math>值。<ref name="gates_rocha_scirep">{{cite journal | last=Gates | first=Alexander J. | last2=Rocha | first2=Luis M. | title=Control of complex networks requires both structure and dynamics | journal=Scientific Reports | publisher=Springer Science and Business Media LLC | volume=6 | issue=1 | date=2016-04-18 | issn=2045-2322 | doi=10.1038/srep24456 | page=24456|doi-access=free}}</ref>
  
−
同样值得关注的是，刘等人的工作<ref name="Liu-Nature-11"/>提出了这么一个问题<ref name = "Arxiv_Close_Betw">{{cite arXiv|first=SJ |last=Banerjee |first2=S |last2=Roy|title=Key to Network Controllability|eprint=1209.3737}}</ref> ：'''度 Degree ''',作为网络中一种纯粹的局部度量，能否完全描述网络的可控性？是不是即便稍微远一点的节点，就对网络的可控性没有影响？事实上，对于许多'''现实世界里的网络 Real-World Networks '''，像'''食物网络 Food Webs '''、'''神经元网络 Neuronal Network ''' 和'''代谢网络 Metabolic Network '''，Liu等人计算的<math>{n_\mathrm{D}}^{real}</math><math>和{n_\mathrm{D}}^\mathrm{rand\_degree}</math> 的值并不匹配<ref name="Liu-Nature-11"/>。值得注意的是。如果可控性主要是由度决定，那么为什么对于许多现实世界的网络来说，<math>{n_\mathrm{D}}^{real}</math> 和 <math>{n_\mathrm{D}}^\mathrm{rand\_degree}</math> 如此不同？他们认为<ref name="Liu-Nature-11"/>，这可能是由于度相关性的影响。然而，已有的研究表明<ref name = "Arxiv_Close_Betw"/>，网络的可控性只能通过中间性和封闭性来改变，而完全不需要使用度（图论）或'''度相关性 Degree Correlations '''。(arXiv:1203.5161v1)
+
同样值得关注的是，刘等人的工作<ref name="Liu-Nature-11"/>提出了这么一个问题<ref name = "Arxiv_Close_Betw">{{cite arXiv|first=SJ |last=Banerjee |first2=S |last2=Roy|title=Key to Network Controllability|eprint=1209.3737}}</ref> ：'''度 Degree''',作为网络中一种纯粹的局部度量，能否完全描述网络的可控性？是不是即便稍微远一点的节点，就对网络的可控性没有影响？事实上，对于许多'''现实世界里的网络 Real-World Networks'''，像'''食物网络 Food Webs'''、'''神经元网络 Neuronal Network''' 和'''代谢网络 Metabolic Network'''，Liu等人计算的<math>{n_\mathrm{D}}^{real}</math><math>和{n_\mathrm{D}}^\mathrm{rand\_degree}</math> 的值并不匹配<ref name="Liu-Nature-11"/>。值得注意的是。如果可控性主要是由度决定，那么为什么对于许多现实世界的网络来说，<math>{n_\mathrm{D}}^{real}</math> 和 <math>{n_\mathrm{D}}^\mathrm{rand\_degree}</math> 如此不同？他们认为<ref name="Liu-Nature-11"/>，这可能是由于度相关性的影响。然而，已有的研究表明<ref name = "Arxiv_Close_Betw"/>，网络的可控性只能通过中间性和封闭性来改变，而完全不需要使用度（图论）或'''度相关性 Degree Correlations'''。(arXiv:1203.5161v1)
  
 
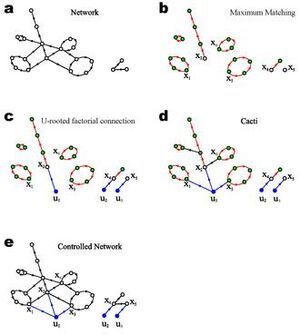
[[File:page1-330px-YYL2.pdf.jpg|right|thumb|示意图显示了一个有向向网络的控制。对于给定的有向网络（图a），可以计算其最大匹配：没有共同头部或尾部的最大边集。最大匹配将由一组顶点不相交的有向路径和有向环组成（请参见图b中的红色边缘）。如果一个节点是匹配边的头部，则该节点是匹配的（图b中的绿色节点）。否则，它是不匹配的（图b中的白色节点）。那些不匹配的节点是需要施加控制的节点，即驱动节点。通过向这些驱动节点注入信号，可以得到一组以起点为输入的有向路径（见图c）。这些路径被称为“茎”。得到的有向图称为U根因子连接。通过将定向周期“嫁接”到那些“茎”，人们就会得到“芽”。得到的有向图称为'''仙人掌 cacti'''（见图d）。根据结构可控性定理，由于存在跨越受控网络的cacti结构（参见图e），因此该系统是可控的。受控网络（图e）下的cacti结构（图d）是维持可控性的“骨架”。]]
 
[[File:page1-330px-YYL2.pdf.jpg|right|thumb|示意图显示了一个有向向网络的控制。对于给定的有向网络（图a），可以计算其最大匹配：没有共同头部或尾部的最大边集。最大匹配将由一组顶点不相交的有向路径和有向环组成（请参见图b中的红色边缘）。如果一个节点是匹配边的头部，则该节点是匹配的（图b中的绿色节点）。否则，它是不匹配的（图b中的白色节点）。那些不匹配的节点是需要施加控制的节点，即驱动节点。通过向这些驱动节点注入信号，可以得到一组以起点为输入的有向路径（见图c）。这些路径被称为“茎”。得到的有向图称为U根因子连接。通过将定向周期“嫁接”到那些“茎”，人们就会得到“芽”。得到的有向图称为'''仙人掌 cacti'''（见图d）。根据结构可控性定理，由于存在跨越受控网络的cacti结构（参见图e），因此该系统是可控的。受控网络（图e）下的cacti结构（图d）是维持可控性的“骨架”。]]
第29行： 第29行：
  
 
=== 最大匹配 ===
 
=== 最大匹配 ===
−
在图论中，匹配（图论）是一组没有共同顶点的边。Liu等人<ref name="Liu-Nature-11"/>将此定义扩展到有向图，其中匹配是一组不共享起始或终止顶点的有向边。很容易知道，有向图的匹配由一组顶点不相交的简单路径和周期组成。定向网络的最大匹配可以通过在'''二部图表示 Bipartite Representation '''中使用经典的'''Hopcroft-Karp 算法 '''来高效地计算，该算法在最坏情况下的时间复杂度是O(''E'')。对于无向图，统计物理中开发的'''空腔法 Cavity Method '''研究了最大匹配的大小和数量的解析解。<ref name="Zdeborova-06">L. Zdeborová and M. Mezard, ''J. Stat. Mech.'' '''05''' (2006).</ref>Liu等人<ref name="Liu-Nature-11"/>扩展了有向图的计算范围。
+
在图论中，匹配（图论）是一组没有共同顶点的边。Liu等人<ref name="Liu-Nature-11"/>将此定义扩展到有向图，其中匹配是一组不共享起始或终止顶点的有向边。很容易知道，有向图的匹配由一组顶点不相交的简单路径和周期组成。定向网络的最大匹配可以通过在'''二部图表示 Bipartite Representation'''中使用经典的'''Hopcroft-Karp 算法'''来高效地计算，该算法在最坏情况下的时间复杂度是O(''E'')。对于无向图，统计物理中开发的'''空腔法 Cavity Method'''研究了最大匹配的大小和数量的解析解。<ref name="Zdeborova-06">L. Zdeborová and M. Mezard, ''J. Stat. Mech.'' '''05''' (2006).</ref>Liu等人<ref name="Liu-Nature-11"/>扩展了有向图的计算范围。
  
−
通过计算各种真实网络的最大匹配，Liu等人<ref name="Liu-Nature-11"/>断言驱动节点的数量主要由网络度分布<math>P(k_\mathrm{in}，k_\mathrm{out})</math>决定。他们还使用空腔方法计算了具有任意度分布的网络集合的驱动节点的平均数量。有趣的是，对于'''链图 Chain Graph '''和'''弱密集连通图 Weak Densely Connected Graph '''，两者都具有非常不同的进出度分布；Liu等人的公式<ref name="Liu-Nature-11"/>将会计算得出出<math>{n_\mathrm{D}}</math>的相同值。此外，对于许多真实世界地网络，即食物网、神经元和代谢网络，Liu等人计算的<math>{n_\mathrm{D}}^{real}</math> 和 <math>{n_\mathrm{D}}^\mathrm{rand\_degree}</math> 值的不匹配<ref name="Liu-Nature-11"/> 。值得注意的是，如果可控性纯粹由度决定，那为什么<math>{n_\mathrm{D}}^{real}</math>和<math>{n_\mathrm{D}}^\mathrm{rand\_degree}</math>对于许多现实世界的网络来说是如此不同？对于网络中的控制健壮性是否更多地受到基于度的'''中介中心性 Betweenness Centrality '''和'''紧密度中心性 Closeness Centrality '''<ref name = "Arxiv_Close_Betw"/>的影响，仍然是开放的。
+
通过计算各种真实网络的最大匹配，Liu等人<ref name="Liu-Nature-11"/>断言驱动节点的数量主要由网络度分布<math>P(k_\mathrm{in}，k_\mathrm{out})</math>决定。他们还使用空腔方法计算了具有任意度分布的网络集合的驱动节点的平均数量。有趣的是，对于'''链图 Chain Graph'''和'''弱密集连通图 Weak Densely Connected Graph'''，两者都具有非常不同的进出度分布；Liu等人的公式<ref name="Liu-Nature-11"/>将会计算得出出<math>{n_\mathrm{D}}</math>的相同值。此外，对于许多真实世界地网络，即食物网、神经元和代谢网络，Liu等人计算的<math>{n_\mathrm{D}}^{real}</math> 和 <math>{n_\mathrm{D}}^\mathrm{rand\_degree}</math> 值的不匹配<ref name="Liu-Nature-11"/> 。值得注意的是，如果可控性纯粹由度决定，那为什么<math>{n_\mathrm{D}}^{real}</math>和<math>{n_\mathrm{D}}^\mathrm{rand\_degree}</math>对于许多现实世界的网络来说是如此不同？对于网络中的控制健壮性是否更多地受到基于度的'''中介中心性 Betweenness Centrality'''和'''紧密度中心性 Closeness Centrality'''<ref name = "Arxiv_Close_Betw"/>的影响，仍然是开放的。
  
−
虽然'''稀疏图 Sparser Graph '''更难以控制<ref name="Liu-Nature-11"/><ref name = "Arxiv_Close_Betw"/> ，但是，中介中心性和紧密度中心性<ref name = "Arxiv_Close_Betw"/>，或'''度异质性 Degree Heterogeneity '''<ref name="Liu-Nature-11"/>在决定具有几乎相似的度分布的稀疏图的可控性中是否起更重要的作用？这是个有趣的问题。
+
虽然'''稀疏图 Sparser Graph'''更难以控制<ref name="Liu-Nature-11"/><ref name = "Arxiv_Close_Betw"/> ，但是，中介中心性和紧密度中心性<ref name = "Arxiv_Close_Betw"/>，或'''度异质性 Degree Heterogeneity'''<ref name="Liu-Nature-11"/>在决定具有几乎相似的度分布的稀疏图的可控性中是否起更重要的作用？这是个有趣的问题。
  
 
== 复合量子系统的控制与代数图论 ==
 
== 复合量子系统的控制与代数图论 ==
−
人们还开发了在复合量子系统的通用控制背景下的网络控制理论，其中子系统及其相互作用分别与节点和链路相关联<ref name="BG-07">{{cite journal | last=Burgarth | first=Daniel | last2=Giovannetti | first2=Vittorio | title=Full Control by Locally Induced Relaxation | journal=Physical Review Letters | publisher=American Physical Society (APS) | volume=99 | issue=10 | date=2007-09-05 | issn=0031-9007 | doi=10.1103/physrevlett.99.100501 | page=100501| arxiv=0704.3027 }}</ref>。该框架允许使用代数图论中的工具通过图的最小等级和相关概念来制定'''卡尔曼准则 Kalman's Criterion '''。<ref name="BDHSY-13">{{cite journal|last1=Burgarth|first1=Daniel|last2=D'Alessandro|first2=Domenico|last3=Hogben|first3=Leslie|last4=Severini|first4=Simone|last5=Young|first5=Michael|doi=10.1109/TAC.2013.2250075|issue=9|journal=IEEE Transactions on Automatic Control|pages=2349–2354|title=Zero forcing, linear and quantum controllability for systems evolving on networks|volume=58|year=2013}}</ref><ref name="OT-15">S. O'Rourke, B. Touri, https://arxiv.org/abs/1511.05080.</ref>
+
人们还开发了在复合量子系统的通用控制背景下的网络控制理论，其中子系统及其相互作用分别与节点和链路相关联<ref name="BG-07">{{cite journal | last=Burgarth | first=Daniel | last2=Giovannetti | first2=Vittorio | title=Full Control by Locally Induced Relaxation | journal=Physical Review Letters | publisher=American Physical Society (APS) | volume=99 | issue=10 | date=2007-09-05 | issn=0031-9007 | doi=10.1103/physrevlett.99.100501 | page=100501| arxiv=0704.3027 }}</ref>。该框架允许使用代数图论中的工具通过图的最小等级和相关概念来制定'''卡尔曼准则 Kalman's Criterion'''。<ref name="BDHSY-13">{{cite journal|last1=Burgarth|first1=Daniel|last2=D'Alessandro|first2=Domenico|last3=Hogben|first3=Leslie|last4=Severini|first4=Simone|last5=Young|first5=Michael|doi=10.1109/TAC.2013.2250075|issue=9|journal=IEEE Transactions on Automatic Control|pages=2349–2354|title=Zero forcing, linear and quantum controllability for systems evolving on networks|volume=58|year=2013}}</ref><ref name="OT-15">S. O'Rourke, B. Touri, https://arxiv.org/abs/1511.05080.</ref>
  
  

2021年7月31日 (六) 13:49的版本


图1：控制一个简单的网络。

网络可控性 Network Controllability研究的是网络的结构可控性。可控性描述了我们在有限时间内，通过合适的输入选择，引导动力系统从任何初始状态到任何期望的最终状态的能力。这个定义与我们直观的控制概念非常吻合。一般的有向加权复杂网络的可控性是近年来世界范围内许多研究小组的重点研究课题。夏尔马[1]等人最近在多种生物学网络(基因-基因、 miRNA-基因、蛋白质-蛋白质相互作用网络)上的研究，确定了骨肉瘤表现型特征的控制目标，显示了基因和蛋白质在维持肿瘤微环境中的重要作用。


背景

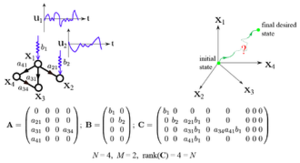
考虑复杂网络 Complex Network上的经典线性时不变动力学

[math]\displaystyle{ \dot{\mathbf{X}}(t) = \mathbf{A} \cdot \mathbf{X}(t) + \mathbf{B}\cdot \mathbf{u}(t) }[/math]

其中，向量 [math]\displaystyle{ \mathbf{X}(t)=(x_1(t),\cdots,x_N(t))^\mathrm{T} }[/math] 表示在 [math]\displaystyle{ N }[/math] 个节点的系统时间 [math]\displaystyle{ t }[/math]时的状态。

[math]\displaystyle{ N \times N }[/math] 的矩阵 [math]\displaystyle{ \mathbf{A} }[/math] 描述了系统的连接图以及各组分之间的交互强度。[math]\displaystyle{ N \times M }[/math] 矩阵 [math]\displaystyle{ \mathbf{B} }[/math] 列出了由外部控制器控制的节点。控制器通过施加给系统的时间相关向量 [math]\displaystyle{ \mathbf{u}(t) = (u_1(t),\cdots,u_M(t))^\mathrm{T} }[/math] 来实现对系统的控制。为了确定驱动节点的最小数目，[math]\displaystyle{ N_\mathrm{D} }[/math]，亦即确定对最少几个节点施加控制便足以完全控制系统的动力学进程，在这方面，Liu等人尝试了将结构控制理论 Structural Control Theory、图论 Graph Theory 和统计物理 Statistical Physics的工具的结合。[2] 他们发现[2]，完全控制一个网络所需要的最少输入或驱动节点，取决于网络的最大匹配 maximum matching，也就是不共享起始顶点和终止顶点的最大边集。从这个结论出发，一个基于入-出度分布的分析框架被开发出来，用于预测无标度网络 scale-free network和ER随即图 Erdős–Rényi Graph[2]的[math]\displaystyle{ n_\mathrm{D} =N_\mathrm{D}/N }[/math]值。[3]

同样值得关注的是，刘等人的工作[2]提出了这么一个问题[4] ：度 Degree,作为网络中一种纯粹的局部度量，能否完全描述网络的可控性？是不是即便稍微远一点的节点，就对网络的可控性没有影响？事实上，对于许多现实世界里的网络 Real-World Networks，像食物网络 Food Webs、神经元网络 Neuronal Network 和代谢网络 Metabolic Network，Liu等人计算的[math]\displaystyle{ {n_\mathrm{D}}^{real} }[/math][math]\displaystyle{ 和{n_\mathrm{D}}^\mathrm{rand\_degree} }[/math] 的值并不匹配[2]。值得注意的是。如果可控性主要是由度决定，那么为什么对于许多现实世界的网络来说，[math]\displaystyle{ {n_\mathrm{D}}^{real} }[/math] 和 [math]\displaystyle{ {n_\mathrm{D}}^\mathrm{rand\_degree} }[/math] 如此不同？他们认为[2]，这可能是由于度相关性的影响。然而，已有的研究表明[4]，网络的可控性只能通过中间性和封闭性来改变，而完全不需要使用度（图论）或度相关性 Degree Correlations。(arXiv:1203.5161v1)

示意图显示了一个有向向网络的控制。对于给定的有向网络（图a），可以计算其最大匹配：没有共同头部或尾部的最大边集。最大匹配将由一组顶点不相交的有向路径和有向环组成（请参见图b中的红色边缘）。如果一个节点是匹配边的头部，则该节点是匹配的（图b中的绿色节点）。否则，它是不匹配的（图b中的白色节点）。那些不匹配的节点是需要施加控制的节点，即驱动节点。通过向这些驱动节点注入信号，可以得到一组以起点为输入的有向路径（见图c）。这些路径被称为“茎”。得到的有向图称为U根因子连接。通过将定向周期“嫁接”到那些“茎”，人们就会得到“芽”。得到的有向图称为仙人掌 cacti（见图d）。根据结构可控性定理，由于存在跨越受控网络的cacti结构（参见图e），因此该系统是可控的。受控网络（图e）下的cacti结构（图d）是维持可控性的“骨架”。


结构可控性

结构性质的概念最早是由 Lin (1974) [5] 提出的，然后由 Glover 和 Silverman (1976)扩展。 [6][7] 主要的问题是，对于可变系统参数来说，缺乏可控性或可观测性是否是普遍存在的现象。在结构控制的框架里，系统参数要么是独立自由变量，要么是固定的0。这对于物理系统的模型是一致的，因为参数值永远不会准确地获得，零值除外，零值代表没有交互和连接。

最大匹配

在图论中，匹配（图论）是一组没有共同顶点的边。Liu等人[2]将此定义扩展到有向图，其中匹配是一组不共享起始或终止顶点的有向边。很容易知道，有向图的匹配由一组顶点不相交的简单路径和周期组成。定向网络的最大匹配可以通过在二部图表示 Bipartite Representation中使用经典的Hopcroft-Karp 算法来高效地计算，该算法在最坏情况下的时间复杂度是O(E)。对于无向图，统计物理中开发的空腔法 Cavity Method研究了最大匹配的大小和数量的解析解。[8]Liu等人[2]扩展了有向图的计算范围。

通过计算各种真实网络的最大匹配，Liu等人[2]断言驱动节点的数量主要由网络度分布[math]\displaystyle{ P(k_\mathrm{in}，k_\mathrm{out}) }[/math]决定。他们还使用空腔方法计算了具有任意度分布的网络集合的驱动节点的平均数量。有趣的是，对于链图 Chain Graph和弱密集连通图 Weak Densely Connected Graph，两者都具有非常不同的进出度分布；Liu等人的公式[2]将会计算得出出[math]\displaystyle{ {n_\mathrm{D}} }[/math]的相同值。此外，对于许多真实世界地网络，即食物网、神经元和代谢网络，Liu等人计算的[math]\displaystyle{ {n_\mathrm{D}}^{real} }[/math] 和 [math]\displaystyle{ {n_\mathrm{D}}^\mathrm{rand\_degree} }[/math] 值的不匹配[2] 。值得注意的是，如果可控性纯粹由度决定，那为什么[math]\displaystyle{ {n_\mathrm{D}}^{real} }[/math]和[math]\displaystyle{ {n_\mathrm{D}}^\mathrm{rand\_degree} }[/math]对于许多现实世界的网络来说是如此不同？对于网络中的控制健壮性是否更多地受到基于度的中介中心性 Betweenness Centrality和紧密度中心性 Closeness Centrality[4]的影响，仍然是开放的。

虽然稀疏图 Sparser Graph更难以控制[2][4] ，但是，中介中心性和紧密度中心性[4]，或度异质性 Degree Heterogeneity[2]在决定具有几乎相似的度分布的稀疏图的可控性中是否起更重要的作用？这是个有趣的问题。

复合量子系统的控制与代数图论

人们还开发了在复合量子系统的通用控制背景下的网络控制理论，其中子系统及其相互作用分别与节点和链路相关联[9]。该框架允许使用代数图论中的工具通过图的最小等级和相关概念来制定卡尔曼准则 Kalman's Criterion。[10][11]


其他参考资料

  • 可控性格拉姆矩阵


参考文献

  1. ↑ Sharma, Ankush; Cinti, Caterina; Capobianco, Enrico (2017). "Multitype Network-Guided Target Controllability in Phenotypically Characterized Osteosarcoma: Role of Tumor Microenvironment". Frontiers in Immunology (in English). 8: 918. doi:10.3389/fimmu.2017.00918. ISSN 1664-3224. PMC 5536125. PMID 28824643.
  2. ↑ 2.00 2.01 2.02 2.03 2.04 2.05 2.06 2.07 2.08 2.09 2.10 2.11 2.12 Liu, Yang-Yu; Slotine, Jean-Jacques; Barabási, Albert-László (2011). "Controllability of complex networks". Nature. Springer Science and Business Media LLC. 473 (7346): 167–173. doi:10.1038/nature10011. ISSN 0028-0836.
  3. ↑ Gates, Alexander J.; Rocha, Luis M. (2016-04-18). "Control of complex networks requires both structure and dynamics". Scientific Reports. Springer Science and Business Media LLC. 6 (1): 24456. doi:10.1038/srep24456. ISSN 2045-2322.
  4. ↑ 4.0 4.1 4.2 4.3 4.4 Banerjee, SJ; Roy, S. "Key to Network Controllability". arXiv:1209.3737.
  5. ↑ C.-T. Lin, IEEE Trans. Auto. Contr. 19(1974).
  6. ↑ R. W. Shields and J. B. Pearson, IEEE Trans. Auto. Contr. 21(1976).
  7. ↑ K. Glover and L. M. Silverman, IEEE Trans. Auto. Contr. 21(1976).
  8. ↑ L. Zdeborová and M. Mezard, J. Stat. Mech. 05 (2006).
  9. ↑ Burgarth, Daniel; Giovannetti, Vittorio (2007-09-05). "Full Control by Locally Induced Relaxation". Physical Review Letters. American Physical Society (APS). 99 (10): 100501. arXiv:0704.3027. doi:10.1103/physrevlett.99.100501. ISSN 0031-9007.
  10. ↑ Burgarth, Daniel; D'Alessandro, Domenico; Hogben, Leslie; Severini, Simone; Young, Michael (2013). "Zero forcing, linear and quantum controllability for systems evolving on networks". IEEE Transactions on Automatic Control. 58 (9): 2349–2354. doi:10.1109/TAC.2013.2250075.
  11. ↑ S. O'Rourke, B. Touri, https://arxiv.org/abs/1511.05080.


相关链接



编者推荐

集智视频

[ht]

本中文词条由信白初步参与编译，Ricky审校，糖糖编辑，如有问题，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=网络可控性&oldid=25008”