“拐点”的版本间的差异
| 第98行: | 第98行: | ||
If the second derivative, {{math|''f"{{''}}''(''x'')}} exists at {{math|''x''<sub>0</sub>}}, and {{math|''x''<sub>0</sub>}} is an inflection point for {{mvar|f}}, then {{math|''f{{''}}''(''x''<sub>0</sub>) {{=}} 0}}, but this condition is not [[Sufficient condition|sufficient]] for having a point of inflection, even if derivatives of any order exist. In this case, one also needs the lowest-order (above the second) non-zero derivative to be of odd order (third, fifth, etc.). If the lowest-order non-zero derivative is of even order, the point is not a point of inflection, but an ''undulation point''. However, in algebraic geometry, both inflection points and undulation points are usually called ''inflection points''. An example of an undulation point is {{math|''x'' {{=}} 0}} for the function {{mvar|f}} given by {{math|''f''(''x'') {{=}} ''x''<sup>4</sup>}}. | If the second derivative, {{math|''f"{{''}}''(''x'')}} exists at {{math|''x''<sub>0</sub>}}, and {{math|''x''<sub>0</sub>}} is an inflection point for {{mvar|f}}, then {{math|''f{{''}}''(''x''<sub>0</sub>) {{=}} 0}}, but this condition is not [[Sufficient condition|sufficient]] for having a point of inflection, even if derivatives of any order exist. In this case, one also needs the lowest-order (above the second) non-zero derivative to be of odd order (third, fifth, etc.). If the lowest-order non-zero derivative is of even order, the point is not a point of inflection, but an ''undulation point''. However, in algebraic geometry, both inflection points and undulation points are usually called ''inflection points''. An example of an undulation point is {{math|''x'' {{=}} 0}} for the function {{mvar|f}} given by {{math|''f''(''x'') {{=}} ''x''<sup>4</sup>}}. | ||
| − | 如果二阶导数 f"(x) 在点 {{math|''x''<sub>0</sub>}} 处存在,且 {{math|''x''<sub>0</sub>}} 是该函数的拐点,那么f"(x0)=0。然而,即使存在任意阶的导数,这也只是拐点的必要非充分条件。在这种情况下,若最低阶(第二阶以上)非零导数为奇数阶(第三阶、第五阶等) | + | 如果二阶导数 f"(x) 在点 {{math|''x''<sub>0</sub>}} 处存在,且 {{math|''x''<sub>0</sub>}} 是该函数的拐点,那么f"(x0)=0。然而,即使存在任意阶的导数,这也只是拐点的必要非充分条件。在这种情况下,若最低阶(第二阶以上)非零导数为奇数阶(第三阶、第五阶等),则该点是拐点;若最低阶非零导数为偶数阶,则该点不是拐点,而是波动点。但在代数几何中,波动点也是拐点。例如,函数 {{math|''f''(''x'') {{=}} ''x''<sup>4</sup>}} 的波动点是 {{math|''x'' {{=}} 0}} 。 |
| 第154行: | 第154行: | ||
* if {{math|''f{{'}}''(''x'')}} is zero, the point is a ''[[stationary point]] of inflection'' | * if {{math|''f{{'}}''(''x'')}} is zero, the point is a ''[[stationary point]] of inflection'' | ||
* 若 f"(x)=0,该点为驻点拐点。 | * 若 f"(x)=0,该点为驻点拐点。 | ||
| − | |||
* if {{math|''f{{'}}''(''x'')}} is not zero, the point is a ''non-stationary point of inflection'' | * if {{math|''f{{'}}''(''x'')}} is not zero, the point is a ''non-stationary point of inflection'' | ||
* 若 f"(x)≠0,该点为非驻点拐点。 | * 若 f"(x)≠0,该点为非驻点拐点。 | ||
| 第162行: | 第161行: | ||
A stationary point of inflection is not a [[local extremum]]. More generally, in the context of [[functions of several real variables]], a stationary point that is not a local extremum is called a [[saddle point#Mathematical discussion|saddle point]]. | A stationary point of inflection is not a [[local extremum]]. More generally, in the context of [[functions of several real variables]], a stationary point that is not a local extremum is called a [[saddle point#Mathematical discussion|saddle point]]. | ||
| − | + | 驻点拐点不是局部极值点。在多实变量函数中,不是局部极值点的驻点通常被称为鞍点。 | |
| − | |||
| − | |||
| − | |||
An example of a stationary point of inflection is the point {{math|(0, 0)}} on the graph of {{math|''y'' {{=}} ''x''<sup>3</sup>}}. The tangent is the {{mvar|x}}-axis, which cuts the graph at this point. | An example of a stationary point of inflection is the point {{math|(0, 0)}} on the graph of {{math|''y'' {{=}} ''x''<sup>3</sup>}}. The tangent is the {{mvar|x}}-axis, which cuts the graph at this point. | ||
| − | + | 驻点拐点例子:{{math|(0, 0)}} 为函数 {{math|''y'' {{=}} ''x''<sup>3</sup>}} 的驻点 。切线为 {{mvar|x}} 轴,在{{math|(0, 0)}}与函数相切。 | |
| − | |||
| − | |||
| 第178行: | 第172行: | ||
An example of a non-stationary point of inflection is the point on the graph of x<sup>3</sup> + ax}}, for any nonzero . The tangent at the origin is the line ax}}, which cuts the graph at this point. | An example of a non-stationary point of inflection is the point on the graph of x<sup>3</sup> + ax}}, for any nonzero . The tangent at the origin is the line ax}}, which cuts the graph at this point. | ||
| − | + | 非驻点拐点例子:{{math|(0, 0)}}为函数 {{math|''y'' {{=}} ''x''<sup>3</sup> + ''ax''}} 的非驻点({{mvar|a}}<nowiki>为任意非零常数),在原点处的切线是ax }}}}</nowiki> | |
2021年9月8日 (三) 15:24的版本
此词条由Typhoid翻译
Plot of with an inflection point at (0,0), which is also a stationary point.
拐点在(0,0) ,也是一个驻点。
模板:Cubic graph special points.svg
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave (concave downward) to convex (concave upward), or vice versa.
在微分和微分几何中,拐点(英文名为inflection point,point of infection,,flex,或者inflection,英式拼写为inflextion)是光滑平面曲线上的曲率符号改变的点。在函数图像中,拐点处函数从下凹变为上凸 ,或从上凸变为下凹。
For example, if the curve is the graph of a function y = f(x), of differentiability class C2, an inflection point of the curve is where f'', the second derivative of f, vanishes (f'' = 0) and changes its sign at the point (from positive to negative or from negative to positive).[1] A point where the second derivative vanishes but does not change its sign is sometimes called a point of undulation or undulation point.
例如,若曲线 y = f(x) 有二阶导数,那么拐点处曲线二阶导数 f'' 为0(f'' =0),并且符号改变(从正到负或从负到正)[1]。二阶导数为0但其符号不变的点有时称为波动点。
In algebraic geometry an inflection point is defined slightly more generally, as a regular point where the tangent meets the curve to order at least 3, and an undulation point or hyperflex is defined as a point where the tangent meets the curve to order at least 4.
In algebraic geometry an inflection point is defined slightly more generally, as a regular point where the tangent meets the curve to order at least 3, and an undulation point or hyperflex is defined as a point where the tangent meets the curve to order at least 4.
在代数几何中,拐点的定义更为广泛一些,如切线与曲线相交处的正则点至少为3,波动点或超高频点则定义为切线与曲线相交处至少为4。
Definition
定义
Inflection points in differential geometry are the points of the curve where the curvature changes its sign.[2][3]
For example, the graph of the differentiable function has an inflection point at (x, f(x)) if and only if its first derivative, f', has an isolated extremum at x. (This is not the same as saying that f has an extremum). That is, in some neighborhood, x is the one and only point at which f' has a (local) minimum or maximum. If all extrema of f' are isolated, then an inflection point is a point on the graph of f at which the tangent crosses the curve.
例如,当且仅当可微函数 f 的一阶导数 f' 在 x 处具有孤立极值时(而不是极值),函数在 (x, f(x))处有拐点。也就是说,在某些邻域中,x 是 f' 具有(局部)最小值或最大值的唯一点。如果所有 f' 的极值都是孤立的,那么拐点就是 f 曲线图上切线穿越曲线的点。
A falling point of inflection is an inflection point where the derivative is negative on both sides of the point; in other words, it is an inflection point near which the function is decreasing. A rising point of inflection is a point where the derivative is positive on both sides of the point; in other words, it is an inflection point near which the function is increasing.
下降拐点的两边导数都为负,即在该点附近函数值变小。上升拐点的两边导数都为正,即在该点附近函数值变大。
For an algebraic curve, a non singular point is an inflection point if and only if the intersection number of the tangent line and the curve (at the point of tangency) is greater than 2.[4]
对于一条代数曲线,当且仅当切线与曲线(在切点处)的交点数大于2时,非奇点为拐点。
The principal result is that the set of the inflection points of an algebraic curve coincides with the intersection set of the curve with the Hessian curve.
其主要结果是代数曲线拐点的集合与曲线同黑塞曲线 (Hessian curve) 的交点集合一致。
For a smooth curve given by parametric equations, a point is an inflection point if its signed curvature changes from plus to minus or from minus to plus, i.e., changes sign.
对于由参数方程组给出的光滑曲线,若某点处曲率符号改变(从正变为负或从负变为正),则该点就是拐点。
For a smooth curve which is a graph of a twice differentiable function, an inflection point is a point on the graph at which the second derivative has an isolated zero and changes sign.
对于一条二次可微函数的光滑曲线,拐点是的二次导数具有孤立零值并且改变曲率符号的点。
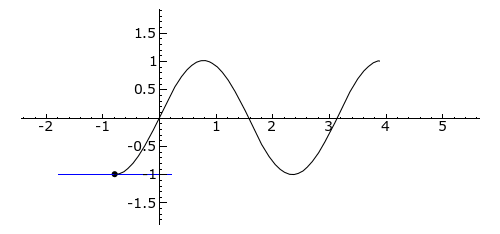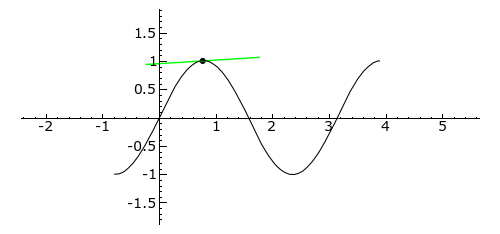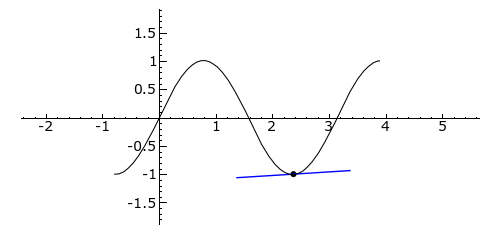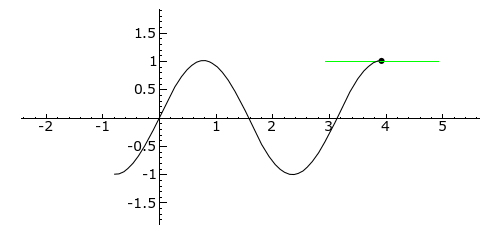
Plot of sin(2x)}} from −/4 to 5/4; the second [[derivative is (x) –4sin(2x)}}, and its sign is thus the opposite of the sign of . Tangent is blue where the curve is convex (above its own tangent), green where concave (below its tangent), and red at inflection points: 0, /2 and ]]
从-/4到5/4的 sin (2x)}的图; 第二个[[导数是(x)-4sin (2x)}] ,它的符号因此相反。切线是蓝色的,该处曲线是凸的(在它自己的切线之上) ,绿色的是凹的(在它的切线之下) ,并且红色的是拐点: 0,/2和]。
A necessary but not sufficient condition
必要非充分条件
If the second derivative, f"模板:''(x) exists at x0, and x0 is an inflection point for f, then f模板:''(x0) = 0, but this condition is not sufficient for having a point of inflection, even if derivatives of any order exist. In this case, one also needs the lowest-order (above the second) non-zero derivative to be of odd order (third, fifth, etc.). If the lowest-order non-zero derivative is of even order, the point is not a point of inflection, but an undulation point. However, in algebraic geometry, both inflection points and undulation points are usually called inflection points. An example of an undulation point is x = 0 for the function f given by f(x) = x4.
如果二阶导数 f"(x) 在点 x0 处存在,且 x0 是该函数的拐点,那么f"(x0)=0。然而,即使存在任意阶的导数,这也只是拐点的必要非充分条件。在这种情况下,若最低阶(第二阶以上)非零导数为奇数阶(第三阶、第五阶等),则该点是拐点;若最低阶非零导数为偶数阶,则该点不是拐点,而是波动点。但在代数几何中,波动点也是拐点。例如,函数 f(x) = x4 的波动点是 x = 0 。
In the preceding assertions, it is assumed that f has some higher-order non-zero derivative at x, which is not necessarily the case. If it is the case, the condition that the first nonzero derivative has an odd order implies that the sign of f模板:'(x) is the same on either side of x in a neighborhood of x. If this sign is positive, the point is a rising point of inflection; if it is negative, the point is a falling point of inflection.
前面我们假定 f 在 x 处存在高阶非零导数,但并不一定存在。如果 f 在 x 处存在高阶非零导数,第一个非零导数有奇数阶意味着f''(x)的符号在某邻域的任一边都是相同的。如果符号为正,那么这个点就是上升拐点;如果符号为负,那么这个点就是下降拐点。
Inflection points sufficient conditions:
拐点充分条件:
1) A sufficient existence condition for a point of inflection is:
1)第一充分条件:
- If f(x) is k times continuously differentiable in a certain neighborhood of a point x with k odd and k ≥ 3, while f(n)(x0) = 0 for n = 2, …, k − 1 and f(k)(x0) ≠ 0 then f(x) has a point of inflection at x0.
设函数在点 x 的某邻域 k 阶连续可微,k 为奇数且 k ≥ 3,若 f(n)(x0) = 0 ( n = 2, …, k − 1) 且 f(k)(x0) ≠ 0 ,那么点 x0 是 f(x) 的拐点。
2) Another sufficient existence condition requires f模板:''(x + ε) and f模板:''(x − ε) to have opposite signs in the neighborhood of x (Bronshtein and Semendyayev 2004, p. 231).
2) Another sufficient existence condition requires (x + ε)}} and (x − ε)}} to have opposite signs in the neighborhood of x (Bronshtein and Semendyayev 2004, p. 231).
2)第二充分条件:f''(x + ε) 和 f'' (x − ε) 在 x 邻域符号相反。
Categorization of points of inflection
拐点的分类
x4 – x}} has a 2nd derivative of zero at point (0,0), but it is not an inflection point because the fourth derivative is the first higher order non-zero derivative (the third derivative is zero as well).
x4 – x}}在点 (0,0) 处二阶导数为0,但 (0,0) 不是拐点,因为其四阶导数是一阶非零导数(三阶导数也是零)。
Points of inflection can also be categorized according to whether f模板:'(x) is zero or nonzero.
拐点也可以根据f"=(x)是否为0来进行分类。
- if f模板:'(x) is zero, the point is a stationary point of inflection
- 若 f"(x)=0,该点为驻点拐点。
- if f模板:'(x) is not zero, the point is a non-stationary point of inflection
- 若 f"(x)≠0,该点为非驻点拐点。
A stationary point of inflection is not a local extremum. More generally, in the context of functions of several real variables, a stationary point that is not a local extremum is called a saddle point.
驻点拐点不是局部极值点。在多实变量函数中,不是局部极值点的驻点通常被称为鞍点。
An example of a stationary point of inflection is the point (0, 0) on the graph of y = x3. The tangent is the x-axis, which cuts the graph at this point.
驻点拐点例子:(0, 0) 为函数 y = x3 的驻点 。切线为 x 轴,在(0, 0)与函数相切。
An example of a non-stationary point of inflection is the point (0, 0) on the graph of y = x3 + ax, for any nonzero a. The tangent at the origin is the line y = ax, which cuts the graph at this point.
An example of a non-stationary point of inflection is the point on the graph of x3 + ax}}, for any nonzero . The tangent at the origin is the line ax}}, which cuts the graph at this point.
非驻点拐点例子:(0, 0)为函数 y = x3 + ax 的非驻点(a为任意非零常数),在原点处的切线是ax }}}}
Functions with discontinuities
非连续性函数
Some functions change concavity without having points of inflection. Instead, they can change concavity around vertical asymptotes or discontinuities. For example, the function [math]\displaystyle{ x\mapsto \frac1x }[/math] is concave for negative x and convex for positive x, but it has no points of inflection because 0 is not in the domain of the function.
Some functions change concavity without having points of inflection. Instead, they can change concavity around vertical asymptotes or discontinuities. For example, the function [math]\displaystyle{ x\mapsto \frac1x }[/math] is concave for negative and convex for positive , but it has no points of inflection because 0 is not in the domain of the function.
有些函数在没有拐点的情况下也可改变凹度。他们可以通过改变垂直渐近线或非连续性来实现。例如,函数 < math > x mapsto frac1x </math > 在x为负的时候显凹性,在x为正的时候显凸性。但这个函数不具有拐点,因为0不在其定义域内。
See also
- Hesse configuration formed by the nine inflection points of an elliptic curve海塞配置 被椭圆曲线上九个拐点所组成
- Ogee, an architectural form with an inflection point S形曲线,具有一个拐点的建筑型式曲线
- Vertex (curve), a local minimum or maximum of curvature顶点,曲线的局部最小或局部最大值点
References
- ↑ 1.0 1.1 Stewart, James (2015). Calculus (8 ed.). Boston: Cengage Learning. pp. 281. ISBN 978-1-285-74062-1.
- ↑ 2.0 2.1 Problems in mathematical analysis. Baranenkov, G. S.. Moscow: Mir Publishers. 1976 [1964]. ISBN 5030009434. OCLC 21598952.
- ↑ 3.0 3.1 Bronshtein; Semendyayev (2004). Handbook of Mathematics (4th ed.). Berlin: Springer. p. 231. ISBN 3-540-43491-7.
- ↑ "Point of inflection". encyclopediaofmath.org.
Sources
Category:Differential calculus
类别: 微分
Category:Curves
类别: 曲线
Category:Analytic geometry
类别: 解析几何
This page was moved from wikipedia:en:Inflection point. Its edit history can be viewed at 拐点/edithistory