“流网络的异速标度律”的版本间的差异
| 第559行: | 第559行: | ||
具体地,我们采用如下算法来计算流网络的鲁棒性: | 具体地,我们采用如下算法来计算流网络的鲁棒性: | ||
| − | + | 1、输入流量网络F,以及对应的马尔科夫链M,将所有节点(不包括源和汇)按照它们的流量大小T<sub>i</sub>进行从大到小排序构成列表L; | |
| − | + | 2、从流网络F中删除L中的前i个节点,具体做法是: | |
| − | + | :2.1. 将M中每个删除节点所对应的列都设置为0,得到M' | |
| − | + | :2.2 根据方程T'M'+S'=T',得到新的各个节点的流量分布:T'。其中S'为源到除去删除节点以外各个节点的流量。 | |
| − | + | :2.3 计算整个网络总流量减少的百分比Δ=(ΣT-ΣT')/ΣT | |
| − | + | 3、如果Δ大于给定的阈值(如0.1),则回到2,继续删除节点 | |
| − | + | 4、否则计算出已删除节点的比例r,则r就是流网络的鲁棒性。 | |
====树==== | ====树==== | ||
| 第591行: | 第591行: | ||
对于不同商品的国际贸易网络来说,这种异速标度律指数与鲁棒性r之间的关系从图形上看,似乎更加明显。 | 对于不同商品的国际贸易网络来说,这种异速标度律指数与鲁棒性r之间的关系从图形上看,似乎更加明显。 | ||
| + | |||
| + | <br> | ||
==参考文献== | ==参考文献== | ||
2021年11月11日 (四) 15:24的版本
所谓的流网络的异速标度律(allometric scaling)表示的是指在流网络中,各个节点的通过流(Throughflow)Ti与该节点在整个网络中的影响力Ci存在着幂律关系:
[math]\displaystyle{ C_i\propto T_i^{\eta} }[/math],其中η为异速标度律指数,它可以用来衡量流网络结构的权利集中程度。当η>1的时候,我们称网络是中心化的,当η<1的时候网络是去中心化的。
研究历史
关于网络的异速标度律研究要从J.R.Banavar提出来的解释著名的Kleiber定律的模型说起(参见异速生长律)。生物学家Kleiber很早就发现在物种级别存在着生物体体积M与新陈代谢的3/4幂律关系[1],即:
[math]\displaystyle{ F\propto M^{3/4} }[/math]
为了解释这一现象,物理学家Banavar提出了一个模型(参见Banavar模型)[2],该模型假设生物体内普遍存在着空间填充的营养物质输运网络,这种网络经过漫长的进化过程,最终形成了一种最优化的结构:一棵最优化运输能力的树,树中的每个节点都有1单位耗散流,每个点的流量等于子树中节点的总个数。假设这个树的新陈代谢总流为F,树上所有边的总流量加和为M,那么就有如下异速标度律关系:
[math]\displaystyle{ F\propto M^{\frac{d}{d+1}} }[/math]
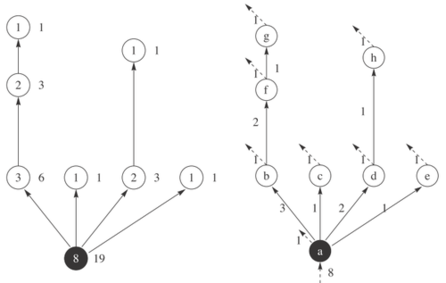
其中,d为该网络所嵌入的空间维数。下图展示了一个2维的Banavar最优树示例:
我们看到,Banavar最优树是一种对称的网络,黑色节点为根。每条边上的流量标在了旁边,可以验证,通过任意一点的流量刚好是以该节点为根的子树上的所有节点流量之和。并且每个节点的耗散流都是1。
这棵树非常对称,而且存在着自相似性。每一个节点为根的子树都与整棵树相似。如果我们计算流经某节点的流量Ai和以i为根的子树的所有流量为Ci,则能得到一个幂律关系:
[math]\displaystyle{ C_i\propto A_i^{\eta} }[/math]
对于2维的Banavar最优树来说,η为1.2945。注意,由于Banavar最优树模型每个节点的耗散流量刚好是1,所以Ai又等于子树上的节点的个数,而Ci则是子树上所有节点对应的Ai的总和,这与树的异速标度律刚好一致。
Garlaschelli的扩充
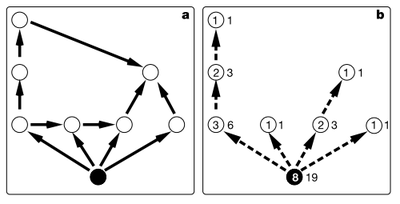
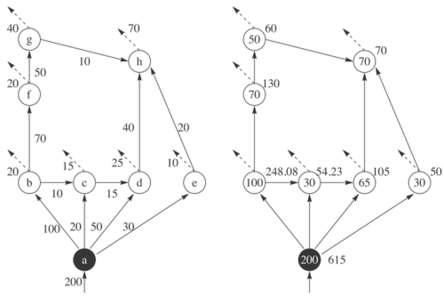
Banavar最优输运网络的幂律关系启发了Garlaschelli等人考虑是否在一般的网络中也存在着类似的关系。通过研究大量的食物网,Garlaschelli发现,如果将一个普通的食物网通过断边找到对应的生成树,并对该生成树同样计算每个节点i对应的总节点数Ai和该子树上所有节点Ai的总和Ci[3],那么也能找到普适的异速标度律法则,如下图所示:
上图展示了从左图原始网络通过断边的方式得到右侧的生成树的过程。并且对于右侧的生成树计算Ai和Ci的数值标在了右图上。其中圆圈里的数值为该节点的Ai,而圆圈旁边的数值为Ci。显然一个网络可以得到很多种不同的生成树,于是Garlaschelli不得不对所有原始网络的生成树来做平均。Garlaschelli通过分析大量的食物网,发现Ai和Ci存在着普适的幂律关系,并且幂指数都是1.13左右,如下图:
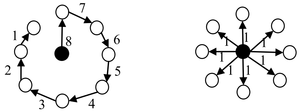
进一步,Garlashelli和Banavar的研究都指出,幂指数η可以用来衡量输运网络(食物网)的输运效率。可以证明对于树状结构来说,η数值介于1和2之间,1、2所对应的树状结构如下图所示:
在上图的两个网络中都有8个节点,按照Banavar的假设,每个节点的耗散流都是1。所以该网络根节点的总入流就是8。这些流通过连边的输运在保持流量平衡的条件下运给每一个节点。如果我们定义整个网络的输运效率是每条边上总流量的和的倒数,那么显然左图链状网络会比右图星状网络更没有效率。当网络的节点数增多趋于无穷,左边网络的幂律指数η=2,而右图星型网络的幂指数η=1。所以η越小,网络的输运效率就越高,反之输运效率就低。
虽然Garlaschelli将异速标度律扩充到了一般的有向网络上,但是他的方法存在着很多弊端:
- 必须对原始网络进行断边,这大大损失了信息。
- 没有考虑流量信息。
- 对大量生成树进行平均求得网络的幂指数显得过于任意。
流网络的异速标度律
下面我们考虑如何将异速标度律的计算扩展到一般的流网络上。所谓一般流网络的异速标度律仍旧是Ai和Ci之间的幂律关系。然而Ai和Ci的定义必须要拓广。其次,当我们考察流网络的异速标度律的时候,幂指数η的范围并不局限在1和2之间,而有可能是任意实数,因此,我们必须对η的含义进行重新解释。
基本变量
拓展异速标度律的一个重要问题就是如何对一般的流网络计算Ai和Ci这两个指标。这其中的一个主要困难就是Ai和Ci的定义都需要用到子树结构,而在一般的流网络中,我们是无法找到以i为根的子树的。要想解决这个问题,我们必须回到Banavar原始模型。在那里,Ai实际上是通过i的流量,只不过由于每个节点的耗散刚好是1,所以它才正好是子树上的节点个数。
同理,我们也可以从另一个角度理解Ci,假如所有流经i节点的粒子都被染成红色,那么Ci刚好就是存在于整个网络上的红色粒子数[4]。对于Banavar最优网络,这部分红色粒子恰好分布在以i为根的子树上了。如下图所示:
左图是一个示例的树结构,右图是计算Ai和Ci所隐含的流网络前提,其中Ai是通过节点i的流量,Ci是子树上的总流量,也就是所有红色粒子总数。
这种理解可以帮助我们扩展到一般的流网络。每个节点的Ai就是该节点的总流量Ti,如果流经i的粒子染成红色并一直保持颜色,那么,Ci就是网络中保留的红色粒子的总量。
例如对于下图左边的一般网络来说:
每个节点的Ai和Ci计算的数值如右图所示(圆圈内的数字为Ai,外面的数字为Ci)。
我们当然可以用计算机模拟的方法来计算Ci,即模拟N个粒子游走于整个网络,每个节点按照概率选择转移的分支。这样,将流经i节点的粒子标上红色,那么在某一个仿真周期,整个网络的红色粒子总数就是Ci。
但是,对于大规模的网络来说,利用多粒子模拟的方式来统计Ci会非常耗时。而我们知道,平稳的流网络任何性质都由该网络的马尔科夫矩阵决定,因此,Ci的计算也可以直接从马尔科夫链中推导出来。
下面,我们讨论Ai和Ci具体的定义和计算。
Ai
Ai定义为i节点的总流量。对于一个平衡的流网络来说,该量就等于:
[math]\displaystyle{ A_i=T_i=\sum_{j=0}^{N}f_{ji}=\sum_{j=1}^{N+1}f_{ij} }[/math]
也就是说总出流或者总入流,由于网络平衡,所以这两个量相等。既然Ai=Ti,下文我们将混用这两个变量。
Ci
按照前面的讨论,Ci是流经i节点粒子在整个网络中的分布量。如果Ci越大,显然i对整个网络的影响力就越大,因此,如果去除i节点将会对整个网络流量的分布造成比较大的影响,这可以理解为Ci的第二种定义方式。这样,我们就有两种定义和计算Ci的方法,下面分别进行介绍。
定义1
按照网络流的定义方式,考虑这样的假想实验:所有流经i的粒子都被染上红色,并且颜色不会褪去。那么可以想象,网络中所有受到i有直接影响或者间接影响的节点都会或多或少地包含一定的红色粒子。那么Ci就定义为网络中存在的红色粒子总数。由于整个流网络进入了流平衡的稳态,所以Ci在长时间来看就是一个固定的数值。根据基于马尔科夫链的流网络分析中介绍的方法,从i流出去的红色粒子到达j节点的总量就是从i到j的总流量,所以这个流量就是:
[math]\displaystyle{ t_{ij}=T_0\frac{u_{0,i}u_{i,j}}{u_{i,i}} }[/math]
那么,Ci就是把i对所有j节点的总流量(除去源和汇)求和,即:
-
[math]\displaystyle{ C_i=\sum_{j=1}^{N}t_{ij}=T_0\frac{u_{0,i}}{u_{i,i}}\sum_{j=1}^{N}u_{ij} }[/math]
(eq1)
Ci也可以按照下式来计算,(例如文献[4]中就是这样计算的): [math]\displaystyle{ C_i=(\sum_{k=1}^{N}f_{0,k}\frac{u_{ki}}{u_{i,i}})\sum_{j=1}^Nu_{ij} }[/math] 上述两种计算方法相等是因为[math]\displaystyle{ MU=U-I }[/math],所以[math]\displaystyle{ \sum_{k=0}^{N+1}m_{0,k}u_{k,i}=u_{0,i} }[/math],于是就有 [math]\displaystyle{ T_0u_{0,i}=\sum_{k=1}^{N}f_{0,k}u_{ki} }[/math],于是上述两种计算Ci的方法相等。
定义2
第二种定义Ci的方式是按照投入产出分析中的做法,假设把i节点移除,这样,原来j流向i节点的流量直接进入汇,而i到其他节点j的流量都变为0[5]。于是整个网络的流量就有可能重新动态分配,重新分配后,网络有会得到一个全新的平衡的流矩阵,这个时候每个节点的流量由原来的Tk变为了T'k。于是节点i的重要性就定义为流量减少的量,即
-
[math]\displaystyle{ C_i=\sum_{k=1}^N(T_k-T_k') }[/math]
(eq2)
事实上,根据马尔科夫链的性质,可以证明对于所有的k来说Tk-T'k都是正的。
下面我们来正式定义我们如何进行删除节点的操作。对于任意的流网络来说,它的所有特征由流量矩阵F来刻画(参看流网络),因为F处于平衡,于是,可以得到一个马尔科夫矩阵M(该矩阵不包含源和汇)。实际上这个马尔科夫矩阵决定了网络的一切性质。例如稳态时候的各个节点的流量分布,即流向量[math]\displaystyle{ T=(T_1,\cdot\cdot\cdot,T_{N}) }[/math](不包括源和汇)就是由M决定的。
下面我们删除一个节点i,这相当于在马尔科夫矩阵中将第i列全部置为0,也就是说,我们定义
[math]\displaystyle{ M_{-i}=M-\Delta M }[/math]
其中, [math]\displaystyle{ \Delta M=\left\{\begin{array}{ll} m_{ts} & \mbox {if } s=i,\\ 0 & \mbox {if } s\neq i\end{array}\right. }[/math]
于是我们就得到了一个新的马尔科夫矩阵M-i,根据这个新的马尔科夫矩阵,源的流量又会在整个网络上形成一个稳态分布:[math]\displaystyle{ T'=(T_1',\cdot\cdot\cdot,T_{N}') }[/math],这个流量向量满足:
[math]\displaystyle{ T'M_{-i}+S'=T' }[/math]
其中S'为向量[math]\displaystyle{ S'=(f_{0,1},f_{0,2},\cdot\cdot\cdot,f_{0,i-1},0,f_{0,i},\cdot\cdot\cdot,f_{0,N}) }[/math],即源到各个节点的流,但是到i节点的流等于0,由上式求出T':
[math]\displaystyle{ T'=S'\cdot (I-M_{-i})^{-1}=S'\cdot U_{-i} }[/math]
其中U-i就表示去掉i节点后形成的U矩阵。
这样,Ci就是T'与原始向量T之间差的总和,即:
[math]\displaystyle{ C_i=(1,1,\cdot\cdot\cdot,1)\cdot(T-T') }[/math]
两种定义的等价性
虽然上面给出了两种关于Ci的定义,但是我们可以证明它们是彼此等价的,也就是说这两种方法计算出的Ci严格相等。我们观察算式eq1和eq2就会发现,如果两种算法相等,那么只需要验证如下事实就可以了,即
- 定理: [math]\displaystyle{ T_0 \frac{u_{0i}}{u_{ii}}u_{ij}=T_{j}-T'_{j} }[/math]对所有的j不等于0和N+1的节点都成立就可以了。
下面给出该定理严格的数学证明:
- 首先,我们来证明一个引理:
引理:[math]\displaystyle{ (U_{-i})_{ij}=\frac{u_{ij}}{u_{ii}} }[/math],其中,[math]\displaystyle{ U_{-i}=(I-M_{-i})^{-1} }[/math],[math]\displaystyle{ M_{-i}=M-\Delta M }[/math] 证明: 因为:
- [math]\displaystyle{ U=(I-M)^{-1}, U_{-i}=(I-M_{-i})^{-1} }[/math],
所以[math]\displaystyle{ U(I-M)=I=U_{-i}(I-M_{-i}) }[/math],再根据[math]\displaystyle{ M_{-i}=M-\Delta M }[/math],这样就有:
- [math]\displaystyle{ U-U_{-i}=U\Delta M U_{-i} }[/math]
考虑第i行第j列的元素,也就是:
- [math]\displaystyle{ u_{ij}-(U_{-i})_{ij}=(U_{-i})_{ij}\sum_{k=1}^{N}u_{ik}m_{ki} }[/math]
又因为:[math]\displaystyle{ UM=U-I }[/math],所以:
- [math]\displaystyle{ \sum_{k=1}^Nu_{ik}m_{ki}=u_{ii}-1 }[/math]
于是:
- [math]\displaystyle{ u_{ij}-(U_{-i})_{ij}=(U_{-i})_{ij}(u_{ii}-1) }[/math]
所以:
- [math]\displaystyle{ (U_{-i})_{ij}=\frac{u_{ij}}{u_{ii}} }[/math],
这样,引理得证。
下面,我们来证明定理:
- 证明:设[math]\displaystyle{ S=(f_{0,1},f_{0,2},\cdot\cdot\cdot,f_{0,N}) }[/math],[math]\displaystyle{ T=(T_1,T_2,\cdot\cdot\cdot,T_N) }[/math]为流网络达到稳态时各个节点流量Ti的分布向量,则根据流平衡有:
- [math]\displaystyle{ TM+S=T }[/math]
也就是,每个节点的流等于从其它节点转移过来的入流加上从源转移过来的入流, 同样的道理,对于删除i节点后的马尔科夫矩阵,
- [math]\displaystyle{ T'M_{-i}+S'=T' }[/math],
于是,将两式相减:
- [math]\displaystyle{ TM-T'M_{-i}+S-S'=T-T' }[/math]
而我们知道[math]\displaystyle{ M_{-i}=M-\Delta M }[/math],所以:
- [math]\displaystyle{ T-T'=T(M_{-i}+\Delta M)-T'M_{-i}+S-S' }[/math]
于是,可以得到:
- [math]\displaystyle{ T-T'=(T\Delta M +S-S')\cdot (I-M_{-i})^{-1}=T_i((U_{-i})_{i,1},(U_{-i})_{i,2},\cdot\cdot\cdot,(U_{-i})_{i,N}) }[/math]
于是,该向量的第j个元素:
- [math]\displaystyle{ (T-T')_j=(T_i((U_{-i})_{i,1},(U_{-i})_{i,2},\cdot\cdot\cdot,(U_{-i})_{i,N}))_j=T_i(U_{-i})_{ij} }[/math]
又由于i节点的流量i又等于从源到i的总流量(参见基于马尔科夫链的流网络分析)。 于是,Ti又可以写作:
- [math]\displaystyle{ T_i=\phi_{0,i}u_{ii} }[/math]
而又根据引理,[math]\displaystyle{ (U_{-i})_{ij}=\frac{u_{ij}}{u_{ii}} }[/math] 所以,
- [math]\displaystyle{ (T-T')_j=\phi_{0,i}u_{ii}(U_{-1})_{ij}=\phi_{0,i}u_{ij} }[/math]
根据基于马尔可夫链的流网络分析,将首达流公式代入,就得到:
- [math]\displaystyle{ (T-T')_j=T_0\frac{u_{0i}}{u_{ii}}u_{ij} }[/math]
于是,证明了定理所述等式成立。
事实上,有一种更加简单的方法能得到证明: 因为[math]\displaystyle{ SU=T }[/math],于是有[math]\displaystyle{ \delta T_j = U_{ji}\delta S_i }[/math], [math]\displaystyle{ \delta T_i = u_{ii}\delta S_i }[/math] 得到[math]\displaystyle{ \delta T_j = u_{ji}/u_{ii}\delta T_i }[/math] 而去掉点i,相当于[math]\displaystyle{ \delta T_i = T_i = \sum S_k u_{ki} }[/math] 所以[math]\displaystyle{ \delta T_j = T_i u_{ji}/u_{ii} }[/math] 再将[math]\displaystyle{ T_i=\phi_{0,i}u_{ii} }[/math]的表达式代入即可。
η的含义
在树结构的异速标度律研究中,人们普遍认为η刻画的是网络输运效率的指标,并且η介于1和2之间,星形结构(η=1)效率最高,而链状结构(η=2)效率最低。 这样讨论η的含义有一个前提:当网络接受更大的能量流入的时候,网络的能量存储是按照η次幂的方式增长的,也就是异速标度律刻画的是流网络的异速生长律,这样η越小,当网络的流入量增加的时候,它在各条边上分布的流量增长的就会慢一些,也就是存储的能量少,因此更有效率。
然而,这个前提是有问题的,对于一般的流网络来说,η反映的是网络结构的特征,而非增长的特征。也就是说[math]\displaystyle{ C_i\propto T_i^{\eta} }[/math]并不能保证[math]\displaystyle{ TST\propto IS^{\eta} }[/math]的成立,网络的异速标度与异速生长不是一回事。
因此,我们认为η刻画的是网络的结构特征,而非动态的特征。在树的异速标度律研究中,我们已经看到当树的层数越多越瘦长的时候,网络的η越高,而越扁平的树,指数η越低。如果我们将一棵树理解成一个公司的组织结构的话,那么η越大的公司它的等级结构越森严,权利集中在大老板手里,如果η越小,则公司的管理越扁平化。所以,我们认为η刻画的是网络的集中性程度。
这种讨论也适用于一般的流网络。由于我们将Ci描述为i节点对整个网络的影响程度,而Ai描述的则是i节点的直接流量。还用公司的比喻来说,Ai说的是员工i手头所掌握的直接资源(可支配的钱、人),而Ci描述的是他在整个公司中的实际权力。这样[math]\displaystyle{ C_i\propto A_i^{\eta} }[/math]成立,就意味着随着i的升迁(Ai越来越大),它的实际权力增长的相对速度大小。η越小则增长得越慢,因此组织比较扁平化(即使大老板的能力也不见得很大),η越大则增长越快,因此组织更加集中化。
例如,有两个网络具有相同的节点数,它们的Ai和Ci分别是:Ai(1)={1,2,3,4,5}, Ci(1)={1,2,3,4,5}, Ai(2)={1,2,3,4,5}, Ci(2)={1,4,9,16,25}。也就是说这两个网络的Ai分布都一样,但是第一个网的η=1,第二个的是2。那么第一个网络中的最大节点拥有的实际权力是5,占全部网络的1/3,而第二个的是25,占全部网络的25/55=0.45比第一个网大很多。因此,第二个网络结构更加集中化。
因此,我们说,η刻画的是网络的中心化程度。扩展到流网络以后的异速标度律数值η取值范围不再局限在1到2之间,而是可以取全部实数,因此,我们根据η的范围将全部网络分为三大类:
- 当η>1,网络是中心化的
- 当η<1,网络是去中心化的
- 当η=1,网络是中性的
各种流网络的异速标度律
下面我们来列举各种流网络的异速标度律情况:
生态流量网
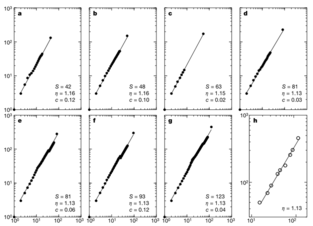
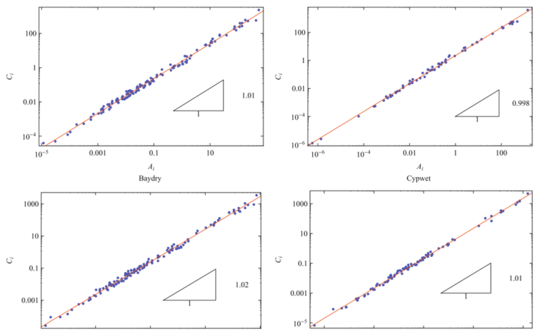
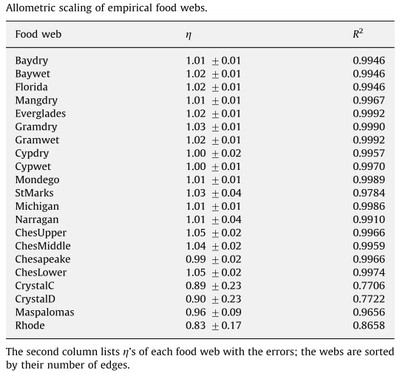
文献[4]研究了21个生态流网络的异速标度律情况,如下图所示:
图示了4个生态流网络的异速标度律在双对数坐标系下的拟合情况。我们可以看出,对于这四个网络来说,Ai、Ci的散点分布得非常接近于异速标度律那条直线,而且斜率,也就是幂指数η非常接近于1。下表则列出了更多的生态流网络的异速标度律:
我们看到,几乎所有的生态流网络遵循异速标度律的情况都比较好,而且幂指数η很接近于1,同时比1大一点点。但也有少数的网络幂指数小于1或大于1。我们说生态流网络几乎都是中性的。
点击流网络
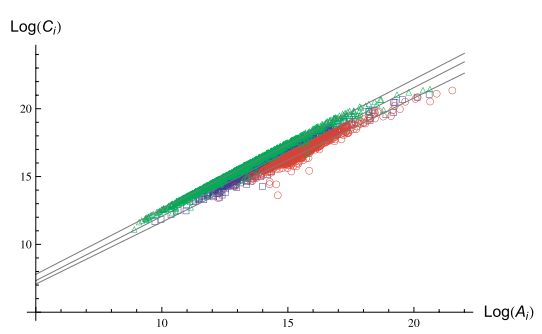
我们来看第二种网络:点击流网络[6]。这里的三个点击流网络都是文章[6]作者在不同时间从Alax网站获得的流量数据,包含了全部互联网上流量排名前1000名的所有网站。但是由于Alax网站数据的限制,每个网站的出度仅仅是10,也就是说我们只能获得从该节点流出的10条边的数据。下图展示了这三个网络Ai、Ci数据点画在双对数坐标系下的情况:
该图中不同颜色的数据点对应了三个不同的网络。这三个网络也是符合异速标度律的,它们的幂指数分别是0.95,0.92和0.96,它们都是小于1的,也就是说这些点击流构成的流网络是去中心化的。
国际贸易网
作为对比,我们再来考察另一种流网络:国际贸易网,用同样的方法可以得到2000年国际贸易网全网的异速标度指数η大约等于1.02,也是非常接近1的,即是一种中性的网络[5]。
有趣的是,国际贸易网中的流量数据还包含了具体的产品种类,也就是说,我们可以按照产品种类的不同而把原始的国际贸易流量网分解成一系列的子流网络,每个子网络对应一种产品,参见国际贸易网。我们可以分别计算这些产品对应流网络的异速标度律,从而计算它们的异速标度指数。
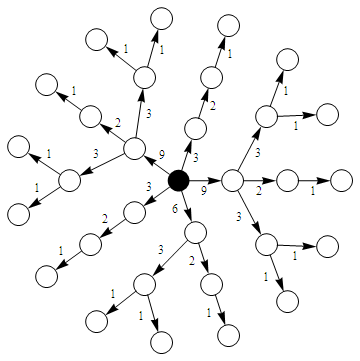
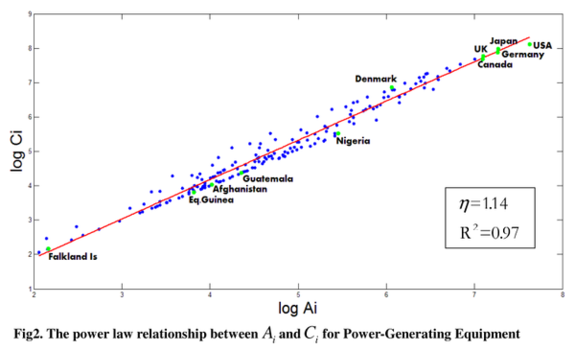
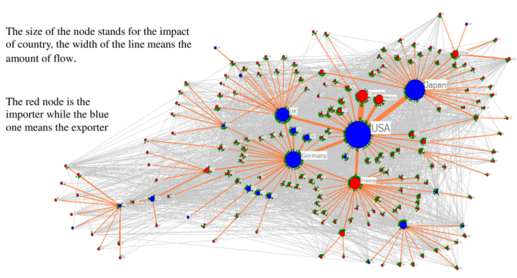
该图展示的是Power-generating equipment即发电设备这种产品的异速标度律图,其中幂指数η=1.14显著大于1。下图展示了该商品的贸易网络:
我们看到少数几个大国(美国、日本等国)作为大的出口国控制了整个网络,该网络属于中心化的。
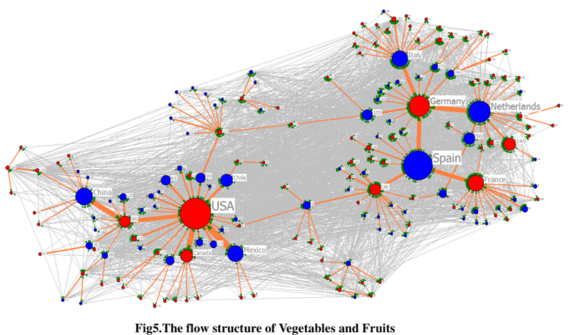
与此形成对比的是蔬菜和水果这类产品构成的贸易网络,如图:
在该网络中,那些大节点(流量Ai大,如美国、德国)基本都是进口国,即贸易逆差的国家(红色节点)。也就是说它们处于整个蔬菜水果贸易的末端,因此,流经它们的商品在整个网络中不会有很大的影响范围,所以它们的Ci不会太大,这样,该网络就会具有较小的幂指数,事实上该网络的η=1.04,远比发电设备产品的幂指数小。
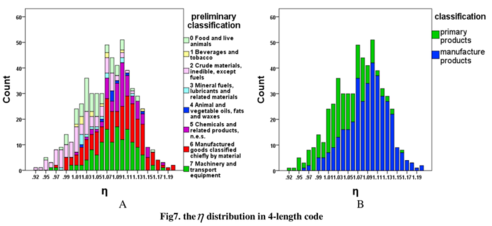
进一步,文章作者对将近800种商品子网络计算了η,得到了下面的统计图:
该图的横坐标是η数值,纵坐标是该数值在这800个商品网络中出现的频率。通过这张图,我们能看出大部分商品的η值集中在1.09附近,也就是说这些产品的贸易网络大体上是中心化的。
该文作者将频率又涂上了不同的柱状,以便表示不同的商品大分类所具备的η值范围。我们看到,大部分的工业产品集中在图形的右侧(右图),而农产品集中在左侧。所以,工业品所构成的贸易网络更加中心化——即少数国家控制了工业品的贸易流。
另外一个有趣的现象是:虽然平均来看大部分产品都是比较中心化的,但是由这些子网络合起来的整个贸易网却是比较中性的。一个可能的原因是,不同种产品的贸易可能存在着互相取长补短的作用。虽然对于A,B两种产品来说,它们都是由少数几个大国控制的中心化的网络,但是将A贸易网与B贸易网合在一起的时候,整个网络却没有那么中心化。一个可能的原因是:控制A产品的国家刚好不能控制B,而控制B的国家刚好短缺A,因此这两种网络合起来以后就没有哪个国家控制了全部的产品。因此,整个贸易网就是一种中性的结构。
指数η反映了商品的复杂性
之前树的异速标度率的研究表明,指数可以表示生成树的层级性或者扁平度,例如指数越大,生成树越趋近于链状结构,指数越小,生成树越趋近于星型结构。当我们扩展到一般的流网络中时,虽然指数的大小不在[1,2],但是指数仍然可以表示网络的层级性,是集中的还是扁平的。
指数越大,网络的结构越趋于链状结构,更加有层级性,商品就可能会在很多长的价值链上流动,例如一些需要复杂生产过程的机械产品,被国家A出口到国家B进行加工后再出口到国家C再次加工,最后到国家D才被消费;然而,指数越小,网络的结构越趋于星型结构,网络更加扁平,这种商品的流动就会有较短的价值链,例如一些农产品商品往往是由国家A出口到国家B之后直接被用来消费。
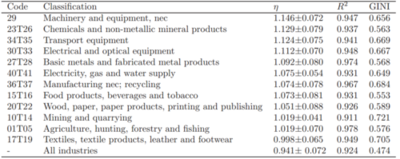
Table 1 和 Table 2 分别列出了对UN Data Set 和OECD Data Set 统计后不同的产品异速标度指数的排序,可以发现,比较精细的工业产品如机械设备、运输设备、化工产品等工业产品有较大的异速标度指数,而一些不用深加工的初级产品如农场品、原料类产品等则具有较小的指数。这就表明,异速标度指数通过对网络流结构层级性的反映,可以在一定程度上反映出商品的复杂性。
Table1.UN dataset 中SITC4编号下商品指数η(排序后)
Table2.OECD dataset 中商品指数η(排序后)
商品复杂性的一般反映
PRODY
[math]\displaystyle{ PRODY_k=\sum_{j}\frac{(x_{kj}/X_{j})}{\sum_{j}(x_{jk}/X_{j})}Y_j }[/math]
[math]\displaystyle{ PRODY_k }[/math]表示所有出口第k种产品国家的加权平均GDP,间接反映了生产产品k所需要的生产力水平。k表示第k种产品,j表示所有的国家,[math]\displaystyle{ x_{kj} }[/math]反映了国家j产品k的出口额,[math]\displaystyle{ X_j }[/math]是国家j的出口总额,[math]\displaystyle{ x_{kj}/X_{j} }[/math]是产品k的出口在国家j总出口中所占的比例,[math]\displaystyle{ \frac{(x_{kj}/X_{j})}{\sum_{j}(x_{jk}/X_{j})} }[/math]是一个对所有国家出口k的比例归一化的过程,因此[math]\displaystyle{ \frac{(x_{kj}/X_{j})}{\sum_{j}(x_{jk}/X_{j})} }[/math]表示了国家j出口产品k的相对优势。[math]\displaystyle{ Y_j }[/math]为国家j的人均GDP,表示了国家j的收入水平,同时也表示的是国家的生产水平。[math]\displaystyle{ PRODY_k }[/math]反映了出口产品k国家的平均生产力水平,因此,[math]\displaystyle{ PRODY_k }[/math]间接反映了生产产品k所需要的生产力水平。
[math]\displaystyle{ PRODY_k }[/math]越高,表示产品k所需的生产力水平越高,产品更可能是一些复杂精细的工业产品,如机械设备、动力设备等,[math]\displaystyle{ PRODY_k }[/math]越低,表示这种产品主要由生产力较低的国家生产,这种产品就更可能是一些基础产品,如农产品等。
因此,指数η应该与[math]\displaystyle{ PRODY_k }[/math]有一定的相关性.
国外附加值在总出口中的比例
OECD Dataset 中给出了每一种产品的总出口中,国外附加值所占的比例,国外附加值的比例越高,说明该类产品更多地是以价值链的形式进行贸易,产品越复杂,基础产品如农产品由A出口到B往往是直接用来消费。
指数η应该与国外附加值在总出口中的比例有一定的相关性。
指数η与PRODY及国外附加值比例的相关性
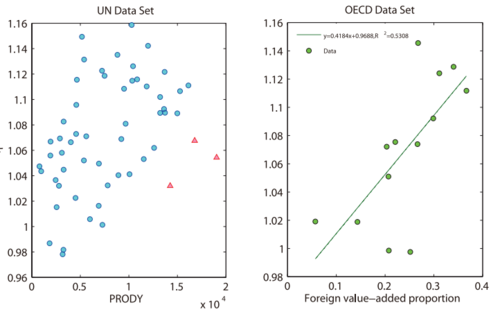
左边图中,纵轴是一种产品的指数η,横轴是PRODY,右边图中,纵轴是指数η,横轴是该种产品国外附加值占总出口的比例。
指数η与PRODY的相关性为0.37,若去掉奇异点,相关性为0.44,在0.05的显著性水平下显著相关;
指数η与国外附加值比例的相关性达到了0.692,在0.01显著性水平下显著相关。
因此,指数η可以反映一种产品的复杂性和该种产品的国外附加值比例。当一个产品需要复杂的生产过程时,就会有更多的国家参与,该种产品就会在一个长的价值链上流动,这种产品的价值中就会包含更多的国外附加值。而产品的这些性质,也都会在产品贸易网络的流结构上有所体现,当流结构更加具有层级性,更加集中时,贸易结构中就可能包含更多长的价值链,而当流结构更加扁平时,贸易中就可能包含更短的价值链。
综合
综合上述三种网络,我们可以得到下表:
| 网络 | η | 中心化与否 | 含义 |
|---|---|---|---|
| 生态流网络 | ≈1 | 中性的 | 大物种在网络中的控制力与该物种的流量成比例 |
| 点击流网络 | <1 | 去中心化的 | 大网站的影响力没有达到与流量匹配的程度 |
| 国际贸易网全网 | ≈1 | 中性的 | 大国在贸易中的控制力与该国的流量成比例 |
| 工业产品贸易网 | >1 | 中心化的 | 大国在贸易中的地位远超过了与流量匹配的程度 |
| 农业等基础产品贸易网 | <≈1 | 去中心化的 | 大国的影响力没有达到与流量匹配的程度 |
影响η指数的因素
我们已经看到不同流网络具有不同的η指数,有的时候大于1,有的时候小于1。然而,是什么影响了网络的异速标度指数η呢?文章[7]揭示了这个问题:虽然网络的拓扑结构也会影响幂指数η,但是,在流网络中,起到最关键作用的因素还要数网络的耗散律指数,而非网络的拓扑结构。这个结果多少有些反直觉。
耗散律
首先,需要指出,很多流网络都具有耗散律这一普适的规律。耗散律这一词条给出了详细的说明和结果展示。那么,影响η的各种因素中,耗散律指数γ起到了最关键的作用。为什么会是这样呢?让我们以一维的链为例来对此进行说明。
一维链结构
我们考虑如上图所示的一维链状结构,因为它比较简单,方便我们分析。
假设链状结构的耗散满足耗散律,即:
[math]\displaystyle{ D_i=c (T_i)^{\gamma} }[/math]
并且,每个节点都满足流量平衡,即:
[math]\displaystyle{ T_i=D_{i}+T_{i+1}=cT_i^{\gamma}+T_{i+1} }[/math]
利用这个递推关系,能够得到:
[math]\displaystyle{ T_i=\sum_{j=i}^ND_j }[/math]
对于这样的一维链状结构,我们又知道每个节点的Ci刚好就是i右侧所有节点的Ti之和:
[math]\displaystyle{ C_i=\sum_{j=i}^{N}T_j=\frac{1}{c^{1/\gamma}}\sum_{j=i}^{N}D_j^{\frac{1}{\gamma}} }[/math]
我们看到,Ti是i右侧节点的各个节点的耗散的总和,而Ci则是右侧节点耗散的1/γ次幂的总和。因此,若γ>1,那么随着节点沿着网络向左移动,Ti会比Ci长得快;反之,若γ<1,则Ti会比Ci长得慢。
假设网络满足异速标度律,即:
[math]\displaystyle{ C_i=b T_i^{\eta} }[/math]
其中,b是常数,那么,我们得到:
[math]\displaystyle{ \frac{1}{c^{1/\gamma}}\sum_{j=i}^{N}D_j^{\frac{1}{\gamma}}=b(\sum_{j=i}^ND_j)^{\eta} }[/math]
若γ>1,则[math]\displaystyle{ \sum_{j=i}^{N}D_j^{\frac{1}{\gamma}}\lt N^{1-\frac{1}{\gamma}}(\sum_{j=i}^{N}D_j)^{\frac{1}{\gamma}} }[/math],所以:
[math]\displaystyle{ b(\sum_{j=i}^ND_j)^{\eta}\lt N^{1-\frac{1}{\gamma}}(\sum_{j=i}^{N}D_j)^{\frac{1}{\gamma}} }[/math]
若我们忽略常数(事实上我们仅仅关心随着i的变化问题,所以常数可以忽略),则可以近似地得到:[math]\displaystyle{ \eta\lt \frac{1}{\gamma} }[/math]。同样的道理,我们可以得到,当γ>1的时候,会有:[math]\displaystyle{ \eta\gt \frac{1}{\gamma} }[/math]。而当γ=1的时候,η=1,这样,综合起来就有:
[math]\displaystyle{ \eta \left \{\begin{array}{lll} \lt \frac{1}{\gamma} & \mbox {if } \gamma\gt 1, \\ \gt \frac{1}{\gamma} & \mbox {if } \gamma\lt 1,\\ =1 & \mbox {if } \gamma=1 \end{array}\right. }[/math]
通俗地说,耗散律指数越大,左侧的大流量节点就会把越少的能量投入到后续的网络节点上,这样从该节点出发的红色粒子总量就会减少,因此Ci也就相应减少了。
生态流网络
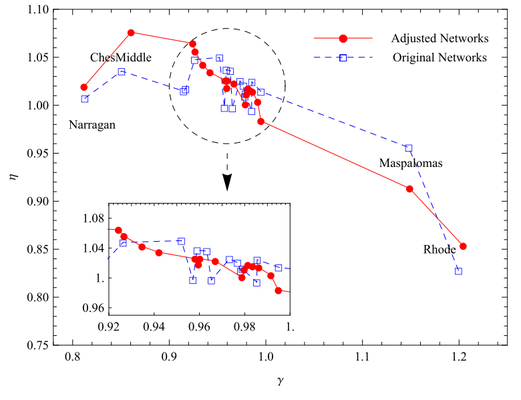
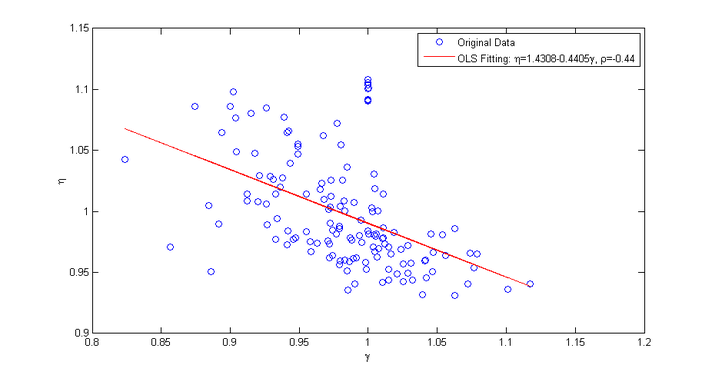
下面,我们来考察真实的生态流网络中耗散律指数与异速标度指数的关系[7]。
该图展示了19个生态流网络的耗散律指数γ与异速标度律指数η之间的关系,其中蓝色的线为原始数据点,而红色的线是经过算法调整,去除原始数据噪音后的结果。我们看到了两个指数存在着明显的负相关。但是,我们由于有噪声的存在,以及网络的结构的影响,因此,这两个指数的负相关并不严格成立。
国际贸易网
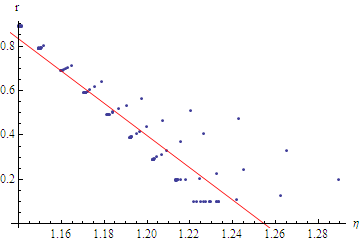
接下来,我们来研究国际贸易网的耗散律指数与异速标度指数的负相关。在国际贸易网中,由于我们可以根据不同商品而得到不同的流网络,对于每个子网络都可以计算耗散律指数和异速标度律指数,因此,我们可以把这些子网络所对应的数据点列出来画在坐标系下,如下图所示:
从该图中可以观察到,耗散律指数与异速标度律指数之间的负相关关系很明显。
网络结构
在树的异速标度律中,我们已经看到了不同的树状结构会带来不同的异速标度律指数。但是,当我们综合考虑网络拓扑结构和流量分布的时候,耗散律指数对异速标度指数的影响更加显著、明显。具体结果请参看文献[7]中的补充材料。
鲁棒性与异速标度律
上面的讨论指出,流网络的异速标度律刻画了网络的中心化的程度。指数η>1,则表示网络是中心化的,而η<1则表示网络是去中心化的。所谓的中心化程度可以理解为网络的权力集中程度。因此η越大,则网络的中央集权性就越高。
我们的一个直觉认识是,集中程度越高的网络越脆弱,也就是网络的鲁棒性就会越差。由于大量的资源集中在少数人的手中,这样只要是有意的攻击这些大尺度节点就会很容易地摧毁整个网络。这样,如果η刻画了流网络的集中性程度,那么,显然η也会跟网络的鲁棒性存在着联系。也就是η越高,流网络中心化的趋势越明显,那么网络的抗攻击性,也就是鲁棒性就会越差。这种直觉认识是对的吗?我们必须找到能够定量刻画鲁棒性的手段。
流网络的鲁棒性
复杂网络的鲁棒性问题是一个复杂网络研究中的重要问题。人们研究鲁棒性的通常做法是对网络进行攻击——即删除节点,然后考察网络的各种性质——如连通性随着节点的删除是如何变化的。删除节点的做法通常有两种:1、随机删除节点;2、蓄意攻击,即先删除重要节点(通常是度大的节点),然后删除不重要的节点……。
对于我们要研究的流网络,我们也可以采取类似的方式:蓄意攻击,即删除流量大的节点,看整个网络的流量受影响的程度如何变化。假如网络的鲁棒性越高,那么它对我们删除节点的操作并不敏感,这样,即使毁掉了网络的80%的节点,网络整个流量的变化可能也就达到了20%;而如果网络鲁棒性差,那么也许删除了仅仅10%的节点,整个网络的流量只剩下原来的1%都不到了。因此,我们可以用总流量达到原始流量1%的时候所对应的删除节点的百分比来作为整个流网络鲁棒性的衡量标准。
具体地,我们采用如下算法来计算流网络的鲁棒性:
1、输入流量网络F,以及对应的马尔科夫链M,将所有节点(不包括源和汇)按照它们的流量大小Ti进行从大到小排序构成列表L; 2、从流网络F中删除L中的前i个节点,具体做法是:
- 2.1. 将M中每个删除节点所对应的列都设置为0,得到M'
- 2.2 根据方程T'M'+S'=T',得到新的各个节点的流量分布:T'。其中S'为源到除去删除节点以外各个节点的流量。
- 2.3 计算整个网络总流量减少的百分比Δ=(ΣT-ΣT')/ΣT
3、如果Δ大于给定的阈值(如0.1),则回到2,继续删除节点 4、否则计算出已删除节点的比例r,则r就是流网络的鲁棒性。
树
为了看清楚网络的异速标度律与鲁棒性的关系,我们还是先看一种非常简单的网络:树。首先,我们按照文献[8]中的模型,通过调整参数β和θ,生成了各种形状的树。然后我们计算这些树的异速标度律指数与网络的鲁棒性之间的关系,得到下图:
我们可以清楚地看出异速标度律指数η与鲁棒性之间的负相关。其中红色拟合直线的斜率为-7.26。
生态流网络
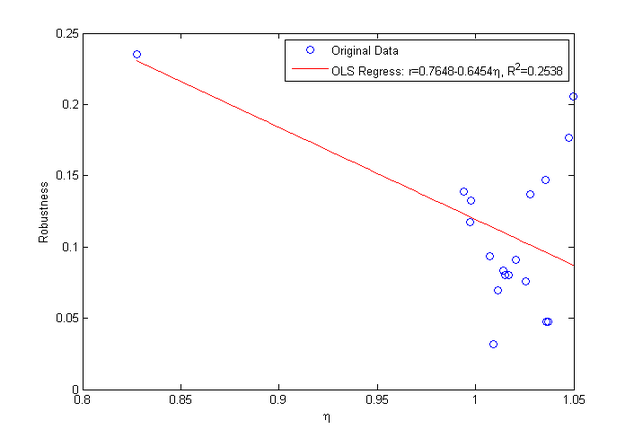
下面我们考察实际的生态流网络与网络鲁棒性之间的关系。还是采用上述21个生态流网络,我们将它们的异速标度律指数和鲁棒性的关系画出来如下图:
我们看到η和r的确存在着负相关,但是这种相关性并不十分显著,这可能是跟因为鲁棒性指标对于网络的结构而非流量的分布更敏感。
国际贸易网
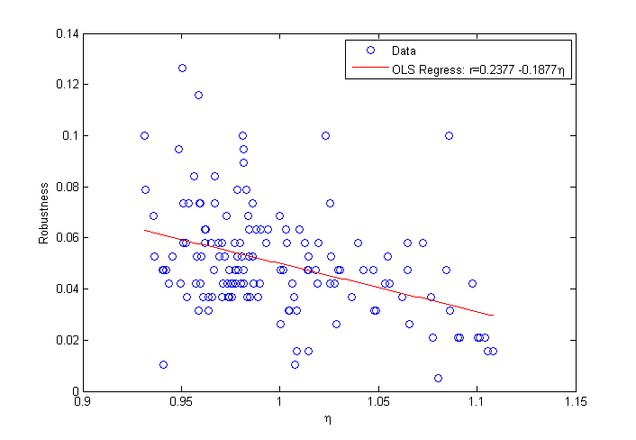
下面我们再来考察不同商品构成的贸易流网络的η与鲁棒性r之间的关系:
对于不同商品的国际贸易网络来说,这种异速标度律指数与鲁棒性r之间的关系从图形上看,似乎更加明显。
参考文献
- ↑ Kleiber, M. (1932). "Body size and metabolism". Hilgardia. 6: 315-353.
- ↑ Garlaschelli, Diego; Caldarelli, Guido; Pietronero, Luciano (2003). "Universal scaling relations in food webs". Nature. 423: 165-168.
- ↑ 4.0 4.1 4.2 Zhang, Jiang; Guo, Liangpeng (2010). "Scaling Behaviors of Weighted Food Webs as Transportation Networks". Theoretical Biology. 264: 760-770.
- ↑ 5.0 5.1 Shi, Peiteng; Luo, Jingfei; Wang, Penghao; Zhang, Jiang (2013). "Centralized Flow Structure of International Trade Networks for Different Products". International Conference on Management Science & Engineering.
- ↑ 6.0 6.1 Wu, Lingfei; Zhang, Jiang (2013). "The decentralized flow structure of clickstreams on the web". European Physics Journal B. 86: 266.
- ↑ 7.0 7.1 7.2 Zhang, Jiang; Wu, Lingfei (2013). "Allometry and Dissipation of Ecological Flow Networks". Plos One.
- ↑ Frank, F.; Murrell, D. (2005). "A simple explanation for universal scaling rela-
tions in food webs". Ecology. 86: 325-3263.
{{cite journal}}: line feed character in|title=at position 49 (help)
相关WIKI
编者推荐
课程推荐
本期课程顺应国内外网络科学研究的发展趋势,从基础、应用、Plus进阶、代码实践模块,多角度介绍更复杂更贴近现实的网络模型和结构以及高阶相互作用动力学。
本讲座主要包括流网络的理论框架、应用案例、延展与讨论内容板块。