“因果涌现”的版本间的差异
(→应用) |
|||
| 第81行: | 第81行: | ||
====在生物中的应用==== | ====在生物中的应用==== | ||
| + | |||
| + | ==== 在人工智能中的应用(编写中) ==== | ||
| + | 面向方面软件中的因果涌现 | ||
===不同的因果涌现框架=== | ===不同的因果涌现框架=== | ||
2022年6月22日 (三) 08:44的版本
此词条是由张江老师提出,将由因果涌现社区成员共同完成。
目前需要将每个模块的重点参考文献,以及要表述的重点说明清楚,让大家认领相关的知识整理,最后统一成一个完整的词条。
所谓的因果涌现是指动力系统的一类特殊的涌现现象,即系统在宏观尺度会展现出更强的因果特性。因此,因果涌现可以用因果性来定量刻画涌现这一通常难以刻画的复杂系统中的重要概念。
特别的,对于一类马尔可夫动力学系统来说,在对其状态空间进行适当的粗粒化以后,所形成的宏观动力学会展现出比微观更强的因果特性,即称该系统发生了因果涌现。这里,所谓的马尔可夫动力学系统是指系统在某一时刻的状态仅仅依赖于系统上一时刻所处的状态,而与更早的状态无关。所谓的粗粒化是指对系统的状态空间进行约简的一种方法,它往往可以表示为一个具有降维特征的函数映射。所谓的宏观动力学是指在被粗粒化后的新状态空间上的随附的(supervenes)动力学,它完全决定于微观的动力学和粗粒化方式。关于因果特性的强弱一般可以用有效信息(Effective Information,简称EI)来衡量。因果涌现这一概念最早由美国理论神经生物学家Erik Hoel于2009年提出。
历史
基本概念
现在关于因果涌现的讨论大多集中在离散状态的马尔可夫动力学系统,并且使用有效信息来对动力学的因果性进行衡量。接下来,我们将详细介绍关于因果涌现定义中的每个要素。
马尔可夫动力学
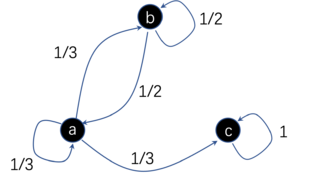
所谓的马尔可夫动力学是指系统的下一时刻状态只依赖于上一时刻的状态,并且与再之前的状态无关。马尔可夫动力学可以区分为离散时间、连续时间,离散状态、连续状态,以及它们的组合等多种。例如,如下的概率转移矩阵就定义了一个离散状态、离散空间上的马尔可夫动力学[math]\displaystyle{ P(S_{t+1}|S_{t}) }[/math]:
| states | a | b | c |
|---|---|---|---|
| a | 1/3 | 1/3 | 1/3 |
| b | 1/2 | 1/2 | 0 |
| c | 0 | 0 | 1 |
这是一个离散状态离散([math]\displaystyle{ S=\{a,b,c\} }[/math])时间的马尔可夫动力学中的状态概率转移表,其中每一行、列都对应一个状态,第i行第j列表示状态从第i个状态转移到第j个状态的概率。我们也可以等价地用状态转移图来表示。
目前对因果涌现的讨论大多集中于这种离散状态、离散时间的马尔可夫动力学。
当然,还存在着连续时间、连续状态的马尔可夫动力学,例如朗之万方程:
[math]\displaystyle{ \frac{dX}{dt} = a X + \xi }[/math]
其中[math]\displaystyle{ X }[/math]为一随机变量,可以从所有实数中取值,a为常数,[math]\displaystyle{ \xi }[/math]为一高斯噪声。
实例
可参考PNAS Erik的那篇经典的因果涌现文章:Macro beats Micro
状态空间的因果涌现
离散布尔动力学网络上的因果涌现
时域空间上的因果涌现
连续空间上的因果涌现
可参考Erik的Causal Geometry文章
关于因果的度量
可参考Erik的最新文章:CAUSAL EMERGENCE IS WIDESPREAD ACROSS MEASURES OF CAUSATION
应用
在复杂网络上的应用
见第一季读书会列表
在生物中的应用
在人工智能中的应用(编写中)
面向方面软件中的因果涌现
不同的因果涌现框架
Reconciling。。。