“神经雪崩”的版本间的差异
Spidey0o0Zheng(讨论 | 贡献) (撤销Spidey0o0Zheng(讨论)的版本33020) 标签:撤销 |
Spidey0o0Zheng(讨论 | 贡献) (撤销Spidey0o0Zheng(讨论)的版本33019) 标签:撤销 |
||
| 第25行: | 第25行: | ||
P(S)=kS^{-\alpha}\, | P(S)=kS^{-\alpha}\, | ||
</math> | </math> | ||
| + | |||
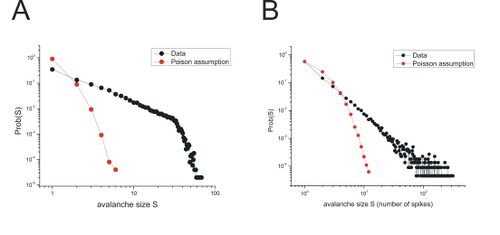
其中<math>P(S)</math>是观察到大小为<math>S</math>的雪崩的概率,<math>\alpha</math>是给出对数图中幂律斜率的指数,<math>k</math>是比例常数。对于切片培养实验,[[局部场电位]]雪崩的大小分布的指数<math>\alpha\approx 1.5 </math>,但在不同阵列的尖峰记录中,指数<math>\alpha\approx2.1</math>。指数差异背后的原因仍在探索中。需要注意的是,如果每个电极上的活动是独立驱动的,则幂律分布不是预期的分布。非耦合类泊松过程的集合将导致事件大小的指数分布。此外,虽然神经科学多年来在单个时间序列数据的时间相关性中报告了幂律(例如,[http://www.scholarpedia.org/article/Electroencephalogram 脑电图]的功率谱(Linkenkaer-Hansen等人,2001;Worrell等人,2002),峰值计数统计中的[https://en.wikipedia.org/wiki/Fano_factor Fano]或[https://en.wikipedia.org/wiki/Allan_variance Allan]因子(Teich等人,1997),神经递质分泌时间(Lowen等人,1997),[http://www.scholarpedia.org/article/Ion_channel 离子通道][http://www.scholarpedia.org/article/Fluctuations 波动](Toib等人,1998),神经元培养中的爆发间期(Segev等人,2002)),从多电极数据中观察到的相互作用中未观察到。因此,神经雪崩是从分布式网络中的集体过程中产生的。 | 其中<math>P(S)</math>是观察到大小为<math>S</math>的雪崩的概率,<math>\alpha</math>是给出对数图中幂律斜率的指数,<math>k</math>是比例常数。对于切片培养实验,[[局部场电位]]雪崩的大小分布的指数<math>\alpha\approx 1.5 </math>,但在不同阵列的尖峰记录中,指数<math>\alpha\approx2.1</math>。指数差异背后的原因仍在探索中。需要注意的是,如果每个电极上的活动是独立驱动的,则幂律分布不是预期的分布。非耦合类泊松过程的集合将导致事件大小的指数分布。此外,虽然神经科学多年来在单个时间序列数据的时间相关性中报告了幂律(例如,[http://www.scholarpedia.org/article/Electroencephalogram 脑电图]的功率谱(Linkenkaer-Hansen等人,2001;Worrell等人,2002),峰值计数统计中的[https://en.wikipedia.org/wiki/Fano_factor Fano]或[https://en.wikipedia.org/wiki/Allan_variance Allan]因子(Teich等人,1997),神经递质分泌时间(Lowen等人,1997),[http://www.scholarpedia.org/article/Ion_channel 离子通道][http://www.scholarpedia.org/article/Fluctuations 波动](Toib等人,1998),神经元培养中的爆发间期(Segev等人,2002)),从多电极数据中观察到的相互作用中未观察到。因此,神经雪崩是从分布式网络中的集体过程中产生的。 | ||
2022年7月23日 (六) 02:43的版本
此词条由神经动力学读书会词条梳理志愿者Spidey0o0Zheng翻译审校,未经专家审核,带来阅读不便,请见谅。
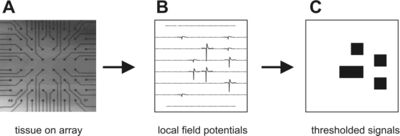
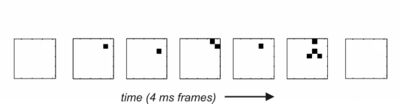
神经雪崩是神经元网络中的一连串爆发性活动,其大小分布可以用幂律来近似,如临界沙堆模型(Bak等人,1987)。神经雪崩见于培养的和急性皮质切片(Beggs和Plenz,2003;2004)。在这些新皮层切片中,活动的特点是持续几十毫秒的短暂爆发,中间有几秒钟的静止期。当用多电极阵列观察时,在爆发期间被驱动超过阈值的电极数量近似于幂律分布。虽然这种现象具有高度的稳定性和可重复性,但它与完整大脑中的生理过程的关系目前还不清楚。
实验观察
幂律尺寸分布
这个片段说明,多通道数据可以被分解为没有活动的帧和至少有一个活动电极的帧,这些电极可能接收来自几个神经元的活动。由非活动帧包围的连续活动帧序列可以称为雪崩。所示的雪崩例子的大小为9,因为这是被驱动超过阈值的电极总数。雪崩大小的分布方式几乎符合幂律分布。由于阵列中的电极数量有限,幂律在阵列大小为60之前就开始向下弯曲切断,但是对于更大的电极阵列,可以看到幂律会延伸得更远。
幂律分布的公式是:
- [math]\displaystyle{ P(S)=kS^{-\alpha}\, }[/math]
其中[math]\displaystyle{ P(S) }[/math]是观察到大小为[math]\displaystyle{ S }[/math]的雪崩的概率,[math]\displaystyle{ \alpha }[/math]是给出对数图中幂律斜率的指数,[math]\displaystyle{ k }[/math]是比例常数。对于切片培养实验,局部场电位雪崩的大小分布的指数[math]\displaystyle{ \alpha\approx 1.5 }[/math],但在不同阵列的尖峰记录中,指数[math]\displaystyle{ \alpha\approx2.1 }[/math]。指数差异背后的原因仍在探索中。需要注意的是,如果每个电极上的活动是独立驱动的,则幂律分布不是预期的分布。非耦合类泊松过程的集合将导致事件大小的指数分布。此外,虽然神经科学多年来在单个时间序列数据的时间相关性中报告了幂律(例如,脑电图的功率谱(Linkenkaer-Hansen等人,2001;Worrell等人,2002),峰值计数统计中的Fano或Allan因子(Teich等人,1997),神经递质分泌时间(Lowen等人,1997),离子通道波动(Toib等人,1998),神经元培养中的爆发间期(Segev等人,2002)),从多电极数据中观察到的相互作用中未观察到。因此,神经雪崩是从分布式网络中的集体过程中产生的。
雪崩的含义 Implications of avalanches
When a tunable system operates in a regime where it produces power law distributions, it is said to be operating at the critical point. Strictly speaking, only infinitely large systems can operate at the critical point, but here the term “critical” is used to describe behavior in finite systems that would approach criticality if they were extended to unlimited sizes. The power law avalanche size distribution has potential implications for information processing in neural networks in these four areas:
- Information transmission. When neural networks are tuned to the critical point, they have optimal information transmission (Beggs and Plenz, 2003; Bertschinger and Natschlager, 2004; Kinouchi and Copelli, 2006), because there is a balance between strong signal propagation and resistance to saturation.
- Information storage. When a recurrent network based on a branching process is tuned to the critical point, the number of significantly repeating avalanche patterns is maximized (Haldeman and Beggs, 2005). At the critical point, there is a mixture of strong and weak connections, allowing for a variety of independently stable patterns of activity.
- Computational power. By changing the variance in synaptic weights in a spiking network model, Bertschinger and Natschlager (Bertschinger and Natschlager 2004) were able to produce networks that showed damped, sustained, and expanding activity. These regimes correspond to subcritical, critical, and supercritical dynamics respectively. They found that networks tuned to the critical point performed more effectively on a broad range of computational tasks than networks that were tuned to have either subcritical or supercritical dynamics.
- Stability. When a recurrent, branching network model is tuned to the critical point, it produces largely parallel trajectories, meaning that the network is at the edge of stability (Bertschinger and Natschlager, 2004; Haldeman and Beggs, 2005). In this case, trajectories are still stable and yet are controllable with minor corrective inputs.
Optimizing all of these information processing tasks may occur simultaneously when a network operates near the critical point, where neuronal avalanches occur.
神经雪崩与其他系统的关系
Power law distributions of event sizes are often seen in complex phenomena including earthquakes, phase transitions, percolation, forest fires, financial market fluctuations, avalanches in the game of life and a host of others (Bak, 1996). In some specific cases, this similarity appears to be more than superficial. For example, earthquake models incorporate local rules in which forces at one site are distributed to nearest neighbors without dissipation. This conservation of forces is similar to the conservation of probabilities in the critical branching model described above. This suggests that conservation of synaptic strengths, as reported in (Royer and Pare, 2003) could be a mechanism responsible for maintaining a network near the critical point. In a related idea, simulations indicate that networks can be kept nearly critical when the total sum of synaptic strengths hovers near a constant value (Hsu and Beggs, 2006). This could be accomplished through a mechanism like synaptic scaling (Turrigiano and Nelson, 2000), which has been observed experimentally. Finally, recently "burned" areas in forest fire models are refractory, while unburned areas are more likely to ignite. This balance of refractoriness and excitability combine to maintain the system near the critical point. Recent models of neuronal avalanches (Levina, Herrmann and Geisel, 2005) have suggested that short-term synaptic depression and facilitation may also serve to drive neuronal networks toward the critical point where avalanches occur. Thus, an understanding of power laws in diverse complex systems can suggest mechanisms that might underlie criticality in neuronal networks.
A simple electronic model of avalanche generation consists of a two-dimensional array of neon lamps, each one connected to a resistor towards a global DC control voltage and capacitively coupled to its von Neumann neighbors. Neon lamps possess rich dynamical properties: as the applied voltage changes, the transition between the "on" and "off" phases is at the same time significantly hysteretic and stochastic (Dance, 1968). The system displays two phases, [math]\displaystyle{ I }[/math] and [math]\displaystyle{ II }[/math], respectively characterized by low and high event rate and spatiotemporal order: the transition between them is strongly hysteretic, hence unequivocally first-order. Nevertheless, close to the spinal point of the [math]\displaystyle{ I\rightarrow II }[/math] transition, critical precursors emerge in the form of avalanches (Fig. 8) having the same scaling exponents characterizing neural activity, namely [math]\displaystyle{ \alpha\approx3/2 }[/math] for size and [math]\displaystyle{ \alpha\approx2 }[/math] for duration (Minati et al., 2016).
外部链接和致谢
这项工作的撰写和图中的实验得到了美国国家科学基金会的资助和印第安纳大学的资助,约翰·贝格斯(John Beggs)的资助号为0343636。关于神经雪崩的最初工作是在迪特玛·普伦茨(Dietmar Plenz)的实验室完成的,由美国国立卫生研究院的院内研究项目资助。
参考文献
- Bak, P. (1996). How nature works: the science of self-organized criticality. New York, NY, USA, Copernicus.
- Bak P, Tang C, Wiesenfeld K (1987). Self-organized criticality: an explanation of the 1/f noise. Phys Rev Lett 59:381–384.
- Beggs, J. M. and D. Plenz (2003). Neuronal avalanches in neocortical circuits. J Neurosci 23(35): 11167-77.
- Beggs, J. M. and D. Plenz (2004). Neuronal avalanches are diverse and precise activity patterns that are stable for many hours in cortical slice cultures. J Neurosci 24(22): 5216-29.
- Bertschinger, N. and T. Natschlager (2004). "Real-time computation at the edge of chaos in recurrent neural networks." Neural Comput 16(7): 1413-36.
- Dance J. N. (1968). "Cold Cathode Tubes." Iliffe, London, UK.
- Eurich CW, Herrmann JM, Ernst UA (2002). Finite-size effects of avalanche dynamics. Phys Rev E Stat Nonlin Soft Matter Phys 66:066137.
- Haldeman, C, Beggs, JM (2005). Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys Rev Lett, 94: 058101.
- Harris TE (1989). The theory of branching processes. New York: Dover.
- Herz AV, Hopfield JJ (1995). Earthquake cycles and neural reverberations: collective oscillations in systems with pulse-coupled threshold elements. Phys Rev Lett 75:1222–1225.
- Hsu D, Beggs JM (2006). Neuronal avalanches and criticality: A dynamical model for homeostasis. Neurocomputing 69(1134-1136).
- Kinouchi O, Copelli M (2006). Optimal dynamic range of excitable networks at criticality. Nature Physics 2:348-351.
- Levina A, Herrmann JM, Geisel T (2005). Dynamical synapses give rise to a power law distribution of neuronal avalanches. Neural Information Processing Systems (NIPS) http://books.nips.cc/papers/files/nips18/NIPS2005_0646.pdf
- Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ (2001). Long-range temporal correlations and scaling behavior in human brain oscillations. J Neurosci 21:1370–1377.
- Lowen SB, Cash SS, Poo MM, Teich MC (1997). Quantal neurotransmitter secretion rate exhibits fractal behavior. J Neurosci 17:5666–5677.
- Minati, L; de Candia, A; Scarpetta, S. "Critical phenomena at a first-order phase transition in a lattice of glow lamps: Experimental findings and analogy to neural activity". Chaos. 26: 073103. doi:10.1063/1.4954879.
- Petermann T, Lebedev M, Nicolelis M, Plenz D (2006). Neuronal avalanches in vivo. Society for Neuroscience Abstracts.
- Royer S, Pare D (2003). Conservation of total synaptic weight through balanced synaptic depression and potentiation. Nature 422(6931):518-22.
- Segev R, Benveniste M, Hulata E, Cohen N, Palevski A, Kapon E, Shapira Y, Ben Jacob E (2002). Long term behavior of lithographically prepared in vitro neuronal networks. Phys Rev Lett 88:118102.
- Stewart CV, Plenz D (2006). Inverted-U profile of dopamine-NMDA-mediated spontaneous avalanche recurrence in superficial layers of rat prefrontal cortex. J Neurosci. 2006 Aug 2;26(31):8148-59.
- Teich MC, Heneghan C, Lowen SB, Ozaki T, Kaplan E (1997). Fractal character of the neural spike train in the visual system of the cat. J Opt Soc Am A Opt Image Sci Vis. 1997 Mar;14(3):529-46.
- Toib A, Lyakhov V, Marom S (1998). Interaction between duration of activity and time course of recovery from slow inactivation in mammalian brain Na_ channels. J Neurosci 18:1893–1903.
- Torre V (2006) Talk at NeuroIT conference in Genoa, Italy: http://www.neuroengineering.it/download/20.Torre.pdf
- Turrigiano GG, and Nelson SB (2000). Hebb and homeostasis in neuronal plasticity. Curr Opin Neurobiol 10:358-364.
- Vogels, T. P., K. Rajan and L. F. Abbott (2005). Neural network dynamics. Annu Rev Neurosci 28: 357-76.
- Worrell GA, Cranstoun SD, Echauz J, Litt B (2002). Evidence for self-organized criticality in human epileptic hippocampus. NeuroReport 13:2017–2021.
Internal references
- Valentino Braitenberg (2007) Brain. Scholarpedia, 2(11):2918.
- Eugene M. Izhikevich (2006) Bursting. Scholarpedia, 1(3):1300.
- Olaf Sporns (2007) Complexity. Scholarpedia, 2(10):1623.
- Gregoire Nicolis and Catherine Rouvas-Nicolis (2007) Complex systems. Scholarpedia, 2(11):1473.
- James Meiss (2007) Dynamical systems. Scholarpedia, 2(2):1629.
- Paul L. Nunez and Ramesh Srinivasan (2007) Electroencephalogram. Scholarpedia, 2(2):1348.
- Robert Kozma (2007) Neuropercolation. Scholarpedia, 2(8):1360.
- Philip Holmes and Eric T. Shea-Brown (2006) Stability. Scholarpedia, 1(10):1838.
See also
Avalanches, Complexity, Complex Systems, Game of Life, Neuropercolation, Self-organized criticality, Statistical Mechanics of Neocortex