神经雪崩

此词条由神经动力学读书会词条梳理志愿者Spidey0o0Zheng翻译审校，未经专家审核，带来阅读不便，请见谅。

图1：数据表示的示意图。超过三个标准差的局部场电位（LFPs）用黑色方块表示。

图2：急性皮层切片中的神经雪崩。

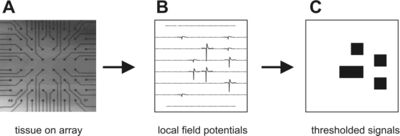
神经雪崩是神经元网络中的一连串爆发性活动，其大小分布可以用幂律来近似，如临界沙堆模型（Bak等人，1987）。神经雪崩见于培养的和急性皮质切片（Beggs和Plenz，2003；2004）。在这些新皮层切片中，活动的特点是持续几十毫秒的短暂爆发，中间有几秒钟的静止期。当用多电极阵列观察时，在爆发期间被驱动超过阈值的电极数量近似于幂律分布。虽然这种现象具有高度的稳定性和可重复性，但它与完整大脑中的生理过程的关系目前还不清楚。

实验观察

图3：雪崩示例。显示了7个帧，其中每个帧代表电极阵列在一个4毫秒的时间布长中的活动。雪崩是一系列连续的活动帧，开始和结束均是空白帧。雪崩的大小是由活动电极的总数决定的。这里显示的雪崩的大小为9。

幂律尺寸分布

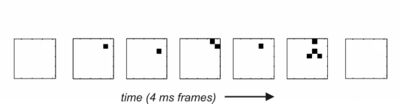
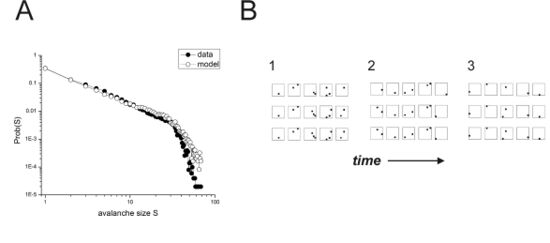
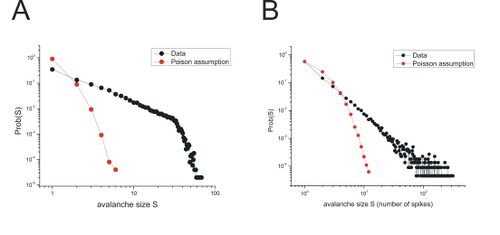
这个片段说明，多通道数据可以被分解为没有活动的帧和至少有一个活动电极的帧，这些电极可能接收来自几个神经元的活动。由非活动帧包围的连续活动帧序列可以称为雪崩。所示的雪崩例子的大小为9，因为这是被驱动超过阈值的电极总数。雪崩大小的分布方式几乎符合幂律分布。由于阵列中的电极数量有限，幂律在阵列大小为60之前就开始向下弯曲切断，但是对于更大的电极阵列，可以看到幂律会延伸得更远。

图4：雪崩尺寸分布。 A，用60个电极阵列记录的急性切片局部场电位的大小分布，以对数空间绘制。实际数据显示为黑色，而泊松模型的输出显示为红色。在泊松模型中，每个电极的发射速度与实际数据中看到的相同，但独立于所有其他电极。注意这两条曲线之间的巨大差异。实际数据在1-35的尺寸下几乎是一条直线；在这一点之后，存在由电极阵列大小引起的截止。直线表示幂律，表明网络在临界点附近运行（未发表的数据由W. Chen, C. Haldeman, S. Wang, A. Tang, J.M. Beggs记录）。 B，尖峰的雪崩大小分布可以用概率超过三个数量级的直线近似，没有A组中看到的尖锐的截止点。数据是用512个电极阵列从浸泡在高钾和零镁的急性皮层切片中收集的（A. Litke, S. Sher, M. Grivich, D. Petrusca, S. Kachiguine, J. M. Beggs未发表的工作）。峰值以-3个标准差设定阈值，并且未进行分类。数据在1.2ms时合并，以匹配60μm的短电极间距离。从培养基中记录的皮层切片培养中也获得了类似于A和B的结果。

幂律分布的公式是:

[math]\displaystyle{ P(S)=kS^{-\alpha}\, }[/math]

其中[math]\displaystyle{ P(S) }[/math]是观察到大小为[math]\displaystyle{ S }[/math]的雪崩的概率，[math]\displaystyle{ \alpha }[/math]是给出对数图中幂律斜率的指数，[math]\displaystyle{ k }[/math]是比例常数。对于切片培养实验，局部场电位雪崩的大小分布的指数[math]\displaystyle{ \alpha\approx 1.5 }[/math]，但在不同阵列的尖峰记录中，指数[math]\displaystyle{ \alpha\approx2.1 }[/math]。指数差异背后的原因仍在探索中。需要注意的是，如果每个电极上的活动是独立驱动的，则幂律分布不是预期的分布。非耦合类泊松过程的集合将导致事件大小的指数分布。此外，虽然神经科学多年来在单个时间序列数据的时间相关性中报告了幂律（例如，脑电图的功率谱（Linkenkaer-Hansen等人，2001；Worrell等人，2002），峰值计数统计中的Fano或Allan因子（Teich等人，1997），神经递质分泌时间（Lowen等人，1997），离子通道波动（Toib等人，1998），神经元培养中的爆发间期（Segev等人，2002）），从多电极数据中观察到的相互作用中未观察到。因此，神经雪崩是从分布式网络中的集体过程中产生的。

重复的雪崩模式

图5：急性切片的重复雪崩的家族。每个家庭（1-4）显示了一组三个类似的雪崩。与50组随机数据相比，每组内的相似性高于偶然预期。重复雪崩也发生在皮层切片培养中，其中平均有30±14（平均±标准差）个不同的可重复雪崩家族，每个家族包含约23个雪崩（Beggs和Plenz，2004）。重复雪崩在10小时内是稳定的，时间精度为4ms，这表明它们可以作为神经网络中存储信息的基底。

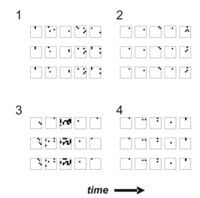
临界沙堆模型中的雪崩在其形成的模式中是随机的，与之相比，局部场电位的雪崩发生的时空模式比预期的偶然性更频繁（Beggs和Plenz，2004）。图中显示了一个急性皮层切片的几个这样的模式。这些模式在长达10个小时的时间内是可重复的，其时间精度为4ms（Beggs和Plenz，2004）。这些模式的稳定性和精确性表明，神经雪崩可以被神经网络用作存储信息的基底。在这个意义上，雪崩似乎与在动物执行认知任务时在体内观察到的动作电位序列相似。目前还不清楚体内数据的重复活动模式是否也是雪崩。

普遍性

在上述示例中，雪崩是在浸泡在培养基中的皮层切片培养中产生的，但当急性皮层切片在含有多巴胺激动剂和NMDA（Beggs和Plenz，2003；Stewart和Plenz，2006）或高K⁺和低Mg²⁺的人工脑脊液中浸泡时，也可能在急性皮层切片中产生雪崩。诱发雪崩的不同方式表明，它们不仅仅局限于一组实验条件。

其他系统中的初步报告

在离体水蛭神经节（V.Torre，conference talk）的棘波和分离皮层培养的棘波（L.Bettencourt；R.Alessio，personal communications）中也观察到序列大小的幂律分布，这表明雪崩现象可能在体外制剂中相当普遍。初步报告还表明，在清醒和休息的灵长类动物的表层皮层中存在雪崩（Petermann等人，2006年）。这些报告尚未发表，在此仅表明研究人员目前正在探索各种制剂中的雪崩概念。

雪崩模型

图6：分支过程的三个阶段。分支过程的三种状态。顶部，当分支参数[math]\displaystyle{ \sigma }[/math]小于1时，系统是亚临界的，活动随时间消亡。中间，当分支参数等于1的时候，系统是临界的，活动近似持续。实际上，活动将以幂律尾非常缓慢地消亡。底部，当分支参数大于1时，系统是超临界的，活动随时间增加。

明确预测神经活动雪崩的模型包括Herz和Hopfield（1995）的工作，该模型将神经网络中的混响与地震大小的幂律分布联系起来。同样值得注意的是Eurich、Hermann和Ernst（2002）的工作，他们预测来自全局耦合的非线性阈值元素网络的雪崩大小分布应该有一个[math]\displaystyle{ \alpha=1.5 }[/math]的指数。值得注意的是，这个指数与实验报告相吻合（Beggs和Plenz，2003）。

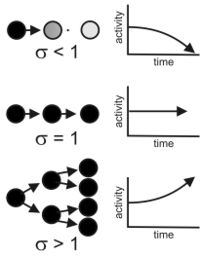
这里更详细地描述了一个分支过程模型（Harris, 1989; Beggs and Plenz, 2003; Haldeman and Beggs, 2005; reviewed in Vogels et al, 2005），因为它既能捕捉到雪崩大小的幂律分布，又能观察到数据中可重复的活动序列。在该模型中，在一个时间步长处于活动状态的处理单元将在下一个时间步长中平均产生[math]\displaystyle{ \sigma }[/math]处理单元中的活动。[math]\displaystyle{ \sigma }[/math]被称为分支参数，可以被认为是这个比率的预期值:

[math]\displaystyle{ \sigma=\frac{\mbox{后代}}{\mbox{祖先}} }[/math]

其中祖先是在时间步长t时活跃的处理单元的数量，后代是在时间步长t+1时活跃的处理单元的数量。如图所示，[math]\displaystyle{ \sigma }[/math]有三种一般状态。

图7：分支模型捕获数据的两个主要特征。 A，数据和模型的雪崩大小分布比较，显示出相当接近的对应关系。请注意，两者在对数空间都显示出直线部分，延伸到雪崩大小1-35。模型被调整到临界点，使分支参数[math]\displaystyle{ \sigma }[/math]等于1,没有其他自由参数。 B, 该模型产生的三个显著相似的雪崩家族。注意与前面显示的实际数据产生的雪崩系列的相似性。

在网络中的单个处理单元层面，分支参数[math]\displaystyle{ \sigma }[/math]由以下关系设定:

[math]\displaystyle{ \sigma_i=\sum_{j=1}^\mathit{N} \mathit{p_{ij}} }[/math]

其中[math]\displaystyle{ \sigma_i }[/math]是单元[math]\displaystyle{ i }[/math]激活的子代处理单元的预期数量，[math]\displaystyle{ N }[/math]是单元[math]\displaystyle{ i }[/math]连接的单元数量，[math]\displaystyle{ p_{ij} }[/math]是单元[math]\displaystyle{ i }[/math]的活动将传输到单元[math]\displaystyle{ j }[/math]的概率。由于一些传输概率大于其他传输概率，可能会出现优先传输路径，导致可重复的雪崩模式。如图所示，当[math]\displaystyle{ \sigma }[/math]被调整到临界点（[math]\displaystyle{ \sigma=1 }[/math]）时，该模型定性地捕捉到雪崩大小的幂律分布和重复雪崩（Haldeman and Beggs, 2005）。当模型适度调整到临界点以上（[math]\displaystyle{ \sigma\gt 1 }[/math]）或以下（[math]\displaystyle{ \sigma\lt 1 }[/math]）时，它不能产生雪崩大小的幂律分布。这一现象学模型没有明确说明分支过程背后的细胞或突触机制，该模型的许多预测仍待测试。

雪崩的影响

当一个可调谐系统运行在一个产生幂律分布的系统中时，它被说成是运行在临界点。严格地说，只有无限大的系统才能在临界点上运行，但这里的"临界"一词是用来描述有限系统的行为，如果它们被扩展到无限大，就会接近临界点。幂律雪崩大小分布对这四个领域的神经网络的信息处理有潜在的影响。

• 信息传输。当神经网络调整到临界点时，它们具有最佳的信息传输（Beggs和Plenz，2003；Bertschinger和Natschlager，2004；Kinouchi和Copelli，2006），因为在强信号传播和抗饱和之间存在平衡。
• 信息存储。当一个基于分支过程的递归网络被调整到临界点时，显著重复的雪崩模式的数量被最大化（Haldeman和Beggs，2005）。在临界点，存在着强连接和弱连接的混合，允许各种独立稳定的活动模式。
• 计算能力。通过改变尖峰网络模型中突触重量的变化，Bertschinger和Natschlager（Bertschinger和Natschlager 2004）能够产生显示出衰减、持续和扩张活动的网络。这些区域分别对应于亚临界、临界和超临界动力学。他们发现，在广泛的计算任务中，调谐到临界点的网络比调谐到亚临界或超临界动态的网络更有效。
• 稳定性。当一个循环分支网络模型被调整到临界点时，它产生的轨迹基本上是平行的，这意味着该网络处于稳定的边缘（Bertschinger和Natschlager，2004；Haldeman和Beggs，2005）。在这种情况下，轨迹仍然是稳定的，但可以通过较小的校正输入进行控制。

当网络在发生神经雪崩的临界点附近运行时，可以同时优化所有这些信息处理任务。

神经雪崩与其他系统的关系

事件大小的幂律分布通常出现在复杂的现象中，包括地震、相变、渗流、森林火灾、金融市场波动、生命游戏中的雪崩以及其他许多现象（Bak，1996）。在某些特定情况下，这种相似性似乎不仅仅是表面的。例如，地震模型结合了局部规则，其中一个地点的力被分配到最近的邻居，而没有消散。这种力守恒类似于上述临界分支模型中的概率守恒。这表明（Royer和Pare，2003）中报告的突触强度守恒可能是维持临界点附近网络的机制。在一个相关的想法中，模拟表明，当突触强度的总和徘徊在一个恒定值附近时，网络可以几乎保持临界（Hsu和Beggs，2006）。这可能是通过像突触缩放这样的机制来实现的（Turrigiano和Nelson，2000），并已经在实验中观察到了。最后，森林火灾模型中最近“燃烧”的区域是耐火的，而未燃烧的区域更容易着火。耐火性和兴奋性的这种平衡结合在一起，使系统保持在临界点附近。最近的神经雪崩模型（Levina、Herrmann和Geisel，2005）表明，短期突触抑制和促进也可能有助于推动神经元网络走向雪崩发生的临界点。因此，了解不同复杂系统中的幂律可以提出可能构成神经网络临界性基础的机制。

图8：在电容耦合霓虹灯的二维晶格中对雪崩产生的实验观察。

雪崩产生的一个简单电子模型由一个二维霓虹灯阵列组成，每个霓虹灯连接到一个朝向全局直流控制电压的电阻器，并电容耦合到其冯·诺依曼邻居。霓虹灯具有丰富的动态特性：随着外加电压的变化，"开 "和 "关 "阶段之间的转换同时具有明显的滞后性和随机性（Dance，1968）。该系统显示两个阶段，[math]\displaystyle{ I }[/math]和[math]\displaystyle{ II }[/math]，分别具有低和高事件率和时空顺序的特征：它们之间的过渡是强滞后的，因此明确为一阶。然而，在接近[math]\displaystyle{ I\rightarrow II }[/math]转换的脊柱点时，关键前驱体以雪崩的形式出现（图8），具有相同的表征神经活动的标度指数，即大小为[math]\displaystyle{ \alpha\approx3/2 }[/math]，持续时间为[math]\displaystyle{ \alpha\approx2 }[/math]（Minati等人，2016）。

外部链接和致谢

作者的个人网页

这项工作的撰写和图中的实验得到了美国国家科学基金会的资助和印第安纳大学的资助，约翰·贝格斯（John Beggs）的资助号为0343636。关于神经雪崩的最初工作是在迪特玛·普伦茨（Dietmar Plenz）的实验室完成的，由美国国立卫生研究院的院内研究项目资助。

参考文献

• Bak, P. (1996). How nature works: the science of self-organized criticality. New York, NY, USA, Copernicus.
• Bak P, Tang C, Wiesenfeld K (1987). Self-organized criticality: an explanation of the 1/f noise. Phys Rev Lett 59:381–384.
• Beggs, J. M. and D. Plenz (2003). Neuronal avalanches in neocortical circuits. J Neurosci 23(35): 11167-77.
• Beggs, J. M. and D. Plenz (2004). Neuronal avalanches are diverse and precise activity patterns that are stable for many hours in cortical slice cultures. J Neurosci 24(22): 5216-29.
• Bertschinger, N. and T. Natschlager (2004). "Real-time computation at the edge of chaos in recurrent neural networks." Neural Comput 16(7): 1413-36.
• Dance J. N. (1968). "Cold Cathode Tubes." Iliffe, London, UK.
• Eurich CW, Herrmann JM, Ernst UA (2002). Finite-size effects of avalanche dynamics. Phys Rev E Stat Nonlin Soft Matter Phys 66:066137.
• Haldeman, C, Beggs, JM (2005). Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys Rev Lett, 94: 058101.
• Harris TE (1989). The theory of branching processes. New York: Dover.
• Herz AV, Hopfield JJ (1995). Earthquake cycles and neural reverberations: collective oscillations in systems with pulse-coupled threshold elements. Phys Rev Lett 75:1222–1225.
• Hsu D, Beggs JM (2006). Neuronal avalanches and criticality: A dynamical model for homeostasis. Neurocomputing 69(1134-1136).
• Kinouchi O, Copelli M (2006). Optimal dynamic range of excitable networks at criticality. Nature Physics 2:348-351.
• Levina A, Herrmann JM, Geisel T (2005). Dynamical synapses give rise to a power law distribution of neuronal avalanches. Neural Information Processing Systems (NIPS) http://books.nips.cc/papers/files/nips18/NIPS2005_0646.pdf
• Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ (2001). Long-range temporal correlations and scaling behavior in human brain oscillations. J Neurosci 21:1370–1377.
• Lowen SB, Cash SS, Poo MM, Teich MC (1997). Quantal neurotransmitter secretion rate exhibits fractal behavior. J Neurosci 17:5666–5677.
• Minati, L; de Candia, A; Scarpetta, S. "Critical phenomena at a first-order phase transition in a lattice of glow lamps: Experimental findings and analogy to neural activity". Chaos. 26: 073103. doi:10.1063/1.4954879.
• Petermann T, Lebedev M, Nicolelis M, Plenz D (2006). Neuronal avalanches in vivo. Society for Neuroscience Abstracts.
• Royer S, Pare D (2003). Conservation of total synaptic weight through balanced synaptic depression and potentiation. Nature 422(6931):518-22.
• Segev R, Benveniste M, Hulata E, Cohen N, Palevski A, Kapon E, Shapira Y, Ben Jacob E (2002). Long term behavior of lithographically prepared in vitro neuronal networks. Phys Rev Lett 88:118102.
• Stewart CV, Plenz D (2006). Inverted-U profile of dopamine-NMDA-mediated spontaneous avalanche recurrence in superficial layers of rat prefrontal cortex. J Neurosci. 2006 Aug 2;26(31):8148-59.
• Teich MC, Heneghan C, Lowen SB, Ozaki T, Kaplan E (1997). Fractal character of the neural spike train in the visual system of the cat. J Opt Soc Am A Opt Image Sci Vis. 1997 Mar;14(3):529-46.
• Toib A, Lyakhov V, Marom S (1998). Interaction between duration of activity and time course of recovery from slow inactivation in mammalian brain Na_ channels. J Neurosci 18:1893–1903.
• Torre V (2006) Talk at NeuroIT conference in Genoa, Italy: http://www.neuroengineering.it/download/20.Torre.pdf
• Turrigiano GG, and Nelson SB (2000). Hebb and homeostasis in neuronal plasticity. Curr Opin Neurobiol 10:358-364.
• Vogels, T. P., K. Rajan and L. F. Abbott (2005). Neural network dynamics. Annu Rev Neurosci 28: 357-76.
• Worrell GA, Cranstoun SD, Echauz J, Litt B (2002). Evidence for self-organized criticality in human epileptic hippocampus. NeuroReport 13:2017–2021.

参见

复杂性, 复杂系统, 生命游戏, 自组织临界性