复杂性

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索


物理系统或动态过程的复杂性表达了组件参与有组织的结构化交互的程度。高度复杂的系统实现了有序和无序(规律性和随机性)的混合，并有很高的可能产生涌现现象。


各学科中的复杂性

尽管复杂性的概念在现代科学和社会中非常重要和普遍存在，但目前还没有一种普遍的、广泛接受的方法来衡量一个物理对象、系统或过程的复杂性。缺乏普遍的衡量标准，可能反映了我们对复杂系统的理解处于初始阶段，缺乏一个贯穿所有自然科学和社会科学的普遍的统一框架。虽然到目前为止，一般性的衡量标准仍然难以捉摸，但是，我们拥有许多适用于具体类型的系统或问题领域的复杂性衡量标准。尽管在定义和测量复杂性方面存在了各种不同的方法，但有一种信念仍然坚持认为所有复杂系统都有共同的特性，而且新的定义和度量正在不断地被一个由物理学家、生物学家、数学家、计算机科学家、经济学家和社会理论家组成的跨学科团体提出和检验。


本文从信息论的角度探讨复杂性问题。读者还可以从系统论的角度出发理解复杂性。


复杂性的一般特征

复杂性是秩序和混乱的混合体。在胡伯曼和霍格之后绘制（1986 年）。

复杂性的定量或分析学（analytic）定义往往不同意精确的表述，甚至不同意定义复杂性的正式框架。然而，有一种非正式的复杂性概念，它基于大多数(如果不是所有的话)复杂系统和过程所共有的一些要素。赫伯特 · 西蒙是最早讨论复杂系统的性质和结构的人之一(Simon，1981) ，他建议将复杂系统定义为那些“由大量具有许多相互作用的部分组成”的系统。西蒙接着指出，“在这样的系统中，整体不仅仅在[ ... ]的意义上大于各部分之和，考虑到各部分的性质及其相互作用的规律，推断整体的性质不是一件容易事。”


组分 许多复杂的系统可以分解成结构上不同的组成部分(组件、元素、单元) ，且它们可以作为个体发挥作用，产生某种形式的局部行为、活动或动态。复杂系统的组件本身可以分解为子组件，导致系统在多层次的组织中是复杂的，形成（不完全）可分解的组件层次结构。


交互 复杂系统的组成部分进行动态交互，导致这些组成部分跨空间和时间整合成一个有组织的整体。交互通常能调节组件的单个动作，从而通过中继全局上下文 relaying global context 改变其局部功能。在许多复杂系统中，组件子集之间的交互是通过某种形式的通信路径或连接进行的。这样的结构化交互通常是稀疏的，也就是说，所有可能的交互中只有一小部分是在系统中实现的。这些相互作用的具体模式对于确定系统作为一个整体如何运作至关重要。组件之间的某些相互作用可能很强，因为它们对于单个组件具有很大的效力。其他相互作用可能被认为是弱的，因为他们的影响范围或时间是有限的。无论是强相互作用还是弱相互作用，都能对整个系统产生重大影响。


涌现 系统中组件之间的相互作用往往产生不能被简单地归结为组件特性的现象、功能或效应。相反，这些功能是结构化交互的结果，是系统作为一个整体的属性。在许多情况下，即使对单个组件进行详细而全面的检查，也无法预测这些组件作为系统的一部分进行交互时能够发生的突发过程的范围。反过来，将一个集成的系统拆解成组件和相互作用通常会导致涌现过程的丢失。


总之，具有大量组件的、能够产生涌现现象的、结构化交互的系统可以称为复杂系统。对复杂系统得观察提出了许多挑战，因为观察者需要同时记录许多组件和交互的状态和状态转换。这种观测要求对状态的定义、状态空间和时间分辨率作出选择。怎样定义和度量系统的状态会影响到其他派生出来的度量方法，比如系统复杂性度量方法。


复杂性的度量

通过应用一个共同的度量标准，复杂性度量使得不同的系统可以相互比较。这对于结构上或功能上相关的系统尤其有意义。这些相关系统之间复杂性的差异可能揭示其组织的特征，从而促进我们对复杂性的理解。


一些复杂性度量是算法性质的，并试图确定最小描述长度（描述一个算法所需要的最短长度）。对于这些度量，复杂性仅适用于描述，而不适用于系统或流程本身。其他衡量复杂性的方法考虑到一个系统的时间演变，并且往往建立在统计信息理论的理论基础之上。


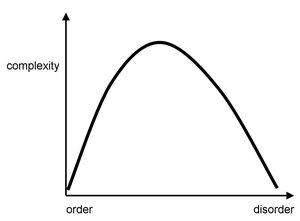
大多数现存的复杂性度量可以分为两大类。第一类(算法信息内容和逻辑深度)的复杂性度量试图捕捉系统或过程的随机性、信息内容或描述长度。随机过程具有最高的复杂性，因为它们最难以压缩。第二类(包括统计复杂性、物理复杂性和神经复杂性)将复杂性概念化为有别于随机性。在这里，复杂系统是那些拥有大量结构或信息的系统，通常跨越多个时间和空间尺度。在这一类度量中，高度复杂的系统处于高度有序(规则)和高度无序(随机)的系统之间。<figref>Complexity_figure1.jpg</figref> 展示了这些测量方法的示意图。然而，应该再次强调的是，目前并不存在一个普遍接受的、将复杂性和无序性联系起来的定量表达式。


复杂与随机

生成一个符号串的算法信息内容 Algorithmic Information Content 的定义(Kolmogorov，1965; Chaitin，1977)是生产这个符号串所需的最短计算机程序所包含的信息量。高度规则、周期性或单调的符号串可以由短小的程序生产，因此包含的信息很少，而完全随机的符号串需要一个和该符号串本身至少一样长的程序，因此产生高(最大)信息内容。举个例子，“0.333333...”所包含的算法信息内容很小，可以用“1/3”来生成；“3.14159265358974”次之，可以用求解圆周率的程序生成；“27648.73649325932”的算法信息内容最大，因为他是完全随机的（我随便敲键盘敲出来的），只能用它自己生产自己。算法信息内容(AIC)捕获了符号串的随机性，但似乎不适合应用于生物或神经系统。此外，算法信息内容虽然是一个精妙的概念，但在数学上是不可计算的，因此有诸多不便。


逻辑深度 Logical Depth(Bennett，1988)与 AIC 有关，并定义另一种计算复杂性：解决给定问题类所需的最小计算资源量(时间、内存)。作为逻辑深度的复杂性主要是指能够生成给定符号串或模式的最短程序的运行时间。与 AIC 类似，逻辑深度是对生成过程的度量，并不直接适用于实际存在的物理系统或动态过程。计算逻辑深度需要知道最短的计算机程序，因此受到与 AIC 相同的基本限制。


对于一个序列，如果已知其中的多少部分，就能预测剩下来的部分？这已知部分的序列中包含的信息，就是整个序列的有效度量复杂性 Effective Measure Complexity (Grassberger，1986)。有的书读了开头就能预测生下来的全部内容，那这本书的有效信息就只有开头所包含的信息量而已。有效度量复杂度可以捕捉在多个尺度范围内的序列中的结构，这与熵的扩展性有关(见下文)。


热力学深度 Thermodynamic Depth (Lloyd and Pagels，1988)将一个系统的熵与导致其系统状态的所有可能历史路径的数量联系起来。“深度”的系统是所有那些“难以建立”的系统，其最终状态蕴含着生成它的许多历史信息。热力学深度是逻辑深度的补充措施，侧重了一个系统的形成历史。虽然热力学深度的优点是可以通过经验来计算，但是如何定义系统状态是一个重要问题(Crutchfield 和 Shalizi，1999)。虽然它的目的是区分复杂系统和随机系统，但它的形式主义本质上抓住了生成过程所产生的随机性，而不区分规则系统和随机系统。


作为结构和信息的复杂性

在结构基础上量化复杂性的一个简单方法是计算一个系统中的组件和/或交互的数量。对生物进化过程中结构部分的数量(McShea，1996)和功能行为的研究表明，这些指标会随着时间的推移而增加，这一发现有助于持续辩论复杂性是否是自然选择的结果。然而，数量本身可能只是复杂性的一个指标，而不完全是复杂性的指标。大型和高度耦合的系统可能并不比那些较小和耦合较少的系统复杂。例如，一个完全连接的非常大的系统可以用一种紧凑的方式来描述，并且可能会产生统一的行为，而一个较小但是更多异质的系统的描述可能不那么可压缩，其行为可能更加不同。相同节点数量下，无标度网络往往比全连接网络更复杂。


有效复杂性 Effective complexity (Gell-Mann，1995)度量了系统规律性的最小描述长度。这种测量方法与 AIC 有关，但它试图区分常规特征和随机或偶然特征，因此属于旨在获取系统包含多少结构的复杂性测量方法的范畴。对于任何给定的经验系统来说，区分开规则特征和随机特征都是困难的，而且它可能取决于外部观察者提供的标准。


物理复杂度 Physical complexity (Adami 和 Cerf，2000)与有效复杂性有关，其目的是估计任何符号序列的复杂性，这些符号是关于物理世界或环境的。因此，这一措施在应用于生物系统时特别有用。给定一个符号序列(比如基因组)，和一些使得该序列具有意义的环境（比如生态位）的描述，它们之间共有的算法复杂度（AIC），就是物理复杂性。由于算法复杂度是不可计算的，物理复杂度也不能。然而，一组序列(例如整个生物体的基因组集合)的平均物理复杂性可以用序列(基因组)集合与其环境(生态学)之间的相互信息来近似。在数字生态学(Adami，2002)中进行的实验表明，自我复制的基因组与其环境之间的互信息随着进化时间的增加而增加。物理复杂度也被用来估计生物分子的复杂性。一组 RNA 分子的结构和功能复杂性与物理复杂性呈正相关(Carothers 等人，2004) ，这表明进化的分子结构的功能与它们编码的信息量之间可能存在联系。


电影帧来自神经动力学的演示模型，由1600个自发活跃的威森-考恩神经质量单元组成，这些单元排列在球体上，并辅之以兴奋连接。 显示三个案例：稀疏耦合（仅限本地连接）、均匀耦合（仅限全球连接）以及本地和全球连接的混合（形成小世界网络）。 神经复杂性（托尼等人，1994年;斯波恩斯等人，2000年）是高只为最后一个案件。


统计复杂度 Statistical Complexity(Crutchfield and Young，1989)是一个更广泛的、被称为计算力学 Computational Mechanics的理论框架的组成部分，并可以直接从经验数据估算。为了计算统计复杂度，时间序列中的每个点根据某种划分方案映射到对应的符号，使原始数据成为一个连续的符号流。然后，符号序列按照以下规则聚类成因果状态: 如果任何未来符号的条件概率对于这两个历史是相同的，那么两个符号序列(即动力学的历史)就属于相同的因果状态。换句话说，如果两个符号序列预测了同一个未来的动力学分布，那么可以认为这两个符号序列是相同的。一旦确定了这些因果状态，就可以从数据中提取因果状态之间的转换概率，并计算出所有因果状态的长期概率分布。统计复杂度被定义为因果状态上这种分布的香农熵。对于逻辑斯谛映射、元胞自动机和许多基本的马尔可夫过程等抽象系统，统计复杂性可以通过解析方法计算出来。


预测信息 Predictive Information (Bialek 等，2001) ，虽然本身不是一个复杂性度量，但可以用来根据熵的可扩展性原理将系统分成不同的复杂性类别。例如，可扩展性表现在由越来越多的同质独立随机变量组成的系统中。这类系统的香农熵将随其大小线性增长。熵随系统大小的线性增长称为扩展性。然而，复杂系统的组成元素通常是异质的和相互依赖的。因此当随机变量数量的增长，熵并不总是线性增长的。一个给定系统偏离扩展性的方式也可以用来描述其复杂性。


神经复杂性 Neural Complexity(Tononi 等，1994) ，与系统的延伸性相关，可以应用于任何经验系统，包括大脑。神经复杂度中的一个重要概念是集成度 Integration(也称为多信息) ，这是互信息的多元扩展，用于估计任意大系统中的统计结构的总量。集成度被定义为组成部分的个体熵之和与系统作为一个整体的联合熵之差。集成度在多个空间尺度上的分布表明了系统的复杂性。考虑以下三种情况： (1)具有统计独立成分的系统会呈现全局无序或随机动态。它的联合熵将正好等于组成熵之和，系统的集成度将为零，无论哪个空间尺度的系统被检查。 (2)各组分之间的统计相关性将导致系统的联合熵相对于个体熵的收缩，从而导致正的集成度。如果一个系统的组成部分是高度耦合的，并且表现出统计依赖性以及同质动力学(即所有组成部分的行为完全相同) ，那么该系统的多个空间尺度上的集成估计平均遵循线性分布。 (3)如果统计依赖关系是非同质的(例如涉及组件、模块或层次模式的分组) ，则集成的分布将偏离线性。偏差的总量是系统的复杂性。随机系统的复杂度为零，而齐次耦合系统的复杂度非常低。具有丰富结构和动态行为的系统具有很高的复杂性。


应用于神经动力学，托诺尼等人(1994年)定义的复杂性被发现与神经连接的特定模式有关，例如小世界网络所表现出来的属性(Sporns 等，2000)。这种复杂性度量的和在此基础上提出来的各种度量已经解决了系统与环境的匹配以及它们的简并性问题。


复杂网络

传统上，复杂系统的分析一直使用非线性动力学和统计信息理论的工具。最近，复杂网络的分析学框架引发了对不同科学领域复杂系统之间共性和差异的重新评估(Amaral 和 Ottino，2004)。一个关键的洞察是网络拓扑——交互的图结构，通过引导信息流，创造组件之间的一致性模式，以及塑造宏观系统状态的涌现，对系统的动力学施加了重要的约束。复杂性对网络拓扑的变化高度敏感。因此，连接模式或强度的改变可以作为复杂性的调节器。网络结构与动力学之间的联系是近期复杂性研究中最有前途的领域之一。


为什么是复杂性？

到底为什么复杂性会存在，特别是在生物系统中？这个问题的确切答案仍然难以捉摸。一种观点是基于生物系统所面临的进化需求。生物结构和生物体的进化成功取决于它们捕获环境信息的能力，无论是分子层面的还是生态层面的。生物的复杂性可能就会涌现，作为进化压力作用于生物体结构的结果。


另一条线索可能在复杂性和网络结构之间的联系中找到。复杂性在大规模集成了不同组件的系统中显得非常突出。这些系统变得更加复杂，因为它们更有效地整合更多的信息，也就是说，它们更有能力既适应专门的组件，也适应将这些组件绑定为一个连贯整体的结构化交互作用。因此，调和部分和整体，复杂性可能是自然界种基本辩证法的表现。


引用

  • Adami, C. (2002) What is complexity? BioEssays 24, 1085-1094.
  • Adami, C., Cerf, N.J. (2000) Physical complexity of symbolic sequences. Physica D 137, 62-69.
  • Amaral, L.A.N., Ottino, J.M. (2004) Complex networks. Eur. Phys. J. B 38, 147-162.
  • Bennett, C.H. (1988) Logical depth and physical complexity. In: R. Herken (ed.): The Universal Turing Machine. A Half-Century Survey. Pp. 227-257, Oxford: Oxford University Press.
  • Bialek, W., Nemenman, I., Tishby, N. (2001) Predictability, complexity, and learning. Neural Computation 13, 2409-2463.
  • Carothers, J.M., Oestreich, S.C., Davis, J.H., and Szostak, J.W. (2004) Informational complexity and functional activity of RNA structures. J. Am. Chem. Soc. 126, 5130–5137.
  • Chaitin, G.J. (1977) Algorithmic information theory. IBM Journal of Research and Development 21, 350-359. [1]
  • Crutchfield, J.P., Young, K. (1989) Inferring statistical complexity. Phys. Rev. Lett. 63, 105-109.
  • Crutchfield, J.P., Shalizi, C.R. (1999) Thermodynamic depth of causal states: Objective complexity via minimal representations. Phys. Rev. E 59, 275-283.
  • Gell-Mann, M. (1995) What is complexity? Complexity 1, 16-19.
  • Grassberger, P. (1986) Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 25, 907-928.
  • Huberman, B.A., Hogg, T. (1986) Complexity and adaptation. Physica D 22, 376-384.
  • Kolmogorov, A. N. (1965) Three approaches to the quantitative definition of information. Problems of Information Transmission 1, 1-17.
  • Lloyd, S., Pagels, H. (1988) Complexity as thermodynamic depth. Annals of Physics 188, 186-213.
  • McShea, D.W. (1995) Metazoan complexity and evolution: Is there a trend? Evolution 50, 477-492.
  • Simon, H.A. (1981) The Sciences of the Artificial. MIT Press: Cambridge.
  • Sporns, O., Tononi, G., Edelman, G.M. (2000) Theoretical neuroanatomy: Relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb. Cortex 10, 127-141.
  • Tononi, G., Sporns, O., Edelman, G.M. (1994) A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. U.S.A. 91, 5033-5037.


Scholarpedia内部引用

  • Marcus Hutter (2007) Algorithmic information theory. Scholarpedia, 2(3):2519.
  • Valentino Braitenberg (2007) Brain. Scholarpedia, 2(11):2918.
  • Gregoire Nicolis and Catherine Rouvas-Nicolis (2007) Complex systems. Scholarpedia, 2(11):1473.
  • James Meiss (2007) Dynamical systems. Scholarpedia, 2(2):1629.
  • Tomasz Downarowicz (2007) Entropy. Scholarpedia, 2(11):3901.
  • Arkady Pikovsky and Michael Rosenblum (2007) Synchronization. Scholarpedia, 2(12):1459.


外部链接


编者推荐

集智学园

复杂经济学系列读书会

复杂性科学的思想和方法可以为经济学研究再开一扇通向未来之门。本次读书会以科研交流为主，希望以此普及复杂经济学思想，促进复杂经济学教育，推进复杂经济学研究。


本课程中，我们邀请了统计物理交叉学科领域五位杰出学者分享他们在复杂网络和系统领域最新的研究成果。JPhys Complexity 主编 Ginestra Bianconi 也将分享在多学科交叉融合的国际大势之下，期刊将如何顺应科学研究的趋势，为有效解决万物互联带来的更加复杂、系统的科学问题和社会问题提供新的洞见。


本系列课程为北京师范大学系统科学学院陈晓松老师开设的《复杂性与临界现象》课程回放。



本条目由Ricky审校，糖糖、不是海绵宝宝编辑，如有问题，欢迎在讨论页面进行讨论。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=复杂性&oldid=26994”