WS小世界模型

小世界模型（Watts–Strogatz model）由邓肯·瓦茨 Duncan J. Watts和史蒂夫·斯托加茨 Steven Strogatz在1998年两人联合发表于《Nature》的论文中提出 。Watts和Strogatz随后提出了一种新的图模型（即现在的Watts-Strogatz模型）。

模型基本原理

对随机图的正式研究可追溯至 保尔·厄多斯 Paul Erdős和阿尔弗烈德·瑞利 Alfréd Rényi的工作 。他们所考虑的图，也就是现在所谓的经典图或ER随机图模型，给许多应用提供了简单而强有力的模型。

但ER图并不具有我们观察到的许多实际网络所拥有的两个重要属性：

1. 不能生成局部集聚 local clustering 和三元闭合 triadic closures(网络有三元闭合、三元闭包等释义）。相反，因为图中两个节点有恒定、随机且独立的概率彼此相连，ER随机图模型的集聚系数较低。
2. 不能解释中心节点 hub 的构成。在形式上，ER随机图模型的度分布收敛于泊松分布 Poisson distribution ，而不是我们在现实世界中观测到的、无标度网络 scale-free networks 的幂律分布 power law

WS小世界模型是针对于第一条局限性来设计的最简可能模型。它在解释了集聚的同时保持了ER模型较短的平均节点间距离，这是通过在近似ER图的随机化结构和正则环点阵 regular ring lattice中进行内插得到的。因而，该模型至少能够部分解释许多网络中的“小世界”现象 "small-world" phenomena，比如电网、秀丽隐杆线虫 C. elegans的神经网络、电影演员的社交网络、以及芽殖酵母脂肪代谢的信息交流 。

算法

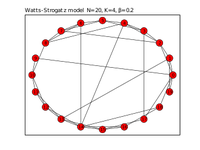
假设所期望的节点数为[math]\displaystyle{ N }[/math]，平均度为[math]\displaystyle{ K }[/math]（假定[math]\displaystyle{ K }[/math]为偶数）和一个特殊的参数[math]\displaystyle{ \beta }[/math] ，满足[math]\displaystyle{ 0\leq \beta \leq 1 }[/math]，且[math]\displaystyle{ N\gg K\gg lnN\gg 1 }[/math]。

该模型以下述方式构建了一个具有[math]\displaystyle{ N }[/math]个节点，[math]\displaystyle{ \frac{NK}{2} }[/math]条边的无向图：

1. 构建一个正则环点阵。该图有[math]\displaystyle{ N }[/math]个节点，每个节点和[math]\displaystyle{ K }[/math]个相邻的节点相连，其中每一侧有[math]\displaystyle{ K/2 }[/math]个。即是，若每个节点用[math]\displaystyle{ n_{0},...,n_{N-1} }[/math]标示，当且仅当[math]\displaystyle{ 0\lt \left | i-j \right |\mod(N-1-\frac{K}{2})\leq \frac{K}{2} }[/math]时，存在边[math]\displaystyle{ (n_{i},n_{j}) }[/math]。
2. 对于每个节点[math]\displaystyle{ n_{i}=n_{0},...,n_{N-1} }[/math]，选出其与最右侧第[math]\displaystyle{ K/2 }[/math]相邻节点之间的边，即满足[math]\displaystyle{ n_{i} \lt n_{j} \leq n_{i} + K/2 }[/math]的所有边 [math]\displaystyle{ (n_{i},n_{j}\mod N) }[/math] ，以概率[math]\displaystyle{ \beta }[/math]将其重新连接。重新连接的过程是把边 [math]\displaystyle{ (n_{i},n_{j}\mod N) }[/math] 替换为边 [math]\displaystyle{ (n_{i},n_{k}) }[/math] ，其中[math]\displaystyle{ k }[/math]以一致的随机性从所有可能的节点选出，并且避免出现自回路[math]\displaystyle{ (k\neq i) }[/math]和重复连接（边 [math]\displaystyle{ (n_{i},n_{{k}'}) }[/math] ，其中[math]\displaystyle{ {k}'=k }[/math]，在该算法中不会出现）的情况。

特性

该模型基础的点阵图结构产生了局部集聚的网络，而随机的重新连接则大大减少了平均节点间距离。其算法引入了大约[math]\displaystyle{ \beta \tfrac{NK}{2} }[/math]条非点阵边。改变[math]\displaystyle{ \beta }[/math]的值可以在正则环点阵（[math]\displaystyle{ \beta =0 }[/math]）和接近ER随机图的结构[math]\displaystyle{ (\beta = }[/math][math]\displaystyle{ 1 }[/math]，[math]\displaystyle{ G }[/math][math]\displaystyle{ (N,p) }[/math]满足[math]\displaystyle{ p=\frac {K}{N-1}) }[/math]间进行内插。由于每一个节点都与至少[math]\displaystyle{ K/2 }[/math]个其他节点相连，该模型并没符合真实的ER模型。

我们感兴趣的三个特性是平均节点间距离、集聚系数和度分布。

Watts–Strogatz 小世界模型，由igraph生成，Cytoscape 2.5进行可视化，100个节点

Watts_strogatz图

平均节点间距离

• 对于环形点阵，平均节点间距离是[math]\displaystyle{ \ell(0)=N/2K\gg 1 }[/math]，且随系统规模线性变化；

• 对于极限情况[math]\displaystyle{ (\beta \rightarrow 1) }[/math]，该图趋近于随机图，平均节点间距离[math]\displaystyle{ \ell(1)=\frac{lnN}{lnK} }[/math]，但实际上不收敛于此；

• 在区间[math]\displaystyle{ (0\lt \beta \lt 1) }[/math]内，平均节点间距离随着[math]\displaystyle{ \beta }[/math]的增大迅速下降，并很快接近于其极限值。

集聚系数

• 对于环形点阵，集聚系数 为[math]\displaystyle{ C(0)=\frac{3(K-2)}{4(K-1)} }[/math]，因此随着K的增大趋向于[math]\displaystyle{ 3/4 }[/math]，且与系统规模无关；
• 对于[math]\displaystyle{ \beta \rightarrow 1 }[/math]的极限情况，集聚系数与经典随机图同阶，[math]\displaystyle{ C=\frac{K}{N-1} }[/math]，与系统规模成反比；区间内的集聚系数则十分接近于正则环点阵的系数值，只有在[math]\displaystyle{ \beta }[/math]相对较大时才会下降，这就导致了在一定区间范围内平均节点间距离下降迅速，而集聚系数保持相对恒定的情形，也就解释了“小世界”现象。
• 如果我们用巴拉特 Barrat和魏格特 Weigt的方法，即是用一个节点的相邻节点之间的平均边数和这些相邻节点之间可能的平均边数之商来定义集聚系数[math]\displaystyle{ C'(\beta) }[/math]，或者说:

[math]\displaystyle{ C'(\beta)=\frac{3\times \text{number of triangles}}{\text{number of connected triples}} }[/math]

可得出[math]\displaystyle{ C'(\beta)\sim C(0)(1-\beta)^{3} }[/math]

度分布

• 正则环点阵的度分布即以K为中心的狄拉克[math]\displaystyle{ \delta }[/math]函数，在[math]\displaystyle{ 0\lt \beta \lt 1 }[/math]内的度分布可记为：

[math]\displaystyle{ P(k) = \sum_{n=0}^{f(k,K)} {{K/2}\choose{n}} (1-\beta)^n \beta^{K/2-n} \frac{(\beta K/2)^{k-K/2-n}}{(k-K/2-n)!} e^{-\beta K/2} }[/math]

[math]\displaystyle{ k_{i} }[/math]是第[math]\displaystyle{ i }[/math]个节点的边数或称为度。这里[math]\displaystyle{ k\geq K/2 }[/math]，[math]\displaystyle{ f(k,K)=min(k-K/2,K/2) }[/math]。

• 度分布的形状类似于随机图，在[math]\displaystyle{ k }[/math][math]\displaystyle{ = }[/math][math]\displaystyle{ K }[/math]处取得明显峰值，对于较大的[math]\displaystyle{ \left | k-K\right | }[/math]呈指数衰减。

• 网络的拓扑相对而言是齐次的，也即所有的节点都有相同的度。

参见

• 小世界网络
• ER随机图模型
• BA网络模型
• 社交网络

编者推荐

书籍推荐

《网络科学导论》封面

网络科学导论第七章小世界网络模型

《网络科学导论》由汪小帆，李翔，陈关荣联袂编著，致力于系统地介绍网络科学的基本概念、思想和方法，使得具有高等数学基础的读者都能够看懂，并具备把网络科学方法用于实际网络分析的能力。为此，本书没有过多地陷入数学和物理推导，而是更为关注网络科学的思维习惯和研究方式。

课程推荐

复杂网络2020

本课程是对复杂性科学的一个概述，包含10个章节，每节都会涵盖复杂系统的一个主要概念。

集智相关文章

从复杂网络小世界、无标度、高聚类特性看新型冠状病毒肺炎

该文章基于复杂网络最基本的三大特点——小世界、无标度、高聚类，来分析新型冠状病毒肺炎这一场突如其来的灾难。

---

本中文词条由用户Iceblaze9527参与编译，flynn审校，张江总审校，乐多多、薄荷编辑，欢迎在讨论页面留言。

本词条内容源自公开资料，遵守 CC3.0协议。