“因果涌现”的版本间的差异
(→模型约简) |
|||
| 第274行: | 第274行: | ||
在复杂系统中,由于微观状态往往存在噪音,需要将微观状态进行粗粒化得到噪音更小的宏观状态,使得宏观动力学的因果性更强。同样对于因果模型也一样,由于原始模型过于复杂,或者计算资源受限,所以往往需要得到更加抽象的因果模型,并且保证抽象的模型尽可能保持原始模型的因果机制,因果模型抽象讨论的也是因果关系与模型抽象(可以看成粗粒化过程)之间的相互作用<ref>S. Beckers, F. Eberhardt, J. Y. Halpern, Approximate causal abstractions, in: Uncertainty in artificial intelligence, PMLR, 2020, pp. 606–615.</ref>。因此,因果涌现识别与因果模型抽象有很多相似之处,可以把原始的因果机制理解为微观动力学,抽象出来的机制理解为宏观动力学。在神经信息压缩框架中(NIS),对粗粒化策略和宏观动力学进行了限制,要求宏观动力学的微观预测误差要足够小以排除平凡解。这个要求也类似于因果模型抽象中希望抽象后的因果模型与原始模型的距离要尽可能相近。但是两者也存在一些不同:1)因果涌现中是对状态或数据进行粗粒化,而因果模型抽象是对模型进行操作;2)因果模型抽象中考虑混肴因子,然而却被因果涌现的讨论忽略。 | 在复杂系统中,由于微观状态往往存在噪音,需要将微观状态进行粗粒化得到噪音更小的宏观状态,使得宏观动力学的因果性更强。同样对于因果模型也一样,由于原始模型过于复杂,或者计算资源受限,所以往往需要得到更加抽象的因果模型,并且保证抽象的模型尽可能保持原始模型的因果机制,因果模型抽象讨论的也是因果关系与模型抽象(可以看成粗粒化过程)之间的相互作用<ref>S. Beckers, F. Eberhardt, J. Y. Halpern, Approximate causal abstractions, in: Uncertainty in artificial intelligence, PMLR, 2020, pp. 606–615.</ref>。因此,因果涌现识别与因果模型抽象有很多相似之处,可以把原始的因果机制理解为微观动力学,抽象出来的机制理解为宏观动力学。在神经信息压缩框架中(NIS),对粗粒化策略和宏观动力学进行了限制,要求宏观动力学的微观预测误差要足够小以排除平凡解。这个要求也类似于因果模型抽象中希望抽象后的因果模型与原始模型的距离要尽可能相近。但是两者也存在一些不同:1)因果涌现中是对状态或数据进行粗粒化,而因果模型抽象是对模型进行操作;2)因果模型抽象中考虑混肴因子,然而却被因果涌现的讨论忽略。 | ||
===模型约简=== | ===模型约简=== | ||
| − | + | 模型约简,就是要将高维的复杂系统动力学模型进行化简、降维,用低维的动力学来描述动力系统的演化规律,这一过程其实就是因果涌现研究中的粗粒化过程。将对大尺度动力系统的近似方法主要有两大类,即基于奇异值分解的近似方法和基于Krylov的近似方法。前者基于奇异值分解,后者基于矩匹配。虽然前者具有许多理想的性质,包括误差界,但它不能应用于高复杂度的系统。另一方面,后者的优势在于它可以迭代实现,因此适用于高复杂度系统。将这两个族的最佳属性相结合的努力导致了第三类近似方法,称为SVD/Krylov。两种方法都是基于粗粒化前后输出函数的误差损失函数。 | |
所谓的大尺度动力学一般情况下,如果时间是连续的,就可以表示为 | 所谓的大尺度动力学一般情况下,如果时间是连续的,就可以表示为 | ||
| 第286行: | 第286行: | ||
<math>x_{t+1}=f(x_t,u_t), z_t=g(x_t,u_t) </math> | <math>x_{t+1}=f(x_t,u_t), z_t=g(x_t,u_t) </math> | ||
| − | 对大尺度动力学进行约简,需要先对变量进行线性映射<math>y=Wx, W\in\mathcal{R}^{k\times n}, k<n </math> | + | 对大尺度动力学进行约简,需要先对变量进行线性映射<math>y=Wx, W\in\mathcal{R}^{k\times n}, k<n </math>。这样就可以对我们动力系统模型进行简化,得到约简后的系统 |
| + | |||
| + | <math>\frac{dy}{dt}=Wf(Vx,u), \hat{z}=g(Vx,u) </math> | ||
| + | |||
| + | 或 | ||
| + | |||
| + | <math>y_{t+1}=Wf(Vy_t,u_t), \hat{z}_t=g(Vx_t,u_t) </math> | ||
| + | |||
| + | 其中<math>V\in\mathcal{R}^{n\times k}, WV=I_n </math>,寻找合适的W也是以往研究的关键。 | ||
===动力学模式分解=== | ===动力学模式分解=== | ||
2024年6月30日 (日) 19:07的版本
因果涌现(causal emergence)是指动力系统中的一类特殊的涌现现象,即系统在宏观尺度会展现出更强的因果特性。特别的,对于一类马尔可夫动力学系统来说,在对其状态空间进行适当的粗粒化以后,所形成的宏观动力学会展现出比微观更强的因果特性,那么称该系统发生了因果涌现[1][2]。马尔可夫动力学系统是指系统在某一时刻的状态仅仅依赖于系统上一时刻所处的状态,而与更早的状态无关。这里的粗粒化是指对系统的状态空间进行约简的一种方法,它往往可以表示为一个具有降维特征的函数映射。所谓的宏观动力学是指在被粗粒化后的新状态空间上的随附的(supervenes)动力学,它完全取决于微观的动力学和粗粒化方式。
历史
涌现一直是复杂系统中的一个重要特性和研究对象,是许多关于复杂性本质以及宏微观组织之间关系讨论的中心概念[3][4]。涌现可以简单理解为整体大于部分之和,即整体上展现出构成它的个体所不具备的新特性[5]。尽管在各个领域都被指出存在涌现的现象,如鸟类的群体行为,大脑中的意识形成,以及大语言模型的涌现能力,但目前还没有对这一现象的统一理解。以往对涌现有很多定性的研究,如 Bedau et al对涌现进行了分类,可以将涌现分为名义涌现、弱涌现与强涌现。名义涌现可以理解为能被宏观层级的模式或过程所拥有,但不能被其微观层级的组件所拥有的属性。弱涌现是指宏观层面的属性或过程是通过单个组件之间以复杂的方式相互作用产生的,由于计算不可约性的原理,它们不能轻易地简化为微观层面的属性。对于弱涌现来说,其模式产生的原因可能来自微观和宏观两个层面。因此,涌现的因果关系可能与微观因果关系并存。而对于强涌现来说存在很多的争论,它指的是宏观层面的属性,原则上不能简化为微观层面的属性,包括个体之间的相互作用。此外,Jochen Fromm进一步将强涌现解释为向下因果的因果效应。考虑一个包含三个不同尺度的系统:微观、介观和宏观。向下因果关系是指从宏观层面向介观层面或从介观层面向微观层面的因果力。然而,关于向下因果关系本身的概念存在许多争议。
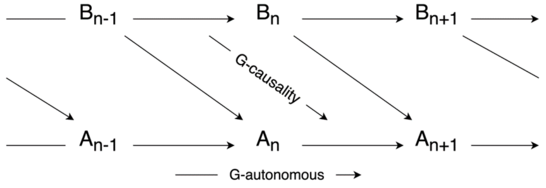
虽然有了涌现的定性分类,然而却无法定量的刻画涌现的发生。早期已经有一些相关的工作尝试对涌现进行定量的分析。例如,Crutchfield等[6]提出的计算力学理论考虑了因果状态,该方法是对状态空间的划分。而Seth等人则提出了G-emergence理论[7]利用格兰杰因果关系来量化涌现。具体来说,计算力学理论试图用定量的框架来表述涌现的因果关系,希望从一个随机过程的观测中构造一个最小的因果模型,从而来产生观测的时间序列[6]。其中随机过程可以用[math]\displaystyle{ \overleftrightarrow{s} }[/math]表示,基于时间[math]\displaystyle{ t }[/math]可以将随机过程分为两个部分,时间前和时间后的过程,[math]\displaystyle{ \overleftarrow{s_t} }[/math]和[math]\displaystyle{ \overrightarrow{s_t} }[/math],当这个过程是平稳过程时,可以去掉时间。因此,可以将所有可能的历史过程[math]\displaystyle{ \overleftarrow{s_t} }[/math]形成的集合记作[math]\displaystyle{ \overleftarrow{S} }[/math],所有未来的过程形成的集合记作[math]\displaystyle{ \overrightarrow{S} }[/math]。可以将[math]\displaystyle{ \overleftarrow{S} }[/math]分解为相互排斥又联合全面的子集,形成的集合记为[math]\displaystyle{ \mathcal{R} }[/math],[math]\displaystyle{ R \in \mathcal{R} }[/math]中的任意子集可以看作是一个状态,定义一个分解函数[math]\displaystyle{ \eta:S→\mathcal{R} }[/math]。此外,定义了因果等价的概念,如果[math]\displaystyle{ P\left ( \overrightarrow{s}|\overleftarrow{s}\right )=P\left ( \overrightarrow{s}|{\overleftarrow{s}}'\right ) }[/math],则[math]\displaystyle{ \overleftarrow{s} }[/math]和[math]\displaystyle{ {\overleftarrow{s}}' }[/math](表示[math]\displaystyle{ \overleftarrow{s} }[/math]的子集)是因果等价的。将历史[math]\displaystyle{ \overleftarrow{s_t} }[/math]的所有因果状态定义为[math]\displaystyle{ \epsilon \left ( \overleftarrow{s} \right ) }[/math],将两个因果状态[math]\displaystyle{ S_i }[/math]和[math]\displaystyle{ S_j }[/math]之间的因果转移概率记为[math]\displaystyle{ T_{ij}^{\left ( s \right )} }[/math],一个随机过程的[math]\displaystyle{ \epsilon-machine }[/math]被定义为有序对[math]\displaystyle{ \left \{ \epsilon,T \right \} }[/math],是一种模式发现机器,其中[math]\displaystyle{ \epsilon }[/math]是因果状态函数, [math]\displaystyle{ T }[/math]是通过[math]\displaystyle{ \epsilon }[/math]定义的状态转移矩阵的集合。通过证明[math]\displaystyle{ \epsilon-machine }[/math]具有最大程度的预测性和最小程度的随机性这两个重要特性验证了它在某种意义上是最优的。但是方法没有给出涌现的明确定义和定量理论,随后一些研究人员进一步推进了计算力学的发展,Shalizi等[8]在自己的工作中讨论计算力学与涌现的关系,同时在另一个工作中,Shalizi等[9]还将计算力学应用于元胞自动机,并且在更高的描述水平上发现涌现的“粒子”。而G-emergence理论是Seth于2008年提出的最早对涌现进行定量量化的研究之一[7],基本思想是用非线性格兰杰因果来量化复杂系统中的弱涌现。具体来说,使用二元自回归模型进行预测,当只存在两个变量A和B时,自回归模型存在两个等式,每个等式对应其中一个变量每个时刻值的构成,每个变量的当前时刻值都是由自身变量和另外一个变量在滞后时间范围内的变量以及残差项构成,残差可以理解为预测误差,残差可以用来衡量格兰杰因果(G-causality)的因果效应程度。B作为A的格兰杰因(G-cause)的程度通过两个残差方差之比的对数来计算,其中一个是在省略B的所有项时A的自回归模型的残差,另一个是全预测模型的残差。此外,作者还定义了G-autonomous,表示一个时间序列的过去值可以帮助预测自身的未来值。G-autonomous的程度可以用类似量化格兰因果的方法来测量。
基于上述G-causality中的两个基本概念,可以来判断涌现的发生(这里是基于格兰杰因果的涌现的衡量,记作G-emergence)。如果把A理解为宏观变量,B理解为微观变量。发生涌现的条件包含两个:1)A是关于B的G-autonomous;2)B是A的G-cause。其中G-emergence的程度是通过A的G-autonomous的程度与B的平均G-cause的程度的乘积来计算。Seth提出的G-emergence理论首次尝试使用因果关系来量化涌现现象,然而,作者使用的因果关系是格兰杰因果,这不是一个严格的因果关系,同时结果也取决于所使用的回归方法。此外,方法的度量指标是根据变量而不是动力学定义的,这意味着结果会依赖于变量的选择。
此外,也存在一些其他的涌现定量理论,主要有两种方法被广泛讨论。一种是从无序到有序的过程来理解涌现,Moez Mnif和Christian meller-schloer使用香农熵来度量有序和无序。在自组织过程中,当秩序增加时就会出现涌现,通过测量初始状态和最终状态之间的香农熵的差异来计算秩序的增加,然而该方法存在一些缺陷:依赖于抽象的观察水平以及系统初始条件的选择,为了克服这两种困难,作者提出了一种与最大熵分布相比的度量香农熵的相对水平的方法。受Moez mif和Christian meller-schloer工作的启发,参考文献建议使用两个概率分布之间的散度能更好地量化涌现。他们将涌现理解为在所观察到的样本基础上的一种意想不到的或不可预测的分布变化。但该方法存在计算量大、估计精度低等缺点。为了解决这些问题,文献[84]进一步提出了一种使用高斯混合模型估计密度的近似方法,并引入马氏距离来表征数据与高斯分量之间的差异,从而得到了更好的结果。此外,Holzer和de Meer等人提出了另一种基于Shannon熵的涌现测量方法。他们认为一个复杂的系统是一个自组织的过程,在这个过程中,不同的个体通过通信相互作用。然后,可以根据代理之间所有通信的香农熵度量与作为单独源的每次通信的香农熵总和之间的比率来测量涌现。另一种是从“整体大于部分之和”的角度来理解涌现,该方法定义来自交互规则和代理状态的涌现,而不是整个系统的总体统计度量。具体地说,这个度量由两个相互相减的项组成。第一项描述了整个系统的集体状态,而第二项代表了所有组成部分的单个状态的总和,该度量强调涌现产生于系统的相互作用和集体行为。
上述的一些定量量化涌现的方法往往没有考虑因果关系,最接近的也只是使用格兰杰因果不是真正的因果。随着近年来因果科学理论得到了进一步的发展,使得可以用数学框架来量化因果,因果描述的是一个动力学过程的因果效应[10][11][12]。Judea Pearl利用概率图形模型(如贝叶斯网络、因果图和结构因果模型)来描述因果相互作用。Pearl用不同的模型来区分并量化了三个层次的因果关系。第一级是关联,即变量之间的相关性,可以使用贝叶斯网络来建模。第二层是干预,可以用因果图模型来表征。因果图和贝叶斯网络之间的区别在于,前者引入了干预操作。最后一个层次是反事实,它可以用结构因果模型来量化。结构因果模型的显著特征是,因果图中的所有相互作用都可以用一组确定性函数来描述,这些函数涉及输入变量和未知成分,从而引入不确定性。另一个因果推理的定量框架是Donald B Rubin的“潜在结果”理论,该理论在反事实层面上运作。根据这一理论,每个人都有两种潜在的结果:如果个人接受治疗,将会观察到的结果,以及如果个人没有接受治疗,将会观察到的结果。Rubin的理论表明,一种治疗的因果效应可以通过比较每个人观察到的结果和未观察到的潜在结果之间的差异来估计。由于发现的因果关系背后的不确定性和模糊性,测量两个变量之间的因果效应程度是另一个重要问题。许多独立的历史研究已经解决了因果关系测量的问题。这些测量方法包括休谟的恒定连接概念[40],Eells和Suppes将概率的提高作为因果关系的度量,以及Judea Pearl的因果度量。
同时涌现和因果也是相互联系的:一方面,涌现是复杂系统中各组成部分之间复杂的非线性相互作用的因果效应;另一方面,涌现特性也会对复杂系统中的个体产生因果关系。因此,可以借助因果来定量刻画涌现的发生。2013美国理论神经生物学家Erik Hoel尝试将因果引入涌现的衡量,提出了因果涌现这一概念,并且使用有效信息(Effective Information,简称EI)来量化系统动力学的因果性强弱[1][2]。因果涌现很好的刻画了系统宏观和微观状态之间的区别与联系,同时把人工智能中的因果和复杂系统中的涌现这两个核心概念结合起来,因果涌现也为学者回答一系列的哲学问题提供一个定量化的视角。比如,可以借助因果涌现框架讨论生命系统或者社会系统中的自上而下的因果等特性。这里的自上而下因果指的是向下因果[13],表示存在宏观到微观的因果效应。例如,壁虎断尾现象,当遇到危险时壁虎不征求尾巴的建议直接将自己的尾巴断掉,这里整体是因,尾巴是果,那么就存在一个整体指向个体的因果力。
基本概念
如果通过合适的粗粒化策略使得系统在宏观尺度能够展现出比它在微观尺度上具有更强的因果特性的时候,这就发生了因果涌现。其中系统因果关系的强度揭示其未来状态受当前状态影响的程度。值得注意的是,目前研究因果涌现都是建立在马尔可夫动力学系统上,同时也需要使用粗粒化函数。马尔可夫动力学是指系统的下一时刻状态只依赖于系统上一时刻的状态,并且与再之前的状态无关。马尔可夫动力学可以具体分为离散时间、连续时间,离散状态、连续状态,以及它们的组合等多种形式。粗粒化是一种通过将系统组件分组为更大、变化更慢的单元来简化系统描述的过程,它通常用于确定系统的基本特征,这些特征决定了系统的宏观行为,而不受微观尺度相互作用等细节的影响。对于复杂系统来说,粗粒化一般包含了节点(单元)的合并,以及宏观状态的计算两个步骤。粗粒化策略可以将一组微观状态映射到一个特定的宏观状态。此外,人们往往会混用粗粒化与重整化[14][15],确实两者存在很多共同之处,如两者都是对系统进行更加宏观尺度的描述。但是两者也存在区别,粗粒化一般都是对系统的状态进行操作,而重整化一般针对的是系统动力学、配分函数或者规则。粗粒化在不同领域有着不同的表述:下采样、池化等。下面我们分别介绍状态空间和变量空间下的马尔可夫动力学和粗粒化函数。
状态空间
马尔可夫动力学(状态转移矩阵)
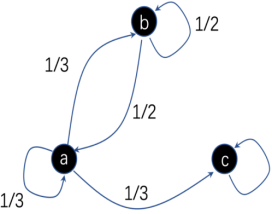
表中概率转移矩阵就定义了一个离散时间、离散状态上的马尔可夫动力学[math]\displaystyle{ P(S_{t+1}|S_{t}) }[/math],[math]\displaystyle{ S_t }[/math]和[math]\displaystyle{ S_{t+1} }[/math]分别表示[math]\displaystyle{ t }[/math]时刻和[math]\displaystyle{ t+1 }[/math]时刻的状态:
| states | a | b | c | d |
|---|---|---|---|---|
| a | 1/3 | 1/3 | 1/3 | 0 |
| b | 1/3 | 1/3 | 1/3 | 0 |
| c | 1/3 | 1/3 | 1/3 | 0 |
| d | 0 | 0 | 0 | 1 |
这是一个离散时间离散状态([math]\displaystyle{ S=\{a,b,c,d\} }[/math])的马尔可夫动力学中的状态概率转移矩阵,其中每一行、列都对应一个状态,第i行第j列表示状态从第i个状态转移到第j个状态的概率。我们也可以等价地用状态转移图来表示。
目前对因果涌现的讨论大多集中于这种离散时间、离散状态的马尔可夫动力学。
状态空间的粗粒化
状态空间的粗粒化表示对原始的状态转移矩阵进行分组合并成一些宏观的状态,然后定义宏观状态转移矩阵,下表是对上表的状态转移矩阵进行粗粒化后的宏观状态转移矩阵,将前三个状态粗粒化成一个宏观状态,从而构成了一个确定的转移关系。
| states | A | B |
|---|---|---|
| A | 1 | 0 |
| B | 0 | 1 |
变量空间
马尔可夫动力学
当然,还存在着连续时间、连续状态的马尔可夫动力学,例如朗之万方程:
[math]\displaystyle{ \frac{dX}{dt} =f(X) + \xi }[/math]
其中[math]\displaystyle{ X }[/math]为一随机变量,可以从所有实数中取值,f为一函数描述确定性动力学的速度如何随X而变,[math]\displaystyle{ \xi }[/math]为一高斯噪声。类似的也包括福克-普朗克方程等。
此外,布尔网络也可以看作是离散变量的马尔可夫动力学,每个节点就是一个变量,特殊的在于每个变量存在两个状态,可以将其转换成状态转移矩阵。
变量空间的粗粒化
变量空间的粗粒化表示对原始的变量进行分组合并成一些宏观的变量,从而构成宏观的马尔可夫动力学。
因果涌现的量化
几种因果涌现理论
近年来一些研究人员也提出一些定量刻画因果涌现的方法。对于如何定义因果涌现是一个关键问题,有三个代表性工作,分别是Hoel等[1][2]提出的基于粗粒化的方法、Rosas等[16]提出的基于信息分解的方法以及张江等人基于奇异值分解提出了一套新的因果涌现理论。
Erik Hoel的因果涌现理论
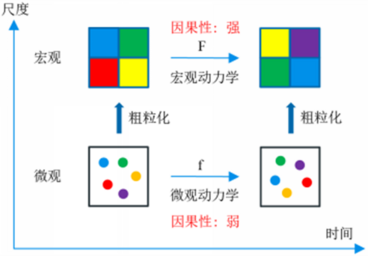
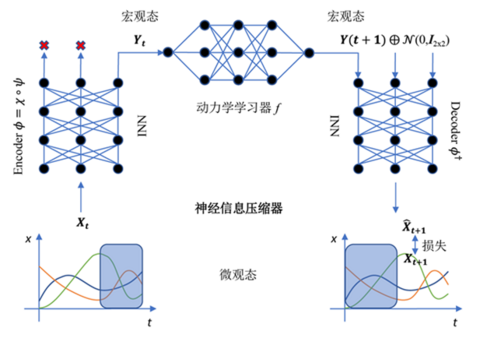
Hoel等[1][2]最早提出因果涌现理论,右图是对该理论框架的一个抽象,其中,横坐标表示时间尺度,纵坐标表示空间尺度。该框架可以看成是一个多层级的系统,存在微观和宏观两种状态。由于微观态往往具有很大的噪音,导致微观动力学的因果性比较弱,所以如果能对微观态进行合适的粗粒化得到噪音更小的宏观态,从而能使得宏观动力学的因果性更强。此外,因果涌现现象的发生意味着,当粗粒化微观状态时,从当前状态传递到下一状态的有效信息量会增加。
作者借鉴了整合信息的量化方法[17],提出一种因果效应度量指标有效信息([math]\displaystyle{ EI }[/math])来量化一个马尔可夫动力学的因果性强弱,该指标反应一个特定的状态如何有效地影响系统的未来状态,是系统动力学的内禀属性。具体来说,使用干预操作对上一时刻的状态做干预,然后计算干预分布与在干预的情况下经过动力学的下一时刻分布两者之间的互信息作为因果效应的度量指标, [math]\displaystyle{ EI }[/math]的计算公式如下所示:
[math]\displaystyle{ EI\left(S\right)=MI\left(I_D;E_D\right)=\sum_{i\in I_D}\ p\left(do\left(s_{t-1}=i\right)\right)\sum_{s_t\in E_D}{p\left(s_t\middle|\ d\ o\left(s_{t-1}=i\right)\right)}\log_2{\frac{p\left(s_t\middle|\ d\ o\left(s_{t-1}=i\right)\right)}{p\left(s_t\right)}}\ }[/math]
其中[math]\displaystyle{ s_{t-1} }[/math]和[math]\displaystyle{ s_t }[/math]分别表示[math]\displaystyle{ t-1 }[/math]和[math]\displaystyle{ t }[/math]时刻的系统状态,[math]\displaystyle{ I_D=do(S_{t-1}\sim U(I)) }[/math],[math]\displaystyle{ E_D=S_t\ |do(S_{t-1}\sim U(I)) }[/math],这里[math]\displaystyle{ do }[/math]操作表示对状态进行干预并且强行设定上一时刻的状态[math]\displaystyle{ s_{t-1} }[/math]为均匀分布,这里[math]\displaystyle{ I }[/math]表示系统的状态空间,[math]\displaystyle{ U\left ( I \right ) }[/math]表示空间上的均匀分布。进行干预操作是为了使得有效信息能客观衡量动力学的因果特性而不受原始输入数据的分布影响。为了消除状态空间大小对有效信息的影响,使得比较不同的尺度下的有效信息是有意义的,作者定义了一个归一化指标有效系数来衡量动力学的因果性强弱,有效系数和有效信息有如下关系:
[math]\displaystyle{ Eff(S)=\frac{EI(S)}{\log_2 n} }[/math]
其中[math]\displaystyle{ n }[/math]表示系统的状态个数,[math]\displaystyle{ Eff(S)\in[0,1] }[/math]。此外,有效系数可以进一步分解为确定性和简并性,[math]\displaystyle{ Eff\left(S\right)=\left \langle \text { 确定性 }\left ( s_0 \right )\right\rangle-\left \langle \text { 简并性 }\left ( s_0 \right )\right \rangle }[/math],确定性和简并性的计算公式分别如下所示:
[math]\displaystyle{ \text { 确定性 }\left(s_0\right)=\frac{1}{\log _2 n} \sum_{s_t \in E_D} p\left(s_t \mid d o\left(s_{t-1}=s_0\right)\right) \log _2\left(n \cdot p\left(s_t \mid d o\left(s_{t-1}=s_0\right)\right)\right) }[/math]
[math]\displaystyle{ \text { 简并性 }\left(s_0\right)=\frac{1}{\log _2 n} \sum_{s_t \in E_D} p\left(s_t \mid d o\left(s_{t-1}=s_0\right)\right) \log _2\left(n \cdot p\left(s_t\right)\right) }[/math]
可以通过比较系统中宏微观动力学的有效信息大小来判断因果涌现的发生。如果通过有效的粗粒化使得宏观动力学的有效信息大于微观动力学的有效信息([math]\displaystyle{ EI\left ( S_M \right )\gt EI\left (S_m \right ) }[/math]),那么认为在该粗粒化基础上宏观动力学具有因果涌现特性。
Rosas的因果涌现理论
Hoel提出的基于粗粒化的方法来量化系统中的因果涌现需要预先提供系统的状态转移矩阵以及粗粒化策略,然而现实情况是,往往只能获得系统的观测数据。为了克服这两个困难,Rosas等[16]从信息理论视角出发,提出一种基于信息分解方法来定义系统中的因果涌现,这里发生因果涌现有两种可能性:因果解耦(Causal Decoupling)和向下因果(Downward Causation),其中因果解耦表示宏观态对其他宏观态的因果效应,向下因果表示宏观态对于微观元素的因果效应。具体地,定义微观状态输入为[math]\displaystyle{ X_t\ (X_t^1,X_t^2,…,X_t^n ) }[/math],[math]\displaystyle{ V_t }[/math]表示宏观状态是[math]\displaystyle{ X_t }[/math]的随附特征,[math]\displaystyle{ X_{t+1} }[/math]和[math]\displaystyle{ V_{t+1} }[/math]分别表示下一时刻的微观和宏观状态。该方法建立在Willian和Beer等[18]提出的多元信息非负分解的基础上,Beer使用偏信息分解(PID)将微观态[math]\displaystyle{ X(X^1,X^2 ) }[/math]与宏观态[math]\displaystyle{ V }[/math]之间的互信息分解为四个部分,计算公式如下所示:
[math]\displaystyle{ I(X^1,X^2;V)=Red(X^1,X^2;V)+Un(X^1;V│X^2 )+Un(X^2;V│X^1 )+Syn(X^1,X^2;V) }[/math]
其中[math]\displaystyle{ Red(X^1,X^2;V) }[/math]表示冗余信息,是指两个微观态[math]\displaystyle{ X^1 }[/math]和[math]\displaystyle{ X^2 }[/math]同时给宏观态[math]\displaystyle{ V }[/math]提供的信息;[math]\displaystyle{ Un(X^1;V│X^2 ) }[/math]和[math]\displaystyle{ Un(X^2;V│X^1 ) }[/math]表示特有信息,是指每一个微观态单独给宏观态提供的信息;[math]\displaystyle{ Syn(X^1,X^2;V) }[/math]表示协同信息,是指所有微观态[math]\displaystyle{ X }[/math]联合给宏观态[math]\displaystyle{ V }[/math]提供的超过各自给宏观态提供的信息。
然而,PID框架只能分解关于多个原变量和一个目标变量之间的互信息,Rosas扩展了该框架,提出整合信息分解方法[math]\displaystyle{ \varphi ID }[/math][19]来处理多个原变量和多个目标变量之间的互信息,可以用来分解不同时刻间的互信息,作者基于分解后的信息提出了两种因果涌现的定义方法:
1)当特有信息[math]\displaystyle{ Un(V_t;X_{t+1}| X_t^1,\ldots,X_t^n\ )\gt 0 }[/math],表示当前时刻的宏观态[math]\displaystyle{ V_t }[/math]能超过当前时刻的微观态[math]\displaystyle{ X_t }[/math]给下一时刻的整体系统[math]\displaystyle{ X_{t+1} }[/math]再多提供一些信息,存在因果涌现;
2)绕开了选择特定的宏观态[math]\displaystyle{ V_t }[/math],仅仅基于系统当前时刻的微观态[math]\displaystyle{ X_t }[/math]和下一时刻的微观态[math]\displaystyle{ X_{t+1} }[/math]之间的协同信息定义因果涌现,当协同信息[math]\displaystyle{ Syn(X_t^1,…,X_t^n;X_{t+1}^1,…,X_{t+1}^n )\gt 0 }[/math],系统发生了因果涌现。其中[math]\displaystyle{ Un(V_t;X_{t+1}| X_t\ )\le Syn(X_t;X_{t+1}\ ) }[/math]衡成立。
值得注意的是,对于方法一判断因果涌现的发生需要依赖宏观态[math]\displaystyle{ V_t }[/math]的选择,然而[math]\displaystyle{ V_t }[/math]的选择又是很困难的,因此该方法不可行。一种自然的想法就是使用第二种方法借助协同信息来判断因果涌现的发生,但是由于冗余信息存在计算的问题,而协同信息的计算又依赖冗余信息。因此,第二种方法基于协同信息的计算往往也是不可行的。总之,这两种因果涌现的定量刻画方法都存在一些缺点,因此,更加合理的量化方法有待提出。
基于可逆性的因果涌现理论
张江等人基于奇异值分解,提出了一套新的因果涌现理论。给定一个系统的马尔科夫转移矩阵[math]\displaystyle{ P }[/math],通过对它进行奇异值分解,得到两个正交且的归一化矩阵[math]\displaystyle{ U }[/math]和[math]\displaystyle{ V }[/math],和一个对角阵[math]\displaystyle{ \Sigma }[/math]:[math]\displaystyle{ P= U\Sigma V^T }[/math]
我们可以将奇异值的[math]\displaystyle{ \alpha }[/math]次方的和定义为马尔科夫动力学的可逆性度量,即: [math]\displaystyle{ \Gamma_{\alpha}\equiv \sum_{i=1}^N\sigma_i^{\alpha} }[/math]
这里,[math]\Gamma_{\alpha}[/math]为近似动力学可逆性指标,[math]\sigma_i[/math]为概率转移矩阵[math]\displaystyle{ P }[/math]的奇异值,并且按照从大到小的顺序排列,[math]\alpha\in(0,2)[/math]为一个指定的参数,它起到让[math]\Gamma_{\alpha}[/math]能够更多地反映确定性还是简并性这样一种权重或倾向性。通常情况下,我们取[math]\alpha=1[/math],这可以让[math]\Gamma_{\alpha}[/math]能够在确定性与简并性之间达到一种平衡。
此外,文献中作者证明了EI与动力学可逆性[math]\Gamma_{\alpha}[/math]之间存在着一种近似的关系:
[math]\displaystyle{ EI\sim \log\Gamma_{\alpha} }[/math]
如果[math]\displaystyle{ P }[/math]的秩为[math]\displaystyle{ r }[/math],即从第[math]\displaystyle{ r+1 }[/math]个奇异值开始,奇异值都为0,则我们称动力学[math]\displaystyle{ P }[/math]存在着清晰的因果涌现(Clear Causal Emergence),并且因果涌现的数值为:[math]\displaystyle{ \Delta \Gamma_{\alpha} = \Gamma_{\alpha}(1/r-1/N) }[/math]
如果矩阵[math]\displaystyle{ P }[/math]满秩,但是对于任意给定的小数[math]\displaystyle{ \epsilon }[/math],存在[math]\displaystyle{ r }[/math],使得从[math]\displaystyle{ r+1 }[/math]开始,所有的奇异值都小于[math]\displaystyle{ \epsilon }[/math],则称系统存在着程度的模糊的因果涌现(Vague Causal Emergence),且因果涌现的数值为:[math]\displaystyle{ \Delta \Gamma_{\alpha}(\epsilon) = \frac{\sum_{i=1}^{r} \sigma_{i}^{\alpha}}{r} - \frac{\sum_{i=1}^{N} \sigma_{i}^{\alpha}}{N} }[/math]
总结来看,该定量化因果涌现的方法好处在于不依赖于具体的粗粒化策略,因而可以更加客观地量化因果涌现。其缺点是不能像[math]\displaystyle{ EI }[/math]那样分解为确定度和简并度两个分量,并且该方案需要事先给定系统的动力学。
其他(Dynamic independence等)
因果涌现的识别
前面已经介绍了一些通过因果关系和其他信息理论概念来量化涌现的工作。然而,在实际应用中,往往只能收集到观测数据,无法得到系统的真实动力学。因此,从可观测数据中辨别系统中因果涌现的发生是一个更为重要的问题。此外,在因果涌现的识别问题中往往希望寻找一个最优的宏观尺度,使其有效信息达到最大值,此时的系统具有最大因果力,并且能以最可靠、最有效的方式预测未来的状态。下面介绍两种因果涌现的识别方法,包括基于互信息的近似方法和神经信息压缩方法。
基于互信息的近似方法
由于基于互信息的近似方法需要依赖宏观态[math]\displaystyle{ V }[/math]的选择,因此,作者给出了两种方法,一种是给定一个宏观态[math]\displaystyle{ V }[/math]计算,另一种是基于机器学习的方法学习观态[math]\displaystyle{ V }[/math]以及最大化[math]\displaystyle{ \mathrm{\Psi} }[/math]。下面我们分别介绍这两种方法:
Rosas虽然给出因果涌现的严格定义,但在[math]\displaystyle{ \varphi ID }[/math]中使用的数学公式很复杂,同时计算要求很高,难以将该方法应用于实际系统。因此,Rosas等绕开特有信息和协同信息的计算[16],提出一个判定因果涌现发生的充分条件,基于互信息提出三个新指标,[math]\displaystyle{ \mathrm{\Psi} }[/math] ,[math]\displaystyle{ \mathrm{\Delta} }[/math] 和[math]\displaystyle{ \mathrm{\Gamma} }[/math]用于识别系统中的因果涌现,三种指标的具体计算公式如下所示:
[math]\displaystyle{ \Psi_{t, t+1}(V):=I\left(V_t ; V_{t+1}\right)-\sum_j I\left(X_t^j ; V_{t+1}\right) }[/math]
当[math]\displaystyle{ \mathrm{\Psi}\gt 0 }[/math]时,宏观状态会发生涌现,但是当[math]\displaystyle{ \mathrm{\Psi}\lt 0 }[/math],我们不能确定[math]\displaystyle{ V }[/math]是否发生涌现。
[math]\displaystyle{ \Delta_{t, t+1}(V):=\max _j\left(I\left(V_t ; X_{t+1}^j\right)-\sum_i I\left(X_t^i ; X_{t+1}^j\right)\right) }[/math]
当[math]\displaystyle{ \mathrm{\Delta}\gt 0 }[/math]时,宏观状态[math]\displaystyle{ V }[/math]发生向下因果。
[math]\displaystyle{ \Gamma_{t, t+1}(V):=\max _j I\left(V_t ; X_{t+1}^j\right) }[/math]
当[math]\displaystyle{ \mathrm{\Delta}\gt 0 }[/math]且[math]\displaystyle{ \mathrm{\Gamma}=0 }[/math]时,宏观状态[math]\displaystyle{ V }[/math]发生因果涌现且发生因果解耦。
该方法避开讨论粗粒化策略。但是也存在很多缺点:1)该方法提出的三个指标 ,[math]\displaystyle{ \mathrm{\Psi} }[/math] ,[math]\displaystyle{ \mathrm{\Delta} }[/math] 和[math]\displaystyle{ \mathrm{\Gamma} }[/math]只是基于互信息计算没有考虑因果,同时该方法得到的仅仅是发生因果涌现的充分条件;2)该方法无法得到显式的宏观动力学以及粗粒化策略,然而这两项对于下游的任务往往十分重要;3)当系统具有大量冗余信息或具有许多变量时,该方法的计算复杂度仍然很高。因此,该方法不是一种最优的方法,基于数据驱动的神经信息压缩方法应运而生。
基于机器学习的方法学习宏观态[math]\displaystyle{ V }[/math]以及最大化[math]\displaystyle{ \mathrm{\Psi} }[/math]:使用[math]\displaystyle{ f_{\theta} }[/math]神经网络来学习将微观输入[math]\displaystyle{ X_t }[/math]粗粒化成宏观输出[math]\displaystyle{ V_t }[/math],同时使用神经网络[math]\displaystyle{ g_{\phi} }[/math]和[math]\displaystyle{ h_{\xi} }[/math]来分别学习[math]\displaystyle{ I(V_t;V_{t+1}) }[/math]和[math]\displaystyle{ \sum_i(I(V_{t+1};X_{t}^i)) }[/math]两者互信息的计算,最后通过最大化两者之间的差(即[math]\displaystyle{ \mathrm{\Psi} }[/math])来优化学习。
神经信息压缩方法
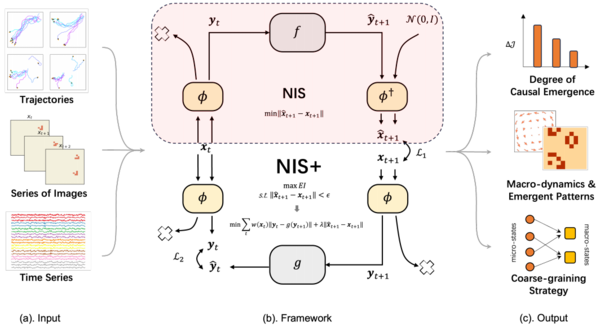
近年来,新兴的人工智能技术已经攻克一系列重大难题,同时机器学习方法配备了各种精心设计的神经网络结构和自动微分技术,可以在巨大的函数空间中逼近任何函数。因此,张江等[20]尝试基于神经网络提出了一种基于数据驱动的能够从时间序列数据中识别系统中的因果涌现方法,该方法能自动提取有效的粗粒度策略和宏观动力学,克服了信息分解方法中的种种不足。
在该工作中,输入的是时间序列数据[math]\displaystyle{ (X_1,X_2,...,X_T ) }[/math],可以使用如下的微方方程表示:
[math]\displaystyle{ \frac{d X}{d t}=f(X(t), \xi) }[/math]
其中[math]\displaystyle{ \xi }[/math]表示系统中的噪音。
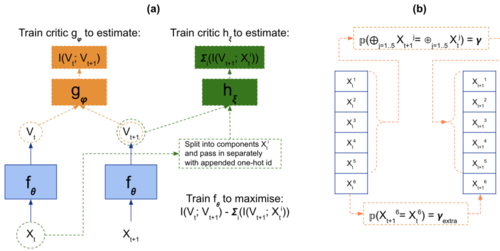
为了识别系统中的因果涌现,作者提出一种神经信息压缩方法,构建Encoder-Dynamic Learning-Decoder框架,该模型由编码器、动力学学习器以及解码器三个部分构成,用神经网络构建动力学学习器([math]\displaystyle{ f }[/math]),用可逆神经网络(INN)构建编码器(Encoder)和解码器(Decoder)。该模型框架可以看成是一个神经信息压缩器,将包含噪音的微观态压缩成宏观态,丢弃无用的信息,从而使得宏观动力学的因果性更强。NIS方法的模型框架如图所示。
具体来说,模型输入是微观状态[math]\displaystyle{ X_t\ (X_t^1,X_t^2,…,X_t^p ) }[/math],[math]\displaystyle{ p }[/math]表示输入数据的维数,输出预测下一个时刻的微观状态[math]\displaystyle{ \hat{X}_{t+1}\left(\hat{X}_{t+1}^1, \hat{X}_{t+1}^2, \ldots, \hat{X}_{t+1}^p\right) }[/math],该方法的目标函数是希望保证微观状态预测误差很小的条件下最大化有效信息,在保证预测误差约束足够小的情况下,NIS方法可以避免trivial解的出现。具体计算公式如下所示:
[math]\displaystyle{ \max _{\Phi_q, \hat{f}_q, \Phi_q^{\dagger}, q} E I\left(f_{\Phi_q}\right) \quad \text{s.t.}\left\|\Phi_q^{\dagger}(Y(t+1))-X_{t+1}\right\|\lt \epsilon }[/math]
最终希望得到有效的粗粒化维度[math]\displaystyle{ q }[/math]、粗粒化策略[math]\displaystyle{ \mathrm{\Phi}_q }[/math]和宏观动力学[math]\displaystyle{ {\hat{f}}_{\mathrm{\Phi}_q} }[/math],然而由于该目标函数是一个泛函优化问题,往往很难优化。为了解决这个问题,作者将优化过程分为两个阶段,第一个阶段表示在给定宏观尺度[math]\displaystyle{ q }[/math]的情况下[math]\displaystyle{ \min _{\Phi_q, \hat{f}_q, \Phi_q^{\dagger}}\left\|\Phi_q^{\dagger}(Y(t+1))-X_{t+1}\right\|\lt \epsilon }[/math],第二阶段将复杂的函数优化问题转换成线性搜索不同的[math]\displaystyle{ q }[/math],使得找到有效信息最大的宏观尺度[math]\displaystyle{ \mathop{max}\limits_{q}EI(\hat{f}_{\Phi_q}^\ast) }[/math] 。
除了能基于时序数据自动识别因果涌现,该框架还有很好的理论证明,其中有两个重要定理,定理一:神经信息挤压器的信息瓶颈,即对于任意的双射[math]\displaystyle{ \mathrm{\Psi}_\alpha }[/math]、投影[math]\displaystyle{ \chi_q }[/math]、宏观动力学[math]\displaystyle{ f }[/math]以及高斯噪音[math]\displaystyle{ z_{p-q}\simΝ\left (0,I_{p-q}\right ) }[/math],[math]\displaystyle{ I\left(Y_t;Y_{t+1}\right)=I\left(X_t;{\hat{X}}_{t+1}\right) }[/math]恒成立,这意味着,编码器丢弃的所有信息实际上都是与预测无关的纯粹噪声;定理二:对于一个训练好的模型,[math]\displaystyle{ I\left(X_t;{\hat{X}}_{t+1}\right)\approx I\left(X_t;X_{t+1}\right) }[/math]。因此,综合定理一和定理二,可以得到对于一个训练好的模型[math]\displaystyle{ I\left(Y_t;Y_{t+1}\right)\approx I\left(X_t;X_{t+1}\right) }[/math]。
该工作的一个重要优点就是该框架能同时处理离散和连续动力学系统,通过将神经网络看作是给定输入条件下的高斯分布[math]\displaystyle{ p\left(Y| X\right) }[/math],可以定义新的有效信息计算公式,公式如下所示:
[math]\displaystyle{ \begin{gathered}EI_L(f)=I(do(X\sim U([-L,L]^n));Y)\approx-\frac{n+nln(2\pi)+\sum_{i=1}^n\sigma_i^2}2+nln(2L)+\operatorname{E}_{X\sim U([-L,L]^n)}(ln|det(\partial_{X^{\prime}}f(X)))|)\end{gathered} }[/math]
其中[math]\displaystyle{ U\left(\left[-L, L\right]^n\right) }[/math]表示范围在[math]\displaystyle{ \left[-L ,L\right] }[/math]上的[math]\displaystyle{ n }[/math]维均匀分布,[math]\displaystyle{ \sigma_i }[/math]是输出[math]\displaystyle{ Y_i }[/math]的标准差,可以通过[math]\displaystyle{ Y_i }[/math]的均方误差来估计,[math]\displaystyle{ det }[/math]表示函数[math]\displaystyle{ f }[/math]的雅可比行列式。为了消除有效信息计算公式会受到输入维度的影响,作者定义了新的有效信息计算公式[math]\displaystyle{ d E I_L(f) }[/math],具体公式如下所示:
[math]\displaystyle{ dEI_L(f)\approx-\frac{1+ln(2\pi)+\sum_{i=1}^n\frac{\sigma_i^2}n}2+ln(2L)+\frac1n\mathrm{E}_{X\sim U([-L,L]^n)}(ln|det(\partial_{X^{\prime}}f(X)))|) }[/math]
NIS框架与前面章节中提到的计算力学存在很多相似之处,NIS可以被视为一种[math]\displaystyle{ \epsilon - machine }[/math],所有历史过程构成的集合[math]\displaystyle{ \overleftarrow{S} }[/math]可以看作是微观状态,所有[math]\displaystyle{ R \in \mathcal{R} }[/math]表示宏观状态,函数[math]\displaystyle{ \eta }[/math]可以理解为一种粗粒化函数,[math]\displaystyle{ \epsilon }[/math]可以理解为一种有效的粗粒化策略,[math]\displaystyle{ T }[/math] 对应于有效的宏观动力学。最小随机性特征表征了宏观动力学的确定性,在因果涌现中可以用有效信息衡量。当整个框架训练足够充分的时候,可以精确地预测未来的微观状态时,编码的宏观状态收敛到有效状态,而有效状态可以被视为计算力学中的因果状态。
同时NIS方法与前面提到的G-emergence也有相似之处,例如,NIS同样采用了格兰杰因果的思想:通过预测下一个时间步的微观状态来优化有效的宏观状态。然而,这两个框架之间有几个明显的区别:a)在G-emergence理论中,宏观状态需要人工选择,然后NIS中是通过自动优化粗粒化策略来得到宏观状态;b)NIS使用神经网络来预测未来状态,而G-emergence使用自回归技术来拟合数据。
但是该方法存在一些不足,作者将优化过程分为两个阶段,但是没有真正的最大化有效信息。因此,杨等人进一步改进该方法,通过引入反向动力学以及重加权技术借助变分不等式将原始的最大化有效信息转换成最大化其变分下界来直接优化目标函数。目标函数可以被定义为在给定微观预测足够小的情况下最大化宏观动力学的有效信息:
[math]\displaystyle{ \max_{\phi,f_q,\phi^+} \mathcal{J}(f_q), }[/math]
[math]\displaystyle{ s.t. || \hat{\boldsymbol{x}}_{t+1}-\boldsymbol{x}_{t+1} || \lt \epsilon , }[/math]
[math]\displaystyle{ \hat{\boldsymbol{x}}_{t+1}=\phi^{\dag}(f_q(\phi(\boldsymbol{x}_t))) }[/math]
将最大化问题转化为带有约束的最小化问题:
[math]\displaystyle{ \min_{\omega,\theta,\theta'} \sum_{i=0}^{T-1}w(\boldsymbol{x}_t)||\boldsymbol{y}_t-g_{\theta'}(\boldsymbol{y}_{t+1})||+\lambda|| \hat{\boldsymbol{x}}_{t+1}-\boldsymbol{x}_{t+1} || }[/math]
实例
离散马尔科夫链比较
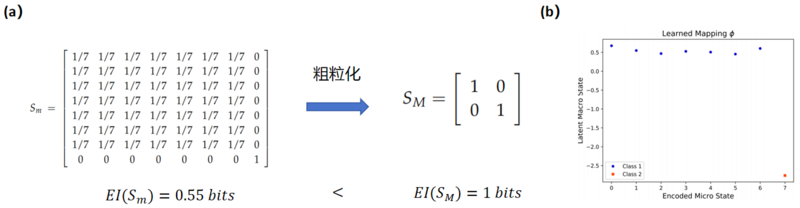
在文献中,Hoel给出一个含有8个状态的马尔可夫链的状态转移矩阵例子,如图a所示。其中前7个状态之间等概率转移,最后一个状态是独立的,通过将前7个状态粗粒化成一个状态,可以得到右图确定的宏观系统,即系统的未来状态完全可以由当前状态决定。此时[math]\displaystyle{ EI(S_M\ )\gt EI(S_m\ ) }[/math],系统发生了因果涌现。同样在张提出的NIS方法中也对这个例子进行了实验,结果发现在scale=1时,因果涌现最显著,通过将这个8个状态进行one-hot编码输入到模型中,得到scale=1的宏观态的数值正好可以将这8个状态分为2组,其中前7个状态一组,最后一个状态一组,与Hoel的例子的结论是一致的。
鸟群以及脑系统比较
应用
主要讲解因果涌现的潜在应用, 包括: 生物系统、神经网络、脑神经系统、人工智能(因果表示学习、基于世界模型的强化学习)、中医等。
这些定量的量化因果涌现的方法已经广泛应用到很多复杂系统中,包括具有成百上千节点的复杂网络以及神经网络,到具有明显涌现现象的生命游戏、鸟群模型、蛋白质交互、生物以及真实的大脑网络等。 生物系统、神经网络、脑神经系统、人工智能(因果表示学习、基于世界模型的强化学习)、中医等 在复杂网络上的应用 2020年,Klein和Hoel改进此前提出的基于粗粒化的方法并将其应用到复杂网络中[21],作者借助随机游走子来定义网络中的马尔可夫链,将随机游走子放在节点上等价于对节点做干预,然后基于随机游走概率定义节点的转移概率矩阵。同时作者将有效信息与网络的连通性建立联系,网络中的连通性可以通过节点的出边和入边的权重的不确定性来表征,基于此定义复杂网络中的有效信息。
在随机网络(ER)、偏好依赖网络(PA)等人工网络以及四类真实网络中进行实验比较。对于ER网络来说,有效信息的大小只依赖于连接概率[math]\displaystyle{ p }[/math],并且随着网络规模的增大会收敛到[math]\displaystyle{ -log_2p }[/math]。同时一个关键发现表明,存在一个相变点,该相变点近似在网络的平均度([math]\displaystyle{ \lt k\gt }[/math])等于[math]\displaystyle{ log_2N }[/math]的位置,同样对应于ER网络随着连接概率增加而出现巨连通集团的相变点位置,超过该相变点随机网络结构不会随着其规模的增加而包含更多的信息。对于PA网络来说,[math]\displaystyle{ \alpha\lt 1.0 }[/math]时,有效信息的大小会随着网络规模的增加而增大;[math]\displaystyle{ \alpha\gt 1.0 }[/math]时,结论相反;[math]\displaystyle{ \alpha=1.0 }[/math]对应的无标度网络则是增长的临界边界。对于真实网络,作者发现,生物网络因为具有很大的噪音,所以有效信息最低,通过有效的粗粒化能去除这些噪音,相比于其他类型网络因果涌现最显著,而技术类型网络是更稀疏、非退化的,因此,平均效率更高,节点关系也更加具体,所有有效信息也最高。
在该文章中作者使用贪婪算法来构建宏观尺度的网络,然而对于大规模网络来说,效率仍然很低。随后,Griebenow等[22]提出了一种基于谱聚类的方法来识别偏好依附网络中的因果涌现。相比贪婪算法以及梯度下降算法,谱聚类算法的计算时间最少,同时找到的宏观网络的因果涌现也更加显著。
在生物系统上的应用 生物网络中充满噪音使得很难理解其内部的运作原理,这种噪音一方面来自系统的固有噪音,另一方面是由于测量或观察引入的, Klein等[23]进一步探索了生物网络中的噪声、简并性和确定性三者之间的关系以及具体含义。例如,基因表达网络中的高度确定性关系可以理解为一个基因几乎肯定会导致另一个基因的表达。同时生物系统在进化过程中也普遍存在简并现象,这两个原因导致目前尚不清楚在何种尺度上分析生物系统才能最好地理解它们的功能。Klein等[24]分析了超过1800个物种的蛋白质相互作用网络,发现宏观尺度的网络具有更小的噪音和简并性,同时与不参与宏观尺度的节点相比,组成宏观尺度交互群中的节点更具有弹性。因此,生物网络为了适应进化的要求,需要演化成宏观尺度以提高确定性来增强网络的弹性以及提高信息传输的有效性。
Hoel等[25]借助有效信息理论进一步研究生物系统中的因果涌现,作者将有效信息应用到基因调控网络中,识别最能提供信息的心脏发育模型从而控制哺乳动物的心脏发育。通过量化酿酒酵母基因网络的最大联通集团的因果涌现,揭示富有信息的宏观尺度在生物学中是普遍存在的以及生命机制本身也经常运行在宏观尺度上。该方法也为生物学家提供一个可计算的工具来识别最具有信息的宏观尺度,并且可以在此基础上建模、预测、控制和理解复杂的生物系统。
为验证猕猴运动有关的信息是其皮层活动的一个涌现特征,Rosas等尝试基于猕猴的皮质脑电图(ECoG)和动作捕捉(MoCap)数据进行实验,其中ECoG和MoCap分别由64个通道和3个通道的数据构成微观和宏观数据,由于最原始的MoCap数据不满足随附特征的条件独立假设,因此,作者使用偏最小二乘和支持向量机算法推断出与预测猕猴行为有关的编码在ECoG信号中的那部分神经活动,并推测该信息就是潜在神经活动的涌现特征,然后基于计算出来的宏观特征与微观状态验证因果涌现的存在。
Swain等[26]探索蚁群的交互历史对任务分配和任务切换的影响,使用有效信息研究噪声信息如何在蚂蚁之间进行传播。结果发现,蚁群之间历史交互程度影响任务的分配,并且具体交互中蚂蚁群体的类型决定交互中的噪音。此外,即使当蚂蚁切换功能群时,蚁群涌现出来的凝聚力也能保证群体的稳定,同时不同功能蚁群在维持蚁群凝聚力方面也发挥着不同的作用。
在人工神经网络上的应用,Marrow等[27]尝试引入一个基于信息论的指标即有效信息来量化和跟踪训练过程中DNN因果结构的变化,其中有效信息用于评估节点和边对每层下游目标的因果的影响程度。有效信息可以分解为灵敏性和简并性,通过观察模型训练过程中有效信息,包括灵敏性和简并性的变化就可以确定模型的泛化能力,从而帮助学者更好的理解和解释DNN的工作原理。
因果表示学习是人工智能中的一个新兴领域,它试图将机器学习中的两个重要领域:表示学习和因果推断结合起来。尝试结合两个子领域的优势,自动提取数据背后的重要特征和因果关系[28]。基于粗粒化的因果涌现识别可以等价于一种因果表示学习任务。从数据中识别因果关系的涌现,等价于学习数据背后的潜在因果关系。具体来说,宏观状态可以看成因果变量,动力学学习器类比因果机制,粗粒化策略可以看作是一个从原始数据到因果表示的编码过程,有效信息可以理解为对机制的因果效应强度的衡量。由于这两者存在很多相似之处,使得两个领域的技术和概念可以相互学习。例如,因果表征学习技术可以应用于识别因果涌现,反过来,学习到的抽象因果表征可以被解释为一种宏观状态,从而增加因果表征学习的可解释性。但是两者也存在一些差异,主要包括两点:1)因果表示学习假设其背后存在一个真实的因果机制,数据是由这个因果机制产生的,然而宏观层面涌现出的状态和动力学之间可能并不存在“真正的因果关系”;2)因果涌现中的粗粒化后的宏观状态是一种低维的描述,然而因果表示学习中没有这个要求。但是,从认识论的视角看,两者并不存在差异,因为两者所做的都是从观察数据中提取有效信息,从而获得具有因果效应更强的表征。
基于世界模型的强化学习假设其内部存在一个世界模型可以模拟智能体所面对的环境的动力学[29]。世界模型的动力学可以通过智能体与环境的相互作用来学习,该动力学也可以帮助智能体对不确定的环境做出计划和决策。同时为了表示复杂的环境,世界模型一定是对环境的粗粒度描述,一个典型的世界模型架构总是包含一个编码器和一个解码器。因此,基于世界模型的强化学习与因果涌现也存在很多相似之处。世界模型也可以被视为一种宏观动力学,环境中的所有状态可以看作是宏观状态,这些可以看成是压缩后的忽略无关信息的状态,能捕捉环境中最重要的因果特征,以便智能体做出更好的决策。在计划过程中,智能体也可以使用世界模型来模拟真实世界的动力学。因此,两个领域之间的相似性和共同特征可以帮助我们将一个领域的思想和技术借鉴到另一个领域。例如,具有世界模型的智能体可以将复杂系统作为一个整体来进行相互作用,并从相互作用中获得涌现的因果规律,从而更好的帮助我们做因果涌现识别任务。反过来,最大化有效信息技术也可以用于强化学习,使世界模型具有更强的因果特性。
相关领域研究
存在一些相关领域研究与因果涌现理论联系比较紧密,重点介绍与因果科学、因果模型抽象、模型约简、动力学模式分解以及马尔可夫链的简化的区别和联系。
因果科学
因果涌现与因果模型抽象
在复杂系统中,由于微观状态往往存在噪音,需要将微观状态进行粗粒化得到噪音更小的宏观状态,使得宏观动力学的因果性更强。同样对于因果模型也一样,由于原始模型过于复杂,或者计算资源受限,所以往往需要得到更加抽象的因果模型,并且保证抽象的模型尽可能保持原始模型的因果机制,因果模型抽象讨论的也是因果关系与模型抽象(可以看成粗粒化过程)之间的相互作用[30]。因此,因果涌现识别与因果模型抽象有很多相似之处,可以把原始的因果机制理解为微观动力学,抽象出来的机制理解为宏观动力学。在神经信息压缩框架中(NIS),对粗粒化策略和宏观动力学进行了限制,要求宏观动力学的微观预测误差要足够小以排除平凡解。这个要求也类似于因果模型抽象中希望抽象后的因果模型与原始模型的距离要尽可能相近。但是两者也存在一些不同:1)因果涌现中是对状态或数据进行粗粒化,而因果模型抽象是对模型进行操作;2)因果模型抽象中考虑混肴因子,然而却被因果涌现的讨论忽略。
模型约简
模型约简,就是要将高维的复杂系统动力学模型进行化简、降维,用低维的动力学来描述动力系统的演化规律,这一过程其实就是因果涌现研究中的粗粒化过程。将对大尺度动力系统的近似方法主要有两大类,即基于奇异值分解的近似方法和基于Krylov的近似方法。前者基于奇异值分解,后者基于矩匹配。虽然前者具有许多理想的性质,包括误差界,但它不能应用于高复杂度的系统。另一方面,后者的优势在于它可以迭代实现,因此适用于高复杂度系统。将这两个族的最佳属性相结合的努力导致了第三类近似方法,称为SVD/Krylov。两种方法都是基于粗粒化前后输出函数的误差损失函数。
所谓的大尺度动力学一般情况下,如果时间是连续的,就可以表示为
[math]\displaystyle{ \frac{dx}{dt}=f(x,u), z=g(x,u) }[/math]
其中[math]\displaystyle{ x\in\mathcal{R}^n }[/math]表示演化的变量,[math]\displaystyle{ f:\mathcal{R}^n\to\mathcal{R}^n }[/math] ,[math]\displaystyle{ u\in\mathcal{R}^m }[/math]是与[math]\displaystyle{ x }[/math]独立,但也会伴随系统演化的其他变量的组合,控制论中通常可以人工调控调系统整演化的方向,如果是随机噪声,就可以直接规定[math]\displaystyle{ u=\epsilon\sim\mathcal{N}(0,\Sigma) }[/math]。[math]\displaystyle{ g:\mathcal{R}^n\to\mathcal{R}^p }[/math]是演化中的输出值,用来观测系统的演化状况,粗粒化的损失信息就是看变化前后观测值的损失函数。
时间离散的情况下,系统就可以表示为
[math]\displaystyle{ x_{t+1}=f(x_t,u_t), z_t=g(x_t,u_t) }[/math]
对大尺度动力学进行约简,需要先对变量进行线性映射[math]\displaystyle{ y=Wx, W\in\mathcal{R}^{k\times n}, k\lt n }[/math]。这样就可以对我们动力系统模型进行简化,得到约简后的系统
[math]\displaystyle{ \frac{dy}{dt}=Wf(Vx,u), \hat{z}=g(Vx,u) }[/math]
或
[math]\displaystyle{ y_{t+1}=Wf(Vy_t,u_t), \hat{z}_t=g(Vx_t,u_t) }[/math]
其中[math]\displaystyle{ V\in\mathcal{R}^{n\times k}, WV=I_n }[/math],寻找合适的W也是以往研究的关键。
动力学模式分解
马尔可夫链的简化
参考文献
- ↑ 1.0 1.1 1.2 1.3 Hoel E P, Albantakis L, Tononi G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49): 19790-19795.
- ↑ 2.0 2.1 2.2 2.3 Hoel E P. When the map is better than the territory[J]. Entropy, 2017, 19(5): 188.
- ↑ Meehl P E, Sellars W. The concept of emergence[J]. Minnesota studies in the philosophy of science, 1956, 1239-252.
- ↑ Holland J H. Emergence: From chaos to order[M]. OUP Oxford, 2000.
- ↑ Anderson P W. More is different: broken symmetry and the nature of the hierarchical structure of science[J]. Science, 1972, 177(4047): 393-396.
- ↑ 6.0 6.1 J. P. Crutchfield, K. Young, Inferring statistical complexity, Physical review letters 63 (2) (1989) 105.
- ↑ 7.0 7.1 A. K. Seth, Measuring emergence via nonlinear granger causality., in: alife, Vol. 2008, 2008, pp. 545–552.
- ↑ C. R. Shalizi, C. Moore, What is a macrostate? subjective observations and objective dynamics, arXiv preprint cond-mat/0303625 (2003).
- ↑ C. R. Shalizi, Causal architecture, complexity and self-organization in time series and cellular automata, The University of Wisconsin-Madison, 2001.
- ↑ Pearl J. Causality[M]. Cambridge university press, 2009.
- ↑ Granger C W. Investigating causal relations by econometric models and cross-spectral methods[J]. Econometrica: journal of the Econometric Society, 1969, 424-438.
- ↑ Pearl J. Models, reasoning and inference[J]. Cambridge, UK: CambridgeUniversityPress, 2000, 19(2).
- ↑ 引用错误:无效
<ref>标签;未给name属性为:2的引用提供文字 - ↑ K. G. Wilson, J. Kogut, The renormalization group and the expansion, Physics reports 12 (2) (1974) 75–199.
- ↑ J. C. Collins, Renormalization, Cambridge university press, 2023.
- ↑ 16.0 16.1 16.2 Rosas F E, Mediano P A, Jensen H J, et al. Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data[J]. PLoS computational biology, 2020, 16(12): e1008289.
- ↑ Tononi G, Sporns O. Measuring information integration[J]. BMC neuroscience, 2003, 41-20.
- ↑ Williams P L, Beer R D. Nonnegative decomposition of multivariate information[J]. arXiv preprint arXiv:10042515, 2010.
- ↑ P. A. Mediano, F. Rosas, R. L. Carhart-Harris, A. K. Seth, A. B. Barrett, Beyond integrated information: A taxonomy of information dynamics phenomena, arXiv preprint arXiv:1909.02297 (2019).
- ↑ Zhang J, Liu K. Neural information squeezer for causal emergence[J]. Entropy, 2022, 25(1): 26.
- ↑ Klein B, Hoel E. The emergence of informative higher scales in complex networks[J]. Complexity, 2020, 20201-12.
- ↑ Griebenow R, Klein B, Hoel E. Finding the right scale of a network: efficient identification of causal emergence through spectral clustering[J]. arXiv preprint arXiv:190807565, 2019.
- ↑ Klein B, Swain A, Byrum T, et al. Exploring noise, degeneracy and determinism in biological networks with the einet package[J]. Methods in Ecology and Evolution, 2022, 13(4): 799-804.
- ↑ Klein B, Hoel E, Swain A, et al. Evolution and emergence: higher order information structure in protein interactomes across the tree of life[J]. Integrative Biology, 2021, 13(12): 283-294.
- ↑ Hoel E, Levin M. Emergence of informative higher scales in biological systems: a computational toolkit for optimal prediction and control[J]. Communicative & Integrative Biology, 2020, 13(1): 108-118.
- ↑ Swain A, Williams S D, Di Felice L J, et al. Interactions and information: exploring task allocation in ant colonies using network analysis[J]. Animal Behaviour, 2022, 18969-81.
- ↑ Marrow S, Michaud E J, Hoel E. Examining the Causal Structures of Deep Neural Networks Using Information Theory[J]. Entropy, 2020, 22(12): 1429.
- ↑ B. Sch ̈olkopf, F. Locatello, S. Bauer, N. R. Ke, N. Kalchbrenner, A. Goyal, Y. Bengio, Toward causal representation learning, Proceedings of the IEEE 109 (5) (2021) 612–634.
- ↑ D. Ha, J. Schmidhuber, World models, arXiv preprint arXiv:1803.10122 (2018).
- ↑ S. Beckers, F. Eberhardt, J. Y. Halpern, Approximate causal abstractions, in: Uncertainty in artificial intelligence, PMLR, 2020, pp. 606–615.
编者推荐
下面是一些链接能够帮助读者更好的了解因果涌现的相关信息:
因果涌现读书会
分享近期发展起来的一些理论与工具,包括因果涌现理论、机器学习驱动的重整化技术,以及自指动力学正在发展一套跨尺度的分析框架等。
涌现现象无非是复杂系统中诸多现象中最神秘莫测的一个,而Erik Hoel提出的“因果涌现”理论为这种跨层次的奇妙涌现现象提供了一种新的可能解释途径。通过跨层次的粗粒化(Coarse-graining, 或称重整化Renormalization)操作,我们便可以在同一个动力学系统上在不同的尺度得到完全不同的动力学,通过本季读书会梳理,我们希望探讨这一新兴领域的前沿进展,衍生更多新的研究课题。
涌现与因果的结合创造了因果涌现的概念。这是一套利用因果性来定量刻画涌现的理论体系,本季读书会通过阅读前沿文献,加深我们对因果、涌现等概念的理解;聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。第二季读书会更加集中在探讨因果科学与因果涌现之间的关系,以及对涌现进行定量刻画,聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。
因果涌现第三季的读书会中,将进一步围绕因果涌现的核心研究问题『因果涌现的定义』以及『因果涌现的辨识』来进行深入的学习和讨论,对 Erik Hoel 提出的 Causal Emergence,Causal Geometry 等因果涌现的核心理论进行深入的探讨和剖析,并且详细梳理其中涉及到的方法论,包括从动力学约简、隐空间动力学学习等其他研究领域中学习和借鉴相关的研究思路,最后探讨因果涌现的应用,包括基于生物网络、脑网络或者涌现探测等问题展开扩展,发掘更多的实际应用场景。
文章推荐
- Zhang, J.; Liu, K. Neural Information Squeezer for Causal Emergence. Entropy 2023, 25, 26.
文章提出了一种名为 "神经信息挤压器"(Neural Information Squeezer)的通用机器学习框架,能自动提取有效的粗粒化策略和宏观动力学,并直接从时间序列数据中识别因果涌现。
路径推荐
- 张江老师根据因果涌现读书会第一季梳理的关于因果涌现的学习路径:https://pattern.swarma.org/article/153
此词条由王志鹏编写,张江、王志鹏和江森-JS整理和审校。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。