多重分形

现实中的复杂系统一般都具有自相似特征，这种自相似性不仅仅体现为几何形体上的自相似，也体现为某种质量、测度在空间上的分配。例如，当我们考察人类城市中人口或者灯光在空间上的分布的时候，我们实际上在考查一个三维空间中的曲面。其中，曲面的横纵坐标分别是城市空间的经纬度，而高度坐标是对应经纬度点的人口或者灯光的密度值。然而，如果我们真的画出来这样的曲面，就会发现它并不光滑，而是非常地参差不齐，波动涨落非常剧烈的，因此传统的欧几里德几何工具以及微积分数学很难刻画。如果我们做这个曲面的等高线图，就会发现，每个等高线所包围的区域都是非常参差不齐的分形几何体。那么，我们该如何对这类不规则的空间分布进行刻画？多重分形（Multifractal）便是描述这类在不规则的分形空间之上质量分布的定量化工具。

一个例子

为了说清楚什么是多重分形，以及刻画多重分形的多重分形谱（Multifractal spectrum），我们先介绍一个简单的例子。这个例子通过往经典的康托尔集上赋予质量而形成一种非常不规则的一维地形。这种地形具有典型的多重分形特性。为了定量化这种特征，我们引入了多重分形谱这一数学工具。通过简单的计算以及数值试验，我们可以初步了解到多重分形的作用与功能，至于严格的定义与具体的计算方法则留给下一节详细说明。

康托尔尘

康托尔尘（学名康托尔集Cantor Set）是由大数学家乔治·康托尔提出来的一种一维的分形集。它的构造非常简单。我们把[0,1]闭区间三等分，形成三个闭区间：[0,1/3], (1/3,2/3), [2/3,1]，把中间的区间去掉，剩下[0,1/3], [2/3,1]，然后再对这两个闭区间分别进行同样的操作，即三等分，然后把中间的去掉。这个操作可以一直重复下去，直到无穷。最终形成的那个无穷小测度的集合就是所谓的康托尔集。

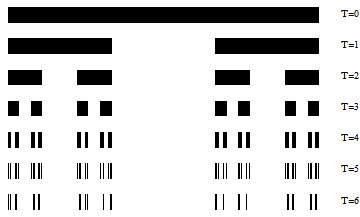
下图形象地展示了这个不断重复地构建过程（6步）：

这里列出了构造康托尔尘的Mathematica代码

NestList[Flatten[Map[Function[x,temp = x[[2]] - x[[1]]; {{x[[1]],x[[1]] + temp/3}, {x[[2]] - temp/3, x[[2]]}}], #], 1] &, {0,1}, n]

其中，n为迭代的步数。该程序能够返回每个步骤的小区间集合。

康托尔尘上的质量分布

康托尔尘是一个经典的分形(Fractal)，它的分形维数为ln2/ln3。下面，我们来构造多重分形，即给每个小区间赋予质量。具体地，我们也可以按照如下的步骤递归地进行下列操作： 首先，将[0,1]均分为三份，去掉中间的那个小区间，剩下两个小区间[0,1/3]和[2/3,1]。给左边的小区间分配质量1/3，右边的分配2/3。接下来再把[0,1/3]分为三份，去掉中间的小区间，剩下的两个小区间[0,1/9]和[2/9,1/3]，左边分1/3的质量，右边分2/3的质量，而[0,1/3]的小区间仅仅有1/3的质量，这样[0,1/9]这个小区间就分配到了1/3*1/3=1/9的质量，而[2/9,1/3]则分配到了2/3*1/3=2/9的质量……。这样，每对小区间划分一次，就把该小区间上的质量的1/3分到左边，把2/3分到右边。如此循环往复地进行下去。

我们用矩形的高度来表示小区间分配的质量，则上述分配过程可以形象地表达为下图：

多重分形谱

从图上可以看出，随着层次的不断加深，区间变得越来越碎，而质量在这些小区间上的分布就会越来越参差不齐（奇异性Singularity），但是对于每一个给定的层，所有小区间上的质量之和都为1，这是因为在不断加深层次的时候，质量在小区间上的分配都满足守恒律。我们可以用一个被称作多重分形谱的曲线来刻画这种奇异性。

首先，我们知道，在第t步的时候，任意一个小区间i的质量可以写成：

[math]\displaystyle{ m_i=p^x (1-p)^{t-x} }[/math]

其中p就表示在每一次划分的时候，分配到左边小区间的质量比率。例如，在上述例子中，每次1/3的质量划分给左侧区间的话，那么p=1/3。x表示的是该小区间i在t步生成过程中共有多少次被分配到了左侧，这样t-x对应的就是分配在右侧区间的次数。如下图所示，红色的线条就表示分到了左侧，绿色线条分配在右侧。

因此，在T=5这个层次的小区间中，质量为[math]\displaystyle{ p^x (1-p)^{t-x} }[/math]的区间可能不止一个，只要从T=1到T=5的任意一条路径中包含x个向左的分支，t-x个右分支，最终的质量就都一样。事实上，我们可以计算出来具有质量[math]\displaystyle{ m_i=p^x (1-p)^{t-x} }[/math]的小区间总共有[math]\displaystyle{ C_t^{x} }[/math]个。这样，对于层次t来说，我们得到了两个量：一个是小区间的质量[math]\displaystyle{ m_i=p^x (1-p)^{t-x} }[/math]，另一个是质量为m的小区间个数，我们记为：

[math]\displaystyle{ N(m_i)=C_t^{x} }[/math]

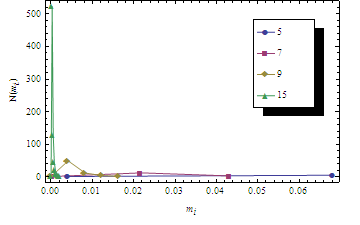
通过将上述两个等式中的x消去，我们不难找到N和m_i之间的函数关系，这个函数关系刻画了第t层小区间质量的分布情况。如下图所示，我们画出了不同t对应的N(m_i)曲线（不同的曲线对应不同的t）：

我们看到，当t逐渐变大的时候，这条曲线会变得越来越尖，这表示有很多小区间具有相同的质量值，而大部分区间质量参差不齐。这种图像不方便我们比较，我们需要想办法把这个尖抹平。一种简单易行的方法就是取对数坐标。然而，对数坐标的底取多少合适呢？我们当然可以设这个底为一个常数e，但是，考虑到无论N还是m_i以及小区间的大小都会随着t而呈现指数类型的增长或者衰减。因此，我们可以考虑对数底定为t层次每个小区间的长度大小，即3^-t。这样一来，我们便可以得到很规整的图形：

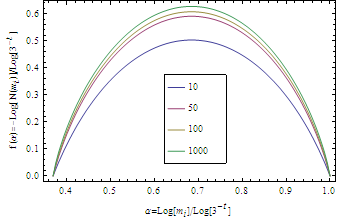
在该图中，我们画出了不同t所对应的[math]\displaystyle{ -\log_{(3^{-t})}(N(m_i)) }[/math]对[math]\displaystyle{ \log_{(3^{-t})}(m_i) }[/math]的曲线（取负号是因为该数值可以被解释为分形维，详见下一节的讨论。）。我们能看到，随着t逐的增大，曲线不仅仅没有出现高高的尖峰，而且逐渐趋近于一条光滑的闭合曲线。这是因为，随着t的增长，我们的对数之底也会快速地衰减，从而使得这条曲线会逐渐稳定。那么，当t趋于无穷大的时候，这条曲线就构成了康托尔集合上质量分布的多重分形谱。

多重分形谱的定义

实质上，上述作法不仅可以让质量在各个小区间上的分布图形更加好看，它还具有更深刻的含义。我们知道分形研究的是当我们的观察精度不断提高，被观察的几何形体是如何变化的。那么，当我们计算log(m_i)随着log(3^-t)而变化的时候，我们实质上是在计算质量如何随着观察分辨率的提高而衰减。更一般地，我们不妨把这个质量随观察精度而变化的速度定义为一个量：

[math]\displaystyle{ \alpha=\frac{\log(m_i)}{\log(b(t))} }[/math]

假设我们把一个集合划分成不同精度t的盒子，那么每个盒子的大小就是b(t)。在康托尔集合的例子中，这个盒子就是一维线段上的小区间，直线段的长度就是盒子尺寸b(t)，也就是3^-t。

这样，每个小盒子都能计算出一个α值，那么当我们给定了一个α以后，能够数出来一共有多少个小盒子与之对应。这个数等价于前面讨论的N，只不过，在这里我们计算的不是具有相同的质量m_i的小盒子的个数，而是具有相同的α，即质量随精度变化速度相同的小盒子个数。当t给定的时候，这两种描述实际上是等价的。于是，我们定义多重分形谱为：

[math]\displaystyle{ f(\alpha)=-\frac{\log(N(\alpha))}{\log(b(t))} }[/math]

其中N(α)就表示质量变化速度位于区间[α,α+dα]之中的小区间个数。如果大家熟悉分形，以及计算分形维中的盒计数法的话，就会发现，实际上这个f(α)就是分形集合：“所有那些具有相同α的小盒子的集合”的分形维。

直观理解

于是，我们的图景一下子就清楚了，实际上所谓的多重分形谱，就是描述一个崎岖地形的数学工具。其中，地形的高度就对应着质量的分布，质量越多的地方，高度越高。这种地形很怪异，因为它会随着观察尺度越来越精细而越来越坑洼不平。如果采用不同的盒子来划分水平面，从而把一个盒子中的山脉地形中的所有高度加总形成了粗粒化的新的高度，那么随着盒子越来越小，这种粗粒化的地形就会越来越颠簸。我们的描述手段就相当于：在一个观察精度下，用不同的水平面去截取这个地形，形成一些等高线，那么等高线所包围的区域就构成了一个分形，于是我们可以计算出它的分形维度。这样，该分形维如何随着α，即等高线高度对数与观测尺度对数的比值，而变化就够成了多重分形谱。

那么，这个多重分形谱的不同形状也就有了一定的解释。首先，如果这个地形是一个扁平的地形，也就是所有地点的高度都相同，那么多重分形谱就退化为一个点，这个点的横坐标是1，纵坐标是这个地形的支撑集合（即地形在XOY平面上的投影）的分形维。当地形稍微崎岖一点的时候，这个多重分形谱曲线就会具有一定的宽度。宽度越宽表示地形高度的取值越多样化。而多重分形谱曲线上的高度则对应了不同等高线所围分形集的维度，维度越大则表示分形集合的复杂程度越高，也就表示地形褶皱会比较多。

多重分形的数值计算

在上面的讨论中，我们针对康托尔集上的质量分布为例，引入了多重分形的定义。根据这个定义，原则上讲，我们也可以计算出多重分形谱来。只要计算每个观测尺度下α的数值，以及对应的f(α)就足够了。但是，这种计算往往会带来很大的误差，这主要是因为在此计算中，我们实际上是用单个盒子的质量分布来推测不同质量分布随着尺度而变的斜率这一整体信息。

下面介绍的方法不是从局部出发，而是从整体出发，计算出在不同观测精度下的Renyi信息维χ。其中，我们引入了一个新的参数q。在不同的参数q下，我们能够得到Renyi维随着观测精度变化的速率χ(q)。计算χ(q)可以按照最小二乘法拟合出log(S(q))对log(b(t))的斜率。之后，根据这个速度χ(q)和多重分形谱f(α)构成了勒让德变换（Legendre变换）对这一性质，我们就能估算出多重分形谱f(α)了。

Renyi信息维

我们首先要为多重分形定义一个新的量，叫做Renyi信息维度。对于一个多重分形场来说，当给定一个观测精度t，我们就得到了每一个小盒子b(t)中的质量分布m_i，其中要求[math]\displaystyle{ \sum_{i=1}^{n(t)}m_i=1 }[/math]，那么，对于这些m_i整体，我们可以计算如下的量:

[math]\displaystyle{ \chi_{t}(q)=\frac{\log(\sum_{i=1}^{n(t)}m_i^q)}{\log(b(t))} }[/math]

Renyi信息维就是这个量当t趋于无穷大时的极限，即定义为：

[math]\displaystyle{ \chi(q)=\lim_{t\rightarrow \infty}\chi_{t}(q)=\lim_{t\rightarrow \infty}\frac{\log(\sum_{i=1}^{n(t)}m_i^q)}{\log(b(t))} }[/math]

其中q是一个参数，可以取遍所有实数。n(t)是在t精度下所有小盒子的个数。这个Renyi信息维与分形维的定义十分相似，它计算的是广义的信息量[math]\displaystyle{ R(q)=\frac{1}{1-q}\sum_{i=1}^{n(t)}m_i^q }[/math]随着尺度增长的速度（参看Renyi信息熵）。当q=0的时候，求和式的结果就等于n(t)，于是这个维度χ(0)就退化成了多重分形的支撑集的分形维。当q=1的时候，这个量计算的是Shannon信息熵随尺度变化的速度。在实际的计算中，我们通过为待计算的集合划分不同精度的盒子，然后可以很容易地计算出[math]\displaystyle{ \sum_{i=1}^{n(t)}m_i^q }[/math]随log(b(t))的变化曲线，在对数坐标下，这条线变成了一条直线，于是我们可以计算出该直线的斜率，即为χ(q)。

我们说χ(q)反映的是多重分形场的整体信息，因为它对整个场的质量分布进行求和。 q的作用相当于一种权重，如果q>0，则那些质量大的小盒子就会对χ的贡献越大，从而χ就反映出来那些质量密集区域随着尺度变化信息量的增长速度。反过来若q<0，则m_i越小的区域会对整体的χ贡献越大，于是χ反映的就是质量小区域的信息量增长速度。

Legendre变换

有趣的是，χ(q)和f(α)存在着天然的联系。让我们来做一定的推演。首先，在给定精度t下，根据χ_t(q)的定义：

[math]\displaystyle{ \chi_{t}(q)=\frac{\log(\sum_{i=1}^{n(t)}m_i^q)}{\log(b(t))} }[/math]

其中n(t)表示t精度下小盒子的个数。在这些盒子中，有很多盒子具有相同的质量，即对于每个m_i都有N(m_i)个小盒子，这就意味着上式中的和式可以写为：

[math]\displaystyle{ \sum_{i=1}^{n(t)}m_i^q=\sum_{m_i}{N(m_i)m_i^q} }[/math]

也就是说，我们可以把对不同小盒子i的求和转换成对不同的盒子质量m_i的求和。而根据前面给出的α的定义，我们知道：

[math]\displaystyle{ m_i=(b(t))^{\alpha(t)} }[/math]

同样的道理，根据f(α)的定义：

[math]\displaystyle{ N(m_i)=(b(t))^{-f(\alpha(t))} }[/math]

于是，代到和式中：

[math]\displaystyle{ \sum_{i=1}^{n(t)}m_i^q=\sum_{\alpha(t)}{(b(t))^{-f(\alpha(t))+q \alpha(t)}} }[/math]

也就是说把求和下标又变成了α。当t趋于无穷大的时候，这个和式b(t)会远远小于1。于是求和号中的最小的那一项会起到最主要的贡献，以至于我们可以用下面的近似式：

[math]\displaystyle{ \sum_{i=1}^{n(t)}m_i^q=\sum_{\alpha(t)}{(b(t))^{-f(\alpha(t))+q \alpha(t)}}\approx b(t)^{\min_{\alpha}(q \alpha - f(\alpha)} }[/math]

这样，我们把求和号去掉了，相应地变成了使得等式[math]\displaystyle{ q \alpha -f(\alpha) }[/math]最小的那个α所对应项的值。把这些结果代入到Renyi维数的定义中就有：

[math]\displaystyle{ \chi(q)=\min_{\alpha}(q \alpha-f(\alpha)) }[/math]

这样，函数χ(q)和f(α)就构成了一个勒让德(Legendre)变换对。按照Legendre变换的性质，我们也可以根据函数χ(q)而反过来求出f(α)。

[math]\displaystyle{ f(\alpha)=\min_{q}(q \alpha-\chi(q)) }[/math]

于是，我们便可以通过全局的Renyi维度计算出多重分形谱f(α)。

在具体的计算中，我们当然可以针对一个α值，跑遍所有不同的q值，从而得到使得αq-χ(q)最小的一个q，从而计算出一个f(α)，但是这样计算起来过于繁琐。事实上，只要注意到，由于要让αq-χ(q)最小，我们是可以得到一个α关于最优的q的响应函数的α(q)。再把最优解代回去，又会得到f(α(q))，也就是说无论α还是f，实际上都是q的函数。这样，我们再让q跑遍所有的可能值，就会得到一组α(q)和f(q)的点对，把这一组点对画在α-f平面上就得到了我们要的多重分形谱。

而根据χ(q)的定义，我们实际上能够具体地写出α(q)和f(q)。我们知道最优的q要让αq-χ(q)最小。对q求导，得到α=χ'(q)。而根据定义，我们知道：

[math]\displaystyle{ \chi'(q)=\lim_{t\rightarrow \infty}\frac{(\log(\sum_{i}(m_i^q)))'}{\log(b(t))}=\lim_{t\rightarrow \infty}\frac{\sum_i{\frac{m_i^q}{\sum_im_i^q}\log(m_i)}}{\log(b(t))} }[/math]

这样，就得到了α(q)的表达式：

[math]\displaystyle{ \alpha(q)=\lim_{t\rightarrow \infty}\frac{1}{\log(b(t))}\sum_i{\mu_i \log(m_i)} }[/math]

其中，[math]\displaystyle{ \mu_i=m_i^q/\sum_i{m_i^q} }[/math]。这样，可以求出f(q)的表达式：

[math]\displaystyle{ f(q)=\lim_{t\rightarrow \infty}\frac{1}{\log(b(t))}\sum_i{\mu_i \log(\mu_i)} }[/math]

于是，就可以画出f(q)和α(q)的关系图了。

多重分形谱的计算

数学推导工作已经全部完成了。下面，我们就可以进行实实在在的计算了。我们不妨把多重分形谱的计算看作一个函数multifractal，它的输入是一个n*n矩阵M，代表一个二维的场，矩阵的每个元素代表对应场点的质量。当然至于更高维度的场也可以做类似的推广。那么multifractal计算需要如下几个步骤：

 (1).初始化，计算出n*n的空间总共能分成多少个方格盒子。一般地，我们设最小的盒子边长为2，最大的盒子边长为2int(log2n);
 (2). 对所有不同边长的盒子循环。
     (2.1). 对每个盒子，计算盒子内的总质量mij。
     (2.2). 将质量归一化，pij=mij/Σmij。
 (3). 对不同的q进行循环（通常我们事先给q一个预设的取值范围）
     (3.1).再次对所有边长的盒子（分辨率）循环
        (3.1.1) 计算在该分辨率下的A=Σμilog mi和B=μi log μi
     (3.2)根据不同分辨率下的A,B，对盒子大小b(t)在双对数坐标下做回归，计算出来α(q)和χ(q)
 (4). 输出α(q)和χ(q)的坐标组合，并画图。

下面，我们给出上述步骤在Matlab中的源代码实现，以供大家参考。

function MyMultiFractalSpectrum(data,dimension)
%原始数据可以是1维或者2维
%如果是2维,矩形区域,取最大的边为尺度,划分出一个正方形,作为场
   if dimension==2
       sizes=size(data);
       maxsz=max(sizes);
       %maxsz=min(sizes);
       field=zeros(maxsz,maxsz);
       field(1:sizes(1),1:sizes(2))=data;
   else
       field=data;
       maxsz=length(data);
   end
   
   maxboxsz=floor(log(maxsz)/log(2));
   massinmlevels={};
   probmlevels={};
   layer=4;
   
   %将场进行不同分辨率的划分,成为boxsz*boxsz的小区域，最后probmlevels是在不同分辨率下存储的各个小区域的总概率
   for layer=1:maxboxsz
       boxsz=2.^layer;
       coordinates=0:boxsz:maxsz-boxsz;
       if dimension==2
           [xx,yy]=meshgrid(coordinates);
           clusters=arrayfun(@(x,y){y+1:min(y+boxsz,maxsz),x+1:min(x+boxsz,maxsz)},yy,xx,'uniformoutput',false);
           clusters=clusters(:);
           bool=cell2mat(cellfun(@(x)(length(x{1})>0&length(x{2}>0)),clusters,'uniformoutput',false));
            clusters=clusters(bool);
           totalfields=cellfun(@(x)sum(sum(field(x{1},x{2}))),clusters,'uniformoutput',false);
           totalfields=cell2mat(totalfields);
       else
           clusters=arrayfun(@(x)x+1:min(x+boxsz,maxsz),coordinates,'uniformoutput',false);
           bool=cell2mat(cellfun(@(x)(length(x)>0),clusters,'uniformoutput',false));
           totalfields=cellfun(@(x)sum(field(x)),clusters,'uniformoutput',false);
           totalfields=cell2mat(totalfields);
       end
       massinmlevels={massinmlevels{:},totalfields};
       probmlevels={probmlevels{:},totalfields./sum(totalfields)};
   end
   
   %计算多重分形谱，alpha(q)和f(q)，qran为q的范围，qres为q的分辨率
   qran=10;qres=0.1;
   qq=-qran:qres:qran;
   fqss=[];
   alphaqss=[];
   q=-10+0.1;
   for q=qq
       fqs=[];
       alphaqs=[];
       for layer=1:maxboxsz
           bools=probmlevels{layer}>0;
           qmass=(probmlevels{layer}(bools)).^q;
           normalized=qmass./sum(qmass(~isinf(qmass)));
           fq=sum(normalized.*log(normalized));
           alphaq=sum(normalized.*log(probmlevels{layer}(bools)));
           fqs=[fqs,fq];
           alphaqs=[alphaqs,alphaq];
       end
       line1=polyfit(log(2.^(1:maxboxsz)),alphaqs,1);
       line2=polyfit(log(2.^(1:maxboxsz)),fqs,1);
       alphaqss=[alphaqss,line1(1)];
       fqss=[fqss,line2(1)];
   end
   %绘制多重分形谱的图
   figure;plot(qq,alphaqss,'r:o',qq,fqss,'g:o');
   h = legend('alpha(q)','f(q)',1); 
   xlabel('q','FontSize',14);
   figure;plot(alphaqss,fqss,'r:o');
   xlabel('alpha(q)','FontSize',14);
   ylabel('f(q)','FontSize',14);
end

多重分型谱应用举例

康托尔尘多重分形谱的计算

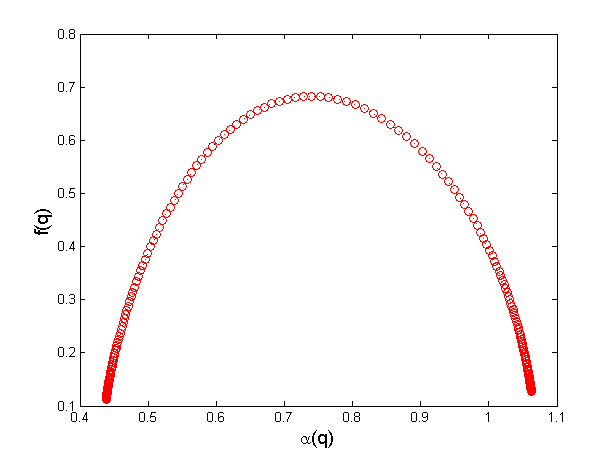
为了验证上述程序的正确性，我们对一维康托尔集多重分形进行了计算。首先，在计算机中生成了一个最高层数为9的康托集（即三分线段9次）。然后将这个一维的质量场输入上述程序中，计算出多重分形谱为：

我们看到，它与理论计算出的多重分形谱具有相似的形状。

数字图像

接下来，我们介绍A method for detecting objects using Legendre transform文章 中的结果。

该文章对比了自然景观和人造物的数字图像多重分形谱，发现自然景观的谱比人造物的谱更宽。于是，作者提议将数字图像划分成不同的子图像，从而利用每个子图像的多重分形谱的宽度，而找出自然景观背景下的人造物体。

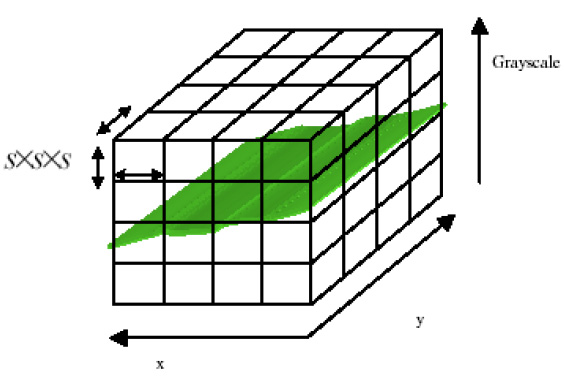
首先，作者指出，不能简单地计算三维空间z轴为灰度轴的多重分形谱，因为结果会对灰度的均值非常敏感。我们应先将数字图像转换成所谓的差分图像，然后再计算多重分形谱。具体地，假设原始图像的尺寸为M*M的，那么我们将图像分割成大小为S，（其中1<S<M/2）的三维盒子区域。如图所示：

现在我们考虑第(i,j)个三维的柱子，这里一共有M个立方体，有些立方体被灰度曲面占据了，有些立方体没有，我们设l为被灰度曲面占据的最高的立方体的下标，k为最矮的立方体的下标，计算：

[math]\displaystyle{ n(i,j)=l-k+1 }[/math]

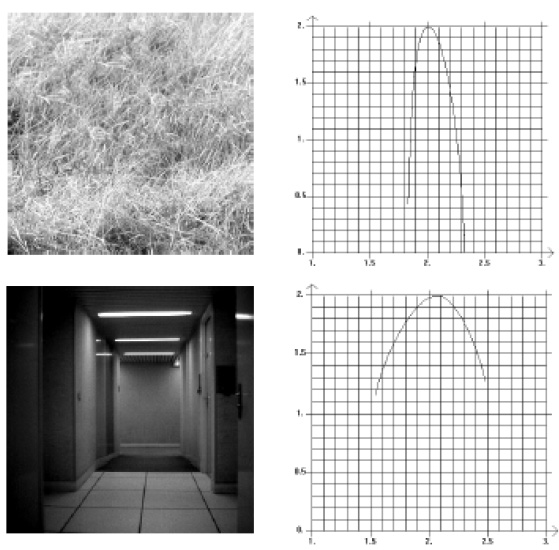
这样，我们就构造了一个地形（或场）n(i,j)，然后就可以按照上述方法来计算多重分形谱。下面的图展示了自然物体和人造物体对应二维数字图像的多重分形谱。我们可以看到自然图像的多重分形谱非常宽，而人工物体的谱则窄了很多。

回想一下，多重分形谱的宽度对应了场中数值的差异性程度。而我们研究的场并非灰度值本身，而是灰度的梯度（即变化率）。因此，自然图像的灰度梯度的差异性较均匀，而人工物体的灰度梯度的差异性分布则比较奇异。这样，我们便可以利用这个多重分形谱的宽度来辨别自然物或者人工物。

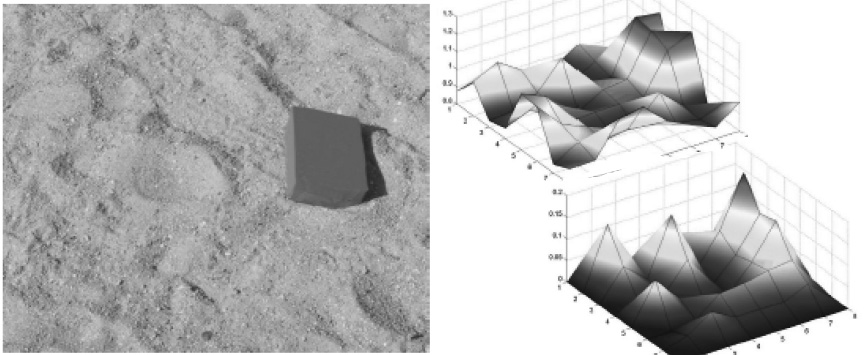
进一步，作者开发了一种在自然图像背景下辨识出人工物体的方法。他通过将一个数字图像划分成多个区域，分别对每个区域做出多重分形谱，通过寻找谱的宽度最大的区域来定位物体在哪一个区域。

右图的两个图形是作者定义的两种指标以反映子图形区块（X,Y坐标）多重分形谱的宽度。我们看到，人工物体所在的子图对应的宽度会更大。

参考文献

关于多重分形的教科书可以参考。多重分形在金融市场上的应用可以参考