“讨论:因果涌现”的版本间的差异
| 第23行: | 第23行: | ||
[[文件:动力学解耦例子2.png|居左|600x600像素|线性动力学解耦例子]] | [[文件:动力学解耦例子2.png|居左|600x600像素|线性动力学解耦例子]] | ||
| + | |||
| + | 下面展示一个具体的马尔科夫链的例子,其中系统的微观存在3个状态,转移矩阵如下图: | ||
| + | |||
| + | [[文件:批判例子.png|居左|600x500像素|不满足时间和空间可交换性例子]] | ||
| + | |||
| + | 其中,左侧的粗粒化矩阵A是 | ||
| + | |||
| + | <math> | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 & 0 \\ | ||
| + | 0 & 1 & 0 \\ | ||
| + | 0 & 0 & 1 | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | 它是一个恒等变换,而右侧的粗粒化矩阵A为: | ||
| + | |||
| + | <math> | ||
| + | \begin{pmatrix} | ||
| + | 1 & 1 & 0 \\ | ||
| + | 0 & 0 & 1 | ||
| + | \end{pmatrix} | ||
| + | </math> | ||
| + | |||
| + | 即将1、2两个状态分为一组,3状态单独一组。从图中,我们会发现该马尔科夫矩阵不满足公式{{EquationNote|3}}的可交换性条件。 | ||
2024年9月10日 (二) 13:51的最新版本
建议
- 因果涌现不一定限定在动力系统上,对于任何因果机制都应该可能存在着因果涌现现象
- 缺少一个对CE定义的公式
张老师应该在不同的模块写上对应的参考资料,让大家来共同整理
[math]\displaystyle{ {\overleftarrow{s}}'or {\overleftarrow{S}} }[/math]
<-'
s 符号含义
早期相关工作->计算力学,这部分,[math]\displaystyle{ {\overleftarrow{s}}' }[/math](表示[math]\displaystyle{ \overleftarrow{s} }[/math]的子集)[math]\displaystyle{ {\overleftarrow{s}}' }[/math]的含义,在Computational Mechanics文献中,[math]\displaystyle{ {\overleftarrow{s}}' }[/math]除了出现在因果态定义里,还出现在因果状态转换里,里面有“where by [math]\displaystyle{ {\overleftarrow{s}}' }[/math] we mean the history that is the immediate successor to [math]\displaystyle{ \overleftarrow{s} }[/math]; for consistency, [math]\displaystyle{ {\overleftarrow{s}}' = \overleftarrow{s}s }[/math].”
因此,作者的意思'可能表示S的子集(大写的s,即S)。
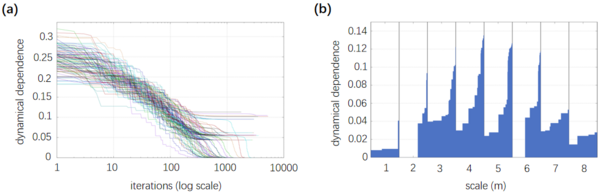
下图展示了一个线性动力系统的例子,其动力学是一个向量自回归的模型,实验结果如下所示,图a是使用遗传算法对不同的初始条件进行迭代进化的结果,纵轴表示动力学解耦的程度,横坐标代表迭代步数。从图中,我们可以看出:随着迭代的增加,动力学解耦程度也逐渐增加,图b表示不同的粗粒化尺度会影响优化到动力学解耦的程度,每个尺度下我们使用不同的初始化进行多次实验,结果按照升序排列,实验发现只有scale=2和6时可能达到动力学解耦,因此尺度的选择也很重要。
下面展示一个具体的马尔科夫链的例子,其中系统的微观存在3个状态,转移矩阵如下图:
其中,左侧的粗粒化矩阵A是
[math]\displaystyle{ \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} }[/math]
它是一个恒等变换,而右侧的粗粒化矩阵A为:
[math]\displaystyle{ \begin{pmatrix} 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} }[/math]
即将1、2两个状态分为一组,3状态单独一组。从图中,我们会发现该马尔科夫矩阵不满足公式3的可交换性条件。