“算术表达式”的版本间的差异
小 (→字串与语法树表示) |
小 |
||
| 第1行: | 第1行: | ||
| − | '''算术表达式'''是由[[数]]和[[算术运算]](也即四则运算)构成的[[表达式]]。算术表达式通常只是一个记录计算过程的符号串,它作为一个严密的数学对象本身的研究仍然是不充分的。对于一个复杂的数域,如实数域,记录一次计算过程本身写出一个表达式是容易的,然而作为一个概念,严格的定义实数域上的表达式仍然有内在的困难。这个困难之一来自于[[除零错误]]造成的[[语法]]与[[语义]]的不一致。另外一种困难来自于无限长度的表达式的计算,比如著名的令人迷惑的级数 <math> -\frac{1}{12}= 1 + 2 + 3 + ...</math> | + | '''算术表达式'''是由[[数]]和[[算术运算]](也即四则运算)构成的[[表达式]]。算术表达式通常只是一个记录计算过程的符号串,它作为一个严密的数学对象本身的研究仍然是不充分的。对于一个复杂的数域,如实数域,记录一次计算过程本身写出一个表达式是容易的,然而作为一个概念,严格的定义实数域上的表达式仍然有内在的困难。这个困难之一来自于[[除零错误]]造成的[[语法]]与[[语义]]的不一致。另外一种困难来自于无限长度的表达式的计算,比如著名的令人迷惑的级数 <math> -\frac{1}{12}= 1 + 2 + 3 + ...</math>。 |
== 语法式定义 == | == 语法式定义 == | ||
| 第27行: | 第27行: | ||
[[File:syntax-tree.png|300px|center]] | [[File:syntax-tree.png|300px|center]] | ||
| − | 严格地讲,如果我们把产生式的目标解读为字串,产生式规则对应字串拼接,我们就得到了'''字串表示''' | + | 严格地讲,如果我们把产生式的目标解读为字串,产生式规则对应字串拼接,我们就得到了'''字串表示''';如果目标是一个树,产生式规则解读为两个子树拼接成一个更大的树,那么我们就得到了'''语法树表示'''。我们可以很容易的通过前序遍历从语法树表示得到字串表示。 |
| − | + | 由语法树表示,我们很容易的从子树引入'''子表达式'''的概念;树的内部节点对应操作符 +、−、×、÷ ,而叶节点对应数字。 | |
== 表达式的估值 == | == 表达式的估值 == | ||
| + | |||
| + | |||
| + | |||
| + | ==参考文献== | ||
| + | |||
| + | 本节的内容主要来自苑明理的[https://github.com/mountain/aeg-paper 研究手稿]。 | ||
2024年12月29日 (日) 13:13的版本
算术表达式是由数和算术运算(也即四则运算)构成的表达式。算术表达式通常只是一个记录计算过程的符号串,它作为一个严密的数学对象本身的研究仍然是不充分的。对于一个复杂的数域,如实数域,记录一次计算过程本身写出一个表达式是容易的,然而作为一个概念,严格的定义实数域上的表达式仍然有内在的困难。这个困难之一来自于除零错误造成的语法与语义的不一致。另外一种困难来自于无限长度的表达式的计算,比如著名的令人迷惑的级数 [math]\displaystyle{ -\frac{1}{12}= 1 + 2 + 3 + ... }[/math]。
语法式定义
下面我们形式的引入有理数域上的算术表达式,因为此时我们可以存在算法判定如下的纯语法式构造什么时候会出现除零错误。
有理数域[math]\displaystyle{ \mathbb{Q} }[/math]上的算术表达式是指由如下产生式规则生成的符号串
- [math]\displaystyle{ a \longleftarrow x }[/math]
- [math]\displaystyle{ a \longleftarrow ( a + a ) }[/math]
- [math]\displaystyle{ a \longleftarrow ( a - a ) }[/math]
- [math]\displaystyle{ a \longleftarrow ( a \times a ) }[/math]
- [math]\displaystyle{ a \longleftarrow ( a \div a ) }[/math]
其中 [math]\displaystyle{ x \in \mathbb{Q} }[/math],我们称此时有 [math]\displaystyle{ a \in \mathbb{E} \left [\mathbb{Q} \right ] }[/math]。
字串与语法树表示
在上述生成过程中,我们可以得到一个算术表达式的字串表示或者树表示,两种表示是等价的。例如:
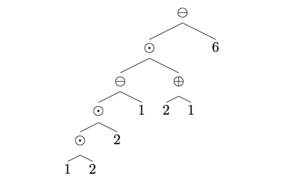
[math]\displaystyle{ (((((1 \times 2) \times 2) - 1) \times (2 + 1)) - 6)\label{eq:equation} }[/math]
相应的语法树如下:
严格地讲,如果我们把产生式的目标解读为字串,产生式规则对应字串拼接,我们就得到了字串表示;如果目标是一个树,产生式规则解读为两个子树拼接成一个更大的树,那么我们就得到了语法树表示。我们可以很容易的通过前序遍历从语法树表示得到字串表示。
由语法树表示,我们很容易的从子树引入子表达式的概念;树的内部节点对应操作符 +、−、×、÷ ,而叶节点对应数字。
表达式的估值
参考文献
本节的内容主要来自苑明理的研究手稿。