“朗顿的蚂蚁”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第4行： 第4行：
 
}}
 
}}
  
−
'''朗顿蚂蚁'''（Langton's ant）是[[元胞自动机]]的例子。它由[[克里斯托弗·朗顿 Christopher Langton]]在1986年提出，它由黑白格子和一只“蚂蚁”构成<ref >C.G.Langton (1986) [https://pattern.swarma.org/paper?id=074d27dc-5386-11ea-be1d-0242ac1a0005 Studying artificial life with cellular automata].Physica D.22.1-3:(120-149)</ref>，是一个二维图灵机。朗顿蚂蚁拥有非常简单的逻辑和复杂的表现。在2000年朗顿蚂蚁的图灵完备性被证明。朗顿蚂蚁的想法后来被推广，比如使用多种颜色和状态。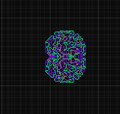[[File:蚂蚁图像.png | right| thumb | 11000步后的朗顿蚂蚁图像，红色像素是蚂蚁所在的位置。]]
+
'''朗顿蚂蚁 Langton's ant'''是[[元胞自动机 Cellular Automata]]的例子。它由[[克里斯托弗·朗顿 Christopher Langton]]在1986年提出，它由黑白格子和一只“蚂蚁”构成<ref >C.G.Langton (1986) [https://pattern.swarma.org/paper?id=074d27dc-5386-11ea-be1d-0242ac1a0005 Studying artificial life with cellular automata].Physica D.22.1-3:(120-149)</ref>，是一个二维图灵机。朗顿蚂蚁拥有非常简单的逻辑和复杂的表现。在2000年朗顿蚂蚁的图灵完备性被证明。朗顿蚂蚁的想法后来被推广，比如使用多种颜色和状态。[[File:蚂蚁图像.png | right| thumb | 11000步后的朗顿蚂蚁图像，红色像素是蚂蚁所在的位置。]]
  
 
== 规则==
 
== 规则==
第117行： 第117行：
  
 
*来自CSDN上的一篇博文[https://blog.csdn.net/u011488028/article/details/49643135? 蓝桥杯之兰顿蚂蚁- CSDN博客]
 
*来自CSDN上的一篇博文[https://blog.csdn.net/u011488028/article/details/49643135? 蓝桥杯之兰顿蚂蚁- CSDN博客]
−
*来自集智俱乐部的一篇微信公众号推文[https://swarma.org/?p=18576 什么是元胞自动机？]里面涉及到朗顿蚂蚁（Langton's ant）作为元胞自动机的例子。
 
  
−
----本中文词条由[[用户:Meng莫|Meng莫]]编辑，欢迎在讨论页面留言。
+
*来自集智俱乐部的一篇微信公众号推文[https://swarma.org/?p=18576 什么是元胞自动机？]
 +
::本文里涉及朗顿蚂蚁（Langton's ant）作为元胞自动机的例子。
 +
 
 +
*[https://pattern.swarma.org/paper?id=5e19d162-6e8b-11ea-b972-0242ac1a0005 Complexity of Langton's ant]
 +
::这篇文献中作者给出一个计算任何布尔电路与轨迹的一个单一蚂蚁。 通过对一维元胞自动机和图灵机的模拟，证明了系统的p-硬度 p-hardness，并揭示了蚂蚁的普遍性和与之相关的一些问题的不可判定性。
 +
 
 +
----本中文词条由[[用户:Meng莫|Meng莫]]和编辑，欢迎在讨论页面留言。
  
  
 
'''本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。'''
 
'''本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。'''

2020年4月24日 (五) 22:37的版本


朗顿蚂蚁 Langton's ant是元胞自动机 Cellular Automata的例子。它由克里斯托弗·朗顿 Christopher Langton在1986年提出，它由黑白格子和一只“蚂蚁”构成[1]，是一个二维图灵机。朗顿蚂蚁拥有非常简单的逻辑和复杂的表现。在2000年朗顿蚂蚁的图灵完备性被证明。朗顿蚂蚁的想法后来被推广，比如使用多种颜色和状态。

11000步后的朗顿蚂蚁图像，红色像素是蚂蚁所在的位置。

规则

前200步朗顿蚂蚁的动态图

在平面上的正方形格被填上黑色或白色。我们随意地把一个正方形定义为“蚂蚁”。它的头部朝向上下左右其中一方。“蚂蚁”按照下列规则行动：

  • 若蚂蚁在白格，右转90度，将该格改为黑格，向前移一步；
  • 若蚂蚁在黑格，左转90度，将该格改为白格，向前移一步。

朗顿的蚂蚁也可以被描述成一种细胞自动机，其中网格被涂成黑色或白色，“蚂蚁”所在的方块有八种不同颜色中的一种，它们被分配来编码黑/白状态的组合和蚂蚁当前的运动方向。[2]

行为模式

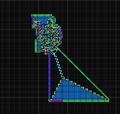
这些简单的规则会导致复杂的行为。从完全白色的网格开始时，三种明显的行为模式是显而易见的。

  1. 简单。在最初的几百次移动中，它创建了非常简单的模式，这些模式通常是对称的。
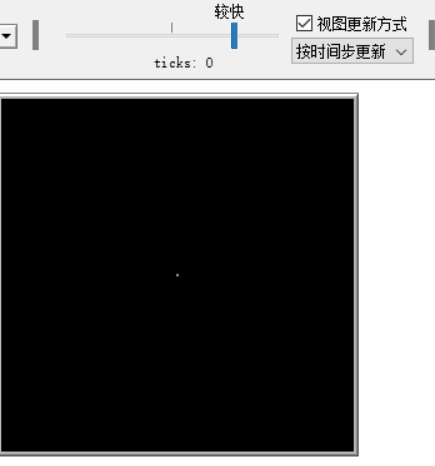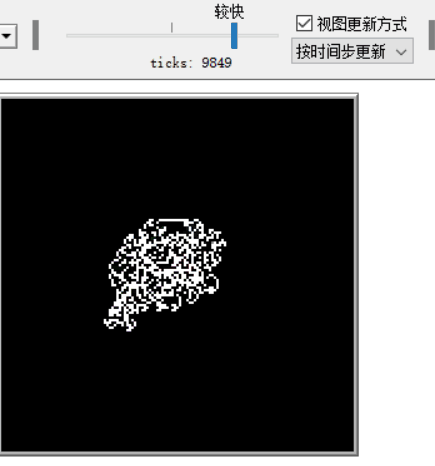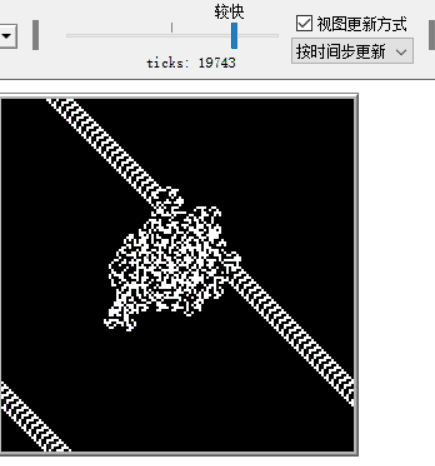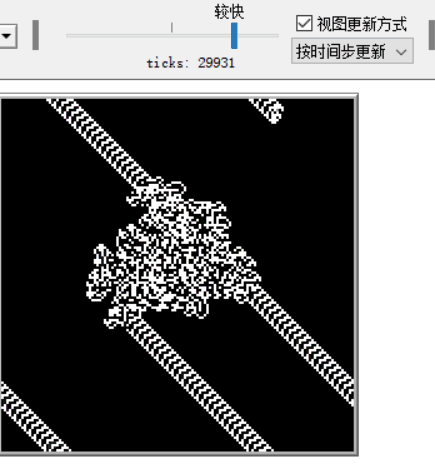
  2. 混乱。经过几百次移动，一个大的、不规则的黑白格子出现了。直到大约10,000步后，蚂蚁沿着一条伪随机路径直线行进。
  3. 突然出现的规则。最终，蚂蚁开始建立一个无限重复的104步循环“高速公路”模式。

若从全白的背景开始，在一开始的数百步，蚂蚁留下的路线会出现许多对称或重复的形状，然后会出现类似混沌的假随机，大至约一万步后会出现以104步为周期无限重复的“高速公路”朝固定方向移动[3]。在目前试过的所有起始状态，蚂蚁的路线最终都会变成高速公路，但尚无法证明这是无论任何起始状态都会导致的必然结果[4]。

代码部分即为该行为的演示。

NetLogo代码实现

源代码

to setup
  clear-all
  create-turtles 1[
    set heading random 1 * 90
  ]
  reset-ticks
end

to go
  ask turtles[
    ifelse pcolor = white[
      right 90
      set pcolor black
      forward 1
    ][
      left 90
      set pcolor  white
      forward 1
    ]
  ]
  tick
end

运行演示

代码演示界面

普遍性

在2000年，Gajardo等人展示了一种使用朗顿蚂蚁的单个实例的轨迹来计算任何布尔电路的构造，此外，还可以使用该蚂蚁的轨迹来模拟任意图灵机进行计算。 这意味着该蚂蚁具有通用计算能力。

推广到多种颜色

Greg Turk 和 Jim Propp 考虑一个关于朗顿蚂蚁的简单的扩展，除了两种颜色分别让蚂蚁左转或右转，也可以定义更多种颜色进行循环。通用的表示方法是用L和R依序表示各颜色是左转还是右转，朗顿蚂蚁的规则即可表示为RL。有些规则会产生对称或重复的形状。 这些扩展的朗顿蚂蚁中的一些产生的图案一次又一次变得对称。一个最简单的例子就是ant“RLLR”。这种情况发生的一个充分条件是，将蚂蚁的名字看作一个循环列表，它由连续对相同的字母“LL”或“RR”组成。(术语“循环列表”表明最后一个字母与第一个字母配对)这个证明涉及到Truchet tiles。

  • RLR: 混沌的生长，没有证实会产生高速公路

  • LLRR: 对称的生长

  • LRRRRRLLR: 形成方块

  • LLRRRLRLRLLR: 生成高速公路

  • RRLLLRLLLRRR: 生成一个移动并生长的实心三角形

  • L2NNL1L2L1: 六边形循环生长

  • L1L2NUL2L1R2: 六边形螺旋生长

六边形网格允许多达六种不同的旋转，这里记录为n(没有变化)，R1(60顺时针方向)，R2(120顺时针方向)，U(180)，L2(120逆时针方向)，L1(60逆时针方向)。

扩展到多种状态

朗顿蚂蚁的进一步扩展是考虑Turing机器的多种状态——就好像蚂蚁本身的颜色可以改变。 这些蚂蚁被称为“ Turmites”，即“ Turing machine ant”的缩写。 常见行为包括产生高速公路，混乱增长和螺旋增长。

  • 螺旋增长

  • 半混乱增长

  • 经过一段时间的混乱增长后的高速公路

  • 具有独特的纹理的混沌生长

  • 在扩大的框架内具有独特纹理的增长

  • 构造斐波那契螺旋

扩展到多只蚂蚁

多只朗顿的蚂蚁可以共存于2D平面上，它们的相互作用产生了复杂的高阶自动机，这些自动机共同构建了多种有组织的结构。我们不需要需解决冲突，因为坐在格上的每个蚂蚁都希望对黑白盘进行相同的更改。通过这个视频可以看到这些。 只需要制定一个规则，当它们相遇时，多个turmits就可以共存于2D平面上。Ed Pegg, Jr.认为当他们相遇时，可以制定一分为二或互相消灭的规则。

参考文献

  1. ↑ C.G.Langton (1986) Studying artificial life with cellular automata.Physica D.22.1-3:(120-149)
  2. ↑ Gajardo, A., Moreira, A., Goles, E. (2002) "Complexity of Langton's ant.(15 March, Discrete Applied Mathematics.117, 10.(41--50, S0166, 00334--6)
  3. ↑ Pratchett (1999) The Science Of Discworld.
  4. ↑ Bunimovich (1992) Recurrence properties of Lorentz lattice gas cellular automata.Journal of Statistical Physics.67, 10.(289--302)

外部链接

编者推荐

本文里涉及朗顿蚂蚁（Langton's ant）作为元胞自动机的例子。
这篇文献中作者给出一个计算任何布尔电路与轨迹的一个单一蚂蚁。 通过对一维元胞自动机和图灵机的模拟，证明了系统的p-硬度 p-hardness，并揭示了蚂蚁的普遍性和与之相关的一些问题的不可判定性。

本中文词条由Meng莫和编辑，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=朗顿的蚂蚁&oldid=5257”