“网络模体”的版本间的差异
| 第729行: | 第729行: | ||
| − | + | 大多数模体功能分析是基于模体孤立运行的情形。最近的研究<ref>{{cite journal |vauthors=Knabe JF, Nehaniv CL, Schilstra MJ |title=Do motifs reflect evolved function?—No convergent evolution of genetic regulatory network subgraph topologies |journal=BioSystems |volume=94 |issue=1–2 |pages=68–74 |year=2008 |pmid=18611431 |doi=10.1016/j.biosystems.2008.05.012 }}</ref>表明网络环境至关重要,不能忽视网络环境而仅从本地结构来对其功能进行推论——引用的论文还回顾了对观测数据的批判及其他可能的解释。人们研究了单个模体模组对网络全局的动力学影响及其分析<ref>{{cite journal |vauthors=Taylor D, Restrepo JG |title=Network connectivity during mergers and growth: Optimizing the addition of a module |journal=Physical Review E |volume=83 |issue=6 |year=2011 |page=66112 |doi=10.1103/PhysRevE.83.066112 |pmid=21797446 |bibcode=2011PhRvE..83f6112T |arxiv=1102.4876 }}</ref>。而另一项近期的研究工作提出生物网络的某些拓扑特征自然地引起经典模体的常见形态,让人不禁疑问:发生频率是否能证明模体的结构是出于其对所在网络运行的功能性贡献而被保留下的结果?<ref>{{cite journal|last1=Konagurthu|first1=Arun S.|last2=Lesk|first2=Arthur M.|title=Single and multiple input modules in regulatory networks|journal=Proteins: Structure, Function, and Bioinformatics|date=23 April 2008|volume=73|issue=2|pages=320–324|doi=10.1002/prot.22053|pmid=18433061}}</ref><ref>{{cite journal |vauthors=Konagurthu AS, Lesk AM |title=On the origin of distribution patterns of motifs in biological networks |journal=BMC Syst Biol |volume=2 |pages=73 |year=2008 |pmid=18700017 |pmc=2538512 |doi=10.1186/1752-0509-2-73 }} {{open access}}</ref> | |
| 第736行: | 第736行: | ||
| − | + | 模体的研究主要应用于静态复杂网络,而时变复杂网络的研究<ref>Braha, D., & Bar‐Yam, Y. (2006). [https://static1.squarespace.com/static/5b68a4e4a2772c2a206180a1/t/5c5de3faf4e1fc43e7b3d21e/1549657083988/Complexity_Braha_Original_w_Cover.pdf From centrality to temporary fame: Dynamic centrality in complex networks]. Complexity, 12(2), 59-63. </ref>对网络模体的提出了重大的新解释,并介绍了时变网络模体的概念。Braha和Bar-Yam<ref> Braha D., Bar-Yam Y. (2009) [https://s3.amazonaws.com/academia.edu.documents/4892116/Adaptive_Networks__Theory__Models_and_Applications__Understanding_Complex_Systems_.pdf?response-content-disposition=inline%3B%20filename%3DRedes_teoria.pdf&X-Amz-Algorithm=AWS4-HMAC-SHA256&X-Amz-Credential=AKIAIWOWYYGZ2Y53UL3A%2F20191111%2Fus-east-1%2Fs3%2Faws4_request&X-Amz-Date=20191111T173250Z&X-Amz-Expires=3600&X-Amz-SignedHeaders=host&X-Amz-Signature=89d08c9e92b88ed817e4eb0f87c480757ef79c4b865919a5e0890cbefa164c61#page=55 Time-Dependent Complex Networks: Dynamic Centrality, Dynamic Motifs, and Cycles of Social Interactions]. In: Gross T., Sayama H. (eds) Adaptive Networks. Understanding Complex Systems. Springer, Berlin, Heidelberg </ref>研究了 | |
本地模体结构在时间依赖网络/时变网络的动力学,发现的一些反复模式有望成为社会互动周期的经验论据。他们证明了对于时变网络,其本地结构是时间依赖的且可能随时间演变,作为对复杂网络中稳定模体观及的模体表达观的反论,Braha和Bar-Yam进一步提出,时变本地结构的分析可能提供关于系统级任务和功能的动力信息重要信息。 | 本地模体结构在时间依赖网络/时变网络的动力学,发现的一些反复模式有望成为社会互动周期的经验论据。他们证明了对于时变网络,其本地结构是时间依赖的且可能随时间演变,作为对复杂网络中稳定模体观及的模体表达观的反论,Braha和Bar-Yam进一步提出,时变本地结构的分析可能提供关于系统级任务和功能的动力信息重要信息。 | ||
2020年5月7日 (四) 00:08的版本
大家好,我们的公众号计划要推送一篇关于网络模体的综述文章,我们希望可以配套建议该重要概念:网络模体。现在希望可以大家一起协作完成这个词条。 翻译任务主要分为以下5个内容:
- 网络定义和历史 ---许菁
- 网络模体的发现算法 mfinder和FPF算法---李鹏
- 网络模体的发现算法 G-Trie、算法对比和算法分类——Ricky(中英对照初稿在这里)
- 已有网络模体及其函数表示 --周佳欣
- 活动模体+批判 --- 孙宇
- 代码实现
大家可以在对应感兴趣的部分下面,写上姓名。我们的协作方式是石墨文档上翻译,最后再编辑成文。 对应的词条链接:https://en.wikipedia.org/wiki/Network_motif#Well-established_motifs_and_their_functions
截止时间:今晚12:00
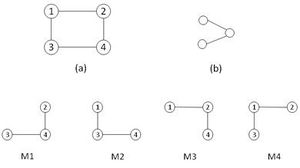
All networks, including biological networks, social networks, technological networks (e.g., computer networks and electrical circuits) and more, can be represented as graphs, which include a wide variety of subgraphs. One important local property of networks are so-called network motifs, which are defined as recurrent and statistically significant sub-graphs or patterns.
所有网络,包括生物网络(biological networks)、社会网络(social networks)、技术网络(例如计算机网络和电路)等,都可以用图的形式来表示,这些图中会包括各种各样的子图(subgraphs)。网络的一个重要的局部性质是所谓的网络基序,即重复且具有统计意义的子图或模式(patterns)。
Network motifs are sub-graphs that repeat themselves in a specific network or even among various networks. Each of these sub-graphs, defined by a particular pattern of interactions between vertices, may reflect a framework in which particular functions are achieved efficiently. Indeed, motifs are of notable importance largely because they may reflect functional properties. They have recently gathered much attention as a useful concept to uncover structural design principles of complex networks.[1] Although network motifs may provide a deep insight into the network's functional abilities, their detection is computationally challenging. 网络模体(Network motifs)是指在特定网络或各种网络中重复出现的相同的子图。这些子图由顶点之间特定的交互模式定义,一个子图便可以反映一个框架,这个框架可以有效地实现某个特定的功能。事实上,之所以说模体是一个重要的特性,正是因为它们可能反映出对应网络功能的这一性质。近年来这一概念作为揭示复杂网络结构设计原理的一个有用概念而受到了广泛的关注。[1] 但是,虽然通过研究网络模体可以深入了解网络的功能,但是对于模体的检测在计算上是具有挑战性的。
Definition
Let G = (V, E) and G′ = (V′, E′) be two graphs. Graph G′ is a sub-graph of graph G (written as G′ ⊆ G) if V′ ⊆ V and E′ ⊆ E ∩ (V′ × V′). If G′ ⊆ G and G′ contains all of the edges 〈u, v〉 ∈ E with u, v ∈ V′, then G′ is an induced sub-graph of G. We call G′ and G isomorphic (written as G′ ↔ G), if there exists a bijection (one-to-one) f:V′ → V with 〈u, v〉 ∈ E′ ⇔ 〈f(u), f(v)〉 ∈ E for all u, v ∈ V′. The mapping f is called an isomorphism between G and G′.[2]
设G = (V, E) 和 G′ = (V′, E′) 是两个图。若V′ ⊆ V且满足E′ ⊆ E ∩ (V′ × V′))(即图{{math|G′ ⊆ G}的所有边和点都属于图G)则称图{{math|G′ ⊆ G}是图G的一个子图[2]
若G′ ⊆ G,且对于顶点u、v及其连边,只要u和v存在于G′(即若U, V′ ⊆ V),那么G′ ⊆ G中就应该包含原图G中的所有u和V的对应连边(即〈u, v〉 ∈ E),则称此时图G′就是图G的导出子图。
如果存在一个双射(一对一)f:V′ → V,且对所有u, v ∈ V′都有〈u, v〉 ∈ E′ ⇔ 〈f(u), f(v)〉 ∈ E ,则称G&prime 是G的同构图(记作:G′ → G),映射f则称为G与G′之间的同构(isomorphism)。[2]
When G″ ⊂ G and there exists an isomorphism between the sub-graph G″ and a graph G′, this mapping represents an appearance of G′ in G. The number of appearances of graph G′ in G is called the frequency FG of G′ in G. A graph is called recurrent (or frequent) in G, when its frequency FG(G′) is above a predefined threshold or cut-off value. We use terms pattern and frequent sub-graph in this review interchangeably. There is an ensemble Ω(G) of random graphs corresponding to the null-model associated to G. We should choose N random graphs uniformly from Ω(G) and calculate the frequency for a particular frequent sub-graph G′ in G. If the frequency of G′ in G is higher than its arithmetic mean frequency in N random graphs Ri, where 1 ≤ i ≤ N, we call this recurrent pattern significant and hence treat G′ as a network motif for G. For a small graph G′, the network G and a set of randomized networks R(G) ⊆ Ω(R), where R(G) = N, the Z-Score that has been defined by the following formula:
[math]\displaystyle{ Z(G^\prime) = \frac{F_G(G^\prime) - \mu_R(G^\prime)}{\sigma_R(G^\prime)} }[/math]
当G″ ⊂ G,且G″与图G′之间存在同构时,该映射表示G′对于G存在。图G′在G的出现次数称为G′出现在G的频率FG。当一个子图的频率FG高于预定的阈值或截止值时,则称G′是G中的递归(或频繁)子图。
在接下来的内容中,我们交替使用术语“模式(motifs)”和“频繁子图(frequent sub-graph)”。
设从与G相关联的零模型(the null-model)获得的随机图集合为Ω(G),我们从Ω(G)中均匀地选择N个随机图,并计算其特定频繁子图的频率。如果G′出现在G的频率高于N个随机图Ri的算术平均频率,其中1 ≤ i ≤ N,我们称此递归模式是有意义的,因此可以将G′视为G的网络模体。
对于一个小图G′,网络G和一组随机网络R(G) ⊆ Ω(R),当R(G) = N时,由其Z分数(Z-score)的定义如下式:
[math]\displaystyle{ Z(G^\prime) = \frac{F_G(G^\prime) - \mu_R(G^\prime)}{\sigma_R(G^\prime)} }[/math]
where μR(G′) and σR(G′) stand for mean and standard deviation frequency in set R(G), respectively.[3][4][5][6][7][8] The larger the Z(G′), the more significant is the sub-graph G′ as a motif. Alternatively, another measurement in statistical hypothesis testing that can be considered in motif detection is the P-Value, given as the probability of FR(G′) ≥ FG(G′) (as its null-hypothesis), where FR(G′) indicates the frequency of G' in a randomized network.[6] A sub-graph with P-value less than a threshold (commonly 0.01 or 0.05) will be treated as a significant pattern. The P-value is defined as
[math]\displaystyle{ P(G^\prime) = \frac{1}{N}\sum_{i=1}^N \delta(c(i)) ; c(i): F_R^i(G^\prime) \ge F_G(G^\prime) }[/math]
式中,μR(G′) 和 σR(G′)分别代表集合R(G)中的平均和标准偏差频率。.[3][4][5][6][7][8] Z(G′)越大,子图G′作为模体的意义也就越大。
此外还可以使用统计假设检验中的另一个测量方法,可以作为模体检测中的一种方法,即P值(P-value),以 FR(G′) ≥ FG(G′)的概率给出(作为其零假设null-hypothesis),其中FR(G′)表示随机网络中G′的频率。[6] 当P值小于阈值(通常为0.01或0.05)时,该子图可以被称为显著模式。该P值定义为:
[math]\displaystyle{ P(G^\prime) = \frac{1}{N}\sum_{i=1}^N \delta(c(i)) ; c(i): F_R^i(G^\prime) \ge F_G(G^\prime) }[/math]
Where N indicates number of randomized networks, i is defined over an ensemble of randomized networks and the Kronecker delta function δ(c(i)) is one if the condition c(i) holds. The concentration [9][10] of a particular n-size sub-graph G′ in network G refers to the ratio of the sub-graph appearance in the network to the total n-size non-isomorphic sub-graphs’ frequencies, which is formulated by
[math]\displaystyle{ C_G(G^\prime) = \frac{F_G(G^\prime)}{\sum_i F_G(G_i)} }[/math]
where index i is defined over the set of all non-isomorphic n-size graphs. Another statistical measurement is defined for evaluating network motifs, but it is rarely used in known algorithms. This measurement is introduced by Picard et al. in 2008 and used the Poisson distribution, rather than the Gaussian normal distribution that is implicitly being used above.[11]
其中索引 i 定义在所有非同构 n 大小图的集合上。 另一种统计测量是用来评估网络主题的,但在已知的算法中很少使用。 这种测量方法是由 Picard 等人在2008年提出的,使用的是泊松分佈分布,而不是上面隐含使用的高斯正态分布。[11]其中N表示随机网络的数目,i定义在随机网络的集合上,若条件c(i)成立,则Kroneckerδ函数δ(c(i))是1。在网络G中,一个特定的n维子图N′的集中度是指子图在网络中出现频率与n维非同构子图的总频率之比,其计算公式如下:
[math]\displaystyle{ C_G(G^\prime) = \frac{F_G(G^\prime)}{\sum_i F_G(G_i)} }[/math]
In addition, three specific concepts of sub-graph frequency have been proposed.[12] As the figure illustrates, the first frequency concept F1 considers all matches of a graph in original network. This definition is similar to what we have introduced above. The second concept F2 is defined as the maximum number of edge-disjoint instances of a given graph in original network. And finally, the frequency concept F3 entails matches with disjoint edges and nodes. Therefore, the two concepts F2 and F3 restrict the usage of elements of the graph, and as can be inferred, the frequency of a sub-graph declines by imposing restrictions on network element usage. As a result, a network motif detection algorithm would pass over more candidate sub-graphs if we insist on frequency concepts F2 and F3.
此外,他们还提出了子图频率的三个具体概念。[12] 如图所示,第一频率概念 F1考虑原始网络中图的所有匹配,这与我们前面介绍过的类似。第二个概念F2定义为原始网络中给定图的最大不相交边的数量。最后,频率概念F3包含与不相交边(disjoint edges)和节点的匹配。因此,两个概念F2和F3限制了图元素的使用,并且可以看出,通过对网络元素的使用施加限制,子图的频率下降。因此,如果我们坚持使用频率概念F2和F3,网络模体检测算法将可以筛选出更多的候选子图。
History
The study of network motifs was pioneered by Holland and Leinhardt[13][14][15][16] who introduced the concept of a triad census of networks. They introduced methods to enumerate various types of subgraph configurations, and test whether the subgraph counts are statistically different from those expected in random networks. 霍兰(Holland)和莱因哈特(Leinhardt)率先提出了网络三合会普查(a triad census of networks)的概念,开创了网络模体研究的先河。[17][18][19][20] 他们介绍了枚举各种子图配置的方法,并测试子图计数是否与随机网络中的期望值存在统计学上的差异。
这里对于网络三合会普查(a triad census of networks)这一概念的翻译存疑
This idea was further generalized in 2002 by Uri Alon and his group [21] when network motifs were discovered in the gene regulation (transcription) network of the bacteria E. coli and then in a large set of natural networks. Since then, a considerable number of studies have been conducted on the subject. Some of these studies focus on the biological applications, while others focus on the computational theory of network motifs.
2002年,Uri Alon和他的团队[17]在大肠杆菌的基因调控(gene regulation network)(转录 transcription)网络中发现了网络模体,随后在大量的自然网络中也发现了网络模体,从而进一步推广了这一观点。自那时起,许多科学家都对这一问题进行了大量的研究。其中一些研究集中在生物学应用上,而另一些则集中在网络模体的计算理论上。[21]
The biological studies endeavor to interpret the motifs detected for biological networks. For example, in work following,[21] the network motifs found in E. coli were discovered in the transcription networks of other bacteria[22] as well as yeast[23][24] and higher organisms.[25][26][27] A distinct set of network motifs were identified in other types of biological networks such as neuronal networks and protein interaction networks.[5][28][29]
生物学研究试图解释为生物网络检测到的模体。例如,在接下来的工作中,文献[17]在大肠杆菌中发现的网络模体存在于其他细菌[22]以及酵母[23][24]和高等生物的转录网络中。文献[25][26][27]在其他类型的生物网络中发现了一组不同的网络模体,如神经元网络和蛋白质相互作用网络。[5][28][29]
The computational research has focused on improving existing motif detection tools to assist the biological investigations and allow larger networks to be analyzed. Several different algorithms have been provided so far, which are elaborated in the next section in chronological order.
另一方面,对于计算研究的重点则是改进现有的模体检测工具,以协助生物学研究,并允许对更大的网络进行分析。到目前为止,已经提供了几种不同的算法,这些算法将在下一节按时间顺序进行阐述。
Most recently, the acc-MOTIF tool to detect network motifs was released.[30]
最近,还发布了用于检测网络基序的acc基序工具。[31]
Motif discovery algorithms
Various solutions have been proposed for the challenging problem of motif discovery. These algorithms can be classified under various paradigms such as exact counting methods, sampling methods, pattern growth methods and so on. However, motif discovery problem comprises two main steps: first, calculating the number of occurrences of a sub-graph and then, evaluating the sub-graph significance. The recurrence is significant if it is detectably far more than expected. Roughly speaking, the expected number of appearances of a sub-graph can be determined by a Null-model, which is defined by an ensemble of random networks with some of the same properties as the original network.
Here, a review on computational aspects of major algorithms is given and their related benefits and drawbacks from an algorithmic perspective are discussed.
mfinder
mfinder, the first motif-mining tool, implements two kinds of motif finding algorithms: a full enumeration and a sampling method. Until 2004, the only exact counting method for NM (network motif) detection was the brute-force one proposed by Milo et al..[3] This algorithm was successful for discovering small motifs, but using this method for finding even size 5 or 6 motifs was not computationally feasible. Hence, a new approach to this problem was needed.
Kashtan et al. [9] presented the first sampling NM discovery algorithm, which was based on edge sampling throughout the network. This algorithm estimates concentrations of induced sub-graphs and can be utilized for motif discovery in directed or undirected networks. The sampling procedure of the algorithm starts from an arbitrary edge of the network that leads to a sub-graph of size two, and then expands the sub-graph by choosing a random edge that is incident to the current sub-graph. After that, it continues choosing random neighboring edges until a sub-graph of size n is obtained. Finally, the sampled sub-graph is expanded to include all of the edges that exist in the network between these n nodes. When an algorithm uses a sampling approach, taking unbiased samples is the most important issue that the algorithm might address. The sampling procedure, however, does not take samples uniformly and therefore Kashtan et al. proposed a weighting scheme that assigns different weights to the different sub-graphs within network.[9] The underlying principle of weight allocation is exploiting the information of the sampling probability for each sub-graph, i.e. the probable sub-graphs will obtain comparatively less weights in comparison to the improbable sub-graphs; hence, the algorithm must calculate the sampling probability of each sub-graph that has been sampled. This weighting technique assists mfinder to determine sub-graph concentrations impartially.
In expanded to include sharp contrast to exhaustive search, the computational time of the algorithm surprisingly is asymptotically independent of the network size. An analysis of the computational time of the algorithm has shown that it takes O(nn) for each sample of a sub-graph of size n from the network. On the other hand, there is no analysis in [9] on the classification time of sampled sub-graphs that requires solving the graph isomorphism problem for each sub-graph sample. Additionally, an extra computational effort is imposed on the algorithm by the sub-graph weight calculation. But it is unavoidable to say that the algorithm may sample the same sub-graph multiple times – spending time without gathering any information.[10] In conclusion, by taking the advantages of sampling, the algorithm performs more efficiently than an exhaustive search algorithm; however, it only determines sub-graphs concentrations approximately. This algorithm can find motifs up to size 6 because of its main implementation, and as result it gives the most significant motif, not all the others too. Also, it is necessary to mention that this tool has no option of visual presentation. The sampling algorithm is shown briefly:
| mfinder |
|---|
| Definitions: Esis the set of picked edges. Vs is the set of all nodes that are touched by the edges in E. |
| Init Vs and Es to be empty sets.
1. Pick a random edge e1 = (vi, vj). Update Es = {e1}, Vs = {vi, vj} 2. Make a list L of all neighbor edges of Es. Omit from L all edges between members of Vs. 3. Pick a random edge e = {vk,vl} from L. Update Es = Es ⋃ {e}, Vs = Vs ⋃ {vk, vl}. 4. Repeat steps 2-3 until completing an n-node subgraph (until |Vs| = n). 5. Calculate the probability to sample the picked n-node subgraph. |
FPF (Mavisto)
Schreiber and Schwöbbermeyer [12] proposed an algorithm named flexible pattern finder (FPF) for extracting frequent sub-graphs of an input network and implemented it in a system named Mavisto.[32] Their algorithm exploits the downward closure property which is applicable for frequency concepts F2 and F3. The downward closure property asserts that the frequency for sub-graphs decrease monotonically by increasing the size of sub-graphs; however, this property does not hold necessarily for frequency concept F1. FPF is based on a pattern tree (see figure) consisting of nodes that represents different graphs (or patterns), where the parent of each node is a sub-graph of its children nodes; in other words, the corresponding graph of each pattern tree's node is expanded by adding a new edge to the graph of its parent node.
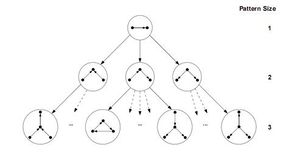
At first, the FPF algorithm enumerates and maintains the information of all matches of a sub-graph located at the root of the pattern tree. Then, one-by-one it builds child nodes of the previous node in the pattern tree by adding one edge supported by a matching edge in the target graph, and tries to expand all of the previous information about matches to the new sub-graph (child node). In next step, it decides whether the frequency of the current pattern is lower than a predefined threshold or not. If it is lower and if downward closure holds, FPF can abandon that path and not traverse further in this part of the tree; as a result, unnecessary computation is avoided. This procedure is continued until there is no remaining path to traverse.
The advantage of the algorithm is that it does not consider infrequent sub-graphs and tries to finish the enumeration process as soon as possible; therefore, it only spends time for promising nodes in the pattern tree and discards all other nodes. As an added bonus, the pattern tree notion permits FPF to be implemented and executed in a parallel manner since it is possible to traverse each path of the pattern tree independently. However, FPF is most useful for frequency concepts F2 and F3, because downward closure is not applicable to F1. Nevertheless, the pattern tree is still practical for F1 if the algorithm runs in parallel. Another advantage of the algorithm is that the implementation of this algorithm has no limitation on motif size, which makes it more amenable to improvements. The pseudocode of FPF (Mavisto) is shown below:
| Mavisto |
|---|
| Data: Graph G, target pattern size t, frequency concept F
Result: Set R of patterns of size t with maximum frequency. |
| R ← φ, fmax ← 0
P ←start pattern p1 of size 1 Mp1 ←all matches of p1 in G While P ≠ φ do Pmax ←select all patterns from P with maximum size. P ← select pattern with maximum frequency from Pmax Ε = ExtensionLoop(G, p, Mp) Foreach pattern p ∈ E If F = F1 then f ← size(Mp) Else f ← Maximum Independent set(F, Mp) End If size(p) = t then If f = fmax then R ← R ⋃ {p} Else if f > fmax then R ← {p}; fmax ← f End Else If F = F1 or f ≥ fmax then P ← P ⋃ {p} End End End End |
ESU (FANMOD)
The sampling bias of Kashtan et al. [9] provided great impetus for designing better algorithms for the NM discovery problem. Although Kashtan et al. tried to settle this drawback by means of a weighting scheme, this method imposed an undesired overhead on the running time as well a more complicated implementation. This tool is one of the most useful ones, as it supports visual options and also is an efficient algorithm with respect to time. But, it has a limitation on motif size as it does not allow searching for motifs of size 9 or higher because of the way the tool is implemented.
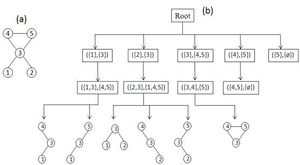
Wernicke [10] introduced an algorithm named RAND-ESU that provides a significant improvement over mfinder.[9] This algorithm, which is based on the exact enumeration algorithm ESU, has been implemented as an application called FANMOD.[10] RAND-ESU is a NM discovery algorithm applicable for both directed and undirected networks, effectively exploits an unbiased node sampling throughout the network, and prevents overcounting sub-graphs more than once. Furthermore, RAND-ESU uses a novel analytical approach called DIRECT for determining sub-graph significance instead of using an ensemble of random networks as a Null-model. The DIRECT method estimates the sub-graph concentration without explicitly generating random networks.[10] Empirically, the DIRECT method is more efficient in comparison with the random network ensemble in case of sub-graphs with a very low concentration; however, the classical Null-model is faster than the DIRECT method for highly concentrated sub-graphs.[3][10] In the following, we detail the ESU algorithm and then we show how this exact algorithm can be modified efficiently to RAND-ESU that estimates sub-graphs concentrations.
The algorithms ESU and RAND-ESU are fairly simple, and hence easy to implement. ESU first finds the set of all induced sub-graphs of size k, let Sk be this set. ESU can be implemented as a recursive function; the running of this function can be displayed as a tree-like structure of depth k, called the ESU-Tree (see figure). Each of the ESU-Tree nodes indicate the status of the recursive function that entails two consecutive sets SUB and EXT. SUB refers to nodes in the target network that are adjacent and establish a partial sub-graph of size |SUB| ≤ k. If |SUB| = k, the algorithm has found an induced complete sub-graph, so Sk = SUB ∪ Sk. However, if |SUB| < k, the algorithm must expand SUB to achieve cardinality k. This is done by the EXT set that contains all the nodes that satisfy two conditions: First, each of the nodes in EXT must be adjacent to at least one of the nodes in SUB; second, their numerical labels must be larger than the label of first element in SUB. The first condition makes sure that the expansion of SUB nodes yields a connected graph and the second condition causes ESU-Tree leaves (see figure) to be distinct; as a result, it prevents overcounting. Note that, the EXT set is not a static set, so in each step it may expand by some new nodes that do not breach the two conditions. The next step of ESU involves classification of sub-graphs placed in the ESU-Tree leaves into non-isomorphic size-k graph classes; consequently, ESU determines sub-graphs frequencies and concentrations. This stage has been implemented simply by employing McKay's nauty algorithm,[33][34] which classifies each sub-graph by performing a graph isomorphism test. Therefore, ESU finds the set of all induced k-size sub-graphs in a target graph by a recursive algorithm and then determines their frequency using an efficient tool.
The procedure of implementing RAND-ESU is quite straightforward and is one of the main advantages of FANMOD. One can change the ESU algorithm to explore just a portion of the ESU-Tree leaves by applying a probability value 0 ≤ pd ≤ 1 for each level of the ESU-Tree and oblige ESU to traverse each child node of a node in level d-1 with probability pd. This new algorithm is called RAND-ESU. Evidently, when pd = 1 for all levels, RAND-ESU acts like ESU. For pd = 0 the algorithm finds nothing. Note that, this procedure ensures that the chances of visiting each leaf of the ESU-Tree are the same, resulting in unbiased sampling of sub-graphs through the network. The probability of visiting each leaf is ∏dpd and this is identical for all of the ESU-Tree leaves; therefore, this method guarantees unbiased sampling of sub-graphs from the network. Nonetheless, determining the value of pd for 1 ≤ d ≤ k is another issue that must be determined manually by an expert to get precise results of sub-graph concentrations.[8] While there is no lucid prescript for this matter, the Wernicke provides some general observations that may help in determining p_d values. In summary, RAND-ESU is a very fast algorithm for NM discovery in the case of induced sub-graphs supporting unbiased sampling method. Although, the main ESU algorithm and so the FANMOD tool is known for discovering induced sub-graphs, there is trivial modification to ESU which makes it possible for finding non-induced sub-graphs, too. The pseudo code of ESU (FANMOD) is shown below:
| Enumeration of ESU (FANMOD) |
|---|
| EnumerateSubgraphs(G,k)
Input: A graph G = (V, E) and an integer 1 ≤ k ≤ |V|. Output: All size-k subgraphs in G. for each vertex v ∈ V do VExtension ← {u ∈ N({v}) | u > v} call ExtendSubgraph({v}, VExtension, v) endfor |
| ExtendSubgraph(VSubgraph, VExtension, v)
if |VSubgraph| = k then output G[VSubgraph] and return while VExtension ≠ ∅ do Remove an arbitrarily chosen vertex w from VExtension VExtension′ ← VExtension ∪ {u ∈ Nexcl(w, VSubgraph) | u > v} call ExtendSubgraph(VSubgraph ∪ {w}, VExtension′, v) return |
NeMoFinder
Chen et al. [35] introduced a new NM discovery algorithm called NeMoFinder, which adapts the idea in SPIN [36] to extract frequent trees and after that expands them into non-isomorphic graphs.[8] NeMoFinder utilizes frequent size-n trees to partition the input network into a collection of size-n graphs, afterward finding frequent size-n sub-graphs by expansion of frequent trees edge-by-edge until getting a complete size-n graph Kn. The algorithm finds NMs in undirected networks and is not limited to extracting only induced sub-graphs. Furthermore, NeMoFinder is an exact enumeration algorithm and is not based on a sampling method. As Chen et al. claim, NeMoFinder is applicable for detecting relatively large NMs, for instance, finding NMs up to size-12 from the whole S. cerevisiae (yeast) PPI network as the authors claimed.[37]
NeMoFinder consists of three main steps. First, finding frequent size-n trees, then utilizing repeated size-n trees to divide the entire network into a collection of size-n graphs, finally, performing sub-graph join operations to find frequent size-n sub-graphs.[35] In the first step, the algorithm detects all non-isomorphic size-n trees and mappings from a tree to the network. In the second step, the ranges of these mappings are employed to partition the network into size-n graphs. Up to this step, there is no distinction between NeMoFinder and an exact enumeration method. However, a large portion of non-isomorphic size-n graphs still remain. NeMoFinder exploits a heuristic to enumerate non-tree size-n graphs by the obtained information from the preceding steps. The main advantage of the algorithm is in the third step, which generates candidate sub-graphs from previously enumerated sub-graphs. This generation of new size-n sub-graphs is done by joining each previous sub-graph with derivative sub-graphs from itself called cousin sub-graphs. These new sub-graphs contain one additional edge in comparison to the previous sub-graphs. However, there exist some problems in generating new sub-graphs: There is no clear method to derive cousins from a graph, joining a sub-graph with its cousins leads to redundancy in generating particular sub-graph more than once, and cousin determination is done by a canonical representation of the adjacency matrix which is not closed under join operation. NeMoFinder is an efficient network motif finding algorithm for motifs up to size 12 only for protein-protein interaction networks, which are presented as undirected graphs. And it is not able to work on directed networks which are so important in the field of complex and biological networks. The pseudocode of NeMoFinder is shown below:
| NeMoFinder |
|---|
| Input:
G - PPI network; N - Number of randomized networks; K - Maximal network motif size; F - Frequency threshold; S - Uniqueness threshold; Output: U - Repeated and unique network motif set; D ← ∅; for motif-size k from 3 to K do T ← FindRepeatedTrees(k); GDk ← GraphPartition(G, T) D ← D ∪ T; D′ ← T; i ← k; while D′ ≠ ∅ and i ≤ k × (k - 1) / 2 do D′ ← FindRepeatedGraphs(k, i, D′); D ← D ∪ D′; i ← i + 1; end while end for for counter i from 1 to N do Grand ← RandomizedNetworkGeneration(); for each g ∈ D do GetRandFrequency(g, Grand); end for end for U ← ∅; for each g ∈ D do s ← GetUniqunessValue(g); if s ≥ S then U ← U ∪ {g}; end if end for return U; |
Grochow–Kellis
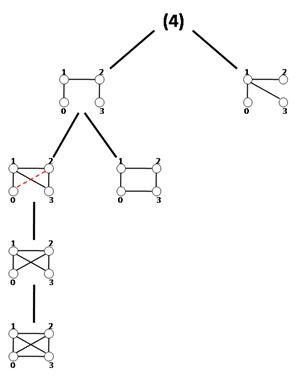
Grochow and Kellis [38] proposed an exact algorithm for enumerating sub-graph appearances. The algorithm is based on a motif-centric approach, which means that the frequency of a given sub-graph,called the query graph, is exhaustively determined by searching for all possible mappings from the query graph into the larger network. It is claimed [38] that a motif-centric method in comparison to network-centric methods has some beneficial features. First of all it avoids the increased complexity of sub-graph enumeration. Also, by using mapping instead of enumerating, it enables an improvement in the isomorphism test. To improve the performance of the algorithm, since it is an inefficient exact enumeration algorithm, the authors introduced a fast method which is called symmetry-breaking conditions. During straightforward sub-graph isomorphism tests, a sub-graph may be mapped to the same sub-graph of the query graph multiple times. In the Grochow–Kellis (GK) algorithm symmetry-breaking is used to avoid such multiple mappings. Here we introduce the GK algorithm and the symmetry-breaking condition which eliminates redundant isomorphism tests.
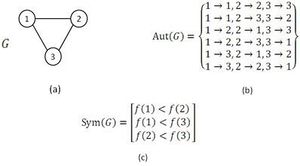
The GK algorithm discovers the whole set of mappings of a given query graph to the network in two major steps. It starts with the computation of symmetry-breaking conditions of the query graph. Next, by means of a branch-and-bound method, the algorithm tries to find every possible mapping from the query graph to the network that meets the associated symmetry-breaking conditions. An example of the usage of symmetry-breaking conditions in GK algorithm is demonstrated in figure.
As it is mentioned above, the symmetry-breaking technique is a simple mechanism that precludes spending time finding a sub-graph more than once due to its symmetries.[38][39] Note that, computing symmetry-breaking conditions requires finding all automorphisms of a given query graph. Even though, there is no efficient (or polynomial time) algorithm for the graph automorphism problem, this problem can be tackled efficiently in practice by McKay's tools.[33][34] As it is claimed, using symmetry-breaking conditions in NM detection lead to save a great deal of running time. Moreover, it can be inferred from the results in [38][39] that using the symmetry-breaking conditions results in high efficiency particularly for directed networks in comparison to undirected networks. The symmetry-breaking conditions used in the GK algorithm are similar to the restriction which ESU algorithm applies to the labels in EXT and SUB sets. In conclusion, the GK algorithm computes the exact number of appearance of a given query graph in a large complex network and exploiting symmetry-breaking conditions improves the algorithm performance. Also, GK algorithm is one of the known algorithms having no limitation for motif size in implementation and potentially it can find motifs of any size.
Color-coding approach
Most algorithms in the field of NM discovery are used to find induced sub-graphs of a network. In 2008, Noga Alon et al. [40] introduced an approach for finding non-induced sub-graphs too. Their technique works on undirected networks such as PPI ones. Also, it counts non-induced trees and bounded treewidth sub-graphs. This method is applied for sub-graphs of size up to 10.
This algorithm counts the number of non-induced occurrences of a tree T with k = O(logn) vertices in a network G with n vertices as follows:
- Color coding. Color each vertex of input network G independently and uniformly at random with one of the k colors.
- Counting. Apply a dynamic programming routine to count the number of non-induced occurrences of T in which each vertex has a unique color. For more details on this step, see.[40]
- Repeat the above two steps O(ek) times and add up the number of occurrences of T to get an estimate on the number of its occurrences in G.
As available PPI networks are far from complete and error free, this approach is suitable for NM discovery for such networks. As Grochow–Kellis Algorithm and this one are the ones popular for non-induced sub-graphs, it is worth to mention that the algorithm introduced by Alon et al. is less time-consuming than the Grochow–Kellis Algorithm.[40]
MODA
Omidi et al. [41] introduced a new algorithm for motif detection named MODA which is applicable for induced and non-induced NM discovery in undirected networks. It is based on the motif-centric approach discussed in the Grochow–Kellis algorithm section. It is very important to distinguish motif-centric algorithms such as MODA and GK algorithm because of their ability to work as query-finding algorithms. This feature allows such algorithms to be able to find a single motif query or a small number of motif queries (not all possible sub-graphs of a given size) with larger sizes. As the number of possible non-isomorphic sub-graphs increases exponentially with sub-graph size, for large size motifs (even larger than 10), the network-centric algorithms, those looking for all possible sub-graphs, face a problem. Although motif-centric algorithms also have problems in discovering all possible large size sub-graphs, but their ability to find small numbers of them is sometimes a significant property.
Using a hierarchical structure called an expansion tree, the MODA algorithm is able to extract NMs of a given size systematically and similar to FPF that avoids enumerating unpromising sub-graphs; MODA takes into consideration potential queries (or candidate sub-graphs) that would result in frequent sub-graphs. Despite the fact that MODA resembles FPF in using a tree like structure, the expansion tree is applicable merely for computing frequency concept F1. As we will discuss next, the advantage of this algorithm is that it does not carry out the sub-graph isomorphism test for non-tree query graphs. Additionally, it utilizes a sampling method in order to speed up the running time of the algorithm.
Here is the main idea: by a simple criterion one can generalize a mapping of a k-size graph into the network to its same size supergraphs. For example, suppose there is mapping f(G) of graph G with k nodes into the network and we have a same size graph G′ with one more edge &langu, v〉; fG will map G′ into the network, if there is an edge 〈fG(u), fG(v)〉 in the network. As a result, we can exploit the mapping set of a graph to determine the frequencies of its same order supergraphs simply in O(1) time without carrying out sub-graph isomorphism testing. The algorithm starts ingeniously with minimally connected query graphs of size k and finds their mappings in the network via sub-graph isomorphism. After that, with conservation of the graph size, it expands previously considered query graphs edge-by-edge and computes the frequency of these expanded graphs as mentioned above. The expansion process continues until reaching a complete graph Kk (fully connected with 模板:Frac edge).
As discussed above, the algorithm starts by computing sub-tree frequencies in the network and then expands sub-trees edge by edge. One way to implement this idea is called the expansion tree Tk for each k. Figure shows the expansion tree for size-4 sub-graphs. Tk organizes the running process and provides query graphs in a hierarchical manner. Strictly speaking, the expansion tree Tk is simply a directed acyclic graph or DAG, with its root number k indicating the graph size existing in the expansion tree and each of its other nodes containing the adjacency matrix of a distinct k-size query graph. Nodes in the first level of Tk are all distinct k-size trees and by traversing Tk in depth query graphs expand with one edge at each level. A query graph in a node is a sub-graph of the query graph in a node's child with one edge difference. The longest path in Tk consists of (k2-3k+4)/2 edges and is the path from the root to the leaf node holding the complete graph. Generating expansion trees can be done by a simple routine which is explained in.[41]
MODA traverses Tk and when it extracts query trees from the first level of Tk it computes their mapping sets and saves these mappings for the next step. For non-tree queries from Tk, the algorithm extracts the mappings associated with the parent node in Tk and determines which of these mappings can support the current query graphs. The process will continue until the algorithm gets the complete query graph. The query tree mappings are extracted using the Grochow–Kellis algorithm. For computing the frequency of non-tree query graphs, the algorithm employs a simple routine that takes O(1) steps. In addition, MODA exploits a sampling method where the sampling of each node in the network is linearly proportional to the node degree, the probability distribution is exactly similar to the well-known Barabási-Albert preferential attachment model in the field of complex networks.[42] This approach generates approximations; however, the results are almost stable in different executions since sub-graphs aggregate around highly connected nodes.[43] The pseudocode of MODA is shown below:
| MODA |
|---|
| Input: G: Input graph, k: sub-graph size, Δ: threshold value
Output: Frequent Subgraph List: List of all frequent k-size sub-graphs Note: FG: set of mappings from G in the input graph G fetch Tk do G′ = Get-Next-BFS(Tk) // G′ is a query graph if |E(G′)| = (k – 1) call Mapping-Module(G′, G) else call Enumerating-Module(G′, G, Tk) end if save F2 if |FG| > Δ then add G′ into Frequent Subgraph List end if Until |E(G')| = (k – 1)/2 return Frequent Subgraph List |
Kavosh
A recently introduced algorithm named Kavosh [44] aims at improved main memory usage. Kavosh is usable to detect NM in both directed and undirected networks. The main idea of the enumeration is similar to the GK and MODA algorithms, which first find all k-size sub-graphs that a particular node participated in, then remove the node, and subsequently repeat this process for the remaining nodes.[44]
For counting the sub-graphs of size k that include a particular node, trees with maximum depth of k, rooted at this node and based on neighborhood relationship are implicitly built. Children of each node include both incoming and outgoing adjacent nodes. To descend the tree, a child is chosen at each level with the restriction that a particular child can be included only if it has not been included at any upper level. After having descended to the lowest level possible, the tree is again ascended and the process is repeated with the stipulation that nodes visited in earlier paths of a descendant are now considered unvisited nodes. A final restriction in building trees is that all children in a particular tree must have numerical labels larger than the label of the root of the tree. The restrictions on the labels of the children are similar to the conditions which GK and ESU algorithm use to avoid overcounting sub-graphs.
The protocol for extracting sub-graphs makes use of the compositions of an integer. For the extraction of sub-graphs of size k, all possible compositions of the integer k-1 must be considered. The compositions of k-1 consist of all possible manners of expressing k-1 as a sum of positive integers. Summations in which the order of the summands differs are considered distinct. A composition can be expressed as k2,k3,…,km where k2 + k3 + … + km = k-1. To count sub-graphs based on the composition, ki nodes are selected from the i-th level of the tree to be nodes of the sub-graphs (i = 2,3,…,m). The k-1 selected nodes along with the node at the root define a sub-graph within the network. After discovering a sub-graph involved as a match in the target network, in order to be able to evaluate the size of each class according to the target network, Kavosh employs the nauty algorithm [33][34] in the same way as FANMOD. The enumeration part of Kavosh algorithm is shown below:
| Enumeration of Kavosh |
|---|
| Enumerate_Vertex(G, u, S, Remainder, i)
Input: G: Input graph if Remainder = 0 then |
| Validate(G, Parents, u) Input: G: input graph, Parents: selected vertices of last layer, u: Root vertex. ValList ← NILL |
Recently a Cytoscape plugin called CytoKavosh [45] is developed for this software. It is available via Cytoscape web page [1].
G-Tries
2010年, Pedro Ribeiro 和 Fernando Silva 提出了一个叫做g-trie的新数据结构,用来存储一组子图。[46]这个在概念上类似前缀树的数据结构,根据子图结构来进行存储,并找出了每个子图在一个更大的图中出现的次数。这个数据结构有一个突出的方面:在应用于模体发现算法时,主网络中的子图需要进行评估。因此,在随机网络中寻找那些在不在主网络中的子图,这个消耗时间的步骤就不再需要执行了。
g-trie 是一个存储一组图的多叉树。每一个树节点都存储着一个图节点及其对应的到前一个节点的边的信息。从根节点到叶节点的一条路径对应一个图。一个 g-trie 节点的子孙节点共享一个子图(即每一次路径的分叉意味着从一个子图结构中扩展出不同的图结构,而这些扩展出来的图结构自然有着相同的子图结构)。如何构造一个 g-trie 在[46]中有详细描述。构造好一个 g-trie 以后,需要进行计数步骤。计数流程的主要思想是回溯所有可能的子图,同时进行同构性测试。这种回溯技术本质上和其他以模体为中心的方法,比如MODA 和 GK 算法中使用的技术是一样的。这种技术利用了共同的子结构,亦即在一定时间内,几个不同的候选子图中存在部分是同构的。
在上述算法中,G-Tries 是最快的。然而,它的一个缺点是内存的超量使用,这局限了它在个人电脑运行时所能发现的模体的大小
对比
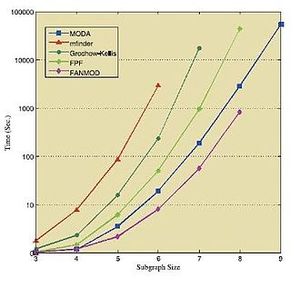
下面的表格和数据显示了在各种标准网络中运行上述算法所获得的结果。这些结果皆获取于各自相应的来源[41][44][46] ,因此需要独立地对待它们。
| 网络 | 子图大小 | 原始网络数据 | 随机网络平均数据 | ||||
|---|---|---|---|---|---|---|---|
| FANMOD | GK | G-Trie | FANMOD | GK | G-Trie | ||
| Dolphins | 5 | 0.07 | 0.03 | 0.01 | 0.13 | 0.04 | 0.01 |
| 6 | 0.48 | 0.28 | 0.04 | 1.14 | 0.35 | 0.07 | |
| 7 | 3.02 | 3.44 | 0.23 | 8.34 | 3.55 | 0.46 | |
| 8 | 19.44 | 73.16 | 1.69 | 67.94 | 37.31 | 4.03 | |
| 9 | 100.86 | 2984.22 | 6.98 | 493.98 | 366.79 | 24.84 | |
| Circuit | 6 | 0.49 | 0.41 | 0.03 | 0.55 | 0.24 | 0.03 |
| 7 | 3.28 | 3.73 | 0.22 | 3.53 | 1.34 | 0.17 | |
| 8 | 17.78 | 48.00 | 1.52 | 21.42 | 7.91 | 1.06 | |
| Social | 3 | 0.31 | 0.11 | 0.02 | 0.35 | 0.11 | 0.02 |
| 4 | 7.78 | 1.37 | 0.56 | 13.27 | 1.86 | 0.57 | |
| 5 | 208.30 | 31.85 | 14.88 | 531.65 | 62.66 | 22.11 | |
| Yeast | 3 | 0.47 | 0.33 | 0.02 | 0.57 | 0.35 | 0.02 |
| 4 | 10.07 | 2.04 | 0.36 | 12.90 | 2.25 | 0.41 | |
| 5 | 268.51 | 34.10 | 12.73 | 400.13 | 47.16 | 14.98 | |
| Power | 3 | 0.51 | 1.46 | 0.00 | 0.91 | 1.37 | 0.01 |
| 4 | 1.38 | 4.34 | 0.02 | 3.01 | 4.40 | 0.03 | |
| 5 | 4.68 | 16.95 | 0.10 | 12.38 | 17.54 | 0.14 | |
| 6 | 20.36 | 95.58 | 0.55 | 67.65 | 92.74 | 0.88 | |
| 7 | 101.04 | 765.91 | 3.36 | 408.15 | 630.65 | 5.17 | |
| 子图大小→ | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|
| 网络↓ | 算法↓ | ||||||||
| E. coli | Kavosh | 0.30 | 1.84 | 14.91 | 141.98 | 1374.0 | 13173.7 | 121110.3 | 1120560.1 |
| FANMOD | 0.81 | 2.53 | 15.71 | 132.24 | 1205.9 | 9256.6 | - | - | |
| Mavisto | 13532 | - | - | - | - | - | - | - | |
| Mfinder | 31.0 | 297 | 23671 | - | - | - | - | - | |
| Electronic | Kavosh | 0.08 | 0.36 | 8.02 | 11.39 | 77.22 | 422.6 | 2823.7 | 18037.5 |
| FANMOD | 0.53 | 1.06 | 4.34 | 24.24 | 160 | 967.99 | - | - | |
| Mavisto | 210.0 | 1727 | - | - | - | - | - | - | |
| Mfinder | 7 | 14 | 109.8 | 2020.2 | - | - | - | - | |
| Social | Kavosh | 0.04 | 0.23 | 1.63 | 10.48 | 69.43 | 415.66 | 2594.19 | 14611.23 |
| FANMOD | 0.46 | 0.84 | 3.07 | 17.63 | 117.43 | 845.93 | - | - | |
| Mavisto | 393 | 1492 | - | - | - | - | - | - | |
| Mfinder | 12 | 49 | 798 | 181077 | - | - | - | - |
算法的分类
正如表格所示,模体发现算法可以分为两大类:基于精确计数的算法,以及使用统计采样以及估计的算法。因为后者并不计数所有子图在主网络中出现的次数,所以第二类算法会更快,却也可能产生带有偏向性的,甚至不现实的结果。
更深一层地,基于精确计数的算法可以分为以网络为中心的方法以及以子图为中心的方法。前者在给定网络中搜索给定大小的子图,而后者首先根据给定大小生成各种可能的非同构图,然后在网络中分别搜索这些生成的图。这两种方法都有各自的优缺点,这些在上文有讨论。
另一方面,基于估计的方法可能会利用如前面描述过的颜色编码手段,其它的手段则通常会在枚举过程中忽略一些子图(比如,像在 FANMOD 中做的那样),然后只在枚举出来的子图上做估计。
此外,表格还指出了一个算法能否应用于有向网络或无向网络,以及导出子图或非导出子图。更多信息请参考下方提供的网页和实验室地址及联系方式。
| 计数方式 | 基础 | 算法名称 | 有向 / 无向 | 导出/ 非导出 |
|---|---|---|---|---|
| 精确基数 | 以网络为中心 | mfinder | 皆可 | 导出 |
| ESU (FANMOD) | 皆可 | 导出 | ||
| Kavosh (used in CytoKavosh) | 皆可 | 导出 | ||
| G-Tries | 皆可 | 导出 | ||
| PGD | 无向 | 导出 | ||
| 以子图为中心 | FPF (Mavisto) | 皆可 | 导出 | |
| NeMoFinder | 无向 | 导出 | ||
| Grochow–Kellis | 皆可 | Both | ||
| MODA | 皆可 | 皆可 | ||
| 采样估计 | 颜色编码 | N. Alon et al.’s Algorithm | 无向 | 非导出 |
| 其他手段 | mfinder | 皆可 | 导出 | |
| ESU (FANMOD) | 皆可 | 导出 |
| 算法 | 实验室/研究组 | 学院 | 大学/研究所 | 地址 | 电子邮件 |
|---|---|---|---|---|---|
| mfinder | Uri Alon's Group | Department of Molecular Cell Biology | Weizmann Institute of Science | Rehovot, Israel, Wolfson, Rm. 607 | urialon at weizmann.ac.il |
| FPF (Mavisto) | ---- | ---- | Leibniz-Institut für Pflanzengenetik und Kulturpflanzenforschung (IPK) | Corrensstraße 3, D-06466 Stadt Seeland, OT Gatersleben, Deutschland | schreibe at ipk-gatersleben.de |
| ESU (FANMOD) | Lehrstuhl Theoretische Informatik I | Institut für Informatik | Friedrich-Schiller-Universität Jena | Ernst-Abbe-Platz 2,D-07743 Jena, Deutschland | sebastian.wernicke at gmail.com |
| NeMoFinder | ---- | School of Computing | National University of Singapore | Singapore 119077 | chenjin at comp.nus.edu.sg |
| Grochow–Kellis | CS Theory Group & Complex Systems Group | Computer Science | University of Colorado, Boulder | 1111 Engineering Dr. ECOT 717, 430 UCB Boulder, CO 80309-0430 USA | jgrochow at colorado.edu |
| N. Alon et al.’s Algorithm | Department of Pure Mathematics | School of Mathematical Sciences | Tel Aviv University | Tel Aviv 69978, Israel | nogaa at post.tau.ac.il |
| MODA | Laboratory of Systems Biology and Bioinformatics (LBB) | Institute of Biochemistry and Biophysics (IBB) | University of Tehran | Enghelab Square, Enghelab Ave, Tehran, Iran | amasoudin at ibb.ut.ac.ir |
| Kavosh (used in CytoKavosh) | Laboratory of Systems Biology and Bioinformatics (LBB) | Institute of Biochemistry and Biophysics (IBB) | University of Tehran | Enghelab Square, Enghelab Ave, Tehran, Iran | amasoudin at ibb.ut.ac.ir |
| G-Tries | Center for Research in Advanced Computing Systems | Computer Science | University of Porto | Rua Campo Alegre 1021/1055, Porto, Portugal | pribeiro at dcc.fc.up.pt |
| PGD | Network Learning and Discovery Lab | Department of Computer Science | Purdue University | Purdue University, 305 N University St, West Lafayette, IN 47907 | nkahmed@purdue.edu |
Well-established motifs and their functions
Much experimental work has been devoted to understanding network motifs in gene regulatory networks. These networks control which genes are expressed in the cell in response to biological signals. The network is defined such that genes are nodes, and directed edges represent the control of one gene by a transcription factor (regulatory protein that binds DNA) encoded by another gene. Thus, network motifs are patterns of genes regulating each other's transcription rate. When analyzing transcription networks, it is seen that the same network motifs appear again and again in diverse organisms from bacteria to human. The transcription network of E. coli and yeast, for example, is made of three main motif families, that make up almost the entire network. The leading hypothesis is that the network motif were independently selected by evolutionary processes in a converging manner,[47][48] since the creation or elimination of regulatory interactions is fast on evolutionary time scale, relative to the rate at which genes change,[47][48][49] Furthermore, experiments on the dynamics generated by network motifs in living cells indicate that they have characteristic dynamical functions. This suggests that the network motif serve as building blocks in gene regulatory networks that are beneficial to the organism.
The functions associated with common network motifs in transcription networks were explored and demonstrated by several research projects both theoretically and experimentally. Below are some of the most common network motifs and their associated function.
Negative auto-regulation (NAR)
One of simplest and most abundant network motifs in E. coli is negative auto-regulation in which a transcription factor (TF) represses its own transcription. This motif was shown to perform two important functions. The first function is response acceleration. NAR was shown to speed-up the response to signals both theoretically [50] and experimentally. This was first shown in a synthetic transcription network[51] and later on in the natural context in the SOS DNA repair system of E .coli.[52] The second function is increased stability of the auto-regulated gene product concentration against stochastic noise, thus reducing variations in protein levels between different cells.[53][54][55]
Positive auto-regulation (PAR)
Positive auto-regulation (PAR) occurs when a transcription factor enhances its own rate of production. Opposite to the NAR motif this motif slows the response time compared to simple regulation.[56] In the case of a strong PAR the motif may lead to a bimodal distribution of protein levels in cell populations.[57]
Feed-forward loops (FFL)
This motif is commonly found in many gene systems and organisms. The motif consists of three genes and three regulatory interactions. The target gene C is regulated by 2 TFs A and B and in addition TF B is also regulated by TF A . Since each of the regulatory interactions may either be positive or negative there are possibly eight types of FFL motifs.[58] Two of those eight types: the coherent type 1 FFL (C1-FFL) (where all interactions are positive) and the incoherent type 1 FFL (I1-FFL) (A activates C and also activates B which represses C) are found much more frequently in the transcription network of E. coli and yeast than the other six types.[58][59] In addition to the structure of the circuitry the way in which the signals from A and B are integrated by the C promoter should also be considered. In most of the cases the FFL is either an AND gate (A and B are required for C activation) or OR gate (either A or B are sufficient for C activation) but other input function are also possible.
Coherent type 1 FFL (C1-FFL)
The C1-FFL with an AND gate was shown to have a function of a ‘sign-sensitive delay’ element and a persistence detector both theoretically [58] and experimentally[60] with the arabinose system of E. coli. This means that this motif can provide pulse filtration in which short pulses of signal will not generate a response but persistent signals will generate a response after short delay. The shut off of the output when a persistent pulse is ended will be fast. The opposite behavior emerges in the case of a sum gate with fast response and delayed shut off as was demonstrated in the flagella system of E. coli.[61] De novo evolution of C1-FFLs in gene regulatory networks has been demonstrated computationally in response to selection to filter out an idealized short signal pulse, but for non-idealized noise, a dynamics-based system of feed-forward regulation with different topology was instead favored.[62]
Incoherent type 1 FFL (I1-FFL)
The I1-FFL is a pulse generator and response accelerator. The two signal pathways of the I1-FFL act in opposite directions where one pathway activates Z and the other represses it. When the repression is complete this leads to a pulse-like dynamics. It was also demonstrated experimentally that the I1-FFL can serve as response accelerator in a way which is similar to the NAR motif. The difference is that the I1-FFL can speed-up the response of any gene and not necessarily a transcription factor gene.[63] An additional function was assigned to the I1-FFL network motif: it was shown both theoretically and experimentally that the I1-FFL can generate non-monotonic input function in both a synthetic [64] and native systems.[65] Finally, expression units that incorporate incoherent feedforward control of the gene product provide adaptation to the amount of DNA template and can be superior to simple combinations of constitutive promoters.[66] Feedforward regulation displayed better adaptation than negative feedback, and circuits based on RNA interference were the most robust to variation in DNA template amounts.[66]
Multi-output FFLs
In some cases the same regulators X and Y regulate several Z genes of the same system. By adjusting the strength of the interactions this motif was shown to determine the temporal order of gene activation. This was demonstrated experimentally in the flagella system of E. coli.[67]
Single-input modules (SIM)
This motif occurs when a single regulator regulates a set of genes with no additional regulation. This is useful when the genes are cooperatively carrying out a specific function and therefore always need to be activated in a synchronized manner. By adjusting the strength of the interactions it can create temporal expression program of the genes it regulates.[68]
In the literature, Multiple-input modules (MIM) arose as a generalization of SIM. However, the precise definitions of SIM and MIM have been a source of inconsistency. There are attempts to provide orthogonal definitions for canonical motifs in biological networks and algorithms to enumerate them, especially SIM, MIM and Bi-Fan (2x2 MIM).[69]
Dense overlapping regulons (DOR)
This motif occurs in the case that several regulators combinatorially control a set of genes with diverse regulatory combinations. This motif was found in E. coli in various systems such as carbon utilization, anaerobic growth, stress response and others.[21][26] In order to better understand the function of this motif one has to obtain more information about the way the multiple inputs are integrated by the genes. Kaplan et al.[70] has mapped the input functions of the sugar utilization genes in E. coli, showing diverse shapes.
已知的模体及其功能
许多实验工作致力于理解基因调控网络中的网络模体。在响应生物信号的过程中,这些网络控制细胞中需要表达的基因。这样的网络以基因作为节点,有向边代表对某个基因的调控,基因调控通过其他基因编码的转录因子结合在DNA上的调控蛋白来实现。因此,网络模体是基因之间相互调控转录速率的模式。在分析转录调控网络的时候,人们发现某些相同的网络模体在不同的物种中不断地出现,从细菌到人类。例如,大肠杆菌和酵母的转录网络由三种主要的网络模体家族组成,它们可以构建几乎整个网络。主要的假设是在进化的过程中,网络模体是被以收敛的方式独立选择出来的。[47][48] 因为相对于基因改变的速率,转录相互作用产生和消失的时间尺度在进化上是很快的。[47][48][49] 此外,对活细胞中网络模体所产生的动力学行为的实验表明,它们具有典型的动力学功能。这表明,网络模体是基因调控网络中对生物体有益的基本单元。
一些研究从理论和实验两方面探讨和论证了转录网络中与共同网络模体相关的功能。下面是一些最常见的网络模体及其相关功能。
负自反馈调控(NAR)
负自反馈调控是大肠杆菌中最简单和最冗余的网络模体之一,其中一个转录因子抑制它自身的转录。这种网络模体有两个重要的功能,其中第一个是加速响应。人们发现在实验和理论上, [50]NAR都可以加快对信号的响应。这个功能首先在一个人工合成的转录网络中被发现,[51] 然后在大肠杆菌SOS DAN修复系统这个自然体系中也被发现。[52] 负自反馈网络的第二个功能是增强自调控基因的产物浓度的稳定性,从而抵抗随机的噪声,减少该蛋白含量在不同细胞中的差异。[53][54][55]
正自反馈调控(PAR)
正自反馈调控是指转录因子增强它自身转录速率的调控。和负自反馈调节相反,NAR模体相比于简单的调控能够延长反应时间。[56] 在强PAR的情况下,模体可能导致蛋白质水平在细胞群中呈现双峰分布。[57]
前馈回路 (FFL)
前馈回路普遍存在于许多基因系统和生物体中。这种模体包括三个基因以及三个相互作用。目标基因C被两个转录因子(TFs)A和B调控,并且TF B同时被TF A调控。由于每个调控相互作用可以是正的或者负的,所以总共可能有八种类型的FFL模体。[58] 其中的两种:一致前馈回路的类型一(C1-FFL)(所有相互作用都是正的)和非一致前馈回路的类型一(I1-FFL)(A激活C和B,B抑制C)在大肠杆菌和酵母中相比于其他六种更频繁的出现。[58][59] 除了网络的结构外,还应该考虑来自A和B的信号被C的启动子集成的方式。在大多数情况下,FFL要么是一个与门(激活C需要A和B),要么是或门(激活C需要A或B),但也可以是其他输入函数。
一致前馈回路类型一(C1-FFL)
具有与门的C1-FFL有“符号-敏感延迟”单元和持久性探测器的功能,这一点在大肠杆菌阿拉伯糖系系统的理论[58]和实验上[60] 都有发现。这意味着该模体可以提供脉冲过滤,短脉冲信号不会产生响应,而持久信号在短延迟后会产生响应。当持久脉冲结束时,输出的关闭将很快。与此相反的行为出现在具有快速响应和延迟关闭特性的加和门的情况下,这在大肠杆菌的鞭毛系统中得到了证明。[61]在基因调控网络的重头进化中,对于滤除理想化的短信号脉冲作为进化压,C1-FFLs已经在计算上被证明可以进化出来。但是对于非理想化的噪声,不同拓扑结构前馈调节的动态系统将被优先考虑。 [71]
非一致前馈回路类型一(I1-FFL)
I1-FFL是一个脉冲生成器和响应加速器。I1-FFL的两种信号通路作用方向相反,一种通路激活Z,而另一种抑制Z。完全的抑制会导致类似脉冲的动力学行为。另外有实验证明,它可以类似于NAR模体起到响应加速器的作用。与NAR模体的不同之处在于,它可以加速任何基因的响应,而不必是转录因子。[63]I1-FFL网络还有另外一个功能:在理论和实验上都有证明I1-FFL可以生成非单调的输入函数,无论在人工合成的[64]还是自然的系统中。 [65] 最后,包含非一致前馈调控的基因生成物的表达单元对DNA模板的数量具有适应性,可以优于简单的组合本构启动子。[66] 前馈调控比负反馈具有更好的适应性,并且基于RNA干扰的网络对DNA模板数具有最高的鲁棒性。[66]
多输出前馈回路
在某些情况,相同的调控子X和Y可以调控同一系统中的多个Z基因。通过调节相互作用的强度,这些网络可以决定基因激活的时间顺序。这一点在大肠杆菌的鞭毛系统中有实验证据。[67]
单一输入模块(SIM)
当单个调控子调控一组基因,并且没有其他的调控因素时,这样的模体叫做单一输入模块(SIM)。当很多基因合作执行某个功能时这是有用的,因为这些基因需要同步地被激活。通过调节相互作用的强度,可以编排它所调控的基因表达的时间顺序。[68]
在文献中,多输入模块(MIM)来自于SIM的扩展。但是二者的精确定义并不太一致。有一些尝试给出生物网络中规范模体的正交定义,也有一些算法去枚举它们,特别是SIM,MIM和2x2 MIM等。[72]
密集交盖调节网(DOR)
这种类型的网络存在于多个调节子结合起来控制一组基因的情形,并且有多种调控的组合。这种模体出现在大肠杆菌的多种系统中,例如碳利用、厌氧生长、应激反应等。[21][26] 为了更好地理解这种网络,我们必须得到关于基因集成多种输入的方式的信息。Kaplan et al.[70]绘制了大肠杆菌糖利用基因的输入函数,表现出各种各样的形状。
活动模体/Activity motifs
An interesting generalization of the network-motifs, activity motifs are over occurring patterns that can be found when nodes and edges in the network are annotated with quantitative features. For instance, when edges in a metabolic pathways are annotated with the magnitude or timing of the corresponding gene expression, some patterns are over occurring given the underlying network structure.[73]
关于网络模体有一个有趣的概括: 在一个对节点(node)和边(edge)以量化标注的网络中,活动模体是反复的斑图。例如,当新城代谢的边以相应基因的表达量或时间来标注时,一些斑图在给定的底层网络结构里是反复的。[73]
批判 Criticism
An assumption (sometimes more sometimes less implicit) behind the preservation of a topological sub-structure is that it is of a particular functional importance. This assumption has recently been questioned. Some authors have argued that motifs, like bi-fan motifs, might show a variety depending on the network context, and therefore,[74] structure of the motif does not necessarily determine function. Network structure certainly does not always indicate function; this is an idea that has been around for some time, for an example see the Sin operon.[75]
关于拓扑子结构的一个(某种程度上隐含的)前提性假设是其具有特定的功能重要性。但这个假设最近遭到质疑,有人提出在不同的网络环境下模体可能表现出多样性,例如双扇模体,所以[74]模体的结构不必然决定功能,网络结构也不当然能揭示其功能;这种见解由来已久,可参见Sin 操纵子。[76]
Most analyses of motif function are carried out looking at the motif operating in isolation. Recent research[77] provides good evidence that network context, i.e. the connections of the motif to the rest of the network, is too important to draw inferences on function from local structure only — the cited paper also reviews the criticisms and alternative explanations for the observed data. An analysis of the impact of a single motif module on the global dynamics of a network is studied in.[78] Yet another recent work suggests that certain topological features of biological networks naturally give rise to the common appearance of canonical motifs, thereby questioning whether frequencies of occurrences are reasonable evidence that the structures of motifs are selected for their functional contribution to the operation of networks.[79][80]
大多数模体功能分析是基于模体孤立运行的情形。最近的研究[81]表明网络环境至关重要,不能忽视网络环境而仅从本地结构来对其功能进行推论——引用的论文还回顾了对观测数据的批判及其他可能的解释。人们研究了单个模体模组对网络全局的动力学影响及其分析[82]。而另一项近期的研究工作提出生物网络的某些拓扑特征自然地引起经典模体的常见形态,让人不禁疑问:发生频率是否能证明模体的结构是出于其对所在网络运行的功能性贡献而被保留下的结果?[83][84]
While the study of motifs was mostly applied to static complex networks, research of temporal complex networks[85] suggested a significant reinterpretation of network motifs, and introduced the concept of temporal network motifs. Braha and Bar-Yam[86] studied the dynamics of local motif structure in time-dependent/temporal networks, and find recurrent patterns that might provide empirical evidence for cycles of social interaction. Counter to the perspective of stable motifs and motif profiles in complex networks, they demonstrated that for temporal networks the local structure is time-dependent and might evolve over time. Braha and Bar-Yam further suggested that analyzing the temporal local structure might provide important information about the dynamics of system-level task and functionality.
模体的研究主要应用于静态复杂网络,而时变复杂网络的研究[87]对网络模体的提出了重大的新解释,并介绍了时变网络模体的概念。Braha和Bar-Yam[88]研究了
本地模体结构在时间依赖网络/时变网络的动力学,发现的一些反复模式有望成为社会互动周期的经验论据。他们证明了对于时变网络,其本地结构是时间依赖的且可能随时间演变,作为对复杂网络中稳定模体观及的模体表达观的反论,Braha和Bar-Yam进一步提出,时变本地结构的分析可能提供关于系统级任务和功能的动力信息重要信息。
See also
References
- ↑ 1.0 1.1 Masoudi-Nejad A, Schreiber F, Razaghi MK Z (2012). "Building Blocks of Biological Networks: A Review on Major Network Motif Discovery Algorithms". IET Systems Biology. 6 (5): 164–74. doi:10.1049/iet-syb.2011.0011. PMID 23101871.
- ↑ 2.0 2.1 Diestel R (2005). "Graph Theory (Graduate Texts in Mathematics)". 173. New York: Springer-Verlag Heidelberg.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ 3.0 3.1 3.2 3.3 Milo R, Shen-Orr SS, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (2002). "Network motifs: simple building blocks of complex networks". Science. 298 (5594): 824–827. Bibcode:2002Sci...298..824M. CiteSeerX 10.1.1.225.8750. doi:10.1126/science.298.5594.824. PMID 12399590.
- ↑ 4.0 4.1 Albert R, Barabási AL (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–49. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. CiteSeerX 10.1.1.242.4753. doi:10.1103/RevModPhys.74.47.
- ↑ 5.0 5.1 5.2 5.3 Milo R, Itzkovitz S, Kashtan N, Levitt R, Shen-Orr S, Ayzenshtat I, Sheffer M, Alon U (2004). "Superfamilies of designed and evolved networks". Science. 303 (5663): 1538–1542. Bibcode:2004Sci...303.1538M. doi:10.1126/science.1089167. PMID 15001784.
- ↑ 6.0 6.1 6.2 6.3 Schwöbbermeyer, H (2008). "Network Motifs". In Junker BH, Schreiber F (ed.). Analysis of Biological Networks. Hoboken, New Jersey: John Wiley & Sons. pp. 85–108.
- ↑ 7.0 7.1 Bornholdt, S; Schuster, HG (2003). "Handbook of graphs and networks : from the genome to the Internet". Handbook of Graphs and Networks: From the Genome to the Internet. p. 417. Bibcode:2003hgnf.book.....B.
- ↑ 8.0 8.1 8.2 8.3 Ciriello G, Guerra C (2008). "A review on models and algorithms for motif discovery in protein-protein interaction networks". Briefings in Functional Genomics and Proteomics. 7 (2): 147–156. doi:10.1093/bfgp/eln015. PMID 18443014.
- ↑ 9.0 9.1 9.2 9.3 9.4 9.5 Kashtan N, Itzkovitz S, Milo R, Alon U (2004). "Efficient sampling algorithm for estimating sub-graph concentrations and detecting network motifs". Bioinformatics. 20 (11): 1746–1758. doi:10.1093/bioinformatics/bth163. PMID 15001476.
- ↑ 10.0 10.1 10.2 10.3 10.4 10.5 Wernicke S (2006). "Efficient detection of network motifs". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 3 (4): 347–359. CiteSeerX 10.1.1.304.2576. doi:10.1109/tcbb.2006.51. PMID 17085844.
- ↑ 11.0 11.1 Picard F, Daudin JJ, Schbath S, Robin S (2005). "Assessing the Exceptionality of Network Motifs". J. Comp. Bio. 15 (1): 1–20. CiteSeerX 10.1.1.475.4300. doi:10.1089/cmb.2007.0137. PMID 18257674.
- ↑ 12.0 12.1 12.2 12.3 Frequency concepts and pattern detection for the analysis of motifs in networks. Lecture Notes in Computer Science. 3737. 2005. pp. 89–104. doi:10.1007/11599128_7. ISBN 978-3-540-30883-6.
- ↑ Holland, P. W., & Leinhardt, S. (1974). The statistical analysis of local structure in social networks. Working Paper No. 44, National Bureau of Economic Research.
- ↑ Hollandi, P., & Leinhardt, S. (1975). The Statistical Analysis of Local. Structure in Social Networks. Sociological Methodology, David Heise, ed. San Francisco: Josey-Bass.
- ↑ Holland, P. W., & Leinhardt, S. (1976). Local structure in social networks. Sociological methodology, 7, 1-45.
- ↑ Holland, P. W., & Leinhardt, S. (1977). A method for detecting structure in sociometric data. In Social Networks (pp. 411-432). Academic Press.
- ↑ Holland, P. W., & Leinhardt, S. (1974). The statistical analysis of local structure in social networks. Working Paper No. 44, National Bureau of Economic Research.
- ↑ Hollandi, P., & Leinhardt, S. (1975). The Statistical Analysis of Local. Structure in Social Networks. Sociological Methodology, David Heise, ed. San Francisco: Josey-Bass.
- ↑ Holland, P. W., & Leinhardt, S. (1976). Local structure in social networks. Sociological methodology, 7, 1-45.
- ↑ Holland, P. W., & Leinhardt, S. (1977). A method for detecting structure in sociometric data. In Social Networks (pp. 411-432). Academic Press.
- ↑ 21.0 21.1 21.2 21.3 21.4 Shen-Orr SS, Milo R, Mangan S, Alon U (May 2002). "Network motifs in the transcriptional regulation network of Escherichia coli". Nat. Genet. 31 (1): 64–8. doi:10.1038/ng881. PMID 11967538.
- ↑ 22.0 22.1 Eichenberger P, Fujita M, Jensen ST, et al. (October 2004). "The program of gene transcription for a single differentiating cell type during sporulation in Bacillus subtilis". PLOS Biology. 2 (10): e328. doi:10.1371/journal.pbio.0020328. PMC 517825. PMID 15383836.

- ↑ 23.0 23.1 Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (October 2002). "Network motifs: simple building blocks of complex networks". Science. 298 (5594): 824–7. Bibcode:2002Sci...298..824M. CiteSeerX 10.1.1.225.8750. doi:10.1126/science.298.5594.824. PMID 12399590.
- ↑ 24.0 24.1 Lee TI, Rinaldi NJ, Robert F, et al. (October 2002). "Transcriptional regulatory networks in Saccharomyces cerevisiae". Science. 298 (5594): 799–804. Bibcode:2002Sci...298..799L. doi:10.1126/science.1075090. PMID 12399584.
- ↑ 25.0 25.1 Odom DT, Zizlsperger N, Gordon DB, et al. (February 2004). "Control of pancreas and liver gene expression by HNF transcription factors". Science. 303 (5662): 1378–81. Bibcode:2004Sci...303.1378O. doi:10.1126/science.1089769. PMC 3012624. PMID 14988562.
- ↑ 26.0 26.1 26.2 26.3 Boyer LA, Lee TI, Cole MF, et al. (September 2005). "Core transcriptional regulatory circuitry in human embryonic stem cells". Cell. 122 (6): 947–56. doi:10.1016/j.cell.2005.08.020. PMC 3006442. PMID 16153702.
- ↑ 27.0 27.1 Iranfar N, Fuller D, Loomis WF (February 2006). "Transcriptional regulation of post-aggregation genes in Dictyostelium by a feed-forward loop involving GBF and LagC". Dev. Biol. 290 (2): 460–9. doi:10.1016/j.ydbio.2005.11.035. PMID 16386729.
- ↑ 28.0 28.1 Ma'ayan A, Jenkins SL, Neves S, et al. (August 2005). "Formation of regulatory patterns during signal propagation in a Mammalian cellular network". Science. 309 (5737): 1078–83. Bibcode:2005Sci...309.1078M. doi:10.1126/science.1108876. PMC 3032439. PMID 16099987.
- ↑ 29.0 29.1 Ptacek J, Devgan G, Michaud G, et al. (December 2005). "Global analysis of protein phosphorylation in yeast" (PDF). Nature (Submitted manuscript). 438 (7068): 679–84. Bibcode:2005Natur.438..679P. doi:10.1038/nature04187. PMID 16319894.
- ↑ "Acc-Motif: Accelerated Motif Detection".
- ↑ "Acc-Motif: Accelerated Motif Detection".
- ↑ Schreiber F, Schwobbermeyer H (2005). "MAVisto: a tool for the exploration of network motifs". Bioinformatics. 21 (17): 3572–3574. doi:10.1093/bioinformatics/bti556. PMID 16020473.
- ↑ 33.0 33.1 33.2 McKay BD (1981). "Practical graph isomorphism". Congressus Numerantium. 30: 45–87. arXiv:1301.1493. Bibcode:2013arXiv1301.1493M.
- ↑ 34.0 34.1 34.2 McKay BD (1998). "Isomorph-free exhaustive generation". Journal of Algorithms. 26 (2): 306–324. doi:10.1006/jagm.1997.0898.
- ↑ 35.0 35.1 Chen J, Hsu W, Li Lee M, et al. (2006). NeMoFinder: dissecting genome-wide protein-protein interactions with meso-scale network motifs. the 12th ACM SIGKDD international conference on Knowledge discovery and data mining. Philadelphia, Pennsylvania, USA. pp. 106–115.
- ↑ Huan J, Wang W, Prins J, et al. (2004). SPIN: mining maximal frequent sub-graphs from graph databases. the 10th ACM SIGKDD international conference on Knowledge discovery and data mining. pp. 581–586.
- ↑ Uetz P, Giot L, Cagney G, et al. (2000). "A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae". Nature. 403 (6770): 623–627. Bibcode:2000Natur.403..623U. doi:10.1038/35001009. PMID 10688190.
- ↑ 38.0 38.1 38.2 38.3 Grochow JA, Kellis M (2007). Network Motif Discovery Using Sub-graph Enumeration and Symmetry-Breaking (PDF). RECOMB. pp. 92–106. doi:10.1007/978-3-540-71681-5_7.
- ↑ 39.0 39.1 Grochow JA (2006). On the structure and evolution of protein interaction networks (PDF). Thesis M. Eng., Massachusetts Institute of Technology, Dept. of Electrical Engineering and Computer Science.
- ↑ 40.0 40.1 40.2 Alon N; Dao P; Hajirasouliha I; Hormozdiari F; Sahinalp S.C (2008). "Biomolecular network motif counting and discovery by color coding". Bioinformatics. 24 (13): i241–i249. doi:10.1093/bioinformatics/btn163. PMC 2718641. PMID 18586721.
- ↑ 41.0 41.1 41.2 41.3 41.4 Omidi S, Schreiber F, Masoudi-Nejad A (2009). "MODA: an efficient algorithm for network motif discovery in biological networks". Genes Genet Syst. 84 (5): 385–395. doi:10.1266/ggs.84.385. PMID 20154426.
- ↑ Barabasi AL, Albert R (1999). "Emergence of scaling in random networks". Science. 286 (5439): 509–512. arXiv:cond-mat/9910332. Bibcode:1999Sci...286..509B. doi:10.1126/science.286.5439.509. PMID 10521342.
- ↑ Vázquez A, Dobrin R, Sergi D, et al. (2004). "The topological relationship between the large-scale attributes and local interaction patterns of complex networks". PNAS. 101 (52): 17940–17945. arXiv:cond-mat/0408431. Bibcode:2004PNAS..10117940V. doi:10.1073/pnas.0406024101. PMC 539752. PMID 15598746.
- ↑ 44.0 44.1 44.2 44.3 Kashani ZR, Ahrabian H, Elahi E, Nowzari-Dalini A, Ansari ES, Asadi S, Mohammadi S, Schreiber F, Masoudi-Nejad A (2009). "Kavosh: a new algorithm for finding network motifs". BMC Bioinformatics. 10 (318): 318. doi:10.1186/1471-2105-10-318. PMC 2765973. PMID 19799800.

- ↑ Ali Masoudi-Nejad; Mitra Anasariola; Ali Salehzadeh-Yazdi; Sahand Khakabimamaghani (2012). "CytoKavosh: a Cytoscape Plug-in for Finding Network Motifs in Large Biological Networks". PLoS ONE. 7 (8): e43287. Bibcode:2012PLoSO...743287M. doi:10.1371/journal.pone.0043287. PMC 3430699. PMID 22952659.

- ↑ 46.0 46.1 46.2 46.3 Ribeiro P, Silva F (2010). G-Tries: an efficient data structure for discovering network motifs. ACM 25th Symposium On Applied Computing - Bioinformatics Track. Sierre, Switzerland. pp. 1559–1566.
- ↑ 47.0 47.1 47.2 47.3 Babu MM, Luscombe NM, Aravind L, Gerstein M, Teichmann SA (June 2004). "Structure and evolution of transcriptional regulatory networks". Current Opinion in Structural Biology. 14 (3): 283–91. CiteSeerX 10.1.1.471.9692. doi:10.1016/j.sbi.2004.05.004. PMID 15193307.
- ↑ 48.0 48.1 48.2 48.3 Conant GC, Wagner A (July 2003). "Convergent evolution of gene circuits". Nat. Genet. 34 (3): 264–6. doi:10.1038/ng1181. PMID 12819781.
- ↑ 49.0 49.1 Dekel E, Alon U (July 2005). "Optimality and evolutionary tuning of the expression level of a protein". Nature. 436 (7050): 588–92. Bibcode:2005Natur.436..588D. doi:10.1038/nature03842. PMID 16049495.
- ↑ 50.0 50.1 Zabet NR (September 2011). "Negative feedback and physical limits of genes". Journal of Theoretical Biology. 284 (1): 82–91. arXiv:1408.1869. CiteSeerX 10.1.1.759.5418. doi:10.1016/j.jtbi.2011.06.021. PMID 21723295.
- ↑ 51.0 51.1 Rosenfeld N, Elowitz MB, Alon U (November 2002). "Negative autoregulation speeds the response times of transcription networks". J. Mol. Biol. 323 (5): 785–93. CiteSeerX 10.1.1.126.2604. doi:10.1016/S0022-2836(02)00994-4. PMID 12417193.
- ↑ 52.0 52.1 Camas FM, Blázquez J, Poyatos JF (August 2006). "Autogenous and nonautogenous control of response in a genetic network". Proc. Natl. Acad. Sci. U.S.A. 103 (34): 12718–23. Bibcode:2006PNAS..10312718C. doi:10.1073/pnas.0602119103. PMC 1568915. PMID 16908855.
- ↑ 53.0 53.1 Becskei A, Serrano L (June 2000). "Engineering stability in gene networks by autoregulation". Nature. 405 (6786): 590–3. doi:10.1038/35014651. PMID 10850721.
- ↑ 54.0 54.1 Dublanche Y, Michalodimitrakis K, Kümmerer N, Foglierini M, Serrano L (2006). "Noise in transcription negative feedback loops: simulation and experimental analysis". Mol. Syst. Biol. 2 (1): 41. doi:10.1038/msb4100081. PMC 1681513. PMID 16883354.
- ↑ 55.0 55.1 Shimoga V, White J, Li Y, Sontag E, Bleris L (2013). "Synthetic mammalian transgene negative autoregulation". Mol. Syst. Biol. 9: 670. doi:10.1038/msb.2013.27. PMC 3964311. PMID 23736683.
- ↑ 56.0 56.1 Maeda YT, Sano M (June 2006). "Regulatory dynamics of synthetic gene networks with positive feedback". J. Mol. Biol. 359 (4): 1107–24. doi:10.1016/j.jmb.2006.03.064. PMID 16701695.
- ↑ 57.0 57.1 Becskei A, Séraphin B, Serrano L (May 2001). "Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion". EMBO J. 20 (10): 2528–35. doi:10.1093/emboj/20.10.2528. PMC 125456. PMID 11350942.
- ↑ 58.0 58.1 58.2 58.3 58.4 58.5 Mangan S, Alon U (October 2003). "Structure and function of the feed-forward loop network motif". Proc. Natl. Acad. Sci. U.S.A. 100 (21): 11980–5. Bibcode:2003PNAS..10011980M. doi:10.1073/pnas.2133841100. PMC 218699. PMID 14530388.
- ↑ 59.0 59.1 Ma HW, Kumar B, Ditges U, Gunzer F, Buer J, Zeng AP (2004). "An extended transcriptional regulatory network of Escherichia coli and analysis of its hierarchical structure and network motifs". Nucleic Acids Res. 32 (22): 6643–9. doi:10.1093/nar/gkh1009. PMC 545451. PMID 15604458.
- ↑ 60.0 60.1 Mangan S, Zaslaver A, Alon U (November 2003). "The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks". J. Mol. Biol. 334 (2): 197–204. CiteSeerX 10.1.1.110.4629. doi:10.1016/j.jmb.2003.09.049. PMID 14607112.
- ↑ 61.0 61.1 Kalir S, Mangan S, Alon U (2005). "A coherent feed-forward loop with a SUM input function prolongs flagella expression in Escherichia coli". Mol. Syst. Biol. 1 (1): E1–E6. doi:10.1038/msb4100010. PMC 1681456. PMID 16729041.
- ↑ Xiong, Kun; Lancaster, Alex K.; Siegal, Mark L.; Masel, Joanna (3 June 2019). "Feed-forward regulation adaptively evolves via dynamics rather than topology when there is intrinsic noise". Nature Communications. 10 (1): 2418. doi:10.1038/s41467-019-10388-6. PMC 6546794. PMID 31160574.
- ↑ 63.0 63.1 Mangan S, Itzkovitz S, Zaslaver A, Alon U (March 2006). "The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli". J. Mol. Biol. 356 (5): 1073–81. CiteSeerX 10.1.1.184.8360. doi:10.1016/j.jmb.2005.12.003. PMID 16406067.
- ↑ 64.0 64.1 Entus R, Aufderheide B, Sauro HM (August 2007). "Design and implementation of three incoherent feed-forward motif based biological concentration sensors". Syst Synth Biol. 1 (3): 119–28. doi:10.1007/s11693-007-9008-6. PMC 2398716. PMID 19003446.
- ↑ 65.0 65.1 Kaplan S, Bren A, Dekel E, Alon U (2008). "The incoherent feed-forward loop can generate non-monotonic input functions for genes". Mol. Syst. Biol. 4 (1): 203. doi:10.1038/msb.2008.43. PMC 2516365. PMID 18628744.
- ↑ 66.0 66.1 66.2 66.3 Bleris L, Xie Z, Glass D, Adadey A, Sontag E, Benenson Y (2011). "Synthetic incoherent feedforward circuits show adaptation to the amount of their genetic template". Mol. Syst. Biol. 7 (1): 519. doi:10.1038/msb.2011.49. PMC 3202791. PMID 21811230.
- ↑ 67.0 67.1 Kalir S, McClure J, Pabbaraju K, et al. (June 2001). "Ordering genes in a flagella pathway by analysis of expression kinetics from living bacteria". Science. 292 (5524): 2080–3. doi:10.1126/science.1058758. PMID 11408658.
- ↑ 68.0 68.1 Zaslaver A, Mayo AE, Rosenberg R, et al. (May 2004). "Just-in-time transcription program in metabolic pathways". Nat. Genet. 36 (5): 486–91. doi:10.1038/ng1348. PMID 15107854.
- ↑ Konagurthu AS, Lesk AM (2008). "Single and Multiple Input Modules in regulatory networks". Proteins. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061.
- ↑ 70.0 70.1 Kaplan S, Bren A, Zaslaver A, Dekel E, Alon U (March 2008). "Diverse two-dimensional input functions control bacterial sugar genes". Mol. Cell. 29 (6): 786–92. doi:10.1016/j.molcel.2008.01.021. PMC 2366073. PMID 18374652.
- ↑ Xiong, Kun; Lancaster, Alex K.; Siegal, Mark L.; Masel, Joanna (3 June 2019). "Feed-forward regulation adaptively evolves via dynamics rather than topology when there is intrinsic noise". Nature Communications. 10 (1): 2418. doi:10.1038/s41467-019-10388-6. PMC 6546794. PMID 31160574.
- ↑ Konagurthu AS, Lesk AM (2008). "Single and Multiple Input Modules in regulatory networks". Proteins. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061.
- ↑ 73.0 73.1 Chechik G, Oh E, Rando O, Weissman J, Regev A, Koller D (November 2008). "Activity motifs reveal principles of timing in transcriptional control of the yeast metabolic network". Nat. Biotechnol. 26 (11): 1251–9. doi:10.1038/nbt.1499. PMC 2651818. PMID 18953355.
- ↑ 74.0 74.1 Ingram PJ, Stumpf MP, Stark J (2006). "Network motifs: structure does not determine function". BMC Genomics. 7: 108. doi:10.1186/1471-2164-7-108. PMC 1488845. PMID 16677373.

- ↑ Voigt CA, Wolf DM, Arkin AP (March 2005). "The Bacillus subtilis sin operon: an evolvable network motif". Genetics. 169 (3): 1187–202. doi:10.1534/genetics.104.031955. PMC 1449569. PMID 15466432.
- ↑ Voigt CA, Wolf DM, Arkin AP (March 2005). "The Bacillus subtilis sin operon: an evolvable network motif". Genetics. 169 (3): 1187–202. doi:10.1534/genetics.104.031955. PMC 1449569. PMID 15466432.
- ↑ Knabe JF, Nehaniv CL, Schilstra MJ (2008). "Do motifs reflect evolved function?—No convergent evolution of genetic regulatory network subgraph topologies". BioSystems. 94 (1–2): 68–74. doi:10.1016/j.biosystems.2008.05.012. PMID 18611431.
- ↑ Taylor D, Restrepo JG (2011). "Network connectivity during mergers and growth: Optimizing the addition of a module". Physical Review E. 83 (6): 66112. arXiv:1102.4876. Bibcode:2011PhRvE..83f6112T. doi:10.1103/PhysRevE.83.066112. PMID 21797446.
- ↑ Konagurthu, Arun S.; Lesk, Arthur M. (23 April 2008). "Single and multiple input modules in regulatory networks". Proteins: Structure, Function, and Bioinformatics. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061.
- ↑ Konagurthu AS, Lesk AM (2008). "On the origin of distribution patterns of motifs in biological networks". BMC Syst Biol. 2: 73. doi:10.1186/1752-0509-2-73. PMC 2538512. PMID 18700017.

- ↑ Knabe JF, Nehaniv CL, Schilstra MJ (2008). "Do motifs reflect evolved function?—No convergent evolution of genetic regulatory network subgraph topologies". BioSystems. 94 (1–2): 68–74. doi:10.1016/j.biosystems.2008.05.012. PMID 18611431.
- ↑ Taylor D, Restrepo JG (2011). "Network connectivity during mergers and growth: Optimizing the addition of a module". Physical Review E. 83 (6): 66112. arXiv:1102.4876. Bibcode:2011PhRvE..83f6112T. doi:10.1103/PhysRevE.83.066112. PMID 21797446.
- ↑ Konagurthu, Arun S.; Lesk, Arthur M. (23 April 2008). "Single and multiple input modules in regulatory networks". Proteins: Structure, Function, and Bioinformatics. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061.
- ↑ Konagurthu AS, Lesk AM (2008). "On the origin of distribution patterns of motifs in biological networks". BMC Syst Biol. 2: 73. doi:10.1186/1752-0509-2-73. PMC 2538512. PMID 18700017.

- ↑ Braha, D., & Bar‐Yam, Y. (2006). From centrality to temporary fame: Dynamic centrality in complex networks. Complexity, 12(2), 59-63.
- ↑ Braha D., Bar-Yam Y. (2009) Time-Dependent Complex Networks: Dynamic Centrality, Dynamic Motifs, and Cycles of Social Interactions. In: Gross T., Sayama H. (eds) Adaptive Networks. Understanding Complex Systems. Springer, Berlin, Heidelberg
- ↑ Braha, D., & Bar‐Yam, Y. (2006). From centrality to temporary fame: Dynamic centrality in complex networks. Complexity, 12(2), 59-63.
- ↑ Braha D., Bar-Yam Y. (2009) Time-Dependent Complex Networks: Dynamic Centrality, Dynamic Motifs, and Cycles of Social Interactions. In: Gross T., Sayama H. (eds) Adaptive Networks. Understanding Complex Systems. Springer, Berlin, Heidelberg
