“网络模体”的版本间的差异

2020年5月11日 (一) 08:24的版本

所有网络，包括生物网络 biological networks、社交网络 social networks、技术网络（例如计算机网络和电路）等，都可以用图的形式来表示，这些图中会包括各种各样的子图 subgraphs。网络的一个重要的局部性质是所谓的网络模体，即重复且具有统计意义的子图或模式 patterns。

网络模体 Network motifs(NM)是指在特定网络或各种网络中重复出现的相同的子图。这些子图由顶点之间特定的交互模式定义，一个子图便可以反映一个框架，这个框架可以有效地实现某个特定的功能。事实上，之所以说模体是一个重要的特性，正是因为它们可能反映出对应网络功能的这一性质。近年来这一概念作为揭示复杂网络结构设计原理的一个有用概念而受到了广泛的关注。^[1] 但是，虽然通过研究网络模体可以深入了解网络的功能，但是对于模体的检测在计算上是具有挑战性的。

定义

设 $G = (V, E)$ 和 $G' = (V', E')$ 是两个图。若 $V' \subseteq V$ 且满足 $E' \subseteq E \cap (V' \times V')$ ）（即图 $G' \subseteq G$ 的所有边和点都属于图 $G$ ）则称图 $G' \subseteq G$ 是图 $G$ 的一个子图。若 $G' \subseteq G$ ，且对于顶点 $u$ 、 $v$ 及其连边，只要 $u$ 和 $v$ 存在于 $G'$ （即若 $U$ , $V' \subseteq V$ ），那么 $G' \subseteq G$ 中就应该包含原图 $G$ 中的所有 $u$ 和 $V$ 的对应连边（即 $〈u, v〉 \in E$ ），则称此时图 $G'$ 就是图 $G$ 的导出子图。如果存在一个双射（一对一） $f:V' \to V$ ，且对所有 $u, v \in V'$ 都有 $〈u, v〉 \in E' \Leftrightarrow 〈f(u), f(v)〉 \in E$ ，则称 $G'$ 是 $G$ 的同构图（记作： $G' \to G$ ），映射f则称为 $G$ 与 $G'$ 之间的同构 isomorphism。^[2]

当 $G″ \subset G$ ，且 $G″$ 与图 $G'$ 之间存在同构时，该映射表示 $G'$ 对于 $G$ 存在。图 $G'$ 在 $G$ 的出现次数称为 $G'$ 出现在 $G$ 的频率 $F G$ 。当一个子图的频率 $F G$ 高于预定的阈值或截止值时，则称 $G'$ 是 $G$ 中的递归（或频繁）子图。在接下来的内容中，我们交替使用术语“模式 motifs”和“频繁子图 frequent sub-graph”。

设从与 $G$ 相关联的零模型 the null-model获得的随机图集合为 $Ω(G)$ ，我们从 $Ω(G)$ 中均匀地选择N个随机图，并计算其特定频繁子图的频率。如果 $G'$ 出现在 $G$ 的频率高于N个随机图 $R i$ 的算术平均频率，其中 $1 \leq i \leq N$ ，我们称此递归模式是有意义的，因此可以将 $G'$ 视为 $G$ 的网络模体。对于一个小图 $G'$ ，网络 $G$ 和一组随机网络 $R(G) \subseteq Ω(R)$ ，当 $R(G) = N$ 时，由其Z分数 Z-score的定义如下式：

[math]\displaystyle{ Z(G^\prime) = \frac{F_G(G^\prime) - \mu_R(G^\prime)}{\sigma_R(G^\prime)} }[/math]

式中， $μ R (G')$ 和 $σ R (G')$ 分别代表集合 $R(G)$ 中的平均和标准偏差频率。^[3]^[4]^[5]^[6]^[7]^[8] $Z(G')$ 越大，子图 $G'$ 作为模体的意义也就越大。

此外还可以使用统计假设检验中的另一个测量方法，可以作为模体检测中的一种方法，即P值 P-value，以 $F R (G') \geq F G (G')$ 的概率给出（作为其零假设 null-hypothesis），其中 $F R (G')$ 表示随机网络中 $G'$ 的频率。^[6] 当P值小于阈值（通常为0.01或0.05）时，该子图可以被称为显著模式。该P值定义为：

[math]\displaystyle{ P(G^\prime) = \frac{1}{N}\sum_{i=1}^N \delta(c(i)) ; c(i): F_R^i(G^\prime) \ge F_G(G^\prime) }[/math]

图1 图中子图的不同出现. (M1 – M4) 是图（a）中子图（b）的不同出现。对于频率概念

F 1

,集合M1，M2，M3，M4表示所有匹配项，因此

F 1 = 4

。对于

F 2

，两个集合M1，M4或M2，M3之一是可能的匹配，

F 2 = 2

。最后，对于频率概念

F 3

仅允许匹配项之一（M1至M4），因此

F 3 = 1

。随着网元的使用受到限制，这三个频率概念的频率降低。

其中 $N$ 表示随机网络的数目， $i$ 定义在随机网络的集合上，若条件 $c(i)$ 成立，则Kroneckerδ函数 $δ(c(i))$ 是1。在网络 $G$ 中，一个特定的n维子图 $N'$ 的集中度^[9]^[10]是指子图在网络中出现频率与n维非同构子图的总频率之比，其计算公式如下：

[math]\displaystyle{ C_G(G^\prime) = \frac{F_G(G^\prime)}{\sum_i F_G(G_i)} }[/math]

其中索引 $i$ 定义在所有非同构 n 尺寸图的集合上。另一种统计测量是用来评估网络主题的，但在已知的算法中很少使用。这种测量方法是由 Picard 等人在2008年提出的，使用的是泊松分布，而不是上面隐含使用的高斯正态分布。^[11]

[math]\displaystyle{ C_G(G^\prime) = \frac{F_G(G^\prime)}{\sum_i F_G(G_i)} }[/math]

此外，他们还提出了子图频率的三个具体概念。^[12] 如图所示，第一频率概念 $F 1$ 考虑原始网络中图的所有匹配，这与我们前面介绍过的类似。第二个概念 $F 2$ 定义为原始网络中给定图的最大不相交边的数量。最后，频率概念 $F 3$ 包含与不相交边 disjoint edges和节点的匹配。因此，两个概念 $F 2$ 和 $F 3$ 限制了图元素的使用，并且可以看出，通过对网络元素的使用施加限制，子图的频率下降。因此，如果坚持使用频率概念 $F 2$ 和 $F 3$ ，网络模体检测算法将可以筛选出更多的候选子图。

历史

霍兰 Holland和莱因哈特 Leinhardt率先提出了网络三合会普查 a triad census of networks的概念，开创了网络模体研究的先河。^[13]^[14]^[15]^[16] 他们介绍了枚举各种子图配置的方法，并测试子图计数是否与随机网络中的期望值存在统计学上的差异。

2002年，Uri Alon和他的团队^[17]在大肠杆菌的基因调控 gene regulation network （转录 transcription）网络中发现了网络模体，随后在大量的自然网络中也发现了网络模体，从而进一步推广了这一观点。自那时起，许多科学家都对这一问题进行了大量的研究。其中一些研究集中在生物学应用上，而另一些则集中在网络模体的计算理论上。

生物学研究试图解释为生物网络检测到的模体。例如，在接下来的工作中，^[17]在大肠杆菌中发现的网络模体存在于其他细菌^[18]以及酵母^[19]^[20]和高等生物的转录网络中。^[21]^[22]^[23]在其他类型的生物网络中发现了一组不同的网络模体，如神经元网络和蛋白质相互作用网络。^[5]^[24]^[25]

另一方面，对于计算研究的重点则是改进现有的模体检测工具，以协助生物学研究，并允许对更大的网络进行分析。到目前为止，已经提供了几种不同的算法，这些算法将在下一节按时间顺序进行阐述。

最近，还发布了用于检测网络基序的acc基序工具。^[26]

模体发现算法

针对模体发现这一问题存在多种解决方案。这些算法可以归纳为不同的范式：例如精确计数方法，采样方法，模式增长方法等。但模体发现问题包括两个主要步骤：首先，计算子图的出现次数，然后评估子图的重要性。如果检测到的重现性远超过预期，那么这种重现性是很显著的。粗略地讲，子图的预期出现次数可以由零模型 Null-model 确定，该模型定义为具有与原始网络某些属性相同的随机网络的集合。

接下来，对下列算法的计算原理进行简要回顾，并从算法的角度讨论了它们的优缺点。

mfinder 算法

mfinder是第一个模体挖掘工具，它主要有两种模体查找算法：完全枚举 full enumeration 和采样方法 sampling method。直到2004年，用于NM检测的唯一精确计数方法是Milo等人提出的暴力穷举方法。^[3]该算法成功地发现了小规模的模体，但是这种方法甚至对于发现规模为5个或6个的模体在计算上都不可行的。因此，需要一种解决该问题的新方法。

Kashtan等人^[9]首次提出了一种基于边缘采样的网络模体采样发现算法。该算法估计了所含子图的集中度，可用于有向或无向网络中的模体发现。该算法的采样过程从网络的任意一条边开始，该边连向大小为2的子图，然后选择一条与当前子图相关的随机边对子图进行扩展。之后，它将继续选择随机的相邻边，直到获得大小为n的子图为止。最后，采样得到的子图扩展为包括这n个节点在内的网络中存在的所有边。当使用采样方法时，获取无偏样本是这类算法可能面临的最重要问题。而且，采样过程并不能保证采到所有的样本（也就是不能保证得到所有的子图），因此，Kashtan 等人又提出了一种加权方案，为网络中的不同子图分配不同的权重。^[9] 权重分配的基本原理是利用每个子图的抽样概率信息，即，与不可能的子图相比，可能的子图将获得相对较少的权重；因此，该算法必须计算已采样的每个子图的采样概率。这种加权技术有助于mfinder公正地确定子图的集中度。

与穷举搜索形成鲜明对比的是，该算法的计算时间竟然与网络大小渐近无关。对算法时间复杂度的分析表明，对于网络中大小为n的子图的每个样本，它的时间复杂度为[math]\displaystyle{ O(n^n) }[/math]。另一方面，并没有对已采样子图的每一个子图样本判断图同构问题的分类时间进行分析^[9]。另外，子图权重计算将额外增加该算法的计算负担。但是不得不指出的是，该算法可能会多次采样相同的子图——花费时间而不收集任何有用信息。^[10]总之，通过利用采样的优势，该算法的性能比穷举搜索算法更有效；但是，它只能大致确定子图的集中度。由于该算法的实现方式，使得它可以找到最大为6的模体，并且它会给出的最重要的模体，而不是其他所有模体。另外，有必要提到此工具没有可视化的呈现。采样算法简要显示如下：

mfinder
定义：[math]\displaystyle{ E_{s} }[/math]是采集的边集合。[math]\displaystyle{ V_{s} }[/math]是[math]\displaystyle{ E }[/math]中所有边的顶点的集合。
初始化[math]\displaystyle{ V_{s} }[/math]和[math]\displaystyle{ E_{s} }[/math]为空集。 1. 随机选择一条边[math]\displaystyle{ e_{1} = (v_{i}, v_{j}) }[/math]，更新 [math]\displaystyle{ E_{s} = \{e_{1}\}, V{s} = \{v_{i}, v_{j}\} }[/math] 2. 列出[math]\displaystyle{ E{s} }[/math]的所有邻边列表[math]\displaystyle{ L }[/math]，从[math]\displaystyle{ L }[/math]中删除[math]\displaystyle{ V{s} }[/math]中所有元素组成的边。 3. 从[math]\displaystyle{ L }[/math]中随机选择一条边[math]\displaystyle{ e = \{v_{k},v_{l}\} }[/math]，更新[math]\displaystyle{ E_{s} = E_{s} \cup \{e\} , V_{s} = V_{s} \cup \{v_{k}, v_{l}\} }[/math]。 4. 重复步骤2-3，直到完成包含n个节点的子图 ([math]\displaystyle{ \left \| V_{s} \right \| = n }[/math])。 5. 计算对选取的n节点子图进行采样的概率。

FPF (Mavisto)算法

Schreiber和Schwöbbermeyer ^[12]提出了一种称为灵活模式查找器（FPF）的算法，用于提取输入网络的频繁子图，并将其在名为Mavisto的系统中加以实现。^[27] 他们的算法利用了向下闭包特性，该特性适用于频率概念[math]\displaystyle{ F_{2} }[/math]和[math]\displaystyle{ F_{3} }[/math]。向下闭包性质表明，子图的频率随着子图的大小而单调下降；但这一性质并不一定适用于频率概念[math]\displaystyle{ F_{1} }[/math]。FPF算法基于模式树（见右图），由代表不同图形（或模式）的节点组成，其中每个节点的父节点是其子节点的子图；换句话说，每个模式树节点的对应图通过向其父节点图添加新边来扩展。

FPF算法中的模式树展示.^[12]

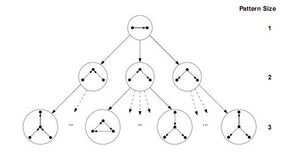
首先，FPF算法枚举并维护位于模式树根部的子图的所有匹配信息。然后，它通过在目标图中添加匹配边缘支持的一条边缘，在模式树中一一建立前一节点的子节点，然后通过在目标图中添加匹配边支持的一条边，逐个构建模式树中前一个节点的子节点，并尝试将以前关于匹配的所有信息拓展到新的子图(子节点)中。下一步，它判断当前模式的频率是否低于预定义的阈值。如果它低于阈值且保持向下闭包，则FPF算法会放弃该路径，而不会在树的此部分进一步遍历；这样就避免了不必要的计算。重复此过程，直到没有剩余可遍历的路径为止。

该算法的优点是它不会考虑不频繁的子图，并尝试尽快完成枚举过程；因此，它只花时间在模式树中用于有希望的节点上，而放弃所有其他节点。还有一点额外的好处，模式树概念允许 FPF 以并行方式实现和执行，因为它可以独立地遍历模式树的每个路径。但是，FPF对于频率概念[math]\displaystyle{ F_{2} }[/math]和[math]\displaystyle{ F_{3} }[/math]最为有用，因为向下闭包不适用于[math]\displaystyle{ F_{1} }[/math]。尽管如此，如果算法并行运行，那么模式树对于[math]\displaystyle{ F_{1} }[/math]仍然是可行的。该算法的另一个优点是它的实现对模体大小没有限制，这使其更易于改进。FPF（Mavisto）的伪代码如下所示：

Mavisto
数据: 图 [math]\displaystyle{ G }[/math], 目标模式规模 [math]\displaystyle{ t }[/math], 频率概念 [math]\displaystyle{ F }[/math]。结果: 以最大频率设置大小为 [math]\displaystyle{ t }[/math]的模式 [math]\displaystyle{ R }[/math].
[math]\displaystyle{ R \leftarrow \Phi , f_{max}\leftarrow 0 }[/math] [math]\displaystyle{ P \leftarrow }[/math] 开始于大小为1的模式 [math]\displaystyle{ p_{1} }[/math] [math]\displaystyle{ M_{p_{1}} \leftarrow }[/math] 图 [math]\displaystyle{ G }[/math] 中模式 [math]\displaystyle{ p_{1} }[/math] 的所有匹配当 [math]\displaystyle{ P \neq \Phi }[/math] 时，执行： [math]\displaystyle{ P_{max} \leftarrow }[/math] 从 [math]\displaystyle{ P }[/math] 中选择最大规模的所有模式 [math]\displaystyle{ P\leftarrow }[/math] 从 [math]\displaystyle{ P_{max} }[/math] 中选择最大频率的模式 [math]\displaystyle{ E = ExtensionLoop(G, p, M_{p}) }[/math] 对于 [math]\displaystyle{ p \in E }[/math] 的所有模式：如果 [math]\displaystyle{ F = F_{1} }[/math] ，那么 [math]\displaystyle{ f \leftarrow size(M_{p}) }[/math] 其他[math]\displaystyle{ f \leftarrow }[/math] 最大独立集 [math]\displaystyle{ (F, M_{p}) }[/math] 结束如果 [math]\displaystyle{ size(p) = t }[/math] ，那么如果 [math]\displaystyle{ f = f_{max} }[/math] ，那么 [math]\displaystyle{ R \leftarrow R \cup \{p\} }[/math] 其他如果 [math]\displaystyle{ f \gt f_{max} }[/math] ，那么 [math]\displaystyle{ R \leftarrow \{p\} }[/math]； [math]\displaystyle{ f_{max} \leftarrow f }[/math] 结束其他如果 [math]\displaystyle{ F = F_{1} or f \geq f_{max} }[/math] ，那么 [math]\displaystyle{ P \leftarrow P \cup \{p\} }[/math] 结束结束结束结束

ESU (FANMOD)算法及对应的软件

由于Kashtan等学者发现的采样偏差问题， ^[9]所以针对NM发现问题需要设计更好的算法。虽然Kashtan等人尝试用加权法来解决这个弊端，但这个方法在运行上，消耗了过多的运行时间，且实现起来也变得更加复杂。但这个工具还是最好用的工具之一，因为它支持可视化选项，同时也是个节约时间的算法。但是，它在所支持的模体的规模大小还是有局限性。由于该工具在具体实施中，不允许搜索规模大小为9或者更大的模体。

Weinicke^[10] 引入了一种叫RAND-ESU的算法，这个新引入的算法比Mfinder软件有着更显著的提升。.^[9] RAND-ESU基于精准的ESU算法，已有对应的软件FANMOD。^[10]RAND-ESU是一种NM发现算法，可应用于定向的或者不定向的网络中，能够有效的在网络中利用无偏差节点进行采样，以及保证了一个子图仅仅被搜索一次,且不会产生无意义的子图。并且，RAND-ESU采用了一个叫做DIRECT的全新的分析方式，从而来确定子图的重要性，而不是用随机网络的组合来建立Null模型。DIRECT方法可以不用大量生成随机网络就能估计子图的浓度。实际上，相较于用随机网络组合分析比较低集中度的子图来说，DIRECT这个方法更加的高效。但是，传统的Null模型比DIRECT这个算法能更加快速地解决高度集中的子图。接下来，我们将详细讲述ESU算法和展示如何把这种精确的算法调整为RAND-ESU算法去估计子图的集中度。

ESU和RAND-ESU两种算法都比较简捷，所以实现起来都很容易。ESU首先找到大小为 $k$ 的所有诱导子图的集合，并命名这个集合为 $S k$ 。因为EUS以递归函数的形式实现，该函数的运行可以演示为深度为 $k$ 的树状结构，称为ESU-Tree（见图）。每一个在ESU-Tree上的节点都表示递归函数的状态，这个递归函数需要两个连续集合的SUB和EXT。SUB指的是在目标网络的相邻节点上 $|SUB| \leq k$ 。如果 $|SUB| = k$ ，那么这个算法可以找到一个完整的诱导子图，所以在此情况下 $S k = SUB \cup S k$ 。相反，如果 $|SUB| < k$ ，那么这个算法必须把SUB扩大，才能实现基数为 $k$ 。EXT这个集合包含了所有的满足以下两个情况的节点。第一，每个在EXT的节点必须至少与在SUB的一个节点相邻。第二，他们的下标必须比在SUB的第一个元素大。第一个条件保证了SUB节点的展开产生相关的图，第二个条件能使ESU-Tree树状图上的分支变得离散。所以，这个方法可以避免过度计算。注意，EXT集合不是一个固定的集合。所以每一步都有可能扩展满足于以上两个条件的新节点。下一步包含了在ESU-Tree分支上的子图的分类，将它们分为非同构的大小为 $k$ 的图类。因此，ESU决定了子图的『频率以及浓度』。这一阶段的实施仅通过运用McKay的nauty算法，^[28]^[29]这一算法可以通过图的同构测试来把每个子图进行分类。所以，ESU能够在目标图中通过递归算法，找到所有规模大小为 $k$ 的诱导子图集合，且使用高效的工具来确定他们的频率。

运用RAND-ESU的过程十分的简单，这也是FANMOD的一个主要的优点。可以通过对ESU-Tree树状图的每个级别应用概率 $0 \leq p d \leq 1$ 并强制ESU以概率 $p d$ 遍历 $d-1$ 级别中节点的每个子节点，来更改ESU算法使其仅搜索ESU-Tree分支的一部分。这种新的演算方式叫RAND-ESU。显然，当所有阶段 $p d = 1$ 时，RAND-ESU等同于ESU。当 $p d = 0$ 时，在这个算法下没有任何意义。注意，这个过程只是确保了可以找到ESU-Tree上的每一分支的机会都是相同的，从而使网络中的子图采样无偏差。访问每个分支的概率为 $\prod d p d$ ，这对于所有ESU-Tree中的分支都是相同的；因此，该方法可确保从网络中对子图进行无偏采样。但是，设置 $1 \leq d \leq k$ 的 $p d$ 参数是另一个问题，必须由专家人工确定才能获得子图集中度的精确结果。^[8] 尽管对此没有明确的规定，但是Wrenucke提出了一些一般性的观察结论，这些结论有可能可以帮助我们确定p_d值。总的来说，在诱导子图支持无偏采样方法的情况下，RAND-ESU是一个能快速解决NM发现问题的算法。尽管，ESU算法的主要部分和FANMOD工具是以用来寻找诱导子图而著称的，但只需对ESU进行细小的改动，就可以用来寻找诱导子图。ESU（FANMOD）的伪代码如下：

图（a）大小为5的目标图，图（b）深度为k的ESU树，与目标图中大小为3的子图的提取相关。叶子对应于目标图（a）的集合S3或所有大小3诱导子图。ESU树中的节点包括两个相邻的集合，第一个集合包含称为SUB的相邻节点，第二个名为EXT的集合保存与至少一个SUB节点相邻且其数字标签大于SUB节点的所有节点标签。该算法利用EXT集扩展SUB集，直到达到所需的子图大小为止，该子图大小位于ESU-Tree（或其叶）的最低级别。

ESU子图搜索算法(FANMOD软件实现)
枚举子图(G,k) 输入: 图 $G = (V, E)$ 和一个整数 $1 \leq k \leq \|V\|$ . 输出: 所有size- $k$ 子图 in $G$ . for each顶点v $v \in V$ 执行 $VExtension（集合EXT） \leftarrow {u \in N({v}) \| u > v$ } 调用 $ExtendSubgraph ({v}, VExtension, v)$ 结束for循环
ExtendSubgraph(VSubgraph, VExtension, v) 若 $\|VSubgraph\| = k$ 则输出 $G[VSubgraph]$ and 返回主函数当 $VExtension \neq \emptyset$ 执行删除一个任意选择的顶点 $w$ 源于 $VExtension$ 中 $VExtension' \leftarrow VExtension \cup {u \in N excl (w, VSubgraph) \| u > v$ } call $ExtendSubgraph (VSubgraph \cup {w}, VExtension', v)$ 返回

G-Tries

2010年， Pedro Ribeiro 和 Fernando Silva 提出了一个叫做“g-trie”的新数据结构，用来存储一组子图。^[30]这个在概念上类似前缀树的数据结构，根据子图结构来进行存储，并找出了每个子图在一个更大的图中出现的次数。这个数据结构有一个突出的方面：在应用于模体发现算法时，主网络中的子图需要进行评估。因此，在随机网络中寻找那些在不在主网络中的子图，这个消耗时间的步骤就不再需要执行了。

g-trie是一个存储一组图的多叉树。每一个树节点都存储着一个图节点及其对应的到前一个节点的边的信息。从根节点到叶节点的一条路径对应一个图。一个g-trie节点的子孙节点共享一个子图（即每一次路径的分叉意味着从一个子图结构中扩展出不同的图结构，而这些扩展出来的图结构自然有着相同的子图结构）。如何构造一个g-trie在^[30]中有详细描述。构造好一个g-trie以后，需要进行计数步骤。计数流程的主要思想是回溯所有可能的子图，同时进行同构性测试。这种回溯技术本质上和其他以模体为中心的方法，比如 MODA 和 GK 算法中使用的技术是一样的。这种技术利用了共同的子结构，亦即在一定时间内，几个不同的候选子图中存在部分是同构的。

在上述算法中，G-Tries是最快的。然而，它的一个缺点是内存的超量使用，这局限了它在个人电脑运行时所能发现的模体的大小

对比

下面的表格和数据显示了在各种标准网络中运行上述算法所获得的结果。这些结果皆获取于各自相应的来源 ^[31] ^[32]^[30] ，因此需要独立地对待它们。

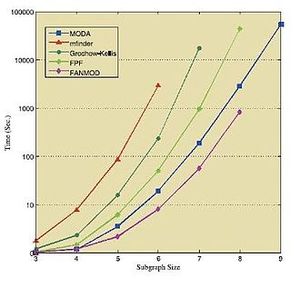
Grochow–Kellis，mfinder，FANMOD，FPF和MODA的运行时间适用于从三个节点到多达九个节点的子图。^[31]

Grochow–Kellis, FANMOD, 和 G-Trie 在5个不同网络上生成含3到9个节点子图所用的运行时间 ^[30]
网络	子图大小	原始网络数据			随机网络平均数据
网络	子图大小	FANMOD	GK	G-Trie	FANMOD	GK	G-Trie
Dolphins	5	0.07	0.03	0.01	0.13	0.04	0.01
	6	0.48	0.28	0.04	1.14	0.35	0.07
	7	3.02	3.44	0.23	8.34	3.55	0.46
	8	19.44	73.16	1.69	67.94	37.31	4.03
	9	100.86	2984.22	6.98	493.98	366.79	24.84
Circuit	6	0.49	0.41	0.03	0.55	0.24	0.03
	7	3.28	3.73	0.22	3.53	1.34	0.17
	8	17.78	48.00	1.52	21.42	7.91	1.06
Social	3	0.31	0.11	0.02	0.35	0.11	0.02
	4	7.78	1.37	0.56	13.27	1.86	0.57
	5	208.30	31.85	14.88	531.65	62.66	22.11
Yeast	3	0.47	0.33	0.02	0.57	0.35	0.02
	4	10.07	2.04	0.36	12.90	2.25	0.41
	5	268.51	34.10	12.73	400.13	47.16	14.98
Power	3	0.51	1.46	0.00	0.91	1.37	0.01
	4	1.38	4.34	0.02	3.01	4.40	0.03
	5	4.68	16.95	0.10	12.38	17.54	0.14
	6	20.36	95.58	0.55	67.65	92.74	0.88
	7	101.04	765.91	3.36	408.15	630.65	5.17

mfinder, FANMOD, Mavisto 和 Kavosh 在3个不同网络上生成含3到10个节点子图所用的运行时间^[32]
	子图大小→	3	4	5	6	7	8	9	10
网络↓	算法↓	3	4	5	6	7	8	9	10
E. coli	Kavosh	0.30	1.84	14.91	141.98	1374.0	13173.7	121110.3	1120560.1
	FANMOD	0.81	2.53	15.71	132.24	1205.9	9256.6	-	-
	Mavisto	13532	-	-	-	-	-	-	-
	Mfinder	31.0	297	23671	-	-	-	-	-
Electronic	Kavosh	0.08	0.36	8.02	11.39	77.22	422.6	2823.7	18037.5
	FANMOD	0.53	1.06	4.34	24.24	160	967.99	-	-
	Mavisto	210.0	1727	-	-	-	-	-	-
	Mfinder	7	14	109.8	2020.2	-	-	-	-
Social	Kavosh	0.04	0.23	1.63	10.48	69.43	415.66	2594.19	14611.23
	FANMOD	0.46	0.84	3.07	17.63	117.43	845.93	-	-
	Mavisto	393	1492	-	-	-	-	-	-
	Mfinder	12	49	798	181077	-	-	-	-

算法的分类

正如表格所示，模体发现算法可以分为两大类：基于精确计数的算法，以及使用统计采样以及估计的算法。因为后者并不计数所有子图在主网络中出现的次数，所以第二类算法会更快，却也可能产生带有偏向性的，甚至不现实的结果。

更深一层地，基于精确计数的算法可以分为以网络为中心的方法以及以子图为中心的方法。前者在给定网络中搜索给定大小的子图，而后者首先根据给定大小生成各种可能的非同构图，然后在网络中分别搜索这些生成的图。这两种方法都有各自的优缺点，这些在上文有讨论。

另一方面，基于估计的方法可能会利用如前面描述过的颜色编码手段，其它的手段则通常会在枚举过程中忽略一些子图(比如，像在 FANMOD 中做的那样)，然后只在枚举出来的子图上做估计。

此外，表格还指出了一个算法能否应用于有向网络或无向网络，以及导出子图或非导出子图。更多信息请参考下方提供的网页和实验室地址及联系方式。

模体发现算法的分类
计数方式	基础	算法名称	有向 / 无向	导出/ 非导出
精确基数	以网络为中心	mfinder	皆可	导出
		ESU (FANMOD)	皆可	导出
		Kavosh (used in CytoKavosh)	皆可	导出
		G-Tries	皆可	导出
		PGD	无向	导出
	以子图为中心	FPF (Mavisto)	皆可	导出
		NeMoFinder	无向	导出
		Grochow–Kellis	皆可	Both
		MODA	皆可	皆可
采样估计	颜色编码	N. Alon et al.’s Algorithm	无向	非导出
	其他手段	mfinder	皆可	导出
	其他手段	ESU (FANMOD)	皆可	导出

算法提出者的地址和联系方式
算法	实验室/研究组	学院	大学/研究所	地址	电子邮件
mfinder	Uri Alon's Group	Department of Molecular Cell Biology	Weizmann Institute of Science	Rehovot, Israel, Wolfson, Rm. 607	urialon at weizmann.ac.il
FPF (Mavisto)	----	----	Leibniz-Institut für Pflanzengenetik und Kulturpflanzenforschung (IPK)	Corrensstraße 3, D-06466 Stadt Seeland, OT Gatersleben, Deutschland	schreibe at ipk-gatersleben.de
ESU (FANMOD)	Lehrstuhl Theoretische Informatik I	Institut für Informatik	Friedrich-Schiller-Universität Jena	Ernst-Abbe-Platz 2,D-07743 Jena, Deutschland	sebastian.wernicke at gmail.com
NeMoFinder	----	School of Computing	National University of Singapore	Singapore 119077	chenjin at comp.nus.edu.sg
Grochow–Kellis	CS Theory Group & Complex Systems Group	Computer Science	University of Colorado, Boulder	1111 Engineering Dr. ECOT 717, 430 UCB Boulder, CO 80309-0430 USA	jgrochow at colorado.edu
N. Alon et al.’s Algorithm	Department of Pure Mathematics	School of Mathematical Sciences	Tel Aviv University	Tel Aviv 69978, Israel	nogaa at post.tau.ac.il
MODA	Laboratory of Systems Biology and Bioinformatics (LBB)	Institute of Biochemistry and Biophysics (IBB)	University of Tehran	Enghelab Square, Enghelab Ave, Tehran, Iran	amasoudin at ibb.ut.ac.ir
Kavosh (used in CytoKavosh)	Laboratory of Systems Biology and Bioinformatics (LBB)	Institute of Biochemistry and Biophysics (IBB)	University of Tehran	Enghelab Square, Enghelab Ave, Tehran, Iran	amasoudin at ibb.ut.ac.ir
G-Tries	Center for Research in Advanced Computing Systems	Computer Science	University of Porto	Rua Campo Alegre 1021/1055, Porto, Portugal	pribeiro at dcc.fc.up.pt
PGD	Network Learning and Discovery Lab	Department of Computer Science	Purdue University	Purdue University, 305 N University St, West Lafayette, IN 47907	nkahmed@purdue.edu

已知的模体及其功能

许多实验工作致力于理解基因调控网络中的网络模体。在响应生物信号的过程中，这些网络控制细胞中需要表达的基因。这样的网络以基因作为节点，有向边代表对某个基因的调控，基因调控通过其他基因编码的转录因子结合在DNA上的调控蛋白来实现。因此，网络模体是基因之间相互调控转录速率的模式。在分析转录调控网络的时候，人们发现某些相同的网络模体在不同的物种中不断地出现，从细菌到人类。例如，大肠杆菌和酵母的转录网络由三种主要的网络模体家族组成，它们可以构建几乎整个网络。主要的假设是在进化的过程中，网络模体是被以收敛的方式独立选择出来的。^[33]^[34] 因为相对于基因改变的速率，转录相互作用产生和消失的时间尺度在进化上是很快的。^[33]^[34]^[35] 此外，对活细胞中网络模体所产生的动力学行为的实验表明，它们具有典型的动力学功能。这表明，网络模体是基因调控网络中对生物体有益的基本单元。

一些研究从理论和实验两方面探讨和论证了转录网络中与共同网络模体相关的功能。下面是一些最常见的网络模体及其相关功能。

负自反馈调控(NAR)

自动调节基序的示意图

负自反馈调控是大肠杆菌中最简单和最冗余的网络模体之一，其中一个转录因子抑制它自身的转录。这种网络模体有两个重要的功能，其中第一个是加速响应。人们发现在实验和理论上， ^[36]NAR都可以加快对信号的响应。这个功能首先在一个人工合成的转录网络中被发现，^[37] 然后在大肠杆菌SOS DAN修复系统这个自然体系中也被发现。^[38] 负自反馈网络的第二个功能是增强自调控基因的产物浓度的稳定性，从而抵抗随机的噪声，减少该蛋白含量在不同细胞中的差异。^[39]^[40]^[41]

正自反馈调控(PAR)

正自反馈调控是指转录因子增强它自身转录速率的调控。和负自反馈调节相反，NAR模体相比于简单的调控能够延长反应时间。^[42] 在强PAR的情况下，模体可能导致蛋白质水平在细胞群中呈现双峰分布。^[43]

前馈回路 (FFL)

前馈主题的示意图

前馈回路普遍存在于许多基因系统和生物体中。这种模体包括三个基因以及三个相互作用。目标基因C被两个转录因子（TFs）A和B调控，并且TF B同时被TF A调控。由于每个调控相互作用可以是正的或者负的，所以总共可能有八种类型的FFL模体。^[44] 其中的两种：一致前馈回路的类型一（C1-FFL）（所有相互作用都是正的）和非一致前馈回路的类型一（I1-FFL）（A激活C和B，B抑制C）在大肠杆菌和酵母中相比于其他六种更频繁的出现。^[44]^[45] 除了网络的结构外，还应该考虑来自A和B的信号被C的启动子集成的方式。在大多数情况下，FFL要么是一个与门(激活C需要A和B)，要么是或门(激活C需要A或B)，但也可以是其他输入函数。

一致前馈回路类型一(C1-FFL)

具有与门的C1-FFL有“符号-敏感延迟”单元和持久性探测器的功能，这一点在大肠杆菌阿拉伯糖系系统的理论^[44]和实验上^[46] 都有发现。这意味着该模体可以提供脉冲过滤，短脉冲信号不会产生响应，而持久信号在短延迟后会产生响应。当持久脉冲结束时，输出的关闭将很快。与此相反的行为出现在具有快速响应和延迟关闭特性的加和门的情况下，这在大肠杆菌的鞭毛系统中得到了证明。^[47]在基因调控网络的重头进化中，对于滤除理想化的短信号脉冲作为进化压，C1-FFLs已经在计算上被证明可以进化出来。但是对于非理想化的噪声，不同拓扑结构前馈调节的动态系统将被优先考虑。 ^[48]

非一致前馈回路类型一(I1-FFL)

I1-FFL是一个脉冲生成器和响应加速器。I1-FFL的两种信号通路作用方向相反，一种通路激活Z，而另一种抑制Z。完全的抑制会导致类似脉冲的动力学行为。另外有实验证明，它可以类似于NAR模体起到响应加速器的作用。与NAR模体的不同之处在于，它可以加速任何基因的响应，而不必是转录因子。^[49]I1-FFL网络还有另外一个功能：在理论和实验上都有证明I1-FFL可以生成非单调的输入函数，无论在人工合成的^[50]还是自然的系统中。 ^[51] 最后，包含非一致前馈调控的基因生成物的表达单元对DNA模板的数量具有适应性，可以优于简单的组合本构启动子。^[52] 前馈调控比负反馈具有更好的适应性，并且基于RNA干扰的网络对DNA模板数具有最高的鲁棒性。^[52]

多输出前馈回路

在某些情况，相同的调控子X和Y可以调控同一系统中的多个Z基因。通过调节相互作用的强度，这些网络可以决定基因激活的时间顺序。这一点在大肠杆菌的鞭毛系统中有实验证据。^[53]

单一输入模块(SIM)

当单个调控子调控一组基因，并且没有其他的调控因素时，这样的模体叫做单一输入模块（SIM）。当很多基因合作执行某个功能时这是有用的，因为这些基因需要同步地被激活。通过调节相互作用的强度，可以编排它所调控的基因表达的时间顺序。^[54]

在文献中，多输入模块（MIM）来自于SIM的扩展。但是二者的精确定义并不太一致。有一些尝试给出生物网络中规范模体的正交定义，也有一些算法去枚举它们，特别是SIM，MIM和2x2 MIM等。^[55]

密集交盖调节网(DOR)

这种类型的网络存在于多个调节子结合起来控制一组基因的情形，并且有多种调控的组合。这种模体出现在大肠杆菌的多种系统中，例如碳利用、厌氧生长、应激反应等。^[17]^[22] 为了更好地理解这种网络，我们必须得到关于基因集成多种输入的方式的信息。Kaplan et al.^[56]绘制了大肠杆菌糖利用基因的输入函数，表现出各种各样的形状。

活动模体

有一个对网络模体的有趣概括：活动模体是在对节点和边都被量化标注的网络中可发现的【反复】斑图。例如，当新陈代谢的边以相应基因的表达量或【时间】来标注时，一些斑图在给定的底层网络结构里【是反复的】。^[57]

批判

对拓扑子结构有一个（某种程度上隐含的）前提性假设是其具有特定的功能重要性。但该假设最近遭到质疑，有人提出在不同的网络环境下模体可能表现出多样性，例如双扇模体，故^[58]模体的结构不必然决定功能，网络结构也不当然能揭示其功能；这种见解由来已久，可参见操纵子。^[59]

大多数模体功能分析是基于模体孤立运行的情形。最近的研究^[60]表明网络环境至关重要，不能忽视网络环境而仅从本地结构来对其功能进行推论——引用的论文还回顾了对观测数据的批判及其他可能的解释。人们研究了单个模体模组对网络全局的动力学影响及其分析^[61]。而另一项近期的研究工作提出生物网络的某些拓扑特征能自然地引起经典模体的常见形态，让人不禁疑问：这样的发生频率是否能证明模体的结构是出于其对所在网络运行的功能性贡献而被选择保留下的结果？^[62]^[63]

模体的研究主要应用于静态复杂网络，而时变复杂网络的研究^[64]就网络模体提出了重大的新解释，并介绍了时变网络模体的概念。Braha和Bar-Yam^[65]研究了本地模体结构在时间依赖网络/时变网络的动力学，发现的一些反复模式有望成为社会互动周期的经验论据。他们证明了对于时变网络，其本地结构是时间依赖的且可能随时间演变，可作为对复杂网络中稳定模体观及模体表达观的反论，Braha和Bar-Yam还进一步提出，对时变本地结构的分析有可能揭示系统级任务和功能方面的动力学的重要信息。

另参

参考文献

↑ Masoudi-Nejad A, Schreiber F, Razaghi MK Z (2012). "Building Blocks of Biological Networks: A Review on Major Network Motif Discovery Algorithms". IET Systems Biology. 6 (5): 164–74. doi:10.1049/iet-syb.2011.0011. PMID 23101871.
↑ Diestel R (2005). "Graph Theory (Graduate Texts in Mathematics)". 173. New York: Springer-Verlag Heidelberg. {{cite journal}}: Cite journal requires |journal= (help)
↑ ^3.0 ^3.1 Milo R, Shen-Orr SS, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (2002). "Network motifs: simple building blocks of complex networks". Science. 298 (5594): 824–827. Bibcode:2002Sci...298..824M. CiteSeerX 10.1.1.225.8750. doi:10.1126/science.298.5594.824. PMID 12399590.
↑ Albert R, Barabási AL (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–49. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. CiteSeerX 10.1.1.242.4753. doi:10.1103/RevModPhys.74.47.
↑ ^5.0 ^5.1 Milo R, Itzkovitz S, Kashtan N, Levitt R, Shen-Orr S, Ayzenshtat I, Sheffer M, Alon U (2004). "Superfamilies of designed and evolved networks". Science. 303 (5663): 1538–1542. Bibcode:2004Sci...303.1538M. doi:10.1126/science.1089167. PMID 15001784.
↑ ^6.0 ^6.1 Schwöbbermeyer, H (2008). "Network Motifs". In Junker BH, Schreiber F (ed.). Analysis of Biological Networks. Hoboken, New Jersey: John Wiley & Sons. pp. 85–108.
↑ Bornholdt, S; Schuster, HG (2003). "Handbook of graphs and networks : from the genome to the Internet". Handbook of Graphs and Networks: From the Genome to the Internet. p. 417. Bibcode:2003hgnf.book.....B.
↑ ^8.0 ^8.1 Ciriello G, Guerra C (2008). "A review on models and algorithms for motif discovery in protein-protein interaction networks". Briefings in Functional Genomics and Proteomics. 7 (2): 147–156. doi:10.1093/bfgp/eln015. PMID 18443014.
↑ ^9.0 ^9.1 ^9.2 ^9.3 ^9.4 ^9.5 Kashtan N, Itzkovitz S, Milo R, Alon U (2004). "Efficient sampling algorithm for estimating sub-graph concentrations and detecting network motifs". Bioinformatics. 20 (11): 1746–1758. doi:10.1093/bioinformatics/bth163. PMID 15001476.
↑ ^10.0 ^10.1 ^10.2 ^10.3 Wernicke S (2006). "Efficient detection of network motifs". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 3 (4): 347–359. CiteSeerX 10.1.1.304.2576. doi:10.1109/tcbb.2006.51. PMID 17085844.
↑ Picard F, Daudin JJ, Schbath S, Robin S (2005). "Assessing the Exceptionality of Network Motifs". J. Comp. Bio. 15 (1): 1–20. CiteSeerX 10.1.1.475.4300. doi:10.1089/cmb.2007.0137. PMID 18257674.
↑ ^12.0 ^12.1 ^12.2 Frequency concepts and pattern detection for the analysis of motifs in networks. Lecture Notes in Computer Science. 3737. 2005. pp. 89–104. doi:10.1007/11599128_7. ISBN 978-3-540-30883-6.
↑ Holland, P. W., & Leinhardt, S. (1974). The statistical analysis of local structure in social networks. Working Paper No. 44, National Bureau of Economic Research.
↑ Hollandi, P., & Leinhardt, S. (1975). The Statistical Analysis of Local. Structure in Social Networks. Sociological Methodology, David Heise, ed. San Francisco: Josey-Bass.
↑ Holland, P. W., & Leinhardt, S. (1976). Local structure in social networks. Sociological methodology, 7, 1-45.
↑ Holland, P. W., & Leinhardt, S. (1977). A method for detecting structure in sociometric data. In Social Networks (pp. 411-432). Academic Press.
↑ ^17.0 ^17.1 ^17.2 Shen-Orr SS, Milo R, Mangan S, Alon U (May 2002). "Network motifs in the transcriptional regulation network of Escherichia coli". Nat. Genet. 31 (1): 64–8. doi:10.1038/ng881. PMID 11967538.
↑ Eichenberger P, Fujita M, Jensen ST, et al. (October 2004). "The program of gene transcription for a single differentiating cell type during sporulation in Bacillus subtilis". PLOS Biology. 2 (10): e328. doi:10.1371/journal.pbio.0020328. PMC 517825. PMID 15383836.
↑ Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (October 2002). "Network motifs: simple building blocks of complex networks". Science. 298 (5594): 824–7. Bibcode:2002Sci...298..824M. CiteSeerX 10.1.1.225.8750. doi:10.1126/science.298.5594.824. PMID 12399590.
↑ Lee TI, Rinaldi NJ, Robert F, et al. (October 2002). "Transcriptional regulatory networks in Saccharomyces cerevisiae". Science. 298 (5594): 799–804. Bibcode:2002Sci...298..799L. doi:10.1126/science.1075090. PMID 12399584.
↑ Odom DT, Zizlsperger N, Gordon DB, et al. (February 2004). "Control of pancreas and liver gene expression by HNF transcription factors". Science. 303 (5662): 1378–81. Bibcode:2004Sci...303.1378O. doi:10.1126/science.1089769. PMC 3012624. PMID 14988562.
↑ ^22.0 ^22.1 Boyer LA, Lee TI, Cole MF, et al. (September 2005). "Core transcriptional regulatory circuitry in human embryonic stem cells". Cell. 122 (6): 947–56. doi:10.1016/j.cell.2005.08.020. PMC 3006442. PMID 16153702.
↑ Iranfar N, Fuller D, Loomis WF (February 2006). "Transcriptional regulation of post-aggregation genes in Dictyostelium by a feed-forward loop involving GBF and LagC". Dev. Biol. 290 (2): 460–9. doi:10.1016/j.ydbio.2005.11.035. PMID 16386729.
↑ Ma'ayan A, Jenkins SL, Neves S, et al. (August 2005). "Formation of regulatory patterns during signal propagation in a Mammalian cellular network". Science. 309 (5737): 1078–83. Bibcode:2005Sci...309.1078M. doi:10.1126/science.1108876. PMC 3032439. PMID 16099987.
↑ Ptacek J, Devgan G, Michaud G, et al. (December 2005). "Global analysis of protein phosphorylation in yeast" (PDF). Nature (Submitted manuscript). 438 (7068): 679–84. Bibcode:2005Natur.438..679P. doi:10.1038/nature04187. PMID 16319894.
↑ "Acc-Motif: Accelerated Motif Detection".
↑ Schreiber F, Schwobbermeyer H (2005). "MAVisto: a tool for the exploration of network motifs". Bioinformatics. 21 (17): 3572–3574. doi:10.1093/bioinformatics/bti556. PMID 16020473.
↑ McKay BD (1981). "Practical graph isomorphism". Congressus Numerantium. 30: 45–87. arXiv:1301.1493. Bibcode:2013arXiv1301.1493M.
↑ McKay BD (1998). "Isomorph-free exhaustive generation". Journal of Algorithms. 26 (2): 306–324. doi:10.1006/jagm.1997.0898.
↑ ^30.0 ^30.1 ^30.2 ^30.3 Ribeiro P, Silva F (2010). G-Tries: an efficient data structure for discovering network motifs. ACM 25th Symposium On Applied Computing - Bioinformatics Track. Sierre, Switzerland. pp. 1559–1566.
↑ ^31.0 ^31.1 Omidi S, Schreiber F, Masoudi-Nejad A (2009). "MODA: an efficient algorithm for network motif discovery in biological networks". Genes Genet Syst. 84 (5): 385–395. doi:10.1266/ggs.84.385. PMID 20154426.
↑ ^32.0 ^32.1 Kashani ZR, Ahrabian H, Elahi E, Nowzari-Dalini A, Ansari ES, Asadi S, Mohammadi S, Schreiber F, Masoudi-Nejad A (2009). "Kavosh: a new algorithm for finding network motifs". BMC Bioinformatics. 10 (318): 318. doi:10.1186/1471-2105-10-318. PMC 2765973. PMID 19799800.
↑ ^33.0 ^33.1 Babu MM, Luscombe NM, Aravind L, Gerstein M, Teichmann SA (June 2004). "Structure and evolution of transcriptional regulatory networks". Current Opinion in Structural Biology. 14 (3): 283–91. CiteSeerX 10.1.1.471.9692. doi:10.1016/j.sbi.2004.05.004. PMID 15193307.
↑ ^34.0 ^34.1 Conant GC, Wagner A (July 2003). "Convergent evolution of gene circuits". Nat. Genet. 34 (3): 264–6. doi:10.1038/ng1181. PMID 12819781.
↑ Dekel E, Alon U (July 2005). "Optimality and evolutionary tuning of the expression level of a protein". Nature. 436 (7050): 588–92. Bibcode:2005Natur.436..588D. doi:10.1038/nature03842. PMID 16049495.
↑ Zabet NR (September 2011). "Negative feedback and physical limits of genes". Journal of Theoretical Biology. 284 (1): 82–91. arXiv:1408.1869. CiteSeerX 10.1.1.759.5418. doi:10.1016/j.jtbi.2011.06.021. PMID 21723295.
↑ Rosenfeld N, Elowitz MB, Alon U (November 2002). "Negative autoregulation speeds the response times of transcription networks". J. Mol. Biol. 323 (5): 785–93. CiteSeerX 10.1.1.126.2604. doi:10.1016/S0022-2836(02)00994-4. PMID 12417193.
↑ Camas FM, Blázquez J, Poyatos JF (August 2006). "Autogenous and nonautogenous control of response in a genetic network". Proc. Natl. Acad. Sci. U.S.A. 103 (34): 12718–23. Bibcode:2006PNAS..10312718C. doi:10.1073/pnas.0602119103. PMC 1568915. PMID 16908855.
↑ Becskei A, Serrano L (June 2000). "Engineering stability in gene networks by autoregulation". Nature. 405 (6786): 590–3. doi:10.1038/35014651. PMID 10850721.
↑ Dublanche Y, Michalodimitrakis K, Kümmerer N, Foglierini M, Serrano L (2006). "Noise in transcription negative feedback loops: simulation and experimental analysis". Mol. Syst. Biol. 2 (1): 41. doi:10.1038/msb4100081. PMC 1681513. PMID 16883354.
↑ Shimoga V, White J, Li Y, Sontag E, Bleris L (2013). "Synthetic mammalian transgene negative autoregulation". Mol. Syst. Biol. 9: 670. doi:10.1038/msb.2013.27. PMC 3964311. PMID 23736683.
↑ Maeda YT, Sano M (June 2006). "Regulatory dynamics of synthetic gene networks with positive feedback". J. Mol. Biol. 359 (4): 1107–24. doi:10.1016/j.jmb.2006.03.064. PMID 16701695.
↑ Becskei A, Séraphin B, Serrano L (May 2001). "Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion". EMBO J. 20 (10): 2528–35. doi:10.1093/emboj/20.10.2528. PMC 125456. PMID 11350942.
↑ ^44.0 ^44.1 ^44.2 Mangan S, Alon U (October 2003). "Structure and function of the feed-forward loop network motif". Proc. Natl. Acad. Sci. U.S.A. 100 (21): 11980–5. Bibcode:2003PNAS..10011980M. doi:10.1073/pnas.2133841100. PMC 218699. PMID 14530388.
↑ Ma HW, Kumar B, Ditges U, Gunzer F, Buer J, Zeng AP (2004). "An extended transcriptional regulatory network of Escherichia coli and analysis of its hierarchical structure and network motifs". Nucleic Acids Res. 32 (22): 6643–9. doi:10.1093/nar/gkh1009. PMC 545451. PMID 15604458.
↑ Mangan S, Zaslaver A, Alon U (November 2003). "The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks". J. Mol. Biol. 334 (2): 197–204. CiteSeerX 10.1.1.110.4629. doi:10.1016/j.jmb.2003.09.049. PMID 14607112.
↑ Kalir S, Mangan S, Alon U (2005). "A coherent feed-forward loop with a SUM input function prolongs flagella expression in Escherichia coli". Mol. Syst. Biol. 1 (1): E1–E6. doi:10.1038/msb4100010. PMC 1681456. PMID 16729041.
↑ Xiong, Kun; Lancaster, Alex K.; Siegal, Mark L.; Masel, Joanna (3 June 2019). "Feed-forward regulation adaptively evolves via dynamics rather than topology when there is intrinsic noise". Nature Communications. 10 (1): 2418. doi:10.1038/s41467-019-10388-6. PMC 6546794. PMID 31160574.
↑ Mangan S, Itzkovitz S, Zaslaver A, Alon U (March 2006). "The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli". J. Mol. Biol. 356 (5): 1073–81. CiteSeerX 10.1.1.184.8360. doi:10.1016/j.jmb.2005.12.003. PMID 16406067.
↑ Entus R, Aufderheide B, Sauro HM (August 2007). "Design and implementation of three incoherent feed-forward motif based biological concentration sensors". Syst Synth Biol. 1 (3): 119–28. doi:10.1007/s11693-007-9008-6. PMC 2398716. PMID 19003446.
↑ Kaplan S, Bren A, Dekel E, Alon U (2008). "The incoherent feed-forward loop can generate non-monotonic input functions for genes". Mol. Syst. Biol. 4 (1): 203. doi:10.1038/msb.2008.43. PMC 2516365. PMID 18628744.
↑ ^52.0 ^52.1 Bleris L, Xie Z, Glass D, Adadey A, Sontag E, Benenson Y (2011). "Synthetic incoherent feedforward circuits show adaptation to the amount of their genetic template". Mol. Syst. Biol. 7 (1): 519. doi:10.1038/msb.2011.49. PMC 3202791. PMID 21811230.
↑ Kalir S, McClure J, Pabbaraju K, et al. (June 2001). "Ordering genes in a flagella pathway by analysis of expression kinetics from living bacteria". Science. 292 (5524): 2080–3. doi:10.1126/science.1058758. PMID 11408658.
↑ Zaslaver A, Mayo AE, Rosenberg R, et al. (May 2004). "Just-in-time transcription program in metabolic pathways". Nat. Genet. 36 (5): 486–91. doi:10.1038/ng1348. PMID 15107854.
↑ Konagurthu AS, Lesk AM (2008). "Single and Multiple Input Modules in regulatory networks". Proteins. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061.
↑ Kaplan S, Bren A, Zaslaver A, Dekel E, Alon U (March 2008). "Diverse two-dimensional input functions control bacterial sugar genes". Mol. Cell. 29 (6): 786–92. doi:10.1016/j.molcel.2008.01.021. PMC 2366073. PMID 18374652.
↑ Chechik G, Oh E, Rando O, Weissman J, Regev A, Koller D (November 2008). "Activity motifs reveal principles of timing in transcriptional control of the yeast metabolic network". Nat. Biotechnol. 26 (11): 1251–9. doi:10.1038/nbt.1499. PMC 2651818. PMID 18953355.
↑ Ingram PJ, Stumpf MP, Stark J (2006). "Network motifs: structure does not determine function". BMC Genomics. 7: 108. doi:10.1186/1471-2164-7-108. PMC 1488845. PMID 16677373.
↑ Voigt CA, Wolf DM, Arkin AP (March 2005). "The Bacillus subtilis sin operon: an evolvable network motif". Genetics. 169 (3): 1187–202. doi:10.1534/genetics.104.031955. PMC 1449569. PMID 15466432.
↑ Knabe JF, Nehaniv CL, Schilstra MJ (2008). "Do motifs reflect evolved function?—No convergent evolution of genetic regulatory network subgraph topologies". BioSystems. 94 (1–2): 68–74. doi:10.1016/j.biosystems.2008.05.012. PMID 18611431.
↑ Taylor D, Restrepo JG (2011). "Network connectivity during mergers and growth: Optimizing the addition of a module". Physical Review E. 83 (6): 66112. arXiv:1102.4876. Bibcode:2011PhRvE..83f6112T. doi:10.1103/PhysRevE.83.066112. PMID 21797446.
↑ Konagurthu, Arun S.; Lesk, Arthur M. (23 April 2008). "Single and multiple input modules in regulatory networks". Proteins: Structure, Function, and Bioinformatics. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061.
↑ Konagurthu AS, Lesk AM (2008). "On the origin of distribution patterns of motifs in biological networks". BMC Syst Biol. 2: 73. doi:10.1186/1752-0509-2-73. PMC 2538512. PMID 18700017.
↑ Braha, D., & Bar‐Yam, Y. (2006). From centrality to temporary fame: Dynamic centrality in complex networks. Complexity, 12(2), 59-63.
↑ Braha D., Bar-Yam Y. (2009) Time-Dependent Complex Networks: Dynamic Centrality, Dynamic Motifs, and Cycles of Social Interactions. In: Gross T., Sayama H. (eds) Adaptive Networks. Understanding Complex Systems. Springer, Berlin, Heidelberg

外部链接

编者推荐

Science经典：复杂网络的简单构造模块——网络模体

集智相关文章

Science经典：复杂网络的简单构造模块——网络模体

模体（motif）是一个对初涉复杂科学的人来说，相对陌生的概念，但它却是复杂网络研究中最有力的工具之一。2002年的 Science 论文“Network Motifs: simple Building blocks of Complex Networks”介绍了模体的概念，至今引用次数已有 6000 多次。本文将概述这篇论文，并阐述模体在复杂网络中的广泛应用与研究前沿，说明模体已成为复杂网络研究中不可或缺的基础组件。即使对于非相关领域的研究者，理解模体的概念也可以让你体会生活中的复杂性与涌现现象。

本中文词条由Xebec、木子二月鸟、Qige96、Jxzhou、厚朴参与编译、由Imp审校、薄荷编辑，欢迎在讨论页面留言。

本词条内容翻译自 wikipedia.org，遵守 CC3.0协议。

[mas1-1] Masoudi-Nejad A, Schreiber F, Razaghi MK Z (2012). "Building Blocks of Biological Networks: A Review on Major Network Motif Discovery Algorithms". IET Systems Biology. 6 (5): 164–74. doi:10.1049/iet-syb.2011.0011. PMID 23101871.

[die1-2] Diestel R (2005). "Graph Theory (Graduate Texts in Mathematics)". 173. New York: Springer-Verlag Heidelberg. {{cite journal}}: Cite journal requires |journal= (help)

[mil1-3] 3.0 ^3.1 Milo R, Shen-Orr SS, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (2002). "Network motifs: simple building blocks of complex networks". Science. 298 (5594): 824–827. Bibcode:2002Sci...298..824M. CiteSeerX 10.1.1.225.8750. doi:10.1126/science.298.5594.824. PMID 12399590.

[alb1-4] Albert R, Barabási AL (2002). "Statistical mechanics of complex networks". Reviews of Modern Physics. 74 (1): 47–49. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. CiteSeerX 10.1.1.242.4753. doi:10.1103/RevModPhys.74.47.

[mil2-5] 5.0 ^5.1 Milo R, Itzkovitz S, Kashtan N, Levitt R, Shen-Orr S, Ayzenshtat I, Sheffer M, Alon U (2004). "Superfamilies of designed and evolved networks". Science. 303 (5663): 1538–1542. Bibcode:2004Sci...303.1538M. doi:10.1126/science.1089167. PMID 15001784.

[sch1-6] 6.0 ^6.1 Schwöbbermeyer, H (2008). "Network Motifs". In Junker BH, Schreiber F (ed.). Analysis of Biological Networks. Hoboken, New Jersey: John Wiley & Sons. pp. 85–108.

[bor1-7] Bornholdt, S; Schuster, HG (2003). "Handbook of graphs and networks : from the genome to the Internet". Handbook of Graphs and Networks: From the Genome to the Internet. p. 417. Bibcode:2003hgnf.book.....B.

[cir1-8] 8.0 ^8.1 Ciriello G, Guerra C (2008). "A review on models and algorithms for motif discovery in protein-protein interaction networks". Briefings in Functional Genomics and Proteomics. 7 (2): 147–156. doi:10.1093/bfgp/eln015. PMID 18443014.

[kas1-9] 9.0 ^9.1 ^9.2 ^9.3 ^9.4 ^9.5 Kashtan N, Itzkovitz S, Milo R, Alon U (2004). "Efficient sampling algorithm for estimating sub-graph concentrations and detecting network motifs". Bioinformatics. 20 (11): 1746–1758. doi:10.1093/bioinformatics/bth163. PMID 15001476.

[wer1-10] 10.0 ^10.1 ^10.2 ^10.3 Wernicke S (2006). "Efficient detection of network motifs". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 3 (4): 347–359. CiteSeerX 10.1.1.304.2576. doi:10.1109/tcbb.2006.51. PMID 17085844.

[pic1-11] Picard F, Daudin JJ, Schbath S, Robin S (2005). "Assessing the Exceptionality of Network Motifs". J. Comp. Bio. 15 (1): 1–20. CiteSeerX 10.1.1.475.4300. doi:10.1089/cmb.2007.0137. PMID 18257674.

[schr1-12] 12.0 ^12.1 ^12.2 Frequency concepts and pattern detection for the analysis of motifs in networks. Lecture Notes in Computer Science. 3737. 2005. pp. 89–104. doi:10.1007/11599128_7. ISBN 978-3-540-30883-6.

[13] Holland, P. W., & Leinhardt, S. (1974). The statistical analysis of local structure in social networks. Working Paper No. 44, National Bureau of Economic Research.

[14] Hollandi, P., & Leinhardt, S. (1975). The Statistical Analysis of Local. Structure in Social Networks. Sociological Methodology, David Heise, ed. San Francisco: Josey-Bass.

[15] Holland, P. W., & Leinhardt, S. (1976). Local structure in social networks. Sociological methodology, 7, 1-45.

[16] Holland, P. W., & Leinhardt, S. (1977). A method for detecting structure in sociometric data. In Social Networks (pp. 411-432). Academic Press.

[she1-17] 17.0 ^17.1 ^17.2 Shen-Orr SS, Milo R, Mangan S, Alon U (May 2002). "Network motifs in the transcriptional regulation network of Escherichia coli". Nat. Genet. 31 (1): 64–8. doi:10.1038/ng881. PMID 11967538.

[eic1-18] Eichenberger P, Fujita M, Jensen ST, et al. (October 2004). "The program of gene transcription for a single differentiating cell type during sporulation in Bacillus subtilis". PLOS Biology. 2 (10): e328. doi:10.1371/journal.pbio.0020328. PMC 517825. PMID 15383836.

[mil3-19] Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (October 2002). "Network motifs: simple building blocks of complex networks". Science. 298 (5594): 824–7. Bibcode:2002Sci...298..824M. CiteSeerX 10.1.1.225.8750. doi:10.1126/science.298.5594.824. PMID 12399590.

[lee1-20] Lee TI, Rinaldi NJ, Robert F, et al. (October 2002). "Transcriptional regulatory networks in Saccharomyces cerevisiae". Science. 298 (5594): 799–804. Bibcode:2002Sci...298..799L. doi:10.1126/science.1075090. PMID 12399584.

[odo1-21] Odom DT, Zizlsperger N, Gordon DB, et al. (February 2004). "Control of pancreas and liver gene expression by HNF transcription factors". Science. 303 (5662): 1378–81. Bibcode:2004Sci...303.1378O. doi:10.1126/science.1089769. PMC 3012624. PMID 14988562.

[boy1-22] 22.0 ^22.1 Boyer LA, Lee TI, Cole MF, et al. (September 2005). "Core transcriptional regulatory circuitry in human embryonic stem cells". Cell. 122 (6): 947–56. doi:10.1016/j.cell.2005.08.020. PMC 3006442. PMID 16153702.

[ira1-23] Iranfar N, Fuller D, Loomis WF (February 2006). "Transcriptional regulation of post-aggregation genes in Dictyostelium by a feed-forward loop involving GBF and LagC". Dev. Biol. 290 (2): 460–9. doi:10.1016/j.ydbio.2005.11.035. PMID 16386729.

[maa1-24] Ma'ayan A, Jenkins SL, Neves S, et al. (August 2005). "Formation of regulatory patterns during signal propagation in a Mammalian cellular network". Science. 309 (5737): 1078–83. Bibcode:2005Sci...309.1078M. doi:10.1126/science.1108876. PMC 3032439. PMID 16099987.

[pta1-25] Ptacek J, Devgan G, Michaud G, et al. (December 2005). "Global analysis of protein phosphorylation in yeast" (PDF). Nature (Submitted manuscript). 438 (7068): 679–84. Bibcode:2005Natur.438..679P. doi:10.1038/nature04187. PMID 16319894.

[26] "Acc-Motif: Accelerated Motif Detection".

[schr2-27] Schreiber F, Schwobbermeyer H (2005). "MAVisto: a tool for the exploration of network motifs". Bioinformatics. 21 (17): 3572–3574. doi:10.1093/bioinformatics/bti556. PMID 16020473.

[mck1-28] McKay BD (1981). "Practical graph isomorphism". Congressus Numerantium. 30: 45–87. arXiv:1301.1493. Bibcode:2013arXiv1301.1493M.

[mck2-29] McKay BD (1998). "Isomorph-free exhaustive generation". Journal of Algorithms. 26 (2): 306–324. doi:10.1006/jagm.1997.0898.

[rib1-30] 30.0 ^30.1 ^30.2 ^30.3 Ribeiro P, Silva F (2010). G-Tries: an efficient data structure for discovering network motifs. ACM 25th Symposium On Applied Computing - Bioinformatics Track. Sierre, Switzerland. pp. 1559–1566.

[omi1-31] 31.0 ^31.1 Omidi S, Schreiber F, Masoudi-Nejad A (2009). "MODA: an efficient algorithm for network motif discovery in biological networks". Genes Genet Syst. 84 (5): 385–395. doi:10.1266/ggs.84.385. PMID 20154426.

[kash1-32] 32.0 ^32.1 Kashani ZR, Ahrabian H, Elahi E, Nowzari-Dalini A, Ansari ES, Asadi S, Mohammadi S, Schreiber F, Masoudi-Nejad A (2009). "Kavosh: a new algorithm for finding network motifs". BMC Bioinformatics. 10 (318): 318. doi:10.1186/1471-2105-10-318. PMC 2765973. PMID 19799800.

[bab1-33] 33.0 ^33.1 Babu MM, Luscombe NM, Aravind L, Gerstein M, Teichmann SA (June 2004). "Structure and evolution of transcriptional regulatory networks". Current Opinion in Structural Biology. 14 (3): 283–91. CiteSeerX 10.1.1.471.9692. doi:10.1016/j.sbi.2004.05.004. PMID 15193307.

[con1-34] 34.0 ^34.1 Conant GC, Wagner A (July 2003). "Convergent evolution of gene circuits". Nat. Genet. 34 (3): 264–6. doi:10.1038/ng1181. PMID 12819781.

[dek1-35] Dekel E, Alon U (July 2005). "Optimality and evolutionary tuning of the expression level of a protein". Nature. 436 (7050): 588–92. Bibcode:2005Natur.436..588D. doi:10.1038/nature03842. PMID 16049495.

[zab1-36] Zabet NR (September 2011). "Negative feedback and physical limits of genes". Journal of Theoretical Biology. 284 (1): 82–91. arXiv:1408.1869. CiteSeerX 10.1.1.759.5418. doi:10.1016/j.jtbi.2011.06.021. PMID 21723295.

[ros1-37] Rosenfeld N, Elowitz MB, Alon U (November 2002). "Negative autoregulation speeds the response times of transcription networks". J. Mol. Biol. 323 (5): 785–93. CiteSeerX 10.1.1.126.2604. doi:10.1016/S0022-2836(02)00994-4. PMID 12417193.

[cam1-38] Camas FM, Blázquez J, Poyatos JF (August 2006). "Autogenous and nonautogenous control of response in a genetic network". Proc. Natl. Acad. Sci. U.S.A. 103 (34): 12718–23. Bibcode:2006PNAS..10312718C. doi:10.1073/pnas.0602119103. PMC 1568915. PMID 16908855.

[bec1-39] Becskei A, Serrano L (June 2000). "Engineering stability in gene networks by autoregulation". Nature. 405 (6786): 590–3. doi:10.1038/35014651. PMID 10850721.

[dub1-40] Dublanche Y, Michalodimitrakis K, Kümmerer N, Foglierini M, Serrano L (2006). "Noise in transcription negative feedback loops: simulation and experimental analysis". Mol. Syst. Biol. 2 (1): 41. doi:10.1038/msb4100081. PMC 1681513. PMID 16883354.

[shi1-41] Shimoga V, White J, Li Y, Sontag E, Bleris L (2013). "Synthetic mammalian transgene negative autoregulation". Mol. Syst. Biol. 9: 670. doi:10.1038/msb.2013.27. PMC 3964311. PMID 23736683.

[mae1-42] Maeda YT, Sano M (June 2006). "Regulatory dynamics of synthetic gene networks with positive feedback". J. Mol. Biol. 359 (4): 1107–24. doi:10.1016/j.jmb.2006.03.064. PMID 16701695.

[bec2-43] Becskei A, Séraphin B, Serrano L (May 2001). "Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion". EMBO J. 20 (10): 2528–35. doi:10.1093/emboj/20.10.2528. PMC 125456. PMID 11350942.

[man1-44] 44.0 ^44.1 ^44.2 Mangan S, Alon U (October 2003). "Structure and function of the feed-forward loop network motif". Proc. Natl. Acad. Sci. U.S.A. 100 (21): 11980–5. Bibcode:2003PNAS..10011980M. doi:10.1073/pnas.2133841100. PMC 218699. PMID 14530388.

[ma1-45] Ma HW, Kumar B, Ditges U, Gunzer F, Buer J, Zeng AP (2004). "An extended transcriptional regulatory network of Escherichia coli and analysis of its hierarchical structure and network motifs". Nucleic Acids Res. 32 (22): 6643–9. doi:10.1093/nar/gkh1009. PMC 545451. PMID 15604458.

[man2-46] Mangan S, Zaslaver A, Alon U (November 2003). "The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks". J. Mol. Biol. 334 (2): 197–204. CiteSeerX 10.1.1.110.4629. doi:10.1016/j.jmb.2003.09.049. PMID 14607112.

[kal1-47] Kalir S, Mangan S, Alon U (2005). "A coherent feed-forward loop with a SUM input function prolongs flagella expression in Escherichia coli". Mol. Syst. Biol. 1 (1): E1–E6. doi:10.1038/msb4100010. PMC 1681456. PMID 16729041.

[48] Xiong, Kun; Lancaster, Alex K.; Siegal, Mark L.; Masel, Joanna (3 June 2019). "Feed-forward regulation adaptively evolves via dynamics rather than topology when there is intrinsic noise". Nature Communications. 10 (1): 2418. doi:10.1038/s41467-019-10388-6. PMC 6546794. PMID 31160574.

[man3-49] Mangan S, Itzkovitz S, Zaslaver A, Alon U (March 2006). "The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli". J. Mol. Biol. 356 (5): 1073–81. CiteSeerX 10.1.1.184.8360. doi:10.1016/j.jmb.2005.12.003. PMID 16406067.

[ent1-50] Entus R, Aufderheide B, Sauro HM (August 2007). "Design and implementation of three incoherent feed-forward motif based biological concentration sensors". Syst Synth Biol. 1 (3): 119–28. doi:10.1007/s11693-007-9008-6. PMC 2398716. PMID 19003446.

[kap1-51] Kaplan S, Bren A, Dekel E, Alon U (2008). "The incoherent feed-forward loop can generate non-monotonic input functions for genes". Mol. Syst. Biol. 4 (1): 203. doi:10.1038/msb.2008.43. PMC 2516365. PMID 18628744.

[ble1-52] 52.0 ^52.1 Bleris L, Xie Z, Glass D, Adadey A, Sontag E, Benenson Y (2011). "Synthetic incoherent feedforward circuits show adaptation to the amount of their genetic template". Mol. Syst. Biol. 7 (1): 519. doi:10.1038/msb.2011.49. PMC 3202791. PMID 21811230.

[kal2-53] Kalir S, McClure J, Pabbaraju K, et al. (June 2001). "Ordering genes in a flagella pathway by analysis of expression kinetics from living bacteria". Science. 292 (5524): 2080–3. doi:10.1126/science.1058758. PMID 11408658.

[zas1-54] Zaslaver A, Mayo AE, Rosenberg R, et al. (May 2004). "Just-in-time transcription program in metabolic pathways". Nat. Genet. 36 (5): 486–91. doi:10.1038/ng1348. PMID 15107854.

[55] Konagurthu AS, Lesk AM (2008). "Single and Multiple Input Modules in regulatory networks". Proteins. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061.

[kap2-56] Kaplan S, Bren A, Zaslaver A, Dekel E, Alon U (March 2008). "Diverse two-dimensional input functions control bacterial sugar genes". Mol. Cell. 29 (6): 786–92. doi:10.1016/j.molcel.2008.01.021. PMC 2366073. PMID 18374652.

[agc-57] Chechik G, Oh E, Rando O, Weissman J, Regev A, Koller D (November 2008). "Activity motifs reveal principles of timing in transcriptional control of the yeast metabolic network". Nat. Biotechnol. 26 (11): 1251–9. doi:10.1038/nbt.1499. PMC 2651818. PMID 18953355.

[ad-58] Ingram PJ, Stumpf MP, Stark J (2006). "Network motifs: structure does not determine function". BMC Genomics. 7: 108. doi:10.1186/1471-2164-7-108. PMC 1488845. PMID 16677373.

[59] Voigt CA, Wolf DM, Arkin AP (March 2005). "The Bacillus subtilis sin operon: an evolvable network motif". Genetics. 169 (3): 1187–202. doi:10.1534/genetics.104.031955. PMC 1449569. PMID 15466432.

[60] Knabe JF, Nehaniv CL, Schilstra MJ (2008). "Do motifs reflect evolved function?—No convergent evolution of genetic regulatory network subgraph topologies". BioSystems. 94 (1–2): 68–74. doi:10.1016/j.biosystems.2008.05.012. PMID 18611431.

[61] Taylor D, Restrepo JG (2011). "Network connectivity during mergers and growth: Optimizing the addition of a module". Physical Review E. 83 (6): 66112. arXiv:1102.4876. Bibcode:2011PhRvE..83f6112T. doi:10.1103/PhysRevE.83.066112. PMID 21797446.

[62] Konagurthu, Arun S.; Lesk, Arthur M. (23 April 2008). "Single and multiple input modules in regulatory networks". Proteins: Structure, Function, and Bioinformatics. 73 (2): 320–324. doi:10.1002/prot.22053. PMID 18433061.

[63] Konagurthu AS, Lesk AM (2008). "On the origin of distribution patterns of motifs in biological networks". BMC Syst Biol. 2: 73. doi:10.1186/1752-0509-2-73. PMC 2538512. PMID 18700017.

[64] Braha, D., & Bar‐Yam, Y. (2006). From centrality to temporary fame: Dynamic centrality in complex networks. Complexity, 12(2), 59-63.

[65] Braha D., Bar-Yam Y. (2009) Time-Dependent Complex Networks: Dynamic Centrality, Dynamic Motifs, and Cycles of Social Interactions. In: Gross T., Sayama H. (eds) Adaptive Networks. Understanding Complex Systems. Springer, Berlin, Heidelberg

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

“网络模体”的版本间的差异

2020年5月11日 (一) 08:24的版本

目录

定义

历史

模体发现算法

mfinder 算法

FPF (Mavisto)算法

ESU (FANMOD)算法及对应的软件

G-Tries

对比

算法的分类

已知的模体及其功能

负自反馈调控(NAR)

正自反馈调控(PAR)

前馈回路 (FFL)

一致前馈回路类型一(C1-FFL)

非一致前馈回路类型一(I1-FFL)

多输出前馈回路

单一输入模块(SIM)

密集交盖调节网(DOR)

活动模体

批判

另参

参考文献

外部链接

编者推荐

集智相关文章

Science经典：复杂网络的简单构造模块——网络模体

导航菜单

搜索

@@ 第209行： / 第209行： @@
 '''返回'''
 |}
-===NeMoFinder===
-Chen ''et al.'' <ref name="che1">{{cite conference |vauthors=Chen J, Hsu W, Li Lee M, etal |title=NeMoFinder: dissecting genome-wide protein-protein interactions with meso-scale network motifs |conference=the 12th ACM SIGKDD international conference on Knowledge discovery and data mining |year=2006 |location=Philadelphia, Pennsylvania, USA |pages=106–115}}</ref> introduced a new NM discovery algorithm called ''NeMoFinder'', which adapts the idea in ''SPIN'' <ref name="hua1">{{cite conference |vauthors=Huan J, Wang W, Prins J, etal |title=SPIN: mining maximal frequent sub-graphs from graph databases |conference=the 10th ACM SIGKDD international conference on Knowledge discovery and data mining |year=2004 |pages=581–586}}</ref> to extract frequent trees and after that expands them into non-isomorphic graphs.<ref name="cir1" /> ''NeMoFinder'' utilizes frequent size-n trees to partition the input network into a collection of size-{{math|n}} graphs, afterward finding frequent size-n sub-graphs by expansion of frequent trees edge-by-edge until getting a complete size-{{math|n}} graph {{math|K<sub>n</sub>}}. The algorithm finds NMs in undirected networks and is not limited to extracting only induced sub-graphs. Furthermore, ''NeMoFinder'' is an exact enumeration algorithm and is not based on a sampling method. As Chen ''et al.'' claim, ''NeMoFinder'' is applicable for detecting relatively large NMs, for instance, finding NMs up to size-12 from the whole ''S. cerevisiae'' (yeast) PPI network as the authors claimed.<ref name="uet1">{{cite journal |vauthors=Uetz P, Giot L, Cagney G, etal |title=A comprehensive analysis of protein-protein interactions in Saccharomyces cerevisiae |journal=Nature |year=2000 |volume=403 |issue=6770 |pages=623–627 |doi=10.1038/35001009 |pmid=10688190|bibcode=2000Natur.403..623U }}</ref>
-''NeMoFinder'' consists of three main steps. First, finding frequent size-{{math|n}} trees, then utilizing repeated size-n trees to divide the entire network into a collection of size-{{math|n}} graphs, finally, performing sub-graph join operations to find frequent size-n sub-graphs.<ref name="che1" /> In the first step, the algorithm detects all non-isomorphic size-{{math|n}} trees and mappings from a tree to the network. In the second step, the ranges of these mappings are employed to partition the network into size-n graphs. Up to this step, there is no distinction between ''NeMoFinder'' and an exact enumeration method. However, a large portion of non-isomorphic size-n graphs still remain. ''NeMoFinder'' exploits a heuristic to enumerate non-tree size-n graphs by the obtained information from the preceding steps. The main advantage of the algorithm is in the third step, which generates candidate sub-graphs from previously enumerated sub-graphs. This generation of new size-{{math|n}} sub-graphs is done by joining each previous sub-graph with derivative sub-graphs from itself called ''cousin sub-graphs''. These new sub-graphs contain one additional edge in comparison to the previous sub-graphs. However, there exist some problems in generating new sub-graphs: There is no clear method to derive cousins from a graph, joining a sub-graph with its cousins leads to redundancy in generating particular sub-graph more than once, and cousin determination is done by a canonical representation of the adjacency matrix which is not closed under join operation. ''NeMoFinder'' is an efficient network motif finding algorithm for motifs up to size 12 only for protein-protein interaction networks, which are presented as undirected graphs. And it is not able to work on directed networks which are so important in the field of complex and biological networks. The pseudocode of ''NeMoFinder'' is shown below:
-{| class="wikitable"
-|-
-! NeMoFinder
-|-
-|'''Input:'''
-{{math|G}} - PPI network;
-{{math|N}} - Number of randomized networks;
-{{math|K}} - Maximal network motif size;
-{{math|F}} - Frequency threshold;
-{{math|S}} - Uniqueness threshold;
-'''Output:'''
-{{math|U}} - Repeated and unique network motif set;
-{{math|D ← ∅}};
-'''for''' motif-size {{math|k}} '''from''' 3 '''to''' {{math|K}} '''do'''
-{{pad|1em}}{{math|T ← ''FindRepeatedTrees''(k)}};
-{{pad|1em}}{{math|GD<sub>k</sub> ← ''GraphPartition''(G, T)}}
-{{pad|1em}}{{math|D ← D ∪ T}};
-{{pad|1em}}{{math|D&prime; ← T}};
-{{pad|1em}}{{math|i ← k}};
-{{pad|1em}}'''while''' {{math|D&prime; ≠ ∅}} '''and''' {{math|i ≤ k &times; (k - 1) / 2}} '''do'''
-{{pad|2em}}{{math|D&prime; ← ''FindRepeatedGraphs''(k, i, D&prime;)}};
-{{pad|2em}}{{math|D ← D ∪ D&prime;}};
-{{pad|2em}}{{math|i ← i + 1}};
-{{pad|1em}}'''end while'''
-'''end for'''
-'''for''' counter {{math|i}} '''from''' 1 '''to''' {{math|N}} '''do'''
-{{pad|1em}}{{math|G<sub>rand</sub> ← ''RandomizedNetworkGeneration''()}};
-{{pad|1em}}'''for each''' {{math|g ∈ D}} '''do'''
-{{pad|2em}}{{math|''GetRandFrequency''(g, G<sub>rand</sub>)}};
-{{pad|1em}}'''end for'''
-'''end for'''
-{{math|U ← ∅}};
-'''for each''' {{math|g ∈ D}} '''do'''
-{{pad|1em}}{{math|s ← ''GetUniqunessValue''(g)}};
-{{pad|1em}}'''if''' {{math|s ≥ S}} '''then'''
-{{pad|2em}}{{math|U ← U ∪ {g}}};
-{{pad|1em}}'''end if'''
-'''end for'''
-'''return''' {{math|U}};
-|}
-===Grochow–Kellis===
-Grochow and Kellis <ref name="gro1">{{cite conference|vauthors=Grochow JA, Kellis M |title=Network Motif Discovery Using Sub-graph Enumeration and Symmetry-Breaking |conference=RECOMB |year=2007 |pages=92–106| doi=10.1007/978-3-540-71681-5_7| url=http://www.cs.colorado.edu/~jgrochow/Grochow_Kellis_RECOMB_07_Network_Motifs.pdf}}</ref> proposed an ''exact'' algorithm for enumerating sub-graph appearances.   The algorithm is based on a ''motif-centric'' approach, which means that the frequency of a given sub-graph,called the ''query graph'', is exhaustively determined by searching for all possible mappings from the query graph into the larger network. It is claimed <ref name="gro1" /> that a ''motif-centric'' method in comparison to ''network-centric'' methods has some beneficial features. First of all it avoids the increased complexity of sub-graph enumeration. Also, by using mapping instead of enumerating, it enables an improvement in the isomorphism test. To improve the performance of the algorithm, since it is an inefficient exact enumeration algorithm, the authors introduced a fast method which is called ''symmetry-breaking conditions''. During straightforward sub-graph isomorphism tests, a sub-graph may be mapped to the same sub-graph of the query graph multiple times. In the Grochow–Kellis (GK) algorithm symmetry-breaking is used to avoid such multiple mappings. Here we introduce the GK algorithm and the symmetry-breaking condition which eliminates redundant isomorphism tests.
-[[File:Automorphisms of a subgraph.jpg|thumb|(a) ''graph G'', (b) ''illustration of all automorphisms of G that is showed in (a)''. From set AutG we can obtain a set of symmetry-breaking conditions of G given by SymG in (c). Only the first mapping in AutG satisfies the SynG conditions; as a result, by applying SymG in the Isomorphism Extension module the algorithm only enumerate each match-able sub-graph in the network to G once. Note that SynG is not necessarily a unique set for an arbitrary graph G.]]
-The GK algorithm discovers the whole set of mappings of a given query graph to the network in two major steps. It starts with the computation of symmetry-breaking conditions of the query graph. Next, by means of a branch-and-bound method, the algorithm tries to find every possible mapping from the query graph to the network that meets the associated symmetry-breaking conditions. An example of the usage of symmetry-breaking conditions in GK algorithm is demonstrated in figure.
-As it is mentioned above, the symmetry-breaking technique is a simple mechanism that precludes spending time finding a sub-graph more than once due to its symmetries.<ref name="gro1" /><ref name="gro2">{{cite conference|author=Grochow JA |title=On the structure and evolution of protein interaction networks |conference=Thesis M. Eng., Massachusetts Institute of Technology, Dept. of Electrical Engineering and Computer Science|year=2006| url=http://www.cs.toronto.edu/~jgrochow/Grochow_MIT_Masters_06_PPI_Networks.pdf}}</ref> Note that, computing symmetry-breaking conditions requires finding all automorphisms of a given query graph. Even though, there is no efficient (or polynomial time) algorithm for the graph automorphism problem, this problem can be tackled efficiently in practice by McKay's tools.<ref name="mck1" /><ref name="mck2" /> As it is claimed, using symmetry-breaking conditions in NM detection lead to save a great deal of running time. Moreover, it can be inferred from the results in <ref name="gro1" /><ref name="gro2" /> that using the symmetry-breaking conditions results in high efficiency particularly for directed networks in comparison to undirected networks.  The symmetry-breaking conditions used in the GK algorithm are similar to the restriction which ''ESU'' algorithm applies to the labels in EXT and SUB sets. In conclusion, the GK algorithm computes the exact number of appearance of a given query graph in a large complex network and exploiting symmetry-breaking conditions improves the algorithm performance. Also, GK algorithm is one of the known algorithms having no limitation for motif size in implementation and potentially it can find motifs of any size.
-===Color-coding approach===
-Most algorithms in the field of NM discovery are used to find induced sub-graphs of a network. In 2008, Noga Alon ''et al.'' <ref name="alo1">{{cite journal|author1=Alon N |author2=Dao P |author3=Hajirasouliha I |author4=Hormozdiari F |author5=Sahinalp S.C |title=Biomolecular network motif counting and discovery by color coding |journal=Bioinformatics |year=2008 |volume=24 |issue=13 |pages=i241–i249 |doi=10.1093/bioinformatics/btn163|pmid=18586721 |pmc=2718641 }}</ref>  introduced an approach for finding non-induced sub-graphs too. Their technique works on undirected networks such as PPI ones. Also, it counts non-induced trees and bounded treewidth sub-graphs. This method is applied for sub-graphs of size up to 10.
-This algorithm counts the number of non-induced occurrences of a tree {{math|T}} with {{math|k {{=}} O(logn)}} vertices in a network {{math|G}} with {{math|n}} vertices as follows:
-# '''Color coding.''' Color each vertex of input network G independently and uniformly at random with one of the {{math|k}} colors.
-# '''Counting.''' Apply a dynamic programming routine to count the number of non-induced occurrences of {{math|T}} in which each vertex has a unique color. For more details on this step, see.<ref name="alo1" />
-# Repeat the above two steps {{math|O(e<sup>k</sup>)}} times and add up the number of occurrences of {{math|T}} to get an estimate on the number of its occurrences in {{math|G}}.
-As available PPI networks are far from complete and error free, this approach is suitable for NM discovery for such networks. As Grochow–Kellis Algorithm and this one are the ones popular for non-induced sub-graphs, it is worth to mention that the algorithm introduced by Alon ''et al.'' is less time-consuming than the Grochow–Kellis Algorithm.<ref name="alo1" />
-===MODA===
-Omidi ''et al.'' <ref name="omi1">{{cite journal|vauthors=Omidi S, Schreiber F, Masoudi-Nejad A |title=MODA: an efficient algorithm for network motif discovery in biological networks |journal=Genes Genet Syst |year=2009 |volume=84 |issue=5 |pages=385–395 |doi=10.1266/ggs.84.385|pmid=20154426 |doi-access=free }}</ref> introduced a new algorithm for motif detection named ''MODA'' which is applicable for induced and non-induced NM discovery in undirected networks. It is based on the motif-centric approach discussed in the Grochow–Kellis algorithm section. It is very important to distinguish motif-centric algorithms such as MODA and GK algorithm because of their ability to work as query-finding algorithms. This feature allows such algorithms to be able to find a single motif query or a small number of motif queries (not all possible sub-graphs of a given size) with larger sizes. As the number of possible non-isomorphic sub-graphs increases exponentially with sub-graph size, for large size motifs (even larger than 10), the network-centric algorithms, those looking for all possible sub-graphs, face a problem. Although motif-centric algorithms also have problems in discovering all possible large size sub-graphs, but their ability to find small numbers of them is sometimes a significant property.
-Using a hierarchical structure called an ''expansion tree'', the ''MODA'' algorithm is able to extract NMs of a given size systematically and similar to ''FPF'' that avoids enumerating unpromising sub-graphs; ''MODA'' takes into consideration potential queries (or candidate sub-graphs) that would result in frequent sub-graphs. Despite the fact that ''MODA'' resembles ''FPF'' in using a tree like structure, the expansion tree is applicable merely for computing frequency concept {{math|F<sub>1</sub>}}. As we will discuss next, the advantage of this algorithm is that it does not carry out the sub-graph isomorphism test for ''non-tree'' query graphs. Additionally, it utilizes a sampling method in order to speed up the running time of the algorithm.
-Here is the main idea: by a simple criterion one can generalize a mapping of a k-size graph into the network to its same size supergraphs. For example, suppose there is mapping {{math|f(G)}} of graph {{math|G}} with {{math|k}} nodes into the network and we have a same size graph {{math|G&prime;}} with one more edge {{math|&langu, v&rang;}}; {{math|f<sub>G</sub>}} will map {{math|G&prime;}} into the network, if there is an edge {{math|&lang;f<sub>G</sub>(u), f<sub>G</sub>(v)&rang;}} in the network. As a result, we can exploit the mapping set of a graph to determine the frequencies of its same order supergraphs simply in {{math|O(1)}} time without carrying out sub-graph isomorphism testing. The algorithm starts ingeniously with minimally connected query graphs of size k and finds their mappings in the network via sub-graph isomorphism. After that, with conservation of the graph size, it expands previously considered query graphs edge-by-edge and computes the frequency of these expanded graphs as mentioned above. The expansion process continues until reaching a complete graph {{math|K<sub>k</sub>}} (fully connected with {{math|{{frac|k(k-1)|2}}}} edge).
-As discussed above, the algorithm starts by computing sub-tree frequencies in the network and then expands sub-trees edge by edge. One way to implement this idea is called the expansion tree {{math|T<sub>k</sub>}} for each {{math|k}}. Figure shows the expansion tree for size-4 sub-graphs. {{math|T<sub>k</sub>}} organizes the running process and provides query graphs in a hierarchical manner. Strictly speaking, the expansion tree {{math|T<sub>k</sub>}} is simply a [[directed acyclic graph]] or DAG, with its root number {{math|k}} indicating the graph size existing in the expansion tree and each of its other nodes containing the adjacency matrix of a distinct {{math|k}}-size query graph. Nodes in the first level of {{math|T<sub>k</sub>}} are all distinct {{math|k}}-size trees and by traversing {{math|T<sub>k</sub>}} in depth query graphs expand with one edge at each level. A query graph in a node is a sub-graph of the query graph in a node's child with one edge difference. The longest path in {{math|T<sub>k</sub>}} consists of {{math|(k<sup>2</sup>-3k+4)/2}} edges and is the path from the root to the leaf node holding the complete graph. Generating expansion trees can be done by a simple routine which is explained in.<ref name="omi1" />
-''MODA'' traverses {{math|T<sub>k</sub>}} and when it extracts query trees from the first level of {{math|T<sub>k</sub>}} it computes their mapping sets and saves these mappings for the next step. For non-tree queries from {{math|T<sub>k</sub>}}, the algorithm extracts the mappings associated with the parent node in {{math|T<sub>k</sub>}} and determines which of these mappings can support the current query graphs. The process will continue until the algorithm gets the complete query graph. The query tree mappings are extracted using the Grochow–Kellis algorithm. For computing the frequency of non-tree query graphs, the algorithm employs a simple routine that takes {{math|O(1)}} steps. In addition, ''MODA'' exploits a sampling method where the sampling of each node in the network is linearly proportional to the node degree, the probability distribution is exactly similar to the well-known Barabási-Albert preferential attachment model in the field of complex networks.<ref name="bar1">{{cite journal|vauthors=Barabasi AL, Albert R |title=Emergence of scaling in random networks |journal=Science |year=1999 |volume=286 |issue=5439 |pages=509–512 |doi=10.1126/science.286.5439.509 |pmid=10521342|bibcode=1999Sci...286..509B |arxiv=cond-mat/9910332 }}</ref> This approach generates approximations; however, the results are almost stable in different executions since sub-graphs aggregate around highly connected nodes.<ref name="vaz1">{{cite journal |vauthors=Vázquez A, Dobrin R, Sergi D, etal |title=The topological relationship between the large-scale attributes and local interaction patterns of complex networks |journal=PNAS |year=2004 |volume=101 |issue=52 |pages=17940–17945 |doi=10.1073/pnas.0406024101|pmid=15598746 |pmc=539752 |bibcode=2004PNAS..10117940V |arxiv=cond-mat/0408431 }}</ref> The pseudocode of ''MODA'' is shown below:
-[[File:Expansion Tree.jpg|thumb|''Illustration of the expansion tree T4 for 4-node query graphs''. At the first level, there are non-isomorphic k-size trees and at each level, an edge is added to the parent graph to form a child graph. In the second level, there is a graph with two alternative edges that is shown by a dashed red edge. In fact, this node represents two expanded graphs that are isomorphic.<ref name="omi1" />]]
-{| class="wikitable"
-|-
-! MODA
-|-
-|'''Input:''' {{math|G}}: Input graph, {{math|k}}: sub-graph size, {{math|Δ}}: threshold value
-'''Output:''' Frequent Subgraph List: List of all frequent {{math|k}}-size sub-graphs
-'''Note:''' {{math|F<sub>G</sub>}}: set of mappings from {{math|G}} in the input graph {{math|G}}
-'''fetch''' {{math|T<sub>k</sub>}}
-'''do'''
-{{pad|1em}}{{math|G&prime; {{=}} ''Get-Next-BFS''(T<sub>k</sub>)}} // {{math|G&prime;}} is a query graph
-{{pad|1em}}if {{math|{{!}}E(G&prime;){{!}} {{=}} (k – 1)}}
-{{pad|1em}}'''call''' {{math|''Mapping-Module''(G&prime;, G)}}
-{{pad|1em}}'''else'''
-{{pad|2em}}'''call''' {{math|''Enumerating-Module''(G&prime;, G, T<sub>k</sub>)}}
-{{pad|1em}}'''end if'''
-{{pad|1em}}'''save''' {{math|F<sub>2</sub>}}
-{{pad|1em}}'''if''' {{math|{{!}}F<sub>G</sub>{{!}} > Δ}} '''then'''
-{{pad|2em}}add {{math|G&prime;}} into Frequent Subgraph List
-{{pad|1em}}'''end if'''
-'''Until''' {{math|{{!}}E(G'){{!}} {{=}} (k – 1)/2}}
-'''return''' Frequent Subgraph List
-|}
-===Kavosh===
-A recently introduced algorithm named ''Kavosh'' <ref name="kash1">{{cite journal|vauthors=Kashani ZR, Ahrabian H, Elahi E, Nowzari-Dalini A, Ansari ES, Asadi S, Mohammadi S, Schreiber F, Masoudi-Nejad A |title=Kavosh: a new algorithm for finding network motifs |journal=BMC Bioinformatics |year=2009 |volume=10 |issue=318|pages=318 |doi=10.1186/1471-2105-10-318 |pmid=19799800 |pmc=2765973}} {{open access}}</ref> aims at improved main memory usage. ''Kavosh'' is usable to detect NM in both directed and undirected networks. The main idea of the enumeration is similar to the ''GK'' and ''MODA'' algorithms, which first find all {{math|k}}-size sub-graphs that a particular node participated in, then remove the node, and subsequently repeat this process for the remaining nodes.<ref name="kash1" />
-For counting the sub-graphs of size {{math|k}} that include a particular node, trees with maximum depth of k, rooted at this node and based on neighborhood relationship are implicitly built. Children of each node include both incoming and outgoing adjacent nodes. To descend the tree, a child is chosen at each level with the restriction that a particular child can be included only if it has not been included at any upper level. After having descended to the lowest level possible, the tree is again ascended and the process is repeated with the stipulation that nodes visited in earlier paths of a descendant are now considered unvisited nodes. A final restriction in building trees is that all children in a particular tree must have numerical labels larger than the label of the root of the tree. The restrictions on the labels of the children are similar to the conditions which ''GK'' and ''ESU'' algorithm use to avoid overcounting sub-graphs.
-The protocol for extracting sub-graphs makes use of the compositions of an integer. For the extraction of sub-graphs of size {{math|k}}, all possible compositions of the integer {{math|k-1}} must be considered. The compositions of {{math|k-1}} consist of all possible manners of expressing {{math|k-1}} as a sum of positive integers. Summations in which the order of the summands differs are considered distinct. A composition can be expressed as {{math|k<sub>2</sub>,k<sub>3</sub>,…,k<sub>m</sub>}} where {{math|k<sub>2</sub> + k<sub>3</sub> + … + k<sub>m</sub> {{=}} k-1}}. To count sub-graphs based on the composition, {{math|k<sub>i</sub>}} nodes are selected from the {{math|i}}-th level of the tree to be nodes of the sub-graphs ({{math|i {{=}} 2,3,…,m}}). The {{math|k-1}} selected nodes along with the node at the root define a sub-graph within the network. After discovering a sub-graph involved as a match in the target network, in order to be able to evaluate the size of each class according to the target network, ''Kavosh'' employs the ''nauty'' algorithm <ref name="mck1" /><ref name="mck2" /> in the same way as ''FANMOD''. The enumeration part of Kavosh algorithm is shown below:
-{| class="wikitable"
-|-
-! Enumeration of Kavosh
-|-
-|'''''Enumerate_Vertex(G, u, S, Remainder, i)'''''
-'''Input:''' {{math|G}}: Input graph<br>
-{{pad|3em}}{{math|u}}: Root vertex<br>
-{{pad|3em}}{{math|S}}: selection ({{math|S {{=}} { S<sub>0</sub>,S<sub>1</sub>,...,S<sub>k-1</sub>}}} is an array of the set of all {{math|S<sub>i</sub>}})<br>
-{{pad|3em}}{{math|Remainder}}: number of remaining vertices to be selected<br>
-{{pad|3em}}{{math|i}}: Current depth of the tree.<br>
-'''Output:''' all {{math|k}}-size sub-graphs of graph {{math|G}} rooted in {{math|u}}.
-'''if''' {{math|Remainder {{=}} 0}} '''then'''<br>
-{{pad|1em}}'''return'''<br>
-'''else'''<br>
-{{pad|1em}}{{math|ValList ← ''Validate''(G, S<sub>i-1</sub>, u)}}<br>
-{{pad|1em}}{{math|n<sub>i</sub> ← ''Min''({{!}}ValList{{!}}, Remainder)}}<br>
-{{pad|1em}}'''for''' {{math|k<sub>i</sub> {{=}} 1}} '''to''' {{math|n<sub>i</sub>}} '''do'''<br>
-{{pad|2em}}{{math|C ← ''Initial_Comb''(ValList, k<sub>i</sub>)}}<br>
-{{pad|2em}}(Make the first vertex combination selection according)<br>
-{{pad|2em}}'''repeat'''<br>
-{{pad|3em}}{{math|S<sub>i</sub> ← C}}<br>
-{{pad|3em}}{{math|''Enumerate_Vertex''(G, u, S, Remainder-k<sub>i</sub>, i+1)}}<br>
-{{pad|3em}}{{math|''Next_Comb''(ValList, k<sub>i</sub>)}}<br>
-{{pad|3em}}(Make the next vertex combination selection according)<br>
-{{pad|2em}}'''until''' {{math|C {{=}} NILL}}<br>
-{{pad|2em}}'''end for'''<br>
-{{pad|1em}}'''for each''' {{math|v ∈ ValList}} '''do'''<br>
-{{pad|2em}}{{math|Visited[v] ← false}}<br>
-{{pad|1em}}'''end for'''<br>
-'''end if'''
-|-
-|'''''Validate(G, Parents, u)'''''<br>
-'''Input:''' {{math|G}}: input graph, {{math|Parents}}: selected vertices of last layer, {{math|u}}: Root vertex.<br>
-'''Output:''' Valid vertices of the current level.
-{{math|ValList ← NILL}}<br>
-'''for each''' {{math|v ∈ Parents}} '''do'''<br>
-{{pad|1em}}'''for each''' {{math|w ∈ Neighbor[u]}} '''do'''<br>
-{{pad|2em}}'''if''' {{math|label[u] < label[w]}} '''AND NOT''' {{math|Visited[w]}} '''then'''<br>
-{{pad|3em}}{{math|Visited[w] ← true}}<br>
-{{pad|3em}}{{math|ValList {{=}} ValList + w}}<br>
-{{pad|2em}}'''end if'''<br>
-{{pad|1em}}'''end for'''<br>
-'''end for'''<br>
-'''return''' {{math|ValList}}<br>
-|}
-Recently a ''Cytoscape'' plugin called ''CytoKavosh'' <ref name="mas2">{{cite journal|author1=Ali Masoudi-Nejad |author2=Mitra Anasariola |author3=Ali Salehzadeh-Yazdi |author4=Sahand Khakabimamaghani |title=CytoKavosh: a Cytoscape Plug-in for Finding Network Motifs in Large Biological Networks |journal=PLoS ONE |volume=7 |issue=8 |pages=e43287 |year=2012 |doi=10.1371/journal.pone.0043287|pmid=22952659 |pmc=3430699 |bibcode=2012PLoSO...743287M }} {{open access}}</ref> is developed for this software. It is available via ''Cytoscape'' web page [http://apps.cytoscape.org/apps/cytokavosh].