使用pythony实现遗传算法
理论
遗传算法(Genetic Algorithms)是一种很有趣的理论,由密歇根大学的约翰·霍兰德(John Holland)和他的同事于二十世纪六十年代在对元胞自动机(cellular automata)研究时提出。在八十年代前,对于遗传算法的研究还仅仅限于理论方面,直到在匹兹堡召开了第一届世界遗传算法大会。随着计算机计算能力的发展和实际应用需求的增多,遗传算法逐渐进入实际应用阶段。
遗传算法的基本思想,是让程序像生物那样在交配,变异中进化,产生出更适宜环境的(逼近目标函数的)程序。
应用场景
遗传算法有很多不同的实现形式,一般都是用一个01串表达一个程序,但《集体智慧编程》(programming collective intelligence)里介绍了一种非常有意思的应用:用来寻找数据拟合的最优方程。
假如我们有如下数据:
许多人的第一直觉是使用多元回归来拟合方程f(x,y),但我们这里要用遗传算法来做这件事。我们打算用一个程序代表一个方程,然后让方程之间交配、变异,最终进化出一个最符合数据的方程。
技术难点及解决方案
--Ricky(讨论)这一部分讲到的案例属于遗传编程,即用遗传算法的原理获得一个计算机程序。个人认为是一种相当高级的应用,不利于入门级读者了解遗传算法。
使用树结构表达方程
要用程序表达方程,显然不可能直接用01串实现,因为任意构造的01串及其交配变异是没有数学意义的。我们要用解析树(parse tree)的概念
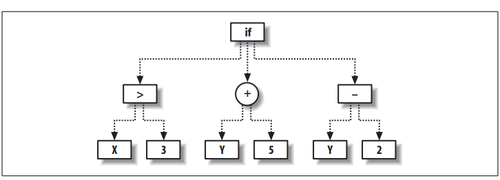
树上的每个节点或者表达一种对它子节点进行的数学操作,或者表达一个参数或变量。运算时,树从下往上收缩。
上述树就可以表达如下程序:
def func(x,y)
if x>3:
return y + 5
else:
return y - 2
因此,也就表达了一个方程。实际上,大多数程序语言在使用机器编译(compile)或解释(interpret)的时候,都是先变成这样一棵树。也许只有Lisp是例外,因为它相当于要求程序员直接写出这样的树结构。看起来树似乎只能表达比较简单的运算,但如果考虑到节点位置上的数学操作可以很复杂,例如欧式距离或者高斯函数,并且叶节点可以引用根节点,构成loop,树将可以表达非常复杂的运算。
变异(mutation)
变异对于01串表达程序的遗传算法模型来说就是随机地把一些0变成1或者相反。但在树结构里,我们定义两种变异:
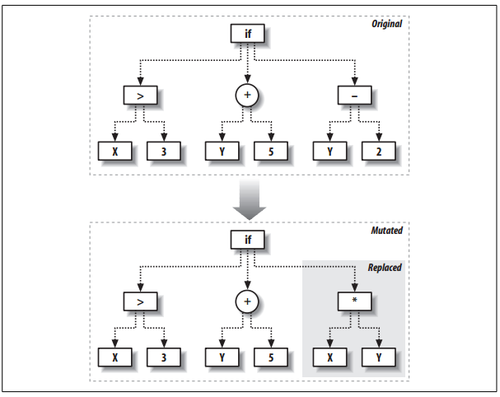
一种是改变节点上的操作符号:
一种是替换树的一部分枝干
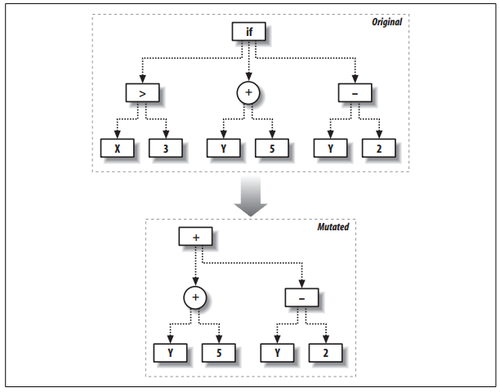
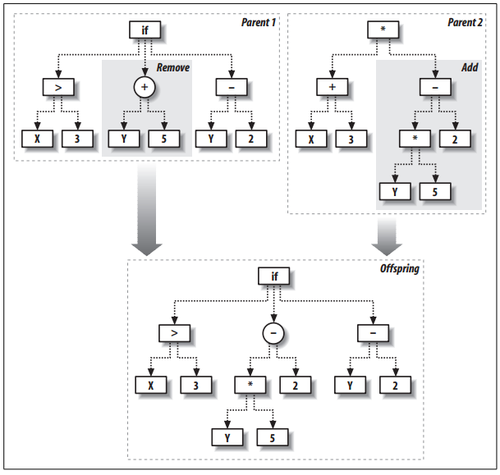
交配(crossover)
交配就是让两棵树相遇,互换一部分枝干,拼接出一棵新的树
python实现
我们先定义树的基本结构
from random import random,randint,choice
from copy import deepcopy
import numpy as np
class fwrapper:
def __init__(self,function,childcount,name):
self.function=function
self.childcount=childcount
self.name=name
class node:
def __init__(self,fw,children):
self.function=fw.function
self.name=fw.name
self.children=children
def evaluate(self,inp):
results=[n.evaluate(inp) for n in self.children]
return self.function(results)
def display(self,indent=0):
print (' '*indent)+self.name
for c in self.children:
c.display(indent+1)
class paramnode:
def __init__(self,idx):
self.idx=idx
def evaluate(self,inp):
return inp[self.idx]
def display(self,indent=0):
print '%sp%d' % (' '*indent,self.idx)
class constnode:
def __init__(self,v):
self.v=v
def evaluate(self,inp):
return self.v
def display(self,indent=0):
print '%s%d' % (' '*indent,self.v)
其中fwrapper代表着一种运算,它接受三个参数:函数的定义,函数里参数的个数,函数的名字。node就是一个节点,它的evaluate函数可以接受子节点的输入,并把fawapper定义的函数运用在子节点上,得到输出结果。它的display函数可以打印出节点以下的树的形式,方便我们分析程序内部表达的函数。paramnode是参数节点,总是返回输入的参数idx,constnode是常数节点,不管输入时什么,总是返回一个常数。
接下来我们定义一些基本的运算:
addw=fwrapper(lambda l:l[0]+l[1],2,'add')
subw=fwrapper(lambda l:l[0]-l[1],2,'subtract')
mulw=fwrapper(lambda l:l[0]*l[1],2,'multiply')
def iffunc(l):
if l[0]>0: return l[1]
else: return l[2]
ifw=fwrapper(iffunc,3,'if')
def isgreater(l):
if l[0]>l[1]: return 1
else: return 0
gtw=fwrapper(isgreater,2,'isgreater')
flist=[addw,mulw,ifw,gtw,subw]
其中加减乘都可以使用lambda一句话实现,但分段函数和比较函数要先定义一个函数,然后再用fwrapper。在flist里我们把这些函数都装起来,以便将来使用。
有了这些函数,其实我们已经可以定义一个示例树并观察其运算后果了
def exampletree( ):
return node(ifw,[
node(gtw,[paramnode(0),constnode(3)]),
node(addw,[paramnode(1),constnode(5)]),
node(subw,[paramnode(1),constnode(2)]),
]
)
exampletree=exampletree( )
exampletree.evaluate([2,3])
exampletree.evaluate([5,3])
exampletree.display( )
我们还可以制造随机树,用来作为演化的初始值
def makerandomtree(pc,maxdepth=4,fpr=0.5,ppr=0.6):
if random( )<fpr and maxdepth>0:
f=choice(flist)
children=[makerandomtree(pc,maxdepth-1,fpr,ppr)
for i in range(f.childcount)]
return node(f,children)
elif random( )<ppr:
return paramnode(randint(0,pc-1))
else:
return constnode(randint(0,10))
random1=makerandomtree(2)
random1.evaluate([7,1])
random1.evaluate([2,4])
random2=makerandomtree(2)
random2.evaluate([5,3])
random2.evaluate([5,20])
random1.display( )
random2.display( )
接下来我们定义变异和交配函数来对树结构进行操作。
def mutate(t,pc,probchange=0.1):
if random( )<probchange:
return makerandomtree(pc)
else:
result=deepcopy(t)
if isinstance(t,node):
result.children=[mutate(c,pc,probchange) for c in t.children]
return result
def crossover(t1,t2,probswap=0.7,top=1):
if random( )<probswap and not top:
return deepcopy(t2)
else:
result=deepcopy(t1)
if isinstance(t1,node) and isinstance(t2,node):
result.children=[crossover(c,choice(t2.children),probswap,0) for c in t1.children]
return result
random2.display( )
muttree=mutate(random2,2)
muttree.display( )
cross=crossover(random1,random2)
cross.display( )
为了准备测试数据,我们使用事先给定的函数制造一个数据。其实上面那张表里面的数据就是这么制造出来的。为了便于评估数据,我们还需要准备相应的衡量一棵树拟合数据的结果的函数。
def hiddenfunction(x,y):
return x**2+2*y+3*x+5
def buildhiddenset( ):
rows=[]
for i in range(200):
x=randint(0,10)
y=randint(0,10)
rows.append([x,y,hiddenfunction(x,y)])
return rows
def scorefunction(tree,s):
dif=0
for data in s:
v=tree.evaluate([data[0],data[1]])
dif+=abs(v-data[2])
return dif
def getrankfunction(dataset):
def rankfunction(population):
scores=[(scorefunction(t,dataset),t) for t in population]
scores.sort( )
return scores
return rankfunction
hiddenset=buildhiddenset( )
scorefunction(random2,hiddenset)
scorefunction(random1,hiddenset)
一切都准备好,就可以开始进行遗传算法的迭代了:
def evolve(pc,popsize,rankfunction,maxgen=500,
mutationrate=0.1,breedingrate=0.4,pexp=0.7,pnew=0.05):
# Returns a random number, tending towards lower numbers. The lower pexp
# is, more lower numbers you will get
def selectindex( ):
return int(np.log(random( ))/np.log(pexp))
# Create a random initial population
population=[makerandomtree(pc) for i in range(popsize)]
for i in range(maxgen):
scores=rankfunction(population)
print scores[0][0]
if scores[0][0]==0: break
# The two best always make it
newpop=[scores[0][1],scores[1][1]]
# Build the next generation
while len(newpop)<popsize:
if random( )>pnew:
newpop.append(mutate(
crossover(scores[selectindex( )][1],
scores[selectindex( )][1],
probswap=breedingrate),
pc,probchange=mutationrate))
else:
# Add a random node to mix things up
newpop.append(makerandomtree(pc))
population=newpop
scores[0][1].display( )
return scores[0][1]
rf=getrankfunction(buildhiddenset( ))
final = evolve(2,500,rf,mutationrate=0.2,breedingrate=0.1,pexp=0.7,pnew=0.1)
有趣的是,许多时候我们会找到和原始公式一模一样,但比原始公式复杂的树。其实对树本身的变换,也就是符号计算背后的原理。这样,我们就更理解为什么说数学系统其实也是一个图灵机了。