贝叶斯网络

此词条暂由水流心不竞初译，未经审校，带来阅读不便，请见谅。

A Bayesian network, Bayes network, belief network, decision network, Bayes(ian) model or probabilistic directed acyclic graphical model is a probabilistic graphical model (a type of statistical model) that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

A Bayesian network, Bayes network, belief network, decision network, Bayes(ian) model or probabilistic directed acyclic graphical model is a probabilistic graphical model (a type of statistical model) that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

贝叶斯网络、信念网络belief network、决策网络decision network、贝叶斯模型Bayes(ian) modelBayesian network或概率有向无环图模型probabilistic directed acyclic graphical modelBayesian network是一种概率图模型(一种统计模型) ，它通过有向无环图无环图(DAG)表示一组随机变量及其条件依赖关系。贝叶斯网络是一种理想的分析工具，用来预测一个事件的发生是由已知原因中的哪一个（些）引起的。例如，贝叶斯网络可以表示疾病和症状之间的概率关系。在给定症状的情况下，该网络可用于计算各种疾病出现的概率。

Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (e.g. speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams.

Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (e.g. speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams.

贝叶斯网络有多种变体。用来建模序列变量(例如，语音信号或蛋白质序列)的贝叶斯网络被称为动态贝叶斯网络。贝叶斯网络可以进一步扩展，用来表示和解决在不确定性因素下的决策问题，这种扩展称为影响图。现在已有高效的算法学习出贝叶斯网络的结构，并通过贝叶斯网络做推理。

图模型

Formally, Bayesian networks are directed acyclic graphs (DAGs) whose nodes represent variables in the Bayesian sense: they may be observable quantities, latent variables, unknown parameters or hypotheses. Edges represent conditional dependencies; nodes that are not connected (no path connects one node to another) represent variables that are conditionally independent of each other. Each node is associated with a probability function that takes, as input, a particular set of values for the node's parent variables, and gives (as output) the probability (or probability distribution, if applicable) of the variable represented by the node. For example, if [math]\displaystyle{ m }[/math] parent nodes represent [math]\displaystyle{ m }[/math] Boolean variables, then the probability function could be represented by a table of [math]\displaystyle{ 2^m }[/math] entries, one entry for each of the [math]\displaystyle{ 2^m }[/math] possible parent combinations. Similar ideas may be applied to undirected, and possibly cyclic, graphs such as Markov networks.

Formally, Bayesian networks are directed acyclic graphs (DAGs) whose nodes represent variables in the Bayesian sense: they may be observable quantities, latent variables, unknown parameters or hypotheses. Edges represent conditional dependencies; nodes that are not connected (no path connects one node to another) represent variables that are conditionally independent of each other. Each node is associated with a probability function that takes, as input, a particular set of values for the node's parent variables, and gives (as output) the probability (or probability distribution, if applicable) of the variable represented by the node. For example, if [math]\displaystyle{ m }[/math] parent nodes represent [math]\displaystyle{ m }[/math] Boolean variables, then the probability function could be represented by a table of [math]\displaystyle{ 2^m }[/math] entries, one entry for each of the [math]\displaystyle{ 2^m }[/math] possible parent combinations. Similar ideas may be applied to undirected, and possibly cyclic, graphs such as Markov networks.

在形式上，贝叶斯网络是有向无环图(DAG) ，其节点表示随机变量(其概率为贝叶斯概率): 它们可以是可观测量变量、隐变量、未知参数或假设。图中的边表示条件依赖; 未连接(没有路径连接一个节点到另一个节点)的节点表示彼此之间条件独立。每个节点都与一个 概率函数Probability function 节点相关联，该函数把所有父节点代表的变量值作为输入，并给出该节点表示的随机变量的概率(或概率分布话)。例如，如果 [math]\displaystyle{ m }[/math] 父节点表示 [math]\displaystyle{ m }[/math] 布尔变量，那么概率函数可以用一个包含[math]\displaystyle{ 2^m }[/math]行的表格表示，每一行代表一种（父节点）变量值的组合，以及对应的子节点变量的概率值。类似的想法可以应用于有环无向图，如马尔可夫网络。

举例

一个简单的贝叶斯网络，及其条件概率表

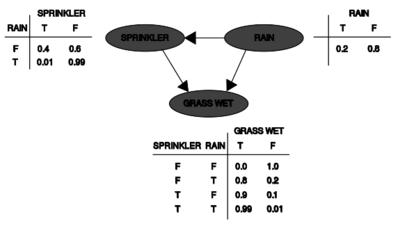
Two events can cause grass to be wet: an active sprinkler or rain. Rain has a direct effect on the use of the sprinkler (namely that when it rains, the sprinkler usually is not active). This situation can be modeled with a Bayesian network (shown to the right). Each variable has two possible values, T (for true) and F (for false).

Two events can cause grass to be wet: an active sprinkler or rain. Rain has a direct effect on the use of the sprinkler (namely that when it rains, the sprinkler usually is not active). This situation can be modeled with a Bayesian network (shown to the right). Each variable has two possible values, T (for true) and F (for false).

草地变得湿润，可能有两种原因: 主动洒水或者下雨。雨对洒水车的使用有直接的影响(也就是说，当下雨时，洒水车通常是不工作的)。这种情况可以用贝叶斯网络来模拟(如右图所示)。每个变量有两个可能的值，t (表示真)和 f (表示假)。

The joint probability function is:

The joint probability function is:

对应的联合概率函数是:

[math]\displaystyle{ \Pr(G,S,R)=\Pr(G\mid S,R) \Pr(S\mid R)\Pr(R) }[/math]

where G = "Grass wet (true/false)", S = "Sprinkler turned on (true/false)", and R = "Raining (true/false)".

where G = "Grass wet (true/false)", S = "Sprinkler turned on (true/false)", and R = "Raining (true/false)".

其中G表示“草地湿了(true/false)”，S表示“洒水器打开(true/false)”，R表示“下雨(true/false)”。

The model can answer questions about the presence of a cause given the presence of an effect (so-called inverse probability) like "What is the probability that it is raining, given the grass is wet?" by using the conditional probability formula and summing over all nuisance variables:

The model can answer questions about the presence of a cause given the presence of an effect (so-called inverse probability) like "What is the probability that it is raining, given the grass is wet?" by using the conditional probability formula and summing over all nuisance variables:

这个模型可以回答在给定一个结果的情况下一个原因是否存在的问题，比如“给定草是湿的，下雨的概率是多少? ”通过使用条件概率公式并对所有干扰变量的求和:

[math]\displaystyle{ \Pr(R=T\mid G=T) =\frac{\Pr(G=T,R=T)}{\Pr(G=T)} = \frac{\sum_{S \in \{T, F\}}\Pr(G=T, S,R=T)}{\sum_{S, R \in \{T, F\}} \Pr(G=T,S,R)} }[/math]

Using the expansion for the joint probability function [math]\displaystyle{ \Pr(G,S,R) }[/math] and the conditional probabilities from the conditional probability tables (CPTs) stated in the diagram, one can evaluate each term in the sums in the numerator and denominator. For example,

Using the expansion for the joint probability function [math]\displaystyle{ \Pr(G,S,R) }[/math] and the conditional probabilities from the conditional probability tables (CPTs) stated in the diagram, one can evaluate each term in the sums in the numerator and denominator. For example,

展开概率函数[math]\displaystyle{ \Pr(G,S,R) }[/math] ，并使用图中列出条件概率，我们可以算出分子和分母中的各个项。比如说,

[math]\displaystyle{ \begin{align} \Pr(G=T, S=T,R=T) & = \Pr(G=T\mid S=T,R=T)\Pr(S=T\mid R=T)\Pr(R=T) \\ & = 0.99 \times 0.01 \times 0.2 \\ & = 0.00198. \end{align} }[/math]

Then the numerical results (subscripted by the associated variable values) are

Then the numerical results (subscripted by the associated variable values) are

算出来的结果是

[math]\displaystyle{ \Pr(R=T\mid G=T) = \frac{ 0.00198_{TTT} + 0.1584_{TFT} }{ 0.00198_{TTT} + 0.288_{TTF} + 0.1584_{TFT} + 0.0_{TFF} } = \frac{891}{2491}\approx 35.77 \%. }[/math]

To answer an interventional question, such as "What is the probability that it would rain, given that we wet the grass?" the answer is governed by the post-intervention joint distribution function

To answer an interventional question, such as "What is the probability that it would rain, given that we wet the grass?" the answer is governed by the post-intervention joint distribution function

这个模型还回答干预性的问题，比如“现在我们把草弄湿了，那么下雨的可能性有多大? ”答案取决于干预后的联合分布函数：

[math]\displaystyle{ \Pr(S,R\mid\text{do}(G=T)) = \Pr(S\mid R) \Pr(R) }[/math]

obtained by removing the factor [math]\displaystyle{ \Pr(G\mid S,R) }[/math] from the pre-intervention distribution. The do operator forces the value of G to be true. The probability of rain is unaffected by the action:

obtained by removing the factor [math]\displaystyle{ \Pr(G\mid S,R) }[/math] from the pre-intervention distribution. The do operator forces the value of G to be true. The probability of rain is unaffected by the action:

该分布通过从干预前的分布中去除因子[math]\displaystyle{ \Pr(G\mid S,R) }[/math]得到，其中do算子强行使 G 的值为真。演算后可知下雨的可能性不受此干预的影响:

[math]\displaystyle{ \Pr(R\mid\text{do}(G=T)) = \Pr(R). }[/math]

To predict the impact of turning the sprinkler on:

To predict the impact of turning the sprinkler on:

现在再预测开启洒水装置的影响:

[math]\displaystyle{ \Pr(R,G\mid\text{do}(S=T)) = \Pr(R)\Pr(G\mid R,S=T) }[/math]

with the term [math]\displaystyle{ \Pr(S=T\mid R) }[/math] removed, showing that the action affects the grass but not the rain.

with the term [math]\displaystyle{ \Pr(S=T\mid R) }[/math] removed, showing that the action affects the grass but not the rain.

移除[math]\displaystyle{ \Pr(S=T\mid R) }[/math] 这个项表明这种行为影响的是草，而不是雨。

These predictions may not be feasible given unobserved variables, as in most policy evaluation problems. The effect of the action [math]\displaystyle{ \text{do}(x) }[/math] can still be predicted, however, whenever the back-door criterion is satisfied. It states that, if a set Z of nodes can be observed that d-separates (or blocks) all back-door paths from X to Y then

These predictions may not be feasible given unobserved variables, as in most policy evaluation problems. The effect of the action [math]\displaystyle{ \text{do}(x) }[/math] can still be predicted, however, whenever the back-door criterion is satisfied. It states that, if a set Z of nodes can be observed that d-separates (or blocks) all back-door paths from X to Y then

考虑到未观测变量，这些预测可能并不可行，就像大多数策略评估问题一样。但是，只要满足后门准则，仍然可以预测 [math]\displaystyle{ \text{do}(x) }[/math]的效果。如果一组观察到的变量Z能d-分隔(或阻塞)从 X 到 Y 的所有后门路径，则有

[math]\displaystyle{ \Pr(Y,Z\mid\text{do}(x)) = \frac{\Pr(Y,Z,X=x)}{\Pr(X=x\mid Z)}. }[/math]

A back-door path is one that ends with an arrow into X. Sets that satisfy the back-door criterion are called "sufficient" or "admissible." For example, the set Z = R is admissible for predicting the effect of S = T on G, because R d-separates the (only) back-door path S ← R → G. However, if S is not observed, no other set d-separates this path and the effect of turning the sprinkler on (S = T) on the grass (G) cannot be predicted from passive observations. In that case P(G | do(S = T)) is not "identified". This reflects the fact that, lacking interventional data, the observed dependence between S and G is due to a causal connection or is spurious

A back-door path is one that ends with an arrow into X. Sets that satisfy the back-door criterion are called "sufficient" or "admissible." For example, the set Z = R is admissible for predicting the effect of S = T on G, because R d-separates the (only) back-door path S ← R → G. However, if S is not observed, no other set d-separates this path and the effect of turning the sprinkler on (S = T) on the grass (G) cannot be predicted from passive observations. In that case P(G | do(S = T)) is not "identified". This reflects the fact that, lacking interventional data, the observed dependence between S and G is due to a causal connection or is spurious

后门路径是一条箭头指向X的路径。满足后门标准的（观测变量）集合称为“充分的”或“有效的”。例如，集合 Z = R 能有效地预测 S = T 对 G 的影响，因为 R d-分隔了(仅有的)后门路径 S ← R → G。但是，如果 S 没有被观测到，没有其他观测变量集合来 d-分隔这条路径，那就不能从观测数据中预测到“喷头被打开”(S = T)对于草地G的影响。在这种情况下，P(G | do(S = T))就没有被“识别”。这反映了一个事实：在缺乏干预性数据的情况下无法确认观察到的 S 和 G 之间的依赖关系是不是一种因果关系(可能由共同原因引起的强相关，比如辛普森悖论)。

(apparent dependence arising from a common cause, R). (see Simpson's paradox)

(apparent dependence arising from a common cause, R). (see Simpson's paradox)

(由共同原因引起的明显依赖关系，r)。(见辛普森悖论)

To determine whether a causal relation is identified from an arbitrary Bayesian network with unobserved variables, one can use the three rules of "do-calculus" and test whether all do terms can be removed from the expression of that relation, thus confirming that the desired quantity is estimable from frequency data.

To determine whether a causal relation is identified from an arbitrary Bayesian network with unobserved variables, one can use the three rules of "do-calculus" and test whether all do terms can be removed from the expression of that relation, thus confirming that the desired quantity is estimable from frequency data.

为了确定一个因果关系是否可以从一个含有未观测变量的贝叶斯网络中识别出来，我们可以使用“ do-演算”的三个规则来检验是否所有的 do 项都可以从这个关系的表达式中去掉，从而确认所需的量可以从数据中估计出来。

Using a Bayesian network can save considerable amounts of memory over exhaustive probability tables, if the dependencies in the joint distribution are sparse. For example, a naive way of storing the conditional probabilities of 10 two-valued variables as a table requires storage space for [math]\displaystyle{ 2^{10} = 1024 }[/math] values. If no variable's local distribution depends on more than three parent variables, the Bayesian network representation stores at most [math]\displaystyle{ 10\cdot2^3 = 80 }[/math] values.

Using a Bayesian network can save considerable amounts of memory over exhaustive probability tables, if the dependencies in the joint distribution are sparse. For example, a naive way of storing the conditional probabilities of 10 two-valued variables as a table requires storage space for [math]\displaystyle{ 2^{10} = 1024 }[/math] values. If no variable's local distribution depends on more than three parent variables, the Bayesian network representation stores at most [math]\displaystyle{ 10\cdot2^3 = 80 }[/math] values.

如果依赖关系在联合分布中是稀疏的（变量间依赖较少，即对应的图模型里的边较少），那么相对于存储一张完整的概率表，使用贝叶斯网络可以节省相当多的内存。例如，将10个二值变量的条件概率存储为一个表的，需要存储[math]\displaystyle{ 2^{10} = 1024 }[/math] 个值。而在每个变量最多依赖3个父变量的情况下，使用贝叶斯网络表示最多只存储[math]\displaystyle{ 10\cdot2^3 = 80 }[/math]个值。

One advantage of Bayesian networks is that it is intuitively easier for a human to understand (a sparse set of) direct dependencies and local distributions than complete joint distributions.

One advantage of Bayesian networks is that it is intuitively easier for a human to understand (a sparse set of) direct dependencies and local distributions than complete joint distributions.

相比于完全版的联合概率分布，理解(一组稀疏的)直接的变量间依赖关系和局部的概率分布对于人类来说要更加直观易懂。这正是贝叶斯网络的一个优点。

Inference and learning推论与学习

Bayesian networks perform three main inference tasks:

Bayesian networks perform three main inference tasks:

贝叶斯网络的推理和学习主要包含三个任务:

推断未观测变量

Because a Bayesian network is a complete model for its variables and their relationships, it can be used to answer probabilistic queries about them. For example, the network can be used to update knowledge of the state of a subset of variables when other variables (the evidence variables) are observed. This process of computing the posterior distribution of variables given evidence is called probabilistic inference. The posterior gives a universal sufficient statistic for detection applications, when choosing values for the variable subset that minimize some expected loss function, for instance the probability of decision error. A Bayesian network can thus be considered a mechanism for automatically applying Bayes' theorem to complex problems.

Because a Bayesian network is a complete model for its variables and their relationships, it can be used to answer probabilistic queries about them. For example, the network can be used to update knowledge of the state of a subset of variables when other variables (the evidence variables) are observed. This process of computing the posterior distribution of variables given evidence is called probabilistic inference. The posterior gives a universal sufficient statistic for detection applications, when choosing values for the variable subset that minimize some expected loss function, for instance the probability of decision error. A Bayesian network can thus be considered a mechanism for automatically applying Bayes' theorem to complex problems.

因为贝叶斯网络是变量及其关系的完整模型，所以它可以用来回答关于变量的概率问题。例如，当网络中某些变量被观测到时，也就是其确切值已知的情况下，我们可以更新对网络中其他未观测变量的认知。这种给定一些证据，然后计算的变量的后验概率的过程被称为概率推理。有时我们需要为某些变量赋值的同时最小化期望损失，此时后验概率为一些检测应用，例如检测决策错误的概率，提供了一个通用且充分的统计量。因此，贝叶斯网络可以被看作是一种应用贝叶斯定理解决复杂问题的自动化机制。

The most common exact inference methods are: variable elimination, which eliminates (by integration or summation) the non-observed non-query variables one by one by distributing the sum over the product; clique tree propagation, which caches the computation so that many variables can be queried at one time and new evidence can be propagated quickly; and recursive conditioning and AND/OR search, which allow for a space–time tradeoff and match the efficiency of variable elimination when enough space is used. All of these methods have complexity that is exponential in the network's treewidth. The most common approximate inference algorithms are importance sampling, stochastic MCMC simulation, mini-bucket elimination, loopy belief propagation, generalized belief propagation and variational methods.

The most common exact inference methods are: variable elimination, which eliminates (by integration or summation) the non-observed non-query variables one by one by distributing the sum over the product; clique tree propagation, which caches the computation so that many variables can be queried at one time and new evidence can be propagated quickly; and recursive conditioning and AND/OR search, which allow for a space–time tradeoff and match the efficiency of variable elimination when enough space is used. All of these methods have complexity that is exponential in the network's treewidth. The most common approximate inference algorithms are importance sampling, stochastic MCMC simulation, mini-bucket elimination, loopy belief propagation, generalized belief propagation and variational methods.

最常用的精确推理方法有: 变量消除法，即通过积分或求和的方式将未观察到的非查询变量逐一消除; 团树传播算法，它将计算过程缓存，可以同时查询多个变量，并快速传播新的证据; 递归条件化 AND/OR 搜索法，它考虑了时间和空间取舍，并且在使用足够的空间时拥有与变量消除法相比拟的时间效率。所有这些方法的复杂度都随网络树宽的增长呈指数级上升。而最常见的近似推理算法有重要性抽样法、随机 MCMC 模拟法、小桶消去法、循环置信传播法、广义置信传播法和变分法。

参数学习

In order to fully specify the Bayesian network and thus fully represent the joint probability distribution, it is necessary to specify for each node X the probability distribution for X conditional upon X's parents. The distribution of X conditional upon its parents may have any form. It is common to work with discrete or Gaussian distributions since that simplifies calculations. Sometimes only constraints on a distribution are known; one can then use the principle of maximum entropy to determine a single distribution, the one with the greatest entropy given the constraints. (Analogously, in the specific context of a dynamic Bayesian network, the conditional distribution for the hidden state's temporal evolution is commonly specified to maximize the entropy rate of the implied stochastic process.)

In order to fully specify the Bayesian network and thus fully represent the joint probability distribution, it is necessary to specify for each node X the probability distribution for X conditional upon Xs parents. The distribution of X conditional upon its parents may have any form. It is common to work with discrete or Gaussian distributions since that simplifies calculations. Sometimes only constraints on a distribution are known; one can then use the principle of maximum entropy to determine a single distribution, the one with the greatest entropy given the constraints. (Analogously, in the specific context of a dynamic Bayesian network, the conditional distribution for the hidden state's temporal evolution is commonly specified to maximize the entropy rate of the implied stochastic process.)

为了获得一个完整的贝叶斯网络，从而获得一个完整的联合概率分布，需要详知道每个节点 X 的条件概率分布。X 的条件概率分布可以有各种各样的形式，最长见到、用到的分布是离散分布或高斯分布，因为计算简便。有时我们只知道一个分布应该符合哪些约束条件。此时可以使用最大熵原理来确定一个分布，即给定约束条件下熵最大的分布。类似地，在动态贝叶斯网络B的特定上下文中，隐变量的条件分布通常也被认为是能最大化其随机过程的熵率的那一个分布。

Often these conditional distributions include parameters that are unknown and must be estimated from data, e.g., via the maximum likelihood approach. Direct maximization of the likelihood (or of the posterior probability) is often complex given unobserved variables. A classical approach to this problem is the expectation-maximization algorithm, which alternates computing expected values of the unobserved variables conditional on observed data, with maximizing the complete likelihood (or posterior) assuming that previously computed expected values are correct. Under mild regularity conditions this process converges on maximum likelihood (or maximum posterior) values for parameters.

Often these conditional distributions include parameters that are unknown and must be estimated from data, e.g., via the maximum likelihood approach. Direct maximization of the likelihood (or of the posterior probability) is often complex given unobserved variables. A classical approach to this problem is the expectation-maximization algorithm, which alternates computing expected values of the unobserved variables conditional on observed data, with maximizing the complete likelihood (or posterior) assuming that previously computed expected values are correct. Under mild regularity conditions this process converges on maximum likelihood (or maximum posterior) values for parameters.

通常这些条件分布包括未知的参数，必须从数据中估计出来，例如，使用 最大似然估计。给定未观测的变量，直接进行最大化似然(或后验概率)往往是很复杂的。这个问题的一个经典解决方案是EM算法。它利用观测数据计算出未观测变量的期望值，并假设先前计算的期望值是正确的，然后最大化完全似然(或后验)，求期望和最大化两个步骤交替迭代进行。在某些条件下，这个过程能收敛于待估计参数的最大似然值(或最大后验值)。

A more fully Bayesian approach to parameters is to treat them as additional unobserved variables and to compute a full posterior distribution over all nodes conditional upon observed data, then to integrate out the parameters. This approach can be expensive and lead to large dimension models, making classical parameter-setting approaches more tractable.

A more fully Bayesian approach to parameters is to treat them as additional unobserved variables and to compute a full posterior distribution over all nodes conditional upon observed data, then to integrate out the parameters. This approach can be expensive and lead to large dimension models, making classical parameter-setting approaches more tractable.

一个更彻底的贝叶斯估计方法是将参数视为附加的未观测变量，并根据观测数据计算包含所有节点的完整后验概率分布，然后积分出参数。这种方法可能代价高昂，并得出一个大规模的模型，但能使经典的参数估计方法更易于处理。

结构学习

In the simplest case, a Bayesian network is specified by an expert and is then used to perform inference. In other applications the task of defining the network is too complex for humans. In this case the network structure and the parameters of the local distributions must be learned from data.

In the simplest case, a Bayesian network is specified by an expert and is then used to perform inference. In other applications the task of defining the network is too complex for humans. In this case the network structure and the parameters of the local distributions must be learned from data.

在最简单的情况下，一个贝叶斯网络可以有领域专家人工构建，然后用它来执行推理。在其他应用程序中，构建网络的任务对于人类来说过于复杂。这种情况就必须从数据中学习网络结构和各个变量的局部分布。

Automatically learning the graph structure of a Bayesian network (BN) is a challenge pursued within machine learning. The basic idea goes back to a recovery algorithm developed by Rebane and Pearl and rests on the distinction between the three possible patterns allowed in a 3-node DAG:

Automatically learning the graph structure of a Bayesian network (BN) is a challenge pursued within machine learning. The basic idea goes back to a recovery algorithm developed by Rebane and Pearl and rests on the distinction between the three possible patterns allowed in a 3-node DAG:

自动化学习出贝叶斯网络的图形结构是机器学习领域的一个挑战。其基本思想可以追溯到由 Rebane 和 Pearl 提出的恢复算法。该算法的基础是三节点有向无环图中的三种可能模式:

Junction patterns

Pattern	Model
Chain	[math]\displaystyle{ X \rightarrow Y \rightarrow Z }[/math]
Fork	[math]\displaystyle{ X \leftarrow Y \rightarrow Z }[/math]
Collider	[math]\displaystyle{ X \rightarrow Y \leftarrow Z }[/math]

The first 2 represent the same dependencies ([math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] are independent given [math]\displaystyle{ Y }[/math]) and are, therefore, indistinguishable. The collider, however, can be uniquely identified, since [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] are marginally independent and all other pairs are dependent. Thus, while the skeletons (the graphs stripped of arrows) of these three triplets are identical, the directionality of the arrows is partially identifiable. The same distinction applies when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] have common parents, except that one must first condition on those parents. Algorithms have been developed to systematically determine the skeleton of the underlying graph and, then, orient all arrows whose directionality is dictated by the conditional independences observed.

The first 2 represent the same dependencies ([math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] are independent given [math]\displaystyle{ Y }[/math]) and are, therefore, indistinguishable. The collider, however, can be uniquely identified, since [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] are marginally independent and all other pairs are dependent. Thus, while the skeletons (the graphs stripped of arrows) of these three triplets are identical, the directionality of the arrows is partially identifiable. The same distinction applies when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] have common parents, except that one must first condition on those parents. Algorithms have been developed to systematically determine the skeleton of the underlying graph and, then, orient all arrows whose directionality is dictated by the conditional independences observed.

前2个种模式表示的依赖关系是相同的(在给定[math]\displaystyle{ Y }[/math] 时，[math]\displaystyle{ X }[/math] 和[math]\displaystyle{ Z }[/math]是独立的) ，因此无法区分。然而，第三种模式确实可以被识别的，因为[math]\displaystyle{ X }[/math] 和[math]\displaystyle{ Z }[/math]是边际独立的，而其他所有变量对都是依赖的。因此，虽然这三个节点的连接方式和前两种模式相同，但这种模式中箭头的方向是部分可识别的。当[math]\displaystyle{ X }[/math] 和[math]\displaystyle{ Z }[/math]有着共同的父母时，这种不同也能被识别。这个算法已经发展到能系统地确定图的框架，然后由从数据中观察到的条件独立性确定所有箭头的方向。

An alternative method of structural learning uses optimization-based search. It requires a scoring function and a search strategy. A common scoring function is posterior probability of the structure given the training data, like the BIC or the BDeu. The time requirement of an exhaustive search returning a structure that maximizes the score is superexponential in the number of variables. A local search strategy makes incremental changes aimed at improving the score of the structure. A global search algorithm like Markov chain Monte Carlo can avoid getting trapped in local minima. Friedman et al. discuss using mutual information between variables and finding a structure that maximizes this. They do this by restricting the parent candidate set to k nodes and exhaustively searching therein.

An alternative method of structural learning uses optimization-based search. It requires a scoring function and a search strategy. A common scoring function is posterior probability of the structure given the training data, like the BIC or the BDeu. The time requirement of an exhaustive search returning a structure that maximizes the score is superexponential in the number of variables. A local search strategy makes incremental changes aimed at improving the score of the structure. A global search algorithm like Markov chain Monte Carlo can avoid getting trapped in local minima. Friedman et al. discuss using mutual information between variables and finding a structure that maximizes this. They do this by restricting the parent candidate set to k nodes and exhaustively searching therein.

另一种结构学习的方法是基于优化的搜索。它需要一个评分函数和一个搜索策略。一个常见的评分函数是给定训练数据的结构的后验概率，比如 BIC 或 BDeu。穷举搜索可以获得能最大化得分函数的结构，但其时间要求随变量数增长呈超指数增长。局部搜索策略则进行增量改变，一步步迭代式改进结构的得分。像马尔可夫链蒙特卡洛这样的全局搜索算法可以避免陷入局部最优。弗里德曼等人认为可以使用变量之间的互信息，并找到一个讷讷感最大化互信息的结构，方法是通过将候选的父选节点集限制为 k 个节点并在其中进行穷尽式搜索。

A particularly fast method for exact BN learning is to cast the problem as an optimization problem, and solve it using integer programming. Acyclicity constraints are added to the integer program (IP) during solving in the form of cutting planes. Such method can handle problems with up to 100 variables.

A particularly fast method for exact BN learning is to cast the problem as an optimization problem, and solve it using integer programming. Acyclicity constraints are added to the integer program (IP) during solving in the form of cutting planes. Such method can handle problems with up to 100 variables.

一个特别快速精确学习出贝叶斯网络的方法是把问题转化为一个最优化问题，并使用整数规划解决它。以切平面的形式求解整数规划问题时，在整数规划中加入了不规则性约束，这种方法可以处理多达100个变量的问题。

In order to deal with problems with thousands of variables, a different approach is necessary. One is to first sample one ordering, and then find the optimal BN structure with respect to that ordering. This implies working on the search space of the possible orderings, which is convenient as it is smaller than the space of network structures. Multiple orderings are then sampled and evaluated. This method has been proven to be the best available in literature when the number of variables is huge.

In order to deal with problems with thousands of variables, a different approach is necessary. One is to first sample one ordering, and then find the optimal BN structure with respect to that ordering. This implies working on the search space of the possible orderings, which is convenient as it is smaller than the space of network structures. Multiple orderings are then sampled and evaluated. This method has been proven to be the best available in literature when the number of variables is huge.

处理成千上万个变量的问题时，则要用到不同的方。一种方法是采样出一个节点的（拓扑）排序，然后根据这种排序找到最优的网络结构。这意味着搜索工作只需要在包含可能排序的空间中进行，这比整个网络结构的搜索空间小，因而更加方便。可以进行多次采样和评估，这种方法在现有文献中已被证明在变量数量巨大的情况下是最佳的。

Another method consists of focusing on the sub-class of decomposable models, for which the MLE have a closed form. It is then possible to discover a consistent structure for hundreds of variables.

Another method consists of focusing on the sub-class of decomposable models, for which the MLE have a closed form. It is then possible to discover a consistent structure for hundreds of variables.

另一种方法是将重点放在具有可分解模型的子类上，其最大似然估计具有封闭形式。这样就有可能为数百个变量发现一致的结构。

Learning Bayesian networks with bounded treewidth is necessary to allow exact, tractable inference, since the worst-case inference complexity is exponential in the treewidth k (under the exponential time hypothesis). Yet, as a global property of the graph, it considerably increases the difficulty of the learning process. In this context it is possible to use K-tree for effective learning.

Learning Bayesian networks with bounded treewidth is necessary to allow exact, tractable inference, since the worst-case inference complexity is exponential in the treewidth k (under the exponential time hypothesis). Yet, as a global property of the graph, it considerably increases the difficulty of the learning process. In this context it is possible to use K-tree for effective learning.

学习树宽有限的贝叶斯网络对于精确的，可追溯的推理是必要的，因为最坏情况下的推理复杂度也只是树宽 k 的指数级（在指数时间假设下）。然而，作为图表的全局属性，它大大增加了学习过程的难度。在这种情况下，可以使用 K 树进行有效的学习。

统计学简介

Main article: Bayesian statistics

Given data [math]\displaystyle{ x\,\! }[/math] and parameter [math]\displaystyle{ \theta }[/math], a simple Bayesian analysis starts with a prior probability (prior) [math]\displaystyle{ p(\theta) }[/math] and likelihood [math]\displaystyle{ p(x\mid\theta) }[/math] to compute a posterior probability [math]\displaystyle{ p(\theta\mid x) \propto p(x\mid\theta)p(\theta) }[/math].

Given data [math]\displaystyle{ x\,\! }[/math] and parameter [math]\displaystyle{ \theta }[/math], a simple Bayesian analysis starts with a prior probability (prior) [math]\displaystyle{ p(\theta) }[/math] and likelihood [math]\displaystyle{ p(x\mid\theta) }[/math] to compute a posterior probability [math]\displaystyle{ p(\theta\mid x) \propto p(x\mid\theta)p(\theta) }[/math].

给定观测数据[math]\displaystyle{ x\,\! }[/math] 和模型参数 [math]\displaystyle{ \theta }[/math]，一个简单的贝叶斯分析任务就是用已知的先验概率[math]\displaystyle{ p(\theta) }[/math]和似然 [math]\displaystyle{ p(x\mid\theta) }[/math]，计算出后验概率[math]\displaystyle{ p(\theta\mid x) \propto p(x\mid\theta)p(\theta) }[/math]。

Often the prior on [math]\displaystyle{ \theta }[/math] depends in turn on other parameters [math]\displaystyle{ \varphi }[/math] that are not mentioned in the likelihood. So, the prior [math]\displaystyle{ p(\theta) }[/math] must be replaced by a likelihood [math]\displaystyle{ p(\theta\mid \varphi) }[/math], and a prior [math]\displaystyle{ p(\varphi) }[/math] on the newly introduced parameters [math]\displaystyle{ \varphi }[/math] is required, resulting in a posterior probability

Often the prior on [math]\displaystyle{ \theta }[/math] depends in turn on other parameters [math]\displaystyle{ \varphi }[/math] that are not mentioned in the likelihood. So, the prior [math]\displaystyle{ p(\theta) }[/math] must be replaced by a likelihood [math]\displaystyle{ p(\theta\mid \varphi) }[/math], and a prior [math]\displaystyle{ p(\varphi) }[/math] on the newly introduced parameters [math]\displaystyle{ \varphi }[/math] is required, resulting in a posterior probability

通常，先验概率[math]\displaystyle{ \theta }[/math]又依赖于并没有在似然中出现的参数[math]\displaystyle{ \varphi }[/math]，因此，必须用似然[math]\displaystyle{ p(\theta\mid \varphi) }[/math]代替先验概率[math]\displaystyle{ p(\theta) }[/math]，且需要用到新引入的参数[math]\displaystyle{ \varphi }[/math]的先验概率[math]\displaystyle{ p(\varphi) }[/math]。如此一来，新的后验概率就变成了

[math]\displaystyle{ p(\theta,\varphi\mid x) \propto p(x\mid\theta)p(\theta\mid\varphi)p(\varphi). }[/math]

This is the simplest example of a hierarchical Bayes model.模板:Clarify

This is the simplest example of a hierarchical Bayes model.

这是 层次贝叶斯模型hierarchical Bayes model最简单的例子。

The process may be repeated; for example, the parameters [math]\displaystyle{ \varphi }[/math] may depend in turn on additional parameters [math]\displaystyle{ \psi\,\! }[/math], which require their own prior. Eventually the process must terminate, with priors that do not depend on unmentioned parameters.

The process may be repeated; for example, the parameters [math]\displaystyle{ \varphi }[/math] may depend in turn on additional parameters [math]\displaystyle{ \psi\,\! }[/math], which require their own prior. Eventually the process must terminate, with priors that do not depend on unmentioned parameters.

这个过程可能会一直重复。例如，参数[math]\displaystyle{ \varphi }[/math]可能依次依赖于其他参数 [math]\displaystyle{ \psi\,\! }[/math]，这就又需要[math]\displaystyle{ \psi\,\! }[/math]的先验概率。最终，这个层次化嵌套的过程必须终止，亦即某参数的先验概率不依赖于其他参数。

工业级案例

Given the measured quantities [math]\displaystyle{ x_1,\dots,x_n\,\! }[/math]each with normally distributed errors of known standard deviation [math]\displaystyle{ \sigma\,\! }[/math],

Given the measured quantities [math]\displaystyle{ x_1,\dots,x_n\,\! }[/math]each with normally distributed errors of known standard deviation [math]\displaystyle{ \sigma\,\! }[/math],

给定观测到的一组测量数据[math]\displaystyle{ x_1,\dots,x_n\,\! }[/math]，每个数据点的误差都服从标准差为[math]\displaystyle{ \sigma\,\! }[/math]的正态分布：

[math]\displaystyle{ x_i \sim N(\theta_i, \sigma^2) }[/math]

Suppose we are interested in estimating the [math]\displaystyle{ \theta_i }[/math]. An approach would be to estimate the [math]\displaystyle{ \theta_i }[/math] using a maximum likelihood approach; since the observations are independent, the likelihood factorizes and the maximum likelihood estimate is simply

Suppose we are interested in estimating the [math]\displaystyle{ \theta_i }[/math]. An approach would be to estimate the [math]\displaystyle{ \theta_i }[/math] using a maximum likelihood approach; since the observations are independent, the likelihood factorizes and the maximum likelihood estimate is simply

假设我们想要估计[math]\displaystyle{ \theta_i }[/math]，一种方法是使用最大似然法。由于每个观测值是独立的，似然分解和最大似然估计很简单：

[math]\displaystyle{ \theta_i = x_i. }[/math]

However, if the quantities are related, so that for example the individual [math]\displaystyle{ \theta_i }[/math]have themselves been drawn from an underlying distribution, then this relationship destroys the independence and suggests a more complex model, e.g.,

However, if the quantities are related, so that for example the individual [math]\displaystyle{ \theta_i }[/math]have themselves been drawn from an underlying distribution, then this relationship destroys the independence and suggests a more complex model, e.g.,

然而，如果每个数据点相关的，例如每个[math]\displaystyle{ \theta_i }[/math]本身就是从一个潜在的分布中采样出来的出来的，那么这就破坏了独立性，并意味着要用到一个更复杂的模型，例如:

[math]\displaystyle{ x_i \sim N(\theta_i,\sigma^2), }[/math]

[math]\displaystyle{ \theta_i\sim N(\varphi, \tau^2), }[/math]

with improper priors [math]\displaystyle{ \varphi\sim\text{flat} }[/math], [math]\displaystyle{ \tau\sim\text{flat} \in (0,\infty) }[/math]. When [math]\displaystyle{ n\ge 3 }[/math], this is an identified model (i.e. there exists a unique solution for the model's parameters), and the posterior distributions of the individual [math]\displaystyle{ \theta_i }[/math] will tend to move, or shrink away from the maximum likelihood estimates towards their common mean. This shrinkage is a typical behavior in hierarchical Bayes models.

with improper priors [math]\displaystyle{ \varphi\sim\text{flat} }[/math], [math]\displaystyle{ \tau\sim\text{flat} \in (0,\infty) }[/math]. When [math]\displaystyle{ n\ge 3 }[/math], this is an identified model (i.e. there exists a unique solution for the model's parameters), and the posterior distributions of the individual [math]\displaystyle{ \theta_i }[/math] will tend to move, or shrink away from the maximum likelihood estimates towards their common mean. This shrinkage is a typical behavior in hierarchical Bayes models.

其中[math]\displaystyle{ \varphi\sim\text{flat} }[/math], [math]\displaystyle{ \tau\sim\text{flat} \in (0,\infty) }[/math]是不准确的先验概率。这是一个确定的模型(即，模型参数存在唯一解)，且每个[math]\displaystyle{ \theta_i }[/math]的后验分布会在最大似然估计中被移除，或者说收缩，换成了他们的均值。这种收缩是层次贝叶斯模型中的典型处理方法。

先验概率的约束条件

Some care is needed when choosing priors in a hierarchical model, particularly on scale variables at higher levels of the hierarchy such as the variable [math]\displaystyle{ \tau\,\! }[/math] in the example. The usual priors such as the Jeffreys prior often do not work, because the posterior distribution will not be normalizable and estimates made by minimizing the expected loss will be inadmissible.

Some care is needed when choosing priors in a hierarchical model, particularly on scale variables at higher levels of the hierarchy such as the variable [math]\displaystyle{ \tau\,\! }[/math] in the example. The usual priors such as the Jeffreys prior often do not work, because the posterior distribution will not be normalizable and estimates made by minimizing the expected loss will be inadmissible.

在层次结构模型中选择先验分布时需要特别注意，尤其是身处高层次的变量，比如上述例子中的变量 [math]\displaystyle{ \tau\,\! }[/math] 。常用的的先验分布，例如 Jeffreys先验往往不起作用，因为后验概率不是正规化的，而最小化预期损失得出的估计通常也无效。

Definitions and concepts定义与概念

See also: Glossary of graph theory § Directed acyclic graphs

Several equivalent definitions of a Bayesian network have been offered. For the following, let G = (V,E) be a directed acyclic graph (DAG) and let X = (X_v), v ∈ V be a set of random variables indexed by V.

Several equivalent definitions of a Bayesian network have been offered. For the following, let G = (V,E) be a directed acyclic graph (DAG) and let X = (X_v), v ∈ V be a set of random variables indexed by V.

贝叶斯网络现在有好几个等价的定义，在下文的介绍中我们用到两个符号设 G = (V,E)是一个有向无环图(DAG)，再设X = (X_v)为一组随机变量。

因子分解定义

X is a Bayesian network with respect to G if its joint probability density function (with respect to a product measure) can be written as a product of the individual density functions, conditional on their parent variables:模板:Sfn

X is a Bayesian network with respect to G if its joint probability density function (with respect to a product measure) can be written as a product of the individual density functions, conditional on their parent variables:

若一组随机变量X的联合概率分布函数可以写成由几个单独的条件概率函数的乘积，则X是关于图G的贝叶斯网络:

[math]\displaystyle{ p (x) = \prod_{v \in V} p \left(x_v \,\big|\, x_{\operatorname{pa}(v)} \right) }[/math]

where pa(v) is the set of parents of v (i.e. those vertices pointing directly to v via a single edge).

where pa(v) is the set of parents of v (i.e. those vertices pointing directly to v via a single edge).

其中 pa(v)是 v 的父变量的集合(即，这些顶点通过一条边直接指向 v)。

For any set of random variables, the probability of any member of a joint distribution can be calculated from conditional probabilities using the chain rule (given a topological ordering of X) as follows:模板:Sfn

For any set of random variables, the probability of any member of a joint distribution can be calculated from conditional probabilities using the chain rule (given a topological ordering of X) as follows:

对于任何一组随机变量，他们各种取值组合的联合概率都可以通过使用链式规则(给定一个 X 的拓扑排序)从条件概率中计算出来，如下所示:

[math]\displaystyle{ \operatorname P(X_1=x_1, \ldots, X_n=x_n) = \prod_{v=1}^n \operatorname P \left(X_v=x_v \mid X_{v+1}=x_{v+1}, \ldots, X_n=x_n \right) }[/math]

Using the definition above, this can be written as:

Using the definition above, this can be written as:

使用上面贝叶斯网络的定义，还可以写成这样:

[math]\displaystyle{ \operatorname P(X_1=x_1, \ldots, X_n=x_n) = \prod_{v=1}^n \operatorname P (X_v=x_v \mid X_j=x_j \text{ for each } X_j\, \text{ that is a parent of } X_v\, ) }[/math]

The difference between the two expressions is the conditional independence of the variables from any of their non-descendants, given the values of their parent variables.

The difference between the two expressions is the conditional independence of the variables from any of their non-descendants, given the values of their parent variables.

这两个表达式之间的区别是：给定父变量值，所有变量与他们的非后代变量条件独立。

局部马尔可夫性

X is a Bayesian network with respect to G if it satisfies the local Markov property: each variable is conditionally independent of its non-descendants given its parent variables:模板:Sfn

X is a Bayesian network with respect to G if it satisfies the local Markov property: each variable is conditionally independent of its non-descendants given its parent variables:

若一组随机变量X满足局部马尔可夫性，即每个变量在给定父变量的情况下，条件独立于所有非后代变量，则称 X是关于 G 的一个贝叶斯网络: :

[math]\displaystyle{ X_v \perp\!\!\!\perp X_{V \,\smallsetminus\, \operatorname{de}(v)} \mid X_{\operatorname{pa}(v)} \quad\text{for all }v \in V }[/math]

where de(v) is the set of descendants and V \ de(v) is the set of non-descendants of v.

where de(v) is the set of descendants and V \ de(v) is the set of non-descendants of v.

其中 de(v)是节点v的后代集合，V \ de(v)是节点v的非后代集合。

This can be expressed in terms similar to the first definition, as

This can be expressed in terms similar to the first definition, as

这可以用类似于第一个定义的术语来表示，如

[math]\displaystyle{ \begin{align} & \operatorname P(X_v=x_v \mid X_i=x_i \text{ for each } X_i \text{ that is not a descendant of } X_v\, ) \\[6pt] = {} & P(X_v=x_v \mid X_j=x_j \text{ for each } X_j \text{ that is a parent of } X_v\, ) \end{align} }[/math]

The set of parents is a subset of the set of non-descendants because the graph is acyclic.

The set of parents is a subset of the set of non-descendants because the graph is acyclic.

因为贝叶斯网络是无环图，所以每个节点的父节点集同时也是该节点的是非后代节点集的一个子集。

生成一个贝叶斯网络

Developing a Bayesian network often begins with creating a DAG G such that X satisfies the local Markov property with respect to G. Sometimes this is a causal DAG. The conditional probability distributions of each variable given its parents in G are assessed. In many cases, in particular in the case where the variables are discrete, if the joint distribution of X is the product of these conditional distributions, then X is a Bayesian network with respect to G.

Developing a Bayesian network often begins with creating a DAG G such that X satisfies the local Markov property with respect to G. Sometimes this is a causal DAG. The conditional probability distributions of each variable given its parents in G are assessed. In many cases, in particular in the case where the variables are discrete, if the joint distribution of X is the product of these conditional distributions, then X is a Bayesian network with respect to G.

生成一个贝叶斯网络通常从创建一个有向无环图G开始，然后使图G里的随机变量X满足的局部马尔可夫性。有时这个图同时还是一个因果图。接下来，图里的每一个随机变量的概率分布都要被估计出来。在许多情况下，特别是在变量都是离散的情况下，如果 X 的联合分布是这些单个随机变量的条件分布的乘积，那么 X 就是 G 的贝叶斯网络。

马尔科夫毯

The Markov blanket of a node is the set of nodes consisting of its parents, its children, and any other parents of its children. The Markov blanket renders the node independent of the rest of the network; the joint distribution of the variables in the Markov blanket of a node is sufficient knowledge for calculating the distribution of the node. X is a Bayesian network with respect to G if every node is conditionally independent of all other nodes in the network, given its Markov blanket.模板:Sfn

The Markov blanket of a node is the set of nodes consisting of its parents, its children, and any other parents of its children. The Markov blanket renders the node independent of the rest of the network; the joint distribution of the variables in the Markov blanket of a node is sufficient knowledge for calculating the distribution of the node. X is a Bayesian network with respect to G if every node is conditionally independent of all other nodes in the network, given its Markov blanket.

一个节点的马尔可夫毯是由其父节点、其子节点和其子节点的所有其他父节点组成的节点集。一个节点的马尔可夫毯可以使该节点独立于网络的其余部分。一个节点的马尔可夫毯中所有变量的联合分布是计算该节点分布的一个充分条件。如果网络中的每个节点再给定其马尔可夫毯的情况下，条件地独立于网络中的所有其他节点，那么 X 就是 G 的贝叶斯网络。

d-分隔

This definition can be made more general by defining the "d"-separation of two nodes, where d stands for directional. We first define the "d"-separation of a trail and then we will define the "d"-separation of two nodes in terms of that.

This definition can be made more general by defining the "d"-separation of two nodes, where d stands for directional. We first define the "d"-separation of a trail and then we will define the "d"-separation of two nodes in terms of that.

使用d-分隔的概念，贝叶斯网络的定义可以更加通用，其中 d 代表有向(directed)。我们首先定义一条轨迹的d-分隔的线索，然后我们再定义两个节点间的d-分隔。

Let P be a trail from node u to v. A trail is a loop-free, undirected (i.e. all edge directions are ignored) path between two nodes. Then P is said to be d-separated by a set of nodes Z if any of the following conditions holds:

Let P be a trail from node u to v. A trail is a loop-free, undirected (i.e. all edge directions are ignored) path between two nodes. Then P is said to be d-separated by a set of nodes Z if any of the following conditions holds:

设 P 是从节点 u 到节点 v 的轨迹。轨迹是一条两个节点之间的无环、无向的(即所有边方向被忽略)的路径。如果下列任何一个条件成立，则称 P 被一组节点 Z 分隔:

• P contains (but does not need to be entirely) a directed chain, [math]\displaystyle{ u \cdots \leftarrow m \leftarrow \cdots v }[/math] or [math]\displaystyle{ u \cdots \rightarrow m \rightarrow \cdots v }[/math], such that the middle node m is in Z,
• “P”包含一条有向链[math]\displaystyle{ u \cdots \leftarrow m \leftarrow \cdots v }[/math] or [math]\displaystyle{ u \cdots \rightarrow m \rightarrow \cdots v }[/math], 其中间节点m属于点集Z，
• P contains a fork, [math]\displaystyle{ u \cdots \leftarrow m \rightarrow \cdots v }[/math], such that the middle node m is in Z, or
• “P”包含一个分叉[math]\displaystyle{ u \cdots \leftarrow m \rightarrow \cdots v }[/math], 其中间节点m位于“Z”中，或
• P contains an inverted fork (or collider), [math]\displaystyle{ u \cdots \rightarrow m \leftarrow \cdots v }[/math], such that the middle node m is not in Z and no descendant of m is in Z.
• “P”包含一个倒叉（或称对撞），[math]\displaystyle{ u \cdots \rightarrow m \leftarrow \cdots v }[/math]，其中间节点m不在Z中，在Z中也没有m的后代节点。

The nodes u and v are d-separated by Z if all trails between them are d-separated. If u and v are not d-separated, they are d-connected.

The nodes u and v are d-separated by Z if all trails between them are d-separated. If u and v are not d-separated, they are d-connected.

如果节点 u 和 v 之间的所有轨迹都是d-分隔的，则称节点 u 和 v 被 Z 分开。如果 'u 和 v 不是d-分隔的，则称它们是 ‘’d‘’-连通的。

X is a Bayesian network with respect to G if, for any two nodes u, v:

X is a Bayesian network with respect to G if, for any two nodes u, v:

我们称X是G的贝叶斯网络，当对于图G中任意两个节点 u，v满足:

[math]\displaystyle{ X_u \perp\!\!\!\perp X_v \mid X_Z }[/math]

where Z is a set which d-separates u and v. (The Markov blanket is the minimal set of nodes which d-separates node v from all other nodes.)

where Z is a set which d-separates u and v. (The Markov blanket is the minimal set of nodes which d-separates node v from all other nodes.)

其中 Z 是一个将 u 和 v进行了 d-分隔的集合(马尔可夫毯其实就是将节点 v 与其他所有节点d-分隔的最小节点集合)。

因果网络

Although Bayesian networks are often used to represent causal relationships, this need not be the case: a directed edge from u to v does not require that X_v be causally dependent on X_u. This is demonstrated by the fact that Bayesian networks on the graphs:

Although Bayesian networks are often used to represent causal relationships, this need not be the case: a directed edge from u to v does not require that X_v be causally dependent on X_u. This is demonstrated by the fact that Bayesian networks on the graphs:

虽然贝叶斯网络经常被用来表示因果关系，但这种情形并不是必须的: 从 u 到 v 的有向边并不意味着 X_v一定是X_u导致的结果。下面这两个贝叶斯网络是等价的:

[math]\displaystyle{ a \rightarrow b \rightarrow c \qquad \text{and} \qquad a \leftarrow b \leftarrow c }[/math]

are equivalent: that is they impose exactly the same conditional independence requirements.

are equivalent: that is they impose exactly the same conditional independence requirements.

也就是说，它们表示的条件独立要求完全相同。

A causal network is a Bayesian network with the requirement that the relationships be causal. The additional semantics of causal networks specify that if a node X is actively caused to be in a given state x (an action written as do(X = x)), then the probability density function changes to that of the network obtained by cutting the links from the parents of X to X, and setting X to the caused value x. Using these semantics, the impact of external interventions from data obtained prior to intervention can be predicted.

A causal network is a Bayesian network with the requirement that the relationships be causal. The additional semantics of causal networks specify that if a node X is actively caused to be in a given state x (an action written as do(X = x)), then the probability density function changes to that of the network obtained by cutting the links from the parents of X to X, and setting X to the caused value x. Using these semantics, the impact of external interventions from data obtained prior to intervention can be predicted.

当一个贝叶斯网络中的节点关系全都是因果关系时，这网络才能被称为时因果网络。因果网络还规定，如果一个节点 X再被干预的情况下变成了状态 x (写作do(X = x)) ，那么概率密度函数就会发生改变，表示成一个从 X 的父节点到 X的链接被切断的网络，并将变量X的值设置为x。利用这些规则，我们可以在真正实施外部干预前，就能从数据中预测到实施干预后会产生的影响。

推理复杂度与近似算法

In 1990, while working at Stanford University on large bioinformatic applications, Cooper proved that exact inference in Bayesian networks is NP-hard. This result prompted research on approximation algorithms with the aim of developing a tractable approximation to probabilistic inference. In 1993, Dagum and Luby proved two surprising results on the complexity of approximation of probabilistic inference in Bayesian networks. First, they proved that no tractable deterministic algorithm can approximate probabilistic inference to within an absolute error ɛ < 1/2. Second, they proved that no tractable randomized algorithm can approximate probabilistic inference to within an absolute error ɛ < 1/2 with confidence probability greater than 1/2.

1990年，Cooper在斯坦福大学研究大规模生物信息学应用时，证明了贝叶斯网络中的精确推理是NP-hard（NP难问题，NP 是指非确定性多项式( non-deterministic polynomial ,缩写 NP ) 。 这个结果促进了近似算法的研究，目的是开发出一种易于处理的近似方法来进行概率推理。1993年，Dagum 和 Luby 证明了贝叶斯网络中近似概率推理复杂度的两个令人惊讶的结果。首先，他们证明了任何易于处理的确定性近似概率推断算法的绝对误差都不可能小于1/2。其次，他们证明了没有任何易于处理的随机化的近似概率推断算法可以在置信度大于1 / 2的情况下，误差小于1 / 2。

At about the same time, Roth proved that exact inference in Bayesian networks is in fact #P-complete (and thus as hard as counting the number of satisfying assignments of a conjunctive normal form formula (CNF) and that approximate inference within a factor 2^n1−ɛ for every ɛ > 0, even for Bayesian networks with restricted architecture, is NP-hard.

At about the same time, Roth proved that exact inference in Bayesian networks is in fact #P-complete (and thus as hard as counting the number of satisfying assignments of a conjunctive normal form formula (CNF) and that approximate inference within a factor 2^n1−ɛ for every ɛ > 0, even for Bayesian networks with restricted architecture, is NP-hard.

与此同时，Roth 证明了贝叶斯网络中的精确推理实际上是 #P-完全的(因此就像计数使得一个合取范式表达式(CNF)为真的赋值的数量一样困难) 。即使对于受限结构的贝叶斯网络来说，在对于任意ɛ > 0，2^n1−ɛ 的近似推理也是 NP-hard的。

In practical terms, these complexity results suggested that while Bayesian networks were rich representations for AI and machine learning applications, their use in large real-world applications would need to be tempered by either topological structural constraints, such as naïve Bayes networks, or by restrictions on the conditional probabilities. The bounded variance algorithm was the first provable fast approximation algorithm to efficiently approximate probabilistic inference in Bayesian networks with guarantees on the error approximation. This powerful algorithm required the minor restriction on the conditional probabilities of the Bayesian network to be bounded away from zero and one by 1/p(n) where p(n) was any polynomial on the number of nodes in the network n.

In practical terms, these complexity results suggested that while Bayesian networks were rich representations for AI and machine learning applications, their use in large real-world applications would need to be tempered by either topological structural constraints, such as naïve Bayes networks, or by restrictions on the conditional probabilities. The bounded variance algorithm was the first provable fast approximation algorithm to efficiently approximate probabilistic inference in Bayesian networks with guarantees on the error approximation. This powerful algorithm required the minor restriction on the conditional probabilities of the Bayesian network to be bounded away from zero and one by 1/p(n) where p(n) was any polynomial on the number of nodes in the network n.

实际上，这些复杂性结果表明，虽然贝叶斯网络在人工智能和机器学习应用中是一种强大的表示，但它们在大型实际应用中需要对拓扑结构施加约束(如朴素贝叶斯网络)或对条件概率施加约束。有界方差算法 Bounded variance algorithm 是贝叶斯网络中第一个被证明在保证误差的情况下还能进行快速近似概率推理的算法。这个强大的算法需要对贝叶斯网络的条件概率进行细微的限制，使其处于[0 + 1/p(n), 1 - 1/p(n)]的区间内 ，其中 p (n)是网络中节点数n的任意多项式。

Software软件

! ——这个列表中的条目与来源于维基百科的文章同样“值得注意”。参见 WP: GNG 和 WP: WTAF。-->

Notable software for Bayesian networks include:

Notable software for Bayesian networks include:

著名的贝叶斯网络软件包括:

• Just another Gibbs sampler (JAGS) – Open-source alternative to WinBUGS. Uses Gibbs sampling.
• Just another Gibbs sampler (JAGS) WinBUGS的开源替代品。使用吉布斯抽样法
• OpenBUGS – Open-source development of WinBUGS.
• OpenBUGS –WinBUGS的开源开发。
• SPSS Modeler – Commercial software that includes an implementation for Bayesian networks.
• SPSS Modeler –包括贝叶斯网络实现的商业软件。
• Stan (software) – Stan is an open-source package for obtaining Bayesian inference using the No-U-Turn sampler (NUTS), a variant of Hamiltonian Monte Carlo.
• Stan (software) – stan是一个开源软件包，用于使用不掉头取样器（NUTS），

|pages=329–334 |url=http://ftp.cs.ucla.edu/tech-report/198_-reports/850017.pdf%7Caccess-date=2009-05-01 |format=UCLA Technical Report CSD-850017}}</ref>

| 第329-334页 | 网址 / http://ftp.cs.UCLA.edu/tech-Report/198_-reports/850017.pdf%7Caccess-date=2009-05-01 / 格式 / UCLA 技术报告 / CSD-850017} / ref

• the often subjective nature of the input information
• 输入信息通常是主观的
• the reliance on Bayes' conditioning as the basis for updating information
• 依赖贝叶斯条件作为信息更新的基础
• the distinction between causal and evidential modes of reasoning
• 因果推理和证据推理模式的区别

In the late 1980s Pearl's Probabilistic Reasoning in Intelligent Systems and Neapolitan's Probabilistic Reasoning in Expert Systems summarized their properties and established them as a field of study.

In the late 1980s Pearl's Probabilistic Reasoning in Intelligent Systems and Neapolitan's Probabilistic Reasoning in Expert Systems summarized their properties and established them as a field of study.

20世纪80年代后期，皮尔的《智能系统中的概率推理》和那不勒斯的《专家系统中的概率推理》总结了它们的性质，并将它们确立为一个研究领域。

See also又及

{ columns-list

The unnamed parameter 2= is no longer supported. Please see the documentation for {{columns-list}}.

colwidth 30em

}}

Further reading 延伸阅读

• Conrady, Stefan; Jouffe, Lionel (2015-07-01). [[[:模板:Google books]] Bayesian Networks and BayesiaLab – A practical introduction for researchers]. Franklin, Tennessee: Bayesian USA. ISBN 978-0-9965333-0-0. 模板:Google books. 

• Charniak, Eugene (Winter 1991). "Bayesian networks without tears" (PDF). AI Magazine. {{cite web}}: Unknown parameter |name-list-format= ignored (help)

• Kruse, Rudolf; Borgelt, Christian; Klawonn, Frank; Moewes, Christian; Steinbrecher, Matthias; Held, Pascal (2013). [[[:模板:Google books]] Computational Intelligence A Methodological Introduction]. London: Springer-Verlag. ISBN 978-1-4471-5012-1. 模板:Google books. 

• Borgelt, Christian; Steinbrecher, Matthias; Kruse, Rudolf (2009). [[[:模板:Google books]] Graphical Models – Representations for Learning, Reasoning and Data Mining] (Second ed.). Chichester: Wiley. ISBN 978-0-470-74956-2. 模板:Google books. 

External links 外部链接

• An Introduction to Bayesian Networks and their Contemporary Applications

• On-line Tutorial on Bayesian nets and probability

• Web-App to create Bayesian nets and run it with a Monte Carlo method

• Continuous Time Bayesian Networks

• Bayesian Networks: Explanation and Analogy

• A live tutorial on learning Bayesian networks

• A hierarchical Bayes Model for handling sample heterogeneity in classification problems, provides a classification model taking into consideration the uncertainty associated with measuring replicate samples.

• Hierarchical Naive Bayes Model for handling sample uncertainty, shows how to perform classification and learning with continuous and discrete variables with replicated measurements.

Category:Graphical models

类别: 图形模型

Category:Causality

分类: 因果关系

Category:Causal inference

类别: 因果推理

This page was moved from wikipedia:en:Bayesian network. Its edit history can be viewed at 贝叶斯网络/edithistory