信息论

信息论 Information Theory研究的是信息的量化、存储与传播。信息论最初是由克劳德·香农 Claude Shannon在1948年的一篇题为《一种通信的数学理论(A Mathematical Theory of Communication)》的里程碑式论文中提出的，其目的是找到信号处理和通信操作（如数据压缩）的基本限制。信息论对于旅行者号深空探测任务的成功、光盘的发明、移动电话的可行性、互联网的发展、语言学和人类感知的研究、对黑洞的理解以及许多其他领域的研究都是至关重要的。

该领域是数学、统计学、计算机科学、物理学、神经生物学、信息工程和电气工程的交叉学科。这一理论也在其他领域得到了应用，比如推论统计学、自然语言处理、密码学、神经生物学、人类视觉、分子编码的进化、和功能（生物信息学）、统计学中的模型选择、热物理学 、量子计算、语言学、剽窃检测、模式识别和异常检测。

信息论的重要分支包括信源编码、算法复杂性理论、算法信息论、信息理论安全性、灰色系统理论和信息度量。

信息论在应用领域的基本课题包括无损数据压缩(例如:ZIP压缩文件)、有损数据压缩(例如:Mp3和jpeg格式) ，以及频道编码(例如:DSL)。信息论在信息检索、情报收集、赌博，甚至在音乐创作中也有应用。

信息论中的一个关键度量是熵。熵量化了一个随机变量的值或者一个随机过程的结果所包含的不确定性。例如，识别一次公平抛硬币的结果（有两个同样可能的结果）所提供的信息（较低的熵）少于识别抛一次骰子的结果（有六个同样可能的结果）。信息论中的其他一些重要指标有：互信息、信道容量、误差指数和相对熵。

概览

信息论主要研究信息的传递、处理、提取和利用。抽象地说，信息可以作为不确定性的解决方案。1948年，克劳德·香农在他的论文《一种通信的数学理论》中将这个抽象的概念具体化，在这篇论文中“信息”被认为是一组可能的信号，这些信号在通过带有噪声的信道发送后，接收者能在信道噪声的影响下以较低的错误概率来重构这些信号。香农的主要结论，有噪信道编码定理，表明在信道使用的许多限制情况下，渐近可达到信息传输速率等于的信道容量，一个仅仅依赖于信息发送所经过的信道本身的统计量。（译注：当信道的信息传输率不超过信道容量时，采用合适的编码方法可以实现任意高的传输可靠性，但若信息传输率超过了信道容量，就不可能实现可靠的传输。）

信息论与一系列纯科学和应用科学密切相关。在过去半个世纪甚至更久的时间里，在全球范围内已经有各种各样的学科理论被研究和化归为工程实践，比如在自适应系统，预期系统，人工智能，复杂系统，复杂性科学，控制论，信息学，机器学习，以及系统科学。信息论是一个广博而深遂的数学理论，也具有广泛而深入的应用，其中编码理论是至关重要的领域。

编码理论与寻找明确的方法（编码）有关，用于提高效率和将有噪信道上传输的数据错误率降低到接近信道容量。这些编码可大致分为数据压缩编码（信源编码）和纠错（信道编码）技术。对于纠错技术，香农证明了理论极限很多年后才有人找到了真正实现了理论最优的方法。

第三类信息论代码是密码算法（包括密文和密码）。编码理论和信息论的概念、方法和结果在密码学和密码分析中得到了广泛的应用。

历史背景

1948年7月和10月，克劳德·E·香农在《贝尔系统技术期刊》上发表了经典论文：《一种通信的数学理论》，这就是建立信息论学科并立即引起全世界关注的里程碑事件。

在此之前，贝尔实验室已经提出了有限的信息论思想，所有这些理论都隐性地假设了概率均等的事件。Harry Nyquist 在1924年发表的论文《集中影响电报速率的因素（Certain Factors Affecting Telegraph Speed）》中包含一个理论章节，量化了“情报”和通信系统可以传输的“线路速度”，并给出了关系式 W = K log m (参考玻尔兹曼常数) ，其中 W 是情报传输的速度， m 是每个时间步长可以选择的不同电压电平数，K 是常数。Ralph Hartley 在1928年发表的论文《信息的传输（ Transmission of Information）》中，将单词信息作为一个可测量的量，以此反映接收者区分一系列符号的能力，从而将信息量化为 H = log Sⁿ = n log S，其中 S 是可以使用的符号的数量，n 是传输中符号的数量。因此信息的单位就是十进制数字，为了表示对他的尊敬，这个单位有时被称为 Hartley，作为信息的单位、尺度或度量。1940年，图灵在二战时期破解德国的“迷”密码（Enigma ciphers）的统计分析中使用了类似的思想。

信息论背后的许多数学理论（包括不同概率的事件）都是由路德维希·玻尔兹曼和约西亚·威拉德·吉布斯为热力学领域开发出来的。

香农的那篇革命性的、开创性的论文，于1944年的年底便已基本在贝尔实验室完成。在这论文里，香农将通信看作一个统计学过程，首次提出了通信的量化模型，并以此为基础推导出了信息论。论文开篇便提出了一下论断：

“通信的基本问题是在一点上精确地或近似地再现在另一点上选择的信息”

与此相关的一些想法包括：

• 信息熵和信源冗余，以及信源编码定理；

• 互信息，有噪信道的信道容量，包括无损通信的证明，和有噪信道编码定理；

• 香农-哈特利定律 Shannon–Hartley law应用于高斯信道的信道容量的结果，以及

• 比特 bit——一种新的度量信息的最基本单位

信息的度量

信息论基于概率论和统计学，其中经常涉及衡量随机变量的分布的信息。信息论中重要的信息量有：熵（单个随机变量中信息的度量）和互信息（两个随机变量之间的信息的度量）。熵是随机变量的概率分布的一个属性，它限制了从给定分布中独立采样得到的数据的压缩率。互信息是两个随机变量的联合概率分布的一个属性，是当信道的统计量由联合分布确定时，在长块长度的限制下，通过有噪信道的可靠通信的最大速率。

在下列公式中，对数底数的选择决定了信息熵的单位。信息的常见单位是比特（基于二进制对数）。其他单位包括 nat（自然对数）和十进制数字（常用对数）。

下文中，按惯例将 p = 0 时的表达式p log p的值视为等于零，因为[math]\displaystyle{ \lim_{p \rightarrow 0+} p \log p = 0 }[/math]适用于任何对数底。

信源的熵

基于每个用于通信的源符号的概率质量函数，香农熵 Shannon Entropy（以比特为单位）由下式给出： [math]\displaystyle{ H = - \sum_{i} p_i \log_2 (p_i) }[/math]

其中p_i是源符号的第i个可能值出现的概率。该方程以比特（每个符号）为单位给出熵，因为它使用以2为底的对数。为表纪念，这个熵有时被称为香农熵。熵的计算也通常使用自然对数（以e为底数，其中e是欧拉数，其他底数也是可行的，但不常用），这样就可以测量每个符号的熵值，有时在公式中可以通过避免额外的常量来简化分析。例如以2⁸ = 256为底的对数，得出的值就以字节（而非比特）作为单位。以10为底的对数，每个符号将产生以十进制数字(或哈特利)为单位的测量值。

直观的来看，离散型随机变量X的熵H_X是对不确定性的度量，当只知道其分布时，它的值与X的值相关。

当一个信息源发出了一串含有N个符号的序列，且每个符号独立同分布时，其熵为N ⋅ H位(每个信息N符号)。 如果源数据符号是同分布但不独立的，则长度为N的消息的熵将小于N ⋅ H。

伯努利实验的熵，作为一个成功概率的函数，通常被称为二值熵函数, H_b(p)。当使用一个无偏的硬币做实验时，两个可能结果出现的概率相等，此时的熵值最大，为1。

如果一个人发送了1000比特（0s和1s），然而接收者在发送之前就已知这串比特序列中的每一个位的值，显然这个通信过程并没有任何信息（译注：如果你要告诉我一个我已经知到的消息，那么本次通信没有传递任何信息）。但是，如果消息未知，且每个比特独立且等可能的为0或1时，则本次通信传输了1000香农的信息（通常称为“比特”）。在这两个极端之间，信息可以按以下方式进行量化。如果𝕏是X可能在的所有消息的集合{x₁, ..., x_n}，且p(x)是[math]\displaystyle{ x \in \mathbb X }[/math]的概率，那么熵、H和H的定义如下:

[math]\displaystyle{ H(X) = \mathbb{E}_{X} [I(x)] = -\sum_{x \in \mathbb{X}} p(x) \log p(x). }[/math]

(其中:I(x)是自信息，表示单个信息的熵贡献;I(x)𝔼_X为X的期望。)熵的一个特性是，当消息空间中的所有消息都是等概率p(x) = 1/n时熵最大; 也就是说，在H(X) = log n这种情况下，熵是最不可预测的。

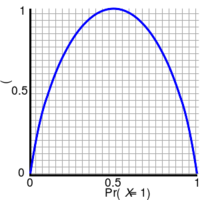
对于只有两种可能取值的随机变量的信息熵，其特殊情况为二值熵函数（通常用以为底2对数，因此以香农(Sh)为单位）：

[math]\displaystyle{ H_{\mathrm{b}}(p) = - p \log_2 p - (1-p)\log_2 (1-p). }[/math]

联合熵

两个离散的随机变量X和Y的联合熵 Joint Entropy大致是它们的配对: (X, Y)。若X和Y是独立的，那么它们的联合熵就是其各自熵的总和。

例如：如果(X, Y)代表棋子的位置（X 表示行和Y表示列），那么棋子所在位置的熵就是棋子行、列的联合熵。

[math]\displaystyle{ H(X, Y) = \mathbb{E}_{X,Y} [-\log p(x,y)] = - \sum_{x, y} p(x, y) \log p(x, y) \, }[/math]

尽管符号相似，注意联合熵与交叉熵不能混淆。

条件熵（含糊度）

在给定随机变量Y下X的条件熵 Conditional Entropy（或条件不确定性，也可称为X关于Y的含糊度)）是Y上的平均条件熵:

[math]\displaystyle{ H(X|Y) = \mathbb E_Y [H(X|y)] = -\sum_{y \in Y} p(y) \sum_{x \in X} p(x|y) \log p(x|y) = -\sum_{x,y} p(x,y) \log p(x|y). }[/math]

由于熵能够以随机变量或该随机变量的某个值为条件，所以应注意不要混淆条件熵的这两个定义（前者更为常用）。该类条件熵的一个基本属性为:

[math]\displaystyle{ H(X|Y) = H(X,Y) - H(Y) .\, }[/math]

互信息(转移信息)

互信息 Mutual Information度量的是某个随机变量在通过观察另一个随机变量时可以获得的信息量。在通信中可以用它来最大化发送和接收信号之间共享的信息量，这一点至关重要。X相对于Y的互信息由以下公式给出:

[math]\displaystyle{ I(X;Y) = \mathbb{E}_{X,Y} [SI(x,y)] = \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)\, p(y)} }[/math]

其中SI (Specific mutual Information，特定互信息)是点间的互信息。

互信息的一个基本属性是：

[math]\displaystyle{ I(X;Y) = H(X) - H(X|Y).\, }[/math]

也就是说，在编码X的过程中，知道Y比不知道Y平均节省I(X; Y)比特。

互信息是对称的:

[math]\displaystyle{ I(X;Y) = I(Y;X) = H(X) + H(Y) - H(X,Y).\, }[/math]

互信息可以表示为在给定Y值的情况下X的后验分布，以及X的先验概率分布之间的平均 Kullback-Leibler 散度(信息增益) :

[math]\displaystyle{ I(X;Y) = \mathbb E_{p(y)} [D_{\mathrm{KL}}( p(X|Y=y) \| p(X) )]. }[/math]

换句话说，这个指标度量：当我们给出Y的值，得出X上的概率分布将会平均变化多少。这通常用于计算边缘分布的乘积与实际联合分布的差异：

[math]\displaystyle{ I(X; Y) = D_{\mathrm{KL}}(p(X,Y) \| p(X)p(Y)). }[/math]

互信息与列联表中的似然比检验，多项分布，以及皮尔森卡方检验密切相关: 互信息可以视为评估一对变量之间独立性的统计量，并且具有明确指定的渐近分布。

散度(信息增益)

Kullback-Leibler 散度(或信息散度、相对熵、信息增益)是比较两种分布的方法: “真实的”概率分布p(X)和任意概率分布q(X)。若假设q(X)是基于某种方式压缩的数据的分布，而实际上p(X)才是真正分布，那么 Kullback-Leibler 散度是每个数据压缩所需的平均额外比特数。因此定义：

[math]\displaystyle{ D_{\mathrm{KL}}(p(X) \| q(X)) = \sum_{x \in X} -p(x) \log {q(x)} \, - \, \sum_{x \in X} -p(x) \log {p(x)} = \sum_{x \in X} p(x) \log \frac{p(x)}{q(x)}. }[/math]

尽管有时会将KL散度用作距离量度但它并不是一个真正的指标，因为它是不对称的，同时也不满足三角不等式(KL散度可以作为一个半准度量)。

KL散度的另一种解释是一种先验知识引入的“不必要的惊讶”。假设将从概率分布为“ p（x）”的离散集合中随机抽取数字“ X”，如果Alice知道真实的分布“p（x）”，而Bob（因为具有先验知识）认为概率分布是“q（x）”，那么在看到抽取出来的X的值后，平均而言，Bob将比Alice更加惊讶。KL散度就是Bob惊讶的期望值减去Alice惊讶的期望值（如果对数以2为底，则以比特为单位），这样Bob所拥有的先验知识的“错误的”程度可以用他“不必要的惊讶”的期望值来进行量化。

其他度量

信息论中其他重要的量包括瑞丽熵 Rényi Entropy(一种熵的推广)，微分熵(信息量推广到连续分布)，以及条件互信息。

编码理论

在可读CD的表面上显示划痕的图片。音乐和数据CD使用纠错编码进行编码，因此即使它们有轻微的划痕，也可以通过错误检测和纠正来对CD进行读取。

编码理论 Coding Theory是信息论最重要、最直接的应用之一，可以细分为信源编码理论 Source Coding Theory和信道编码理论 Channel Coding Theory。信息论使用统计学来量化描述数据所需的比特数，也就是源的信息熵。

• 数据压缩（源编码）：压缩问题有两个相关公式；

• 无损数据压缩：数据必须准确重构；

• 有损数据压缩：由失真函数测得的在指定保真度级别内分配重构数据所需的比特数。信息论中的这个部分称为率失真理论。

• 纠错码（信道编码）：数据压缩会尽可能多的消除冗余，而纠错码会添加所需的冗余（即纠错），以便在嘈杂的信道上有效且保真地传输数据。

信息传输定理，或着说“信源-信道分离定理”证明，编码理论应当划分为压缩和传输两部分。定理证明了在许多情况下使用比特作为信息的通用货币是合理的，但这只在发送用户与特定接收用户建立通信的情况下才成立。在具有多个发送器（多路访问信道），多个接收器（广播信道）或中转器（中继信道）或多个计算机网络的情况下，压缩后再进行传输可能就不再是最佳选择。网络信息论指的就是这些多主体通信模型。

信源理论

生成连续消息的任何过程都可以视为信息的通讯来源。无记忆信源是指每个消息都是独立同分布的随机变量，而遍历理论和平稳过程的性质对信源施加的限制较少。所有这些信源都可以看作随机的。在信息论领域外，这些术语也已经有很全面的相关研究。

速率

信息速率 Information Rate（熵率）是每个符号的平均熵。对于无记忆信源，信息速率仅表示每个符号的熵，而在平稳随机过程中，它是：

[math]\displaystyle{ r = \lim_{n \to \infty} H(X_n|X_{n-1},X_{n-2},X_{n-3}, \ldots); }[/math]

也就是，给定所有之前生成的符号下，一个符号的条件熵。对于非平稳的过程的更一般情况，平均速率为：

[math]\displaystyle{ r = \lim_{n \to \infty} \frac{1}{n} H(X_1, X_2, \dots X_n); }[/math]

也就是每个符号的联合熵的极限。对于平稳源，这两个表达式得出的结果相同。

在信息论中谈论一种语言的“速率”或“熵”是很常见的，也是很合适的，比如当信源是英文散文时。信息源的速率与其冗余度以及可被压缩程度有关。

信道容量

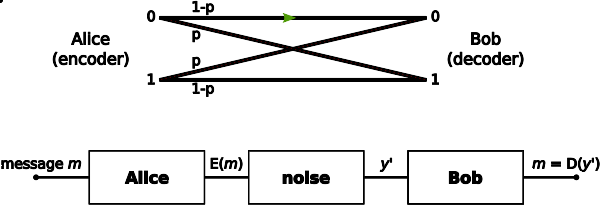
通过信道(例如，以太网电缆)进行通信是信息论的主要动机。然而，这样的信道往往不能产生信号的精确重建; 静默时段内、噪声、其他形式的信号损坏往往会使得信息质量的降低。

考虑离散信道上的通信过程。该过程的简单模型如下:

这里X表示要发送的信息的空间（全集），Y表示单位时间内通过信道接收的信息的空间。设p(y|x)是给定X的Y的条件概率分布函数。我们将p(y|x)视为通信信道的固定属性(表示信道噪声的性质)。那么X和Y的联合分布完全取决于所选用的信道和f(x)，以及通过信道发送的信息的边缘分布。在这些约束条件下，我们希望最大化信息速率或信号速率，可以通过信道进行通信。对此的适当度量为互信息，信道容量即为最大互信息，且由下式给出:

[math]\displaystyle{ C = \max_{f} I(X;Y).\! }[/math]

信道容量具有以下与以信息速率“R”进行通信有关的属性(其中“R”通常为每个符号的比特数)。对于任意信息速率R < C和编码错误ε > 0，存在足够大的长度为N和速率大于等于R的代码以及解码算法使得块错误的最大概率小于等于ε；即总是可以在任意小的块错误下进行传输。此外对于任何速率的“ R> C”，不可能以很小的块错误进行发送。

信道编码就寻找一种接近最优的编码，它可以用于在噪声信道上以接近信道容量的速率传输数据，且编码错误很小。

特定信道容量模型

• 连续时间内受高斯噪声（Gaussian noise）限制的模拟通信信道（详细内容请参见Shannon–Hartley定理）。

• 二进制对称通道（binary symmetric channel，BSC）是交叉概率为p的二进制输入、二进制输出（以概率p翻转输入位）通道。每个通道使用的BSC容量为1 − H_b(p)比特，其中H_b是以2为底的对数的二进制熵函数：

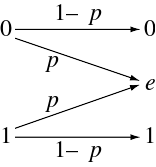
• 二进制擦除通道（binary erasure channel，BEC）是擦除概率为“ p”的二进制输入、三进制输出通道。可能的通道输出为0、1和擦除符号'e'。擦除表示信息输入位的完全丢失。每个通道使用的BEC容量为1 − p比特。

在其他领域的应用

情报使用和安全应用

信息论的概念可以应用于密码学和密码分析。在Ultra的项目中就使用了图灵的信息单位 ban，破解了德国的恩尼格玛密码，加速了二战在欧洲的结束。香农定义了一个重要的概念，现在称为单一性距离（unicity distance），基于明文的冗余性尝试给出具有唯一可解密性所需的最少量的密文。

信息论使我们觉得保密比最初看起来要困难得多。穷举法也可以破解基于非对称密钥算法或最常用的对称密钥算法(也称为密钥算法)，如分块加密。所有这些方法的安全性都来自以下假设：在一定的的时间内没有已知的攻击方法可以破解它们。

信息理论安全性指的是诸如一次性密钥之类的不易受到这种暴力攻击的方法。在这种情况下，可以确保明文和密文(以密钥为条件)之间的正条件互信息正确的传输，而明文和密文之间的无条件互信息仍为零，从而保证绝对安全的通信。换句话说，窃听者将无法通过获取密文而不是密钥的知识来改善其对原文本的猜测。但是，就像在其他任何密码系统中一样，即便时信息论中安全的方法必须小心正确的使用; 之所以Venona 项目能够破解苏联的一次性密钥，就是因为苏联不当地重复使用关键材料。

伪随机数的生成

伪随机数生成器在计算机语言库和应用程序中广泛应用。由于它们没有规避现代计算机设备和软件的确定性，因此普遍不适合用在密码学中。一类改进的随机数生成器称为加密安全的伪随机数生成器，但也需要软件外部的随机种子才能正常工作，这通过提取器来获得。用来度量提取器中充分随机性的概念是最小熵，该值通过瑞丽熵与香农熵关联；瑞丽熵还用于评估密码系统中的随机性。虽然相关，但具有较高香农熵的随机变量不一定适合在提取器中使用，因此也不能用在密码学中。

地震勘探

信息论的一个早期商业应用是在地震石油勘探领域。在该领域的应用可以从期望的地震信号中剔除和分离不需要的噪声。与以前的模拟方法相比，信息论和数字信号处理大大提高了图像的分辨率和清晰度。

符号学

符号学家Doede Nauta和Winfried Nöth都认为Charles Sanders Peirce在他的符号学著作中创造了信息论。 Nauta将符号信息论定义为研究编码、过滤和信息处理的内部过程。

信息论的概念（例如冗余和代码控制）已被符号学家如Umberto Eco和Ferruccio Rossi-Landi用来解释意识形态，将其作为消息传输的一种形式，占统治地位的社会阶层通过使用具有高度冗余性的标志来发出其信息，使得从符号中解码出来的消息只有一种，而不会时其他可能的消息。

其他应用

信息论在赌博、黑洞信息悖论和生物信息学中也有应用。

参见

• 算法概率
• 贝叶斯推断
• 通信理论
• 构造器理论 - 一种包含了量子信息的广义信息论
• 归纳概率
• 信息度量
• 最小消息长度
• 最小描述长度
• 重要文献列表
• 信息的哲学

应用

• 主动网络
• 密码分析
• 密码学
• 控制论
• 热力学和信息论中的熵
• 赌博
• 智能 (信息采集)
• 地震勘探

理论

• 编码理论
• 探测理论
• 估计理论
• 费舍尔理论
• 信息代数
• 信息不对称性
• 信息场论
• 信息几何
• 信息论于测度论
• 柯尔莫哥洛夫复杂度
• 信息论未解之谜（😂）
• 信息的逻辑
• 网络编码
• 信息的哲学
• 量子信息科学
• 信源编码

概念

• Ban (单位) —— 以10为底的对数信息量单位
• 信道容量
• 信道
• 信源
• 条件熵
• 转换信道
• 数据压缩
• 解码器
• 微分熵
• 可互换信息
• 信息波动复杂度
• 信息熵
• 联合熵
• Kullback–Leibler散度
• 互信息
• 点间互信息 (PMI)
• 接收器 (信息论)
• 冗余
• 瑞丽熵
• 子信息
• 单一性距离
• 种类
• 汉明距离

参考资料

经典之作

• Shannon, C.E. (1948), "A Mathematical Theory of Communication", Bell System Technical Journal, 27, pp. 379–423 & 623–656, July & October, 1948. PDF.
  Notes and other formats.

• R.V.L. Hartley, "Transmission of Information", Bell System Technical Journal, July 1928

• Andrey Kolmogorov (1968), "Three approaches to the quantitative definition of information" in International Journal of Computer Mathematics.

其他期刊文章

• J. L. Kelly, Jr., Betbubbles.comhttps://en.wikipedia.org/wiki/Defekte_Weblinks?dwl={{{url}}} Seite nicht mehr abrufbar], Suche in Webarchiven: Kategorie:Wikipedia:Weblink offline (andere Namensräume)[http://timetravel.mementoweb.org/list/2010/Kategorie:Wikipedia:Vorlagenfehler/Vorlage:Toter Link/URL_fehlt , "A New Interpretation of Information Rate" Bell System Technical Journal, Vol. 35, July 1956, pp. 917–26.

• R. Landauer, IEEE.org, "Information is Physical" Proc. Workshop on Physics and Computation PhysComp'92 (IEEE Comp. Sci.Press, Los Alamitos, 1993) pp. 1–4.

• Landauer, R. (1961). "Irreversibility and Heat Generation in the Computing Process" (PDF). IBM J. Res. Dev. 5 (3): 183–191. doi:10.1147/rd.53.0183.

• Timme, Nicholas; Alford, Wesley; Flecker, Benjamin; Beggs, John M. (2012). "Multivariate information measures: an experimentalist's perspective". arXiv:1111.6857 [cs.IT].

信息论教材

• Arndt, C. Information Measures, Information and its Description in Science and Engineering (Springer Series: Signals and Communication Technology), 2004,

• Ash, RB. Information Theory. New York: Interscience, 1965. New York: Dover 1990.

• Gallager, R. Information Theory and Reliable Communication. New York: John Wiley and Sons, 1968.

• Goldman, S. Information Theory. New York: Prentice Hall, 1953. New York: Dover 1968, 2005.

• Cover, Thomas; Thomas, Joy A. (2006). Elements of information theory (2nd ed.). New York: Wiley-Interscience. 

• Csiszar, I, Korner, J. Information Theory: Coding Theorems for Discrete Memoryless Systems Akademiai Kiado: 2nd edition, 1997.

• MacKay, David J. C.. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003.

• Mansuripur, M. Introduction to Information Theory. New York: Prentice Hall, 1987.

• McEliece, R. The Theory of Information and Coding". Cambridge, 2002.

• Pierce, JR. "An introduction to information theory: symbols, signals and noise". Dover (2nd Edition). 1961 (reprinted by Dover 1980).

• Reza, F. An Introduction to Information Theory. New York: McGraw-Hill 1961. New York: Dover 1994.

• Shannon, Claude; Weaver, Warren (1949). The Mathematical Theory of Communication. Urbana, Illinois: University of Illinois Press. LCCN 49-11922. http://monoskop.org/images/b/be/Shannon_Claude_E_Weaver_Warren_The_Mathematical_Theory_of_Communication_1963.pdf. 

• Stone, JV. Chapter 1 of book "Information Theory: A Tutorial Introduction", University of Sheffield, England, 2014.

• Yeung, RW. A First Course in Information Theory Kluwer Academic/Plenum Publishers, 2002.

• Yeung, RW. Information Theory and Network Coding Springer 2008, 2002.

其他书籍

• Leon Brillouin, Science and Information Theory, Mineola, N.Y.: Dover, [1956, 1962] 2004.

• James Gleick, The Information: A History, a Theory, a Flood, New York: Pantheon, 2011.

• A. I. Khinchin, Mathematical Foundations of Information Theory, New York: Dover, 1957.

• H. S. Leff and A. F. Rex, Editors, Maxwell's Demon: Entropy, Information, Computing, Princeton University Press, Princeton, New Jersey (1990).

• Robert K. Logan. What is Information? - Propagating Organization in the Biosphere, the Symbolosphere, the Technosphere and the Econosphere, Toronto: DEMO Publishing.

• Tom Siegfried, The Bit and the Pendulum, Wiley, 2000.

• Charles Seife, Decoding the Universe, Viking, 2006.

• Jeremy Campbell, Grammatical Man, Touchstone/Simon & Schuster, 1982,

• Henri Theil, Economics and Information Theory, Rand McNally & Company - Chicago, 1967.

• Escolano, Suau, Bonev, Information Theory in Computer Vision and Pattern Recognition, Springer, 2009.

• Vlatko Vedral, Decoding Reality: The Universe as Quantum Information, Oxford University Press 2010.

信息论大型开放式课程

• Raymond W. Yeung, "Information Theory" (The Chinese University of Hong Kong)

外部链接

• Lambert F. L. (1999), "Shuffled Cards, Messy Desks, and Disorderly Dorm Rooms - Examples of Entropy Increase? Nonsense!", Journal of Chemical Education

• IEEE Information Theory Society and ITSOC Monographs, Surveys, and Reviews

编者推荐

集智俱乐部

集智文章推荐

计算美学前沿速递：用信息论“重新发现”风景画艺术史

美术研究中的一个核心问题是，不同年代和流派的绘画作品，在组织架构上，是否有着相似之处？2020年10月发表在美国国家科学院院刊PNAS的论文中，研究者通过信息论和网络分析，对来自61个国家，1476名画家总计14912幅西方风景画的研究，证实了该假说。

Science前沿：用信息论解释动植物间的军备竞赛

在植物与植食性昆虫组成的生态系统中，不同物种在相互作用的过程中， 彼此适应，形成了一个相互影响的协同适应系统。近期Sicence的一项研究从气味信息的角度，讨论动植物协同进化中的军备竞赛，对研究生态网络内部的交流机制很有启发。同期的一篇相关评论文章对该话题进行了全新解答，本文是该评论文章的编译。

---

本中文词条由Moonscar参与编译， Qige96、Ricky 审校，不是海绵宝宝、唐糖糖编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。