遗传算法
遗传算法 Genetic Algorithms 的基础是“染色体是一串基因”这一经典观点。R.A. 费舍尔 使用这种观点建立了数理遗传学 Mathematical Genetics ,提供了数学公式来说明特定基因在整个种群中的扩散速率(Fisher,1958)。 费舍尔的工作可以总结为以下关键要点:
- 染色体每个位置的一组可以相互替代的基因(等位基因),从而指定了所有可能的基因串(染色体)。
- 一代又一代的进化观,在每个阶段,一群个体生产一组后代个体,构成了下一代。
- 一个适应度函数,计算携带某个染色体的个体能贡献的后代数量。
- 一组遗传算子,特别是Fisher的形式化中的突变算子,可以改变个体的后代,从而使下一代不同于当前一代。
在这种表述中,自然选择 Natural Selection可以被认为是一种搜索方法,用以搜索可能个体集合(即搜索空间),以找到具有更高适应度的个体。即使当自然种群仅由一个物种组成时(例如,当前这一代人类),该种群中也存在相当大的差异。 这些变体就构成搜索空间的所有样本。
定义
遗传算法是Fisher公式的一种泛化后的计算机程序版本(Holland J, 1995),泛化的要点包括:
- 关注染色体上基因的交互,而非假设等位基因相互独立起作用,以及
- 一套更广泛的遗传算子,包括了交叉 crossing-over(重组 recombination)和倒位 inversion等著名的遗传算子。
上述第一种泛化使得适应度函数变成了一个复杂的非线性函数,不能再简单地用各个基因效应的加和来近似。第二种泛化则强调了像交叉这种作用于染色体的常见遗传算子。交叉操作在每一次染色体配对中都会出现,而变异操作则在每一百万个个体中才可能出现一次。交叉是哺乳动物能产生混合了亲代特征的子代的核心原因。人类群体就是最生动的例证。交叉还使得使用人工杂交育种来创造出具有优良特征的变种动植物成为可能。很显然,交叉的高频出现使得它成为演化中的一个重要角色,以及遗传算法中的一个关键步骤。
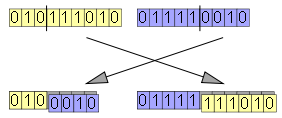
交叉算子的最简单形式(单点交叉)可以被很容易的定义:两条染色体对齐排列好,随机选择染色体上的一点,两条染色体交换从该点起直到末尾的这一段,从而生成了两个后代染色体。
这种简单版本的交叉操作能很好地近似在实际的配对中出现的交叉现象。在单点交叉的作用下,同一条染色体中,相距较近的等位基因可能会被分配到同一个后代中,而相距较远的等位基因则更可能被分割开来,分配到不同的后代中。比如,在一条有1001个等位基因的染色体中,只有1/1001的概率使得一堆邻近的等位基因被分隔开,而在染色体头尾两端的基因则总是会被分割开来。在标准的遗传学术语中,这种现象叫做 连锁 linkage。通过观察由等位基因决定的性状在后代中被分割的频率,连锁现象就可以被确定。事实上,假设单点交叉就能让基因测序变得可能,即便我们没有任何关于DNA的知识——在1944年,使用实验方法来确定连锁效应,华盛顿卡内基研究所 Carnegie Institution of Washington 就发表了一大本记录了果蝇基因序列的手册(Lindsley & Grell, 1944)。
在费舍尔的工作基础上,遗传算法使用了不同的适应度。但是遗传算法着重强调了由交叉算子产生的变异。基本的遗传算法程序通过下列步骤来根据当代群体产生后代群体(为简单起见,假设每一个个体都只有一个染色体):
- 从有[math]\displaystyle{ N }[/math]个等位基因串的群体开始(最初可能是随机产生的)
- 随机从当代群体中选择两个个体,有更高适应度的个体更可能被选中
- 使用交叉算子(偶尔用一下变异算子)来产生两个新的个体,这两个新个体会参与组成下一代群体
- 重复步骤(2)和(3)[math]\displaystyle{ N/2 }[/math]次,产生新一代N个个体。
- 回到步骤(1),根据新一代群体来继续产生后代
当然,可以有很多种修改这些步骤的方法,但这个基本的流程已经展示了遗传算法的基本性质。
交叉
交叉算子在后续世代的研究中引入了大量的复杂性:在亲代中极其有效的个体(比如爱因斯坦)在后代中不会出现,因为该个体中地等位基因被分割开来,传到了不同的后代个体中。这就引发了一个重要的问题:如果不是亲代的染色体,那到底是什么在一代又一代中遗传着呢?回答这个问题,需要预测在一代又一代中扩散的等位基因团,还需要对费舍尔的基本理论做进一步的扩展和泛化。模式定理 Schema Theorem 就是这么一个泛化。模式定理把任意一个等位基因团成为“模式”。一个模式使用符号 * 来表示染色体中不属于该模式的位置。例如,如果一个位置中有两个不同的等位基因,分别为1和0,那么位置2为1,位置4为0,位置5为0的基因团就被表示成符号串*1*00**...*。用 N(s,t) 表示在第t代中携带模式s的染色体数目模式定理揭示了携带模式s的染色体在下一代中预期的数目[math]\displaystyle{ N(s,t+1) }[/math]。下面是一个简化后的版本:
[math]\displaystyle{ N(s,t+1) = u(s,t)[1-e]N(s,t) }[/math]
其中 [math]\displaystyle{ u(s,t) }[/math] 指在第[math]\displaystyle{ t }[/math]代中携带模式[math]\displaystyle{ s }[/math]的染色体的平均适应度, [math]\displaystyle{ e }[/math] 指模式s会被变异算子和交叉算子破坏的概率(通常会很小,但如果模式中的等位基因在染色体中分布很广,即模式的长度很大,则[math]\displaystyle{ e }[/math]会很大)。上述公式可以被重写为一个概率值形式 [math]\displaystyle{ P(s,t)\ , }[/math],这是在数理遗传学中更加典型的形式:[math]\displaystyle{ P(s,t) = N(s,t)/N(t)\ , }[/math] ,其中[math]\displaystyle{ N(t) }[/math]是群体在第[math]\displaystyle{ t\ . }[/math]代的规模。
模式定理说明了,群体中每一个等位基因团的比例都会提高或降低,其速率由它所能带来的平均适应度决定。特别地,能带来更高适应度的模式,会在群体中快速传播开来。结果就是,交叉算子会使用这些高于平均适应度的模式,尝试各种新的组合。这些模式成为了构建解的组件块 building blocks。尽管遗传算法每一代只处理[math]\displaystyle{ N(t) }[/math]个符号串,它能有效处理在群体中承载的多得多的模式。比如,一个长度为40的符号串中包含的模式的数量为[math]\displaystyle{ 2 * exp(40) \sim 16,000\ , }[/math],因此遗传算法只要处理几十个长度为40的符号串,就能处理成千上万个模式。这是一个及其出色的速度。
应用
遗传算法经常被用于为那些没有标准解法(如梯度上升、相加近似)的问题寻找一个好的解(Mitchell, 2009)。一些已经应用了遗传算法的典型问题包括控制流设计、飞机引擎设计、规划、蛋白质折叠、机器学习、对语言的获取和演化建模、以及对复杂适应系统(例如市场和生态系统)建模等。要使用遗传算法,搜索空间必须被表示成用一个固定符号集生成的一组符号序列,就像生物的染色体只由四种碱基构成一样。这些符号串可以表示任何事物,从生物体,到信号处理规则,到复杂实应系统中的智能体等。遗传算法要初始化一个由这些符号串组成的群体,这可以用随机的方式生成,也可以用一些关于问题的先验知识来生成。然后,遗传算法就会处理这些符号串,后续的世代就会显示出一些模式,这些模式能是个体拥有高于平均值的适应度。当高于平均、优良连接的模式频繁地出现时,遗传算法就会迅速发现并用来优化。
代码实现
关于遗传算法的代码实现,可以参考使用pythony实现遗传算法这一词条。
引用
- R.A., Fisher (1958). The Genetical Theory of Natural Selection Oxford University Press : .
- J. H., Holland (1995). Hidden Order: How Adaptation Builds Complexity Addison-Wesley, Redwood City, CA..
- D.L., Lindsley and E.H., Grell (1944). Genetic Variations of Drosophila Melanogaster Carnegie Institution of Washington. : .
- M., Mitchell (2009). Complexity: A Guided Tour. Oxford University Press, New York, NY.
本中文词条由用户Ricky参与翻译、审校、编辑,欢迎在讨论页面留言。
本词条内容源自scholarpedia及公开资料,遵守 CC3.0协议。