自相似

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

Notoc

A Koch curve has an infinitely repeating self-similarity when it is magnified. 当无限放大科赫曲线时，它会展示出无限重复的自相似性。

A Koch curve has an infinitely repeating self-similarity when it is magnified.

[[[科赫曲线被放大后有无限重复的自相似性]]

Standard (trivial) self-similarity.^[1]标准(平凡)自相似性。^[1]

Standard (trivial) self-similarity.

标准(平凡)自相似性。

This vocabulary was introduced by Benoit Mandelbrot in 1964. In mathematics, a self-similar object is exactly or approximately similar to a part of itself (i.e. the whole has the same shape as one or more of the parts). Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales.^[2] Self-similarity is a typical property of fractals. Scale invariance is an exact form of self-similarity where at any magnification there is a smaller piece of the object that is similar to the whole. For instance, a side of the Koch snowflake is both symmetrical and scale-invariant; it can be continually magnified 3x without changing shape. The non-trivial similarity evident in fractals is distinguished by their fine structure, or detail on arbitrarily small scales. As a counterexample, whereas any portion of a straight line may resemble the whole, further detail is not revealed.

自相似一词由本华·曼德勃罗与1964年引入。（标注：此处将后文的一句移过来以使行文看起来更连贯。）在数学中，一个自相似的物体与它自身的某一部分完全或近似地相似（例如：整体和一个或多个部分具有相同的形状）。现实世界中的许多物体，例如海岸线，在统计学上是自相似的：它们的某些部分在许多不同尺度上表现出相同的统计特性。自相似是分形的一个典型性质。标度不变性是自相似的一种精确形式：在任何放大倍数下，物体中总有更小的部分与整体相似。例如，科赫雪花的一边既对称又具有标度不变性；它可以连续放大3倍而不改变形状。分形中明显的非平凡的相似性是通过它们的精细结构或任意小尺度上的细节来区分的。对比一个反例来看，尽管直线的任何部分都可能类似于整体，但是进一步放大之后，却没有更多的细节显露。

A time developing phenomenon is said to exhibit self-similarity if the numerical value of certain observable quantity [math]\displaystyle{ f(x,t) }[/math] measured at different times are different but the corresponding dimensionless quantity at given value of [math]\displaystyle{ x/t^z }[/math] remain invariant. It happens if the quantity [math]\displaystyle{ f(x,t) }[/math] exhibits dynamic scaling. The idea is just an extension of the idea of similarity of two triangles.^[3]^[4]^[5] Note that two triangles are similar if the numerical values of their sides are different however the corresponding dimensionless quantities, such as their angles, coincide.

A time developing phenomenon is said to exhibit self-similarity if the numerical value of certain observable quantity [math]\displaystyle{ f(x,t) }[/math] measured at different times are different but the corresponding dimensionless quantity at given value of [math]\displaystyle{ x/t^z }[/math] remain invariant. It happens if the quantity [math]\displaystyle{ f(x,t) }[/math] exhibits dynamic scaling. The idea is just an extension of the idea of similarity of two triangles. Note that two triangles are similar if the numerical values of their sides are different however the corresponding dimensionless quantities, such as their angles, coincide.

对于一个依赖时间发展的现象，如果其相关观测量[math]\displaystyle{ f(x,t) }[/math]在不同时间所测得的数值不同，但是对应的无量纲量在给定的[math]\displaystyle{ x/t^z }[/math]下保持不变，则可以说该现象具有自相似性。通常如果[math]\displaystyle{ f(x,t) }[/math]显示出Dynamic Scaling 动态缩放就会出现这种情况。这也是相似三角形概念的拓展和延伸。值得注意的是，即使两个三角形的边长不同，但他们的内角相等，则他们也是相似的。

Peitgen et al. explain the concept as such:

If parts of a figure are small replicas of the whole, then the figure is called self-similar....A figure is strictly self-similar if the figure can be decomposed into parts which are exact replicas of the whole. Any arbitrary part contains an exact replica of the whole figure.

佩特根等曾这样解释这一概念：

如果一个图形的部分是整体的小尺度复制品，就可以认为这一图形是自相似的；如果图形分解产生的部分都是该图形的精确复制，则这个图形是严格自相似的。任何任意的部分都包含整个图形的精确复制。

Since mathematically, a fractal may show self-similarity under indefinite magnification, it is impossible to recreate this physically. Peitgen et al. suggest studying self-similarity using approximations:

In order to give an operational meaning to the property of self-similarity, we are necessarily restricted to dealing with finite approximations of the limit figure. This is done using the method which we will call box self-similarity where measurements are made on finite stages of the figure using grids of various sizes.

即使从数学上来说，分形可以在无限放大的条件下显示出自相似性，但是这在物理上是不可能实现的。佩特根等建议使用近似方法来研究自相似性：

为了使自相似的性质具有操作意义，我们必须处理有限图形的有限近似。这可以采取盒子自相似性方法来解决，即使用不同尺寸的格子对图形的有限阶段进行测量。

/* Styling for Template:Quote */ .templatequote { overflow: hidden; margin: 1em 0; padding: 0 40px; } .templatequote .templatequotecite {

   line-height: 1.5em;
   /* @noflip */
   text-align: left;
   /* @noflip */
   padding-left: 1.6em;
   margin-top: 0;

}

/* Styling for Template:Quote */ .templatequote { overflow: hidden; margin: 1em 0; padding: 0 40px; } .templatequote .templatequotecite {

   line-height: 1.5em;
   /* @noflip */
   text-align: left;
   /* @noflip */
   padding-left: 1.6em;
   margin-top: 0;

}

Self-affinity 自仿射性

! -- 自我关联直接重定向到这里 --

A self-affine fractal with Hausdorff dimension=1.8272. 图示为一个自仿射分形，其豪斯多夫维数为1.8272.

A self-affine fractal with Hausdorff dimension=1.8272.

一个自仿射分形[豪斯多夫维数1.8272. ]

In mathematics, self-affinity is a feature of a fractal whose pieces are scaled by different amounts in the x- and y-directions. This means that to appreciate the self similarity of these fractal objects, they have to be rescaled using an anisotropic affine transformation.

在数学中，自仿射性是分形的特征之一，分形的各部分在 x 方向和 y 方向上按不同的比例缩放。这意味着要理解这些分形对象的自相似性，必须使用Anisotropic Affine Transformation 各向异性仿射变换进行缩放。

Definition 定义

A compact topological space X is self-similar if there exists a finite set S indexing a set of non-surjective homeomorphisms [math]\displaystyle{ \{ f_s : s\in S \} }[/math] for which

如果存在一个有限集 S 对[math]\displaystyle{ \{ f_s : s\in S \} }[/math]中的一组非满射同胚集进行索引，则紧致拓扑空间 X 是自相似的，有：

[math]\displaystyle{ X=\bigcup_{s\in S} f_s(X) }[/math]

If [math]\displaystyle{ X\subset Y }[/math], we call X self-similar if it is the only non-empty subset of Y such that the equation above holds for [math]\displaystyle{ \{ f_s : s\in S \} }[/math]. We call

假设有

[math]\displaystyle{ X\subset Y }[/math]，

当且仅当X是Y的唯一非空子集，使得上式对

[math]\displaystyle{ \{ f_s : s\in S \} }[/math]

成立，则X是自相似的。而且我们称

[math]\displaystyle{ \mathfrak{L}=(X,S,\{ f_s : s\in S \} ) }[/math]

是自相似结构。

a self-similar structure. The homeomorphisms may be iterated, resulting in an iterated function system. The composition of functions creates the algebraic structure of a monoid. When the set S has only two elements, the monoid is known as the dyadic monoid. The dyadic monoid can be visualized as an infinite binary tree; more generally, if the set S has p elements, then the monoid may be represented as a p-adic tree.

一个自相似的结构。同胚可以迭代，产生迭代函数系统。函数的组合产生了幺半群的代数结构。当集合S只有两个元素时，幺半群此时称为二元幺半群。二元幺半群可以表示为无限二叉树；更一般地说，如果集合S有p个元素，则一元类可以表示为p进树。

The automorphisms of the dyadic monoid is the modular group; the automorphisms can be pictured as hyperbolic rotations of the binary tree.

二元幺半群的自同构是模群，自同构可以描述为二叉树的双曲旋转。

A more general notion than self-similarity is Self-affinity.

比自相似性更一般的概念是自仿射性。

Examples

Self-similarity in the Mandelbrot set shown by zooming in on the Feigenbaum point at (−1.401155189..., 0)

在[[ Mandelbrot 集合放大 Feigenbaum 点在(- 1.401155189... ，0)]中的自相似性

An image of the Barnsley fern which exhibits affine self-similarity

仿射图[展现仿射自相似性的巴恩斯利蕨类植物]的图像

The Mandelbrot set is also self-similar around Misiurewicz points.

曼德尔布罗特集合在 Misiurewicz 点附近也具有自相似性。

Self-similarity has important consequences for the design of computer networks, as typical network traffic has self-similar properties. For example, in teletraffic engineering, packet switched data traffic patterns seem to be statistically self-similar.^[6] This property means that simple models using a Poisson distribution are inaccurate, and networks designed without taking self-similarity into account are likely to function in unexpected ways.

Self-similarity has important consequences for the design of computer networks, as typical network traffic has self-similar properties. For example, in teletraffic engineering, packet switched data traffic patterns seem to be statistically self-similar. This property means that simple models using a Poisson distribution are inaccurate, and networks designed without taking self-similarity into account are likely to function in unexpected ways.

自相似性对于计算机网络的设计有着重要的影响，因为典型的网络流量具有自相似的特性。例如，在远程通信工程中，分组交换数据通信模式在统计学上似乎是自相似的。这个特性意味着使用泊松分佈的简单模型是不准确的，而且在设计网络时没有考虑自相似性，网络很可能以意想不到的方式运行。

Similarly, stock market movements are described as displaying self-affinity, i.e. they appear self-similar when transformed via an appropriate affine transformation for the level of detail being shown.引用错误：没有找到与</ref>对应的<ref>标签 Andrew Lo describes stock market log return self-similarity in econometrics.^[7]

date=February 1999| authorlink=Benoit Mandelbrot}}</ref> Andrew Lo describes stock market log return self-similarity in econometrics.

日期1999年2月 | authorlink 本华·曼德博} / ref Andrew Lo 在计量经济学中描述了股票市场日志返回自相似性。

Finite subdivision rules are a powerful technique for building self-similar sets, including the Cantor set and the Sierpinski triangle.

有限细分规则是建立自相似集的一种强大技术，包括 Cantor 集和谢尔宾斯基三角形集。

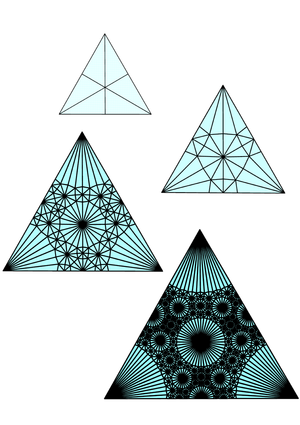
A triangle subdivided repeatedly using barycentric subdivision. The complement of the large circles becomes a Sierpinski carpet

使用[[重心细分]重复细分的三角形。大圆圈的补充变成了谢尔宾斯基地毯

In cybernetics

The Viable System Model of Stafford Beer is an organizational model with an affine self-similar hierarchy, where a given viable system is one element of the System One of a viable system one recursive level higher up, and for whom the elements of its System One are viable systems one recursive level lower down.

斯塔福德 · 比尔的可行系统模型是一个具有仿射自相似层次结构的组织模型，其中给定的可行系统是一个可行系统的一个元素，一个递归层次更高的可行系统的一个元素，对于这个系统的元素是一个递归层次更低的可行系统。

In nature

Close-up of a Romanesco broccoli.

宝塔花菜的特写镜头

模板:Further

Self-similarity can be found in nature, as well. To the right is a mathematically generated, perfectly self-similar image of a fern, which bears a marked resemblance to natural ferns. Other plants, such as Romanesco broccoli, exhibit strong self-similarity.

自相似性也存在于自然界中。右边是一个数学生成的完全自相似的蕨类植物图像，它与天然蕨类植物有明显的相似之处。其他植物，如宝塔花菜，表现出很强的自相似性。

In music

Strict canons display various types and amounts of self-similarity, as do sections of fugues.

A Shepard tone is self-similar in the frequency or wavelength domains.

The Danish composer Per Nørgård has made use of a self-similar integer sequence named the 'infinity series' in much of his music.

In the research field of music information retrieval, self-similarity commonly refers to the fact that music often consists of parts that are repeated in time.^[8] In other words, music is self-similar under temporal translation, rather than (or in addition to) under scaling.^[9]

References

↑ ^1.0 ^1.1 Mandelbrot, Benoit B. (1982). The Fractal Geometry of Nature, p.44.

.

↑ Mandelbrot, Benoit B. (5 May 1967). "How long is the coast of Britain? Statistical self-similarity and fractional dimension". Science. New Series. 156 (3775): 636–638. Bibcode:1967Sci...156..636M. doi:10.1126/science.156.3775.636. PMID 17837158. PDF
↑ Hassan M. K., Hassan M. Z., Pavel N. I. (2011). "Dynamic scaling, data-collapseand Self-similarity in Barabasi-Albert networks". J. Phys. A: Math. Theor. 44 (17): 175101. arXiv:1101.4730. Bibcode:2011JPhA...44q5101K. doi:10.1088/1751-8113/44/17/175101.{{cite journal}}: CS1 maint: multiple names: authors list (link)
↑ Hassan M. K., Hassan M. Z. (2009). "Emergence of fractal behavior in condensation-driven aggregation". Phys. Rev. E. 79 (2): 021406. arXiv:0901.2761. Bibcode:2009PhRvE..79b1406H. doi:10.1103/physreve.79.021406. PMID 19391746.
↑ Dayeen F. R., Hassan M. K. (2016). "Multi-multifractality, dynamic scaling and neighbourhood statistics in weighted planar stochastic lattice". Chaos, Solitons & Fractals. 91: 228. arXiv:1409.7928. Bibcode:2016CSF....91..228D. doi:10.1016/j.chaos.2016.06.006.
↑ Leland, W.E.; Taqqu, M.S.; et al. (January 1995). "On the self-similar nature of Ethernet traffic (extended version)" (PDF). IEEE/ACM Transactions on Networking. 2 (1): 1–15. doi:10.1109/90.282603.

↑ Campbell, Lo and MacKinlay (1991) "Econometrics of Financial Markets ", Princeton University Press!

↑ Foote, Jonathan (30 October 1999). Visualizing music and audio using self-similarity. pp. 77–80. doi:10.1145/319463.319472. ISBN 978-1581131512. http://musicweb.ucsd.edu/~sdubnov/CATbox/Reader/p77-foote.pdf.
↑ Pareyon, Gabriel (April 2011). On Musical Self-Similarity: Intersemiosis as Synecdoche and Analogy. International Semiotics Institute at Imatra; Semiotic Society of Finland. p. 240. ISBN 978-952-5431-32-2. Archived from the original on 8 February 2017. https://web.archive.org/web/20170208034152/https://tuhat.helsinki.fi/portal/files/15216101/Pareyon_Dissertation.pdf. Retrieved 30 July 2018. (Also see Google Books)

External links

"Copperplate Chevrons" — a self-similar fractal zoom movie

"Self-Similarity" — New articles about Self-Similarity. Waltz Algorithm

Self-affinity

Mandelbrot, Benoit B. (1985). "Self-affinity and fractal dimension" (PDF). Physica Scripta. 32 (4): 257–260. Bibcode:1985PhyS...32..257M. doi:10.1088/0031-8949/32/4/001.

Sapozhnikov, Victor; Foufoula-Georgiou, Efi (May 1996). "Self-Affinity in Braided Rivers" (PDF). Water Resources Research. 32 (5): 1429–1439. doi:10.1029/96wr00490. Archived (PDF) from the original on 30 July 2018. Retrieved 30 July 2018.

Benoît B. Mandelbrot (2002). Gaussian Self-Affinity and Fractals: Globality, the Earth, 1/F Noise, and R/S. ISBN 978-0387989938.

模板:Fractals

Category:Fractals

分类: 分形

Category:Scaling symmetries

类别: 缩放对称性

Category:Homeomorphisms

范畴: 同胚

Category:Self-reference

类别: 自我参照

This page was moved from wikipedia:en:Self-similarity. Its edit history can be viewed at 自相似/edithistory

[:0-1] 1.0 ^1.1 Mandelbrot, Benoit B. (1982). The Fractal Geometry of Nature, p.44.
v
t
e
Inline tags
Attribution

{{Attribution needed}}

{{By whom}}

{{Weasel-inline}}

{{Which?}}

{{Who}}

Citation

{{Better source}}

{{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

{{Citation needed (lead)}}

{{Failed verification}}

{{Full}}

{{Primary source-inline}}

{{Request quotation}}

{{Retracted}}

{{Third-party-inline}}

Incomplete

{{Author missing}}

{{Author incomplete}}

{{Date missing}}

{{ISBN missing}}

{{Page needed}}

{{Publisher missing}}

{{Title incomplete}}

{{Year missing}}

{{Dead link}}

Content

{{Contradict-inline}}

{{Contradiction-inline}}

{{Dubious|talk page section name}}

{{Examples}}

{{Inconsistent}}

{{List fact}}

{{Lopsided}}

{{POV-statement}}

Date and place

{{Clarify timeframe}}

{{Quantify}}

{{Update after}}

{{Update-small}}

{{When}}

{{Where}}

{{Year needed}}

Wikification

{{Disambiguation needed}}

{{Pronunciation needed}}

Wording

{{Ambiguous}}

{{Awkward}}

{{Buzz}}

{{Clarify}}

{{Clarify span}}

{{Definition}}

{{Elucidate}}

{{Expand acronym}}

{{Technical-statement}}

{{Vague|optional message to be displayed on mouseover}}

{{Why?}}

Category
.

[2] v

[3] t

[4] e

[5] {{Attribution needed}}

[6] {{By whom}}

[7] {{Weasel-inline}}

[8] {{Which?}}

[9] {{Who}}

[10] {{Better source}}

[11] {{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

[12] {{Citation needed span}}

[13] {{Reference necessary}}

[14] {{Citation needed (lead)}}

[15] {{Failed verification}}

[16] {{Full}}

[17] {{Primary source-inline}}

[18] {{Request quotation}}

[19] {{Retracted}}

[20] {{Third-party-inline}}

[21] {{Author missing}}

[22] {{Author incomplete}}

[23] {{Date missing}}

[24] {{ISBN missing}}

[25] {{Page needed}}

[26] {{Publisher missing}}

[27] {{Title incomplete}}

[28] {{Year missing}}

[29] {{Dead link}}

[30] {{Contradict-inline}}

[31] {{Contradiction-inline}}

[32] {{Dubious|talk page section name}}

[33] {{Examples}}

[34] {{Inconsistent}}

[35] {{List fact}}

[36] {{Lopsided}}

[37] {{POV-statement}}

[38] {{Clarify timeframe}}

[39] {{Quantify}}

[40] {{Update after}}

[41] {{Update-small}}

[42] {{When}}

[43] {{Where}}

[44] {{Year needed}}

[45] {{Disambiguation needed}}

[46] {{Pronunciation needed}}

[47] {{Ambiguous}}

[48] {{Awkward}}

[49] {{Buzz}}

[50] {{Clarify}}

[51] {{Clarify span}}

[52] {{Definition}}

[53] {{Elucidate}}

[54] {{Expand acronym}}

[55] {{Technical-statement}}

[56] {{Vague|optional message to be displayed on mouseover}}

[57] {{Why?}}

[Mandelbrot_Science_1967-2] Mandelbrot, Benoit B. (5 May 1967). "How long is the coast of Britain? Statistical self-similarity and fractional dimension". Science. New Series. 156 (3775): 636–638. Bibcode:1967Sci...156..636M. doi:10.1126/science.156.3775.636. PMID 17837158. PDF

[3] Hassan M. K., Hassan M. Z., Pavel N. I. (2011). "Dynamic scaling, data-collapseand Self-similarity in Barabasi-Albert networks". J. Phys. A: Math. Theor. 44 (17): 175101. arXiv:1101.4730. Bibcode:2011JPhA...44q5101K. doi:10.1088/1751-8113/44/17/175101.{{cite journal}}: CS1 maint: multiple names: authors list (link)

[4] Hassan M. K., Hassan M. Z. (2009). "Emergence of fractal behavior in condensation-driven aggregation". Phys. Rev. E. 79 (2): 021406. arXiv:0901.2761. Bibcode:2009PhRvE..79b1406H. doi:10.1103/physreve.79.021406. PMID 19391746.

[5] Dayeen F. R., Hassan M. K. (2016). "Multi-multifractality, dynamic scaling and neighbourhood statistics in weighted planar stochastic lattice". Chaos, Solitons & Fractals. 91: 228. arXiv:1409.7928. Bibcode:2016CSF....91..228D. doi:10.1016/j.chaos.2016.06.006.

[6] Leland, W.E.; Taqqu, M.S.; et al. (January 1995). "On the self-similar nature of Ethernet traffic (extended version)" (PDF). IEEE/ACM Transactions on Networking. 2 (1): 1–15. doi:10.1109/90.282603.

[7] Campbell, Lo and MacKinlay (1991) "Econometrics of Financial Markets ", Princeton University Press!
v
t
e
Inline tags
Attribution

{{Attribution needed}}

{{By whom}}

{{Weasel-inline}}

{{Which?}}

{{Who}}

Citation

{{Better source}}

{{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

{{Citation needed (lead)}}

{{Failed verification}}

{{Full}}

{{Primary source-inline}}

{{Request quotation}}

{{Retracted}}

{{Third-party-inline}}

Incomplete

{{Author missing}}

{{Author incomplete}}

{{Date missing}}

{{ISBN missing}}

{{Page needed}}

{{Publisher missing}}

{{Title incomplete}}

{{Year missing}}

{{Dead link}}

Content

{{Contradict-inline}}

{{Contradiction-inline}}

{{Dubious|talk page section name}}

{{Examples}}

{{Inconsistent}}

{{List fact}}

{{Lopsided}}

{{POV-statement}}

Date and place

{{Clarify timeframe}}

{{Quantify}}

{{Update after}}

{{Update-small}}

{{When}}

{{Where}}

{{Year needed}}

Wikification

{{Disambiguation needed}}

{{Pronunciation needed}}

Wording

{{Ambiguous}}

{{Awkward}}

{{Buzz}}

{{Clarify}}

{{Clarify span}}

{{Definition}}

{{Elucidate}}

{{Expand acronym}}

{{Technical-statement}}

{{Vague|optional message to be displayed on mouseover}}

{{Why?}}

Category

[64] v

[65] t

[66] e

[67] {{Attribution needed}}

[68] {{By whom}}

[69] {{Weasel-inline}}

[70] {{Which?}}

[71] {{Who}}

[72] {{Better source}}

[73] {{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

[74] {{Citation needed span}}

[75] {{Reference necessary}}

[76] {{Citation needed (lead)}}

[77] {{Failed verification}}

[78] {{Full}}

[79] {{Primary source-inline}}

[80] {{Request quotation}}

[81] {{Retracted}}

[82] {{Third-party-inline}}

[83] {{Author missing}}

[84] {{Author incomplete}}

[85] {{Date missing}}

[86] {{ISBN missing}}

[87] {{Page needed}}

[88] {{Publisher missing}}

[89] {{Title incomplete}}

[90] {{Year missing}}

[91] {{Dead link}}

[92] {{Contradict-inline}}

[93] {{Contradiction-inline}}

[94] {{Dubious|talk page section name}}

[95] {{Examples}}

[96] {{Inconsistent}}

[97] {{List fact}}

[98] {{Lopsided}}

[99] {{POV-statement}}

[100] {{Clarify timeframe}}

[101] {{Quantify}}

[102] {{Update after}}

[103] {{Update-small}}

[104] {{When}}

[105] {{Where}}

[106] {{Year needed}}

[107] {{Disambiguation needed}}

[108] {{Pronunciation needed}}

[109] {{Ambiguous}}

[110] {{Awkward}}

[111] {{Buzz}}

[112] {{Clarify}}

[113] {{Clarify span}}

[114] {{Definition}}

[115] {{Elucidate}}

[116] {{Expand acronym}}

[117] {{Technical-statement}}

[118] {{Vague|optional message to be displayed on mouseover}}

[119] {{Why?}}

[8] Foote, Jonathan (30 October 1999). Visualizing music and audio using self-similarity. pp. 77–80. doi:10.1145/319463.319472. ISBN 978-1581131512. http://musicweb.ucsd.edu/~sdubnov/CATbox/Reader/p77-foote.pdf.

[9] Pareyon, Gabriel (April 2011). On Musical Self-Similarity: Intersemiosis as Synecdoche and Analogy. International Semiotics Institute at Imatra; Semiotic Society of Finland. p. 240. ISBN 978-952-5431-32-2. Archived from the original on 8 February 2017. https://web.archive.org/web/20170208034152/https://tuhat.helsinki.fi/portal/files/15216101/Pareyon_Dissertation.pdf. Retrieved 30 July 2018. (Also see Google Books)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

自相似