自催化

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
Renhangqi（讨论 | 贡献）2022年5月23日 (一) 18:09的版本
跳到导航 跳到搜索


一个单一的化学反应，如果其中一个反应产物也是同一反应或耦合反应的催化剂，则称为具有自催化性质。[1]这种反应称为自催化反应 autocatalytic reaction。


如果一系列化学反应作为反应产物产生足够多的其他反应的催化剂，使整套化学反应在能量和食物分子输入的情况下能够自我维持，则可以说这些化学反应是”集体自催化”的。


化学反应

两种反应物和两种产物的化学反应可以写成

[math]\displaystyle{ \alpha A + \beta B \rightleftharpoons \sigma S + \tau T }[/math]


其中希腊字母是化学计量系数，大写拉丁字母代表化学物种。化学反应在正向和反向两个方向进行。这个方程可以很容易地推广到任意数量的反应物、产物和反应。


化学平衡

在化学平衡状态，正向和反向的反应速率是这样的情况：每一种化学物质都以同样的速率生成和消失。换句话说，正向反应的速率等于反向反应的速率。

[math]\displaystyle{ k_+ [ A ]^\alpha [B ]^\beta = k_{-} [S ]^\sigma[T ]^\tau \, }[/math]


这里，括号表示化学物质的浓度，以摩尔/升为单位，k+和k−是速率常数。


远离平衡态

在远离平衡态时，正向和反向反应速率不再是平衡的，反应物和产物的浓度不再是恒定的。对于每一个前向反应，[math]\displaystyle{ \alpha }[/math]的分子会消失。对于每一个逆反应，[math]\displaystyle{ \alpha }[/math]的分子都会被产生出来。在基本反应步骤中，每个方向的反应级数等于“反应分子数”，因此[math]\displaystyle{ \alpha }[/math]的摩尔数的变化率就是

[math]\displaystyle{ {d \over dt}[ A ] =-\alpha k_+ [ A ]^\alpha [B ]^\beta +\alpha k_{-} [S ]^\sigma[T ]^\tau \, }[/math]
[math]\displaystyle{ {d \over dt}[ B ] =-\beta k_+ [ A ]^\alpha [B ]^\beta +\beta k_{-} [S ]^\sigma[T ]^\tau \, }[/math]
[math]\displaystyle{ {d \over dt}[ S ] =\sigma k_+ [ A ]^\alpha [B ]^\beta -\sigma k_{-} [S ]^\sigma[T ]^\tau \, }[/math]
[math]\displaystyle{ {d \over dt}[ T ] =\tau k_+ [ A ]^\alpha [B ]^\beta -\tau k_{-} [S ]^\sigma[T ]^\tau \, }[/math]


这个系统的方程组有一个单一的稳定不动点解，这个解的情况就是每个物种的正向速率和反向速率相等（当每个物种[math]\displaystyle{ {d \over dt}=0 }[/math]）。这意味着这个系统是往平衡状态演化，而且这个平衡状态这是系统演化到的唯一状态。[2]


自催化反应

自催化反应中产物浓度的 s 形变化

自催化反应是那些其中至少一个产物是反应物的反应。最简单的自催化反应可以是这样的形式

[math]\displaystyle{ A + B \rightleftharpoons 2B }[/math]
[math]\displaystyle{ {d \over dt}[ A ] =- k_+ [ A ] [B ] + k_{-} [B ]^2 \, }[/math]
[math]\displaystyle{ {d \over dt}[ B ] = + k_+ [ A ] [B ] -k_{-} [B ]^2 \, }[/math].


使用速率方程（对于基本反应）

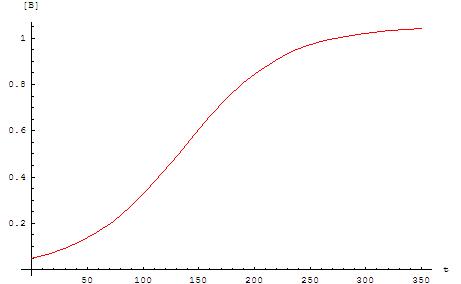
[math]\displaystyle{ [A]=\frac{[A]_0+[B]_0}{1+\frac{[B]_0}{[A]_0}e^{([A]_0+[B]_0)kt}} }[/math]
[math]\displaystyle{ [B]=\frac{[A]_0+[B]_0}{1+\frac{[A]_0}{[B]_0}e^{-([A]_0+[B]_0)kt}} }[/math].


这些方程的曲线图是一条s形曲线（特别是logistic函数），这是自催化反应的典型特征：这些化学反应在开始时（诱导期）进行得很慢，因为几乎没有催化剂存在，随着催化剂用量的增加，反应速度逐渐增加，然后随着反应物浓度的降低，反应速度再次减慢。如果一个实验中反应物或产物的浓度服从s形曲线，则该反应可能是自催化的 。


这些动力学方程适用于一些酯的酸催化水解为羧酸和醇。在飓风的例子中，飓风是由大气中不均匀的加热形成的。地球的大气层离热平衡还很远。地球大气的秩序增加了，但以太阳的秩序为代价。随着年龄的增长，太阳正变得越来越无序，并向宇宙的其他部分发射光和物质。尽管有秩序的飓风随时都会发生，但太阳和地球的整体混乱程度却在增加 。


秩序创立

背景

[[热力学第二定律]指出，物理或化学系统及其周围环境（封闭系统）的无序度（熵）必须随时间而增加。留给自己的系统变得越来越随机，系统的有序能量（如均匀运动）最终退化为粒子在[[热浴]中的随机运动


然而，在许多情况下，物理系统自发地变得新生或有序。例如，尽管飓风造成了破坏，但与封闭房间中空气分子的随机运动相比，飓风的运动非常有序。更引人注目的是化学系统创造的秩序；最引人注目的是与生命相关的秩序。


这与第二定律是一致的，第二定律要求系统“及其周围环境”的整体无序程度必须随时间而增加。在一个系统中，秩序可以通过系统周围环境的更大程度的降低而产生 [3] 在飓风的例子中，飓风是由大气中不均匀的加热形成的。地球的大气层离热平衡很远。地球大气的秩序增加了，但以太阳的秩序为代价。随着年龄的增长，太阳正变得越来越无序，并向宇宙的其他部分发射光和物质。尽管地球上产生了有序的飓风，但太阳和地球的总体混乱程度却在增加。


生命化学系统也有类似的例子。太阳为绿色植物提供能量。绿色植物是其他生物化学系统的食物。被植物吸收并转化为化学能的能量在地球上产生了一个有序的、远离[化学平衡]的系统。在这里，与化学平衡的差异是由反应物超过平衡量所决定的。地球上的秩序再一次以太阳的熵增加为代价。地球和宇宙其他部分的总熵增加，符合第二定律。


一些自催化反应也以牺牲周围环境为代价在系统中产生秩序。例如，（时钟反应）有中间体，其浓度随时间振荡，与时间顺序相对应。其他反应产生空间分离化学物种对应的空间顺序。在生物系统中的代谢途径和代谢网络涉及更复杂的反应


随着与平衡的距离增加，向有序的转变通常不是连续的。顺序通常会突然出现。化学平衡与有序之间的界限称为相变。相变的条件可以用非平衡态热力学的数学机制来确定


时间顺序

一个化学反应不能围绕最终的平衡的位置振荡，因为热力学第二定律要求热力学系统接近平衡，而不是从中退却。对于一个恒温恒压的封闭系统，Gibbs自由能必须连续下降而不振荡。然而，一些反应中间体的浓度可能会振荡，产物形成的“速率”也会振荡。[4]


理想化例子：Lotka–Volterra 等式

另一个演示时间顺序的系统例子是 Brusselator (见 Prigogine 参考文献)。人们的反应是拥有属性的

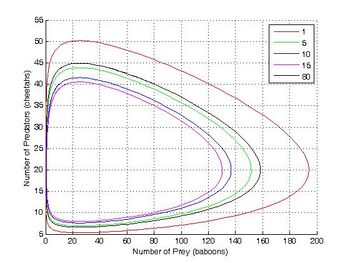
Lotka–Volterra方程式与捕食者-猎物模型和双反应自催化模型同构在这个例子中，狒狒和猎豹在自动催化反应中相当于两种不同的化学物种X和Y。


考虑一组耦合的两个自催化反应，其中一个反应物A的浓度远远大于其平衡值。在这种情况下，正向反应速率比反向速率大得多，我们可以忽略反向速率。

[math]\displaystyle{ A + X \rightarrow 2X }[/math]
[math]\displaystyle{ X + Y \rightarrow 2Y }[/math]
[math]\displaystyle{ Y \rightarrow E }[/math]


用速率方程

[math]\displaystyle{ {d \over dt}[ X ] = k_1 [ A ] [X ] - k_{2} [X ][Y ] \, }[/math]
[math]\displaystyle{ {d \over dt}[ Y ] = k_2 [ X ] [Y ] - k_{3} [Y ] \, }[/math].


这里，我们忽略了反应物A的消耗，因为它的浓度很大。这三个反应的速率常数是

[math]\displaystyle{ k_1 }[/math], [math]\displaystyle{ k_2 }[/math], and [math]\displaystyle{ k_3 }[/math].


这个速率方程组被称为Lotka–Volterra方程式，在捕食者-食饵关系中与族群动态最密切相关。这个方程组可以产生反应中间体 X 和 Y 的振荡浓度。振荡的振幅取决于 A 的浓度(A 的浓度下降而没有振荡)。这种振荡是一种涌现的时间顺序，在平衡中不存在。


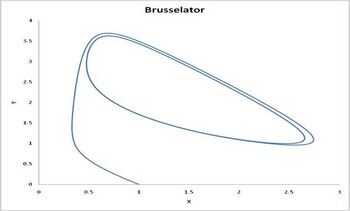
另一个理想化模型：布鲁塞尔振子

另一个演示时间顺序的系统示例是Brusselator(参见Prigogine参考)。它的特征是反应.

[math]\displaystyle{ A \rightarrow X }[/math]
[math]\displaystyle{ 2X + Y \rightarrow 3X }[/math]
[math]\displaystyle{ B + X \rightarrow Y + D }[/math]
[math]\displaystyle{ X \rightarrow E }[/math]

速率方程

[math]\displaystyle{ {d \over dt}[ X ] = [A ] + [ X ]^2 [Y ] - [B ] [X ] - [X ] \, }[/math]
[math]\displaystyle{ {d \over dt}[ Y ] = [B ] [X ] - [ X ]^2 [Y ] \, }[/math]


其中，为了方便起见，速率常数被设置为1。


不稳定政权中的布鲁塞尔人。A=1。B=2.5。X(0)=1。Y(0)=0。系统接近极限循环。对于 B<1+A，系统是稳定的并接近一个固定点。


布鲁塞尔振子有一个固定点在

[math]\displaystyle{ [ X ] = A \, }[/math]
[math]\displaystyle{ [ Y ] = {B \over A} \, }[/math].


固定点变得不稳定当

[math]\displaystyle{ B\gt 1+A^2 \, }[/math]

导致系统振荡。与 Lotka-Volterra 方程不同，Brusselator 的振荡不取决于最初存在的反应物的量。相反，在足够的时间之后，振荡接近极限循环。[5]


空间秩序

空间自发对称破缺的一个理想例子是这样的，我们有两个盒子的材料被一个透膜隔开，这样材料就可以在两个盒子之间扩散。假设每个盒中都有相同的布鲁塞尔子，且初始条件几乎相同。(见Prigogine参考)

[math]\displaystyle{ {d \over dt}[ X_1 ] = [A ] + [ X _1]^2 [Y_1 ] - [B ] [X_1 ] - [X_1 ] + D_x\left( X_2 - X_1 \right)\, }[/math]
[math]\displaystyle{ {d \over dt}[ Y_1 ] = [B ] [X_1 ] - [ X_1 ]^2 [Y_1 ] + D_y\left( Y_2 - Y_1\right) \, }[/math]
[math]\displaystyle{ {d \over dt}[ X_2 ] = [A ] + [ X _2]^2 [Y_2 ] - [B ] [X_2 ] - [X_2 ] + D_x\left( X_1 - X_2 \right)\, }[/math]
[math]\displaystyle{ {d \over dt}[ Y_2 ] = [B ] [X_2 ] - [ X_2 ]^2 [Y_2 ] + D_y\left( Y_1 - Y_2\right) \, }[/math]

在这里，数字下标表示材料在哪个盒子里。还有一些与扩散系数D成比例的附加项，它们解释了盒子之间的物质交换。


如果系统在每个箱子的相同条件下启动，那么小的波动将导致两个箱子之间的物料分离。一个方框的优势是X，另一个方框的优势是Y。


实例

时钟反应的真实例子是Belousov–Zhabotinsky反应（B-Z反应）、Briggs–Rauscher 反应、Bray–Liebhafsky 反应和碘钟反应。这些都是振荡反应，产物和反应物的浓度可以用阻尼，振荡来近似


其中最著名的反应是B-Z反应，可以用溴酸钾的混合物产生[math]\ce{ (KBrO3) }[/math], 丙二酸[math]\ce{ (CH2(COOH)2) }[/math], 和硫酸锰[math]\ce{ (MnSO4) }[/math]在加热的硫酸溶液中制备[math]\ce{ (H2SO4) }[/math]作为溶剂。[6]


光学实例

另一种自催化系统是由光耦合到光聚合反应驱动的。在一个称为光自催化的过程中，通过聚合引起的折射率增加，光强度和光聚合速率之间产生了正反馈。光倾向于占据高折射率区域，从而导致光泄漏到高分子量区域，从而放大了光化学反应。正反馈可以表示为:[7]

[math]\displaystyle{ \text{polymerization rate} \to \text{molecular weight}/\text{refractive index} \to \text{intensity} }[/math]

聚合速率→分子量/折射率→强度


注意到光聚合速率与强度成正比，[8]折射率与分子量成正比，[9]强度和光聚合之间的正反馈建立了自催化行为。光自催化已经被证明可以导致光聚合物中自发图案的形成。[10][11][12]Hosein和他的同事发现，光自催化也可以发生在光活性聚合物混合物中，并且该过程可以诱导具有与光轮廓相同图案的二元相形态。[7] 光经历了光调制不稳定性，自发地分裂成许多光学细丝，因此，聚合物系统在共混结构中形成细丝。[7] 结果是一个将光学自催化行为与旋节分解相耦合的新系统。


生物实例

众所周知，一个重要的代谢循环，即糖酵解，显示出时间顺序。[13] 糖酵解包括一个葡萄糖分子的降解和两个分子 ATP的合成。因此，这个过程对活细胞的能量学非常重要。全局糖酵解反应涉及葡萄糖、 ADP、 NAD、丙酮酸、 ATP 和 NADH。

[math]\ce{ glucose{} + 2ADP{} + 2P_\mathit{i}{} + 2NAD -> 2(pyruvate){} + 2ATP{} + 2NADH }[/math].


过程的细节是相当复杂的，然而，过程的一部分是由磷酸果糖激酶（PFK）自动催化的。这个过程的这一部分负责路径中的振荡，导致过程在一个活跃的和一个不活跃的形式之间振荡。因此，自催化反应可以调节这一过程。


薄层剪裁

可以使用自催化反应的结果与反应-扩散系统理论相结合来定制薄层的设计。自催化过程允许控制氧化前沿的非线性行为，该行为用于建立生成任意最终几何形状所需的初始几何形状。[[14]已在湿法氧化中成功完成[math]\displaystyle{ Al_xGa_{1-x}As }[/math]获得任意形状的层[math]\displaystyle{ AlO_x }[/math]。


相变

反应物的初始量决定了与体系化学平衡的距离。初始浓度越大，系统离平衡越远。随着初始浓度的增加，阶发生突变。这种突变被称为相变。在相变阶段，宏观量的波动，如化学浓度，随着系统在更有序的状态（低熵，如冰）和更无序的状态（更高的熵，如液态水）之间振荡而增加。同样，在相变过程中，宏观方程，如速率方程，会失效。速率方程可以从微观角度推导出来。推导通常依赖于对微观动力学方程的平均场理论近似。平均场理论在大波动的情况下会崩溃（见平均场理论文章进行讨论）。因此，由于大的波动发生在相变附近，宏观方程，如速率方程，失败了。随着初始浓度的进一步增加，系统进入有序状态，在这种状态下波动又很小。（见Prigogine参考文献）


不对称自催化

非对称自催化发生在反应产物为手性时，因此作为手性催化剂进行自身生产。这种类型的反应，如Soai反应，具有将很小的对映体过量放大为大反应的性质。这被认为是生物学纯手性起源的重要一步。 [15]


生命起源中的角色

1995 年斯图尔特·艾伦·考夫曼 Stuart Alan Kauffman提出生命最初是作为自催化化学网络出现的。[16]


英国 动物行为学家理查德·道金斯 Richard Dawkins在他 2004 年出版的《祖先的故事 The Ancestor's Tale》一书中将自催化作为对非生物发生的潜在解释。他引用了加利福尼亚斯克里普斯研究所的 Julius Rebek 和他的同事进行的实验，他们将氨基腺苷和五氟苯酯与自催化剂氨基腺苷三酸酯 (AATE) 结合在一起。实验中的一个系统包含催化自身合成的 AATE 变体。该实验证明了自动催化剂可能在具有遗传的实体群体中表现出竞争的可能性，这可以解释为一种基本形式自然选择，并且某些环境变化（例如辐照）可能会改变其中一些自我复制分子（突变的类似物）的化学结构，从而增强或干扰其反应能力，从而增强或干扰其反应能力。干扰其在人群中复制和传播的能力。[17]


自催化在生命过程中发挥着重要作用。两位强调其在生命起源中的作用的研究人员是 Robert Ulanowicz [18]和 Stuart Kauffman。[19]


自催化发生在 rRNA 的初始转录物中。内含子能够通过两个亲核酯交换反应的过程自我切除。能够做到这一点的 RNA 有时被称为核酶。此外，柠檬酸循环是反向运行的自催化循环。


最终，生物代谢本身可以被视为一个巨大的自催化集合，因为生物细胞的所有分子成分都是由涉及同一组分子的反应产生的。


另见


参考文献

  1. ↑ Steinfeld J.I., Francisco J.S. and Hase W.L. Chemical Kinetics and Dynamics (2nd ed., Prentice-Hall 1999) p.151-2.
  2. ↑ Ross, John; Garcia-Colin, Leopoldo S. (March 1989). "Thermodynamics of chemical systems far from equilibrium". The Journal of Physical Chemistry. 93 (5): 2091–2092. doi:10.1021/j100342a075.
  3. ↑ Ilya Prigogine (1980). From Being to Becoming: Time and Complexity in the Physical Sciences. San Francisco: W. H. Freeman. ISBN 978-0-7167-1107-0. https://archive.org/details/frombeingtobecom00ipri. 
  4. ↑ Espenson, J.H. Chemical Kinetics and Reaction Mechanisms (2nd ed., McGraw-Hill 2002) p.190.
  5. ↑ "Archived copy" (PDF). Archived from the original (PDF) on 2008-12-17. Retrieved 2015-10-15.{{cite web}}: CS1 maint: archived copy as title (link) Dynamics of the Brusselator
  6. ↑ Peterson, Gabriel. "The Belousov-Zhabotinsky Reaction". Archived from the original on December 31, 2012.
  7. ↑ 7.0 7.1 7.2 Biria, Saeid; Malley, Phillip P. A.; Kahan, Tara F.; Hosein, Ian D. (2016-11-15). "Optical Autocatalysis Establishes Novel Spatial Dynamics in Phase Separation of Polymer Blends during Photocuring". ACS Macro Letters. 5 (11): 1237–1241. doi:10.1021/acsmacrolett.6b00659.
  8. ↑ Decker, Christian (1998-02-01). "The use of UV irradiation in polymerization". Polymer International (in English). 45 (2): 133–141. doi:10.1002/(SICI)1097-0126(199802)45:2<133::AID-PI969>3.0.CO;2-F.
  9. ↑ Askadskii, A. A. (1990). "Influence of crosslinking density on the properties of polymer networks". Polymer Science U.S.S.R. 32 (10): 2061–2069. doi:10.1016/0032-3950(90)90361-9.
  10. ↑ Burgess, Ian B.; Shimmell, Whitney E.; Saravanamuttu, Kalaichelvi (2007-04-01). "Spontaneous Pattern Formation Due to Modulation Instability of Incoherent White Light in a Photopolymerizable Medium". Journal of the American Chemical Society. 129 (15): 4738–4746. doi:10.1021/ja068967b. ISSN 0002-7863. PMID 17378567.
  11. ↑ Basker, Dinesh K.; Brook, Michael A.; Saravanamuttu, Kalaichelvi (2015). "Spontaneous Emergence of Nonlinear Light Waves and Self-Inscribed Waveguide Microstructure during the Cationic Polymerization of Epoxides". The Journal of Physical Chemistry C (in English). 119 (35): 20606–20617. doi:10.1021/acs.jpcc.5b07117.
  12. ↑ Biria, Saeid; Malley, Philip P. A.; Kahan, Tara F.; Hosein, Ian D. (2016-03-03). "Tunable Nonlinear Optical Pattern Formation and Microstructure in Cross-Linking Acrylate Systems during Free-Radical Polymerization". The Journal of Physical Chemistry C. 120 (8): 4517–4528. doi:10.1021/acs.jpcc.5b11377. ISSN 1932-7447.
  13. ↑ G. Nicolis and Ilya Prigogine (1977). Self-Organization in Nonequilibrium Systems. New York: John Wiley and Sons. ISBN 978-0-471-02401-9. 
  14. ↑ Alfaro-Bittner, K.; Rojas, R.G.; Lafleur, G.; Calvez, S.; Almuneau, G.; Clerc, M.G.; Barbay, S. (22 April 2019). "Modeling the Lateral Wet Oxidation of into Arbitrary Mesa Geometries". Physical Review Applied. 11 (4): 044067. doi:10.1103/PhysRevApplied.11.044067.
  15. ↑ Soai K, Sato I, Shibata T (2001). "Asymmetric autocatalysis and the origin of chiral homogeneity in organic compounds". The Chemical Record. 1 (4): 321–32. doi:10.1002/tcr.1017. PMID 11893072.
  16. ↑ Stuart Kauffman (1995). At Home in the Universe: The Search for the Laws of Self-Organization and Complexity. Oxford University Press. ISBN 978-0-19-509599-9. https://archive.org/details/athomeinuniverse00kauf_0. 
  17. ↑ Rebeck, Julius (July 1994). "Synthetic Self-Replicating Molecules". Scientific American: 48–55.
  18. ↑ Ecology, the Ascendent Perspective", Robert Ulanowicz, Columbia Univ. Press 1997.
  19. ↑ Investigations, Stuart Kauffman.


编辑推荐

集智课程

生命起源的最重要的问题——主体性与层级跃迁

生命作为最典型的复杂系统，从细胞到个体再到群体，在不同层次上都展现出各种复杂性，引发不同学科研究者的兴趣。为了促进生命复杂系统的跨学科交流，我们策划“生命复杂性”系列读书会，组织精读和讨论相关研究。生命起源是最迷人的科学问题之一，也是生物、化学、地质等多个学科的汇合地。而从复杂性科学的视角看，生命起源和发展是一个多次涌现、逐层跃迁的过程。

该课程中介绍了关于生命起源的四大经典理论和最新工作，并讨论生命分阶段起源的定量研究设想。


生命起源与自我复制

该课程介绍了生命起源与自我复制的概念以及其它们之间的关系。


本中文词条由Henry翻译，柯里昂审校，薄荷编辑，如有问题，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=自催化&oldid=31407”