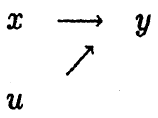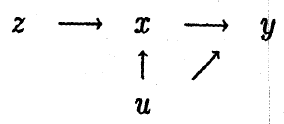工具变量
工具变量是指与处理直接相关、与混杂变量独立并且与结局没有直接因果关系的变量。工具变量方法是在观察性研究中估计因果作用的一种常用方法。
工具变量是与do演算不同的联系干预层和观测层的一种方法,它通过在观测层模拟随机控制试验来得到干预层的信息,从而实现因果效应估计,它在计量经济学、流行病学中被普遍应用。尽管do演算能够计算出所有可识别的因果效应,但是对于不可识别的情况,do演算无法把干预层表达式变形为观测层表达式。此时,如果满足一定条件,工具变量也许可以发挥作用[1][2]。
"它能帮助我们揭示do演算无法揭示的因果信息"。[3]——Judea Pearl
"虽然关于工具变量集的识别问题超越了do演算的应用范畴,但我们仍然可以借助因果图来解决这个问题"。[3]——Judea Pearl
工具变量概念
工具变量假定
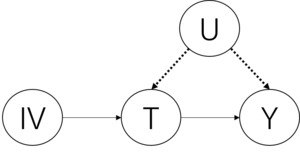
如图所示,当我们在研究干预变量(治疗变量)对于结果变量的影响时,如果干预变量和结果变量存在不可观测的共同原因,那么干预变量对于结果变量的因果效应是不可识别的。此时,可以通过随机对照实验去混杂,可以引入干预变量和结果变量之间可观测的中介变量去混杂,当满足下列条件时,也可以通过其他变量(工具变量)去混杂:
假设1:相关性(Relevance)
存在工具变量指向干预变量的因果箭头
假设2:排除限制(Exclusion Restriction)
工具变量对于结果变量的因果效应完全以治疗变量为中介
假设3:工具变量无混杂(Instrumental Unconfoundedness)
工具变量与混杂因子之间不存在因果箭头
通常还会有因果机制线性或单调性假设。
应用案例
1853-1854年,英格兰爆发了霍乱疫情。霍乱是一种由霍乱细菌引起,主要通过水源传播的疾病,但是当时,人们此一无所知,一种具有竞争力的观点认为霍乱是由某种不可观测的“瘴气”引起该疾病,而且“瘴气”会污染水源。John Snow研究的是水源对于霍乱的影响,“瘴气”是混杂因子,供水公司是工具变量,但他并非有意识的使用工具变量。
1928年,遗传学家Sewall Green Wright的父亲经济学家Philippe Wright写的论文讨论亚麻籽油供给的弹性问题,即研究供应对价格的影响和价格对供应的影响,需求是混淆因子,他引入了亚麻籽每英亩的可变产量作为工具变量。
在临床试验的未履行问题(noncompliance)中,消胆胺服用是干预变量,胆固醇水平是结果变量,药物分配是工具变量,混杂因子可能是身体状况等。
孟德尔随机化是工具变量的另一种衍生版本。
IV 估计法的基本思想
从一个最简单的回归模型引入工具变量估计法。如下式(1)所示:
y = βx+u(1)
假设y度量的是收入, x度量的是受教育的年数, u为随机误差项。简单回归模型(1)假设 x与随机误差项u不相关。x 对y的唯一直接影响是通过βx带来的,如下图(1)所示:
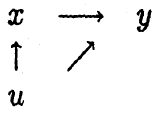
随机误差项u包括了除受教育年数之外的所有其他未观测到的影响收入的因素,能力 的因素包括在 u 中,因为 能力 的高低与 收入 (y) 具有相关性(一般的,能力高的人收入会高)。但同时 能力 的高低与 受教育年数 (x) 也具有相关性(一般的,能力高的人倾向于接受更多的教育或技能培训),如下图(2)所示:
在模型(1)中我们遗漏了 能力 这个重要变量,在这种情况下,OLS 估计量β<~>就不是β的一致估计量,因为β<~>包括了两部分的影响效果:一部分 是我们期望得到的受教育年数对收入的直接影响,另一部分 是来自于能力的间接影响,例如,能力高的人通常会有较高的受教育年数,从而有较高的收入。如果受教育时间增加 1 年与年收入增加 1,000 美元相关,我们就不能确定增加的 1,000 美元当中有多少是来自于 受教育年数多的影响,有多少是来自于 能力高 的影响。
我们可以使用工具变量估计法解决上述内生性问题。引入一个新的工具变量z ,它具有以下性质:z的变化与x的变化相关;除了 z会间接的通过影响 x来影响 y之外,z 的变化不会导致y 的变化。例如,与大学相邻 (z) 可能会决定是否上大学,从而影响受教育年数 (x),但并不直接决定收入 (y)。如下图3所示:
当 x的工具变量 z满足以下条件时,IV 估计量 β<^>_iv是一致估计量: (1)z 与 x 相关; (2)z 与 u 不相关。
IV 估计式
在一般形式的回归模型(2)中(以矩阵形式表示):
y = Xβ+u
X是由解释变量构成的 N×k 维矩阵, β是系数向量。定义一个矩阵 Z(z_1,z_2,....z_k)与X(x_1,x_2,....x_k) 有着相同的维度,作为X的工具变量,将(2)式两端同乘以矩阵Z' ,则有:
Z'y = Z'Xβ+Z'u
工具变量 Z与u 不相关,意味着当 N趋于无穷大时 1/N(Z'u) 的概率极限为 0。因此,我们可以从下式中定义出 IV 估计量β<^>_iv :
Z'y = Z'Xβ<^>_iv
β<^>_iv = (Z'X)^(-1)Z'y
IV 估计量的一种有趣的情况是:如果零条件均值假设满足,每一个解释变量都可以做为自己的工具变量,即 X=Z,此时,IV 估计量就缩减为 OLS 估计量。因此,当零条件均值假设满足时,OLS 估计量是 IV 估计量的一种特殊情形。
代码实现
DAGitty:www.dagitty.net/dags.html
BayesiaLab:www.bayesia.com
参考文献
- ↑ https://cosx.org/2013/08/causality6-instrumental-variable
- ↑ 苗旺,刘春辰,耿直 (2018) 因果作用与因果网络. 中国科学-数学, 48, 1753-1778.
- ↑ 3.0 3.1 Pearl, Judea, and Dana Mackenzie. The book of why: the new science of cause and effect. Basic books, 2018.
编辑推荐
课程推荐
这个视频内容来自集智俱乐部读书会-因果科学与Causal AI读书会第三季内容的分享,本次读书会邀请到浙江大学况琨老师、吴安鹏和袁俊坤两位博士生从工具变量的视角,介绍如何利用机器学习赋能大数据因果推断。报告将从因果推断的工具变量视角出发,探讨领域泛化问题中存在的偏差问题,并提出因果可泛化学习机制。
第一部分将从解耦表征学习的角度出发,将观察性研究中涉及的协变量区分为工具变量、混淆变量、调整变量三部分。报告将探讨在非混淆性假设不成立时,如何从观察性数据中基于一定先验假设进行简单工具变量识别的方法。最后我们给出了一种结合混淆平衡方法和工具变量方法的最新研究,能够同时消除观察到的混淆变量和观察不到的隐变量带来的混淆偏倚。
第二部分将从因果的角度探讨领域泛化问题,引入工具变量的思路解决领域泛化中关键性的域不变关系学习问题,从多个源域中学习出稳定的因果关系,提升模型在未知数据域上的泛化表现。
相关路径
- 因果科学与Casual AI读书会必读参考文献列表,这个是根据读书会中解读的论文,做的一个分类和筛选,方便大家梳理整个框架和内容。
- 因果推断方法概述,这个路径对因果在哲学方面的探讨,以及因果在机器学习方面应用的分析。
- 因果科学和 Causal AI入门路径,这条路径解释了因果科学是什么以及它的发展脉络。此路径将分为三个部分进行展开,第一部分是因果科学的基本定义及其哲学基础,第二部分是统计领域中的因果推断,第三个部分是机器学习中的因果(Causal AI)。