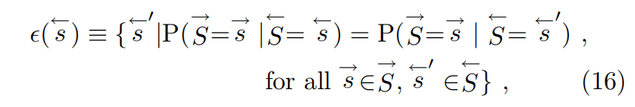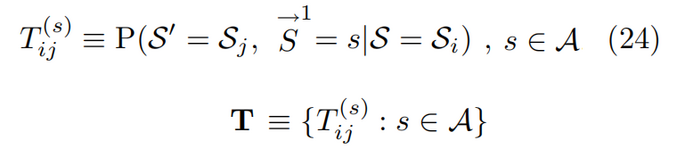计算力学
摘要
计算力学是一种方法，用来结构化复杂性，定义一个过程的因果态，并给出一个找出它们的步骤。我们展示了因果态的表示-一个ε机制-拥有最小复杂度的同时又能拥有最准确预测能力。
圣塔菲研究所 99-07-044
目录
简介
有组织的物质在自然界中是广泛存在的，物理学的分支应该可以处理它-统计力学-只是缺乏一致性，原则性的方式去描述，测量，以及检测这么多自然展示出来的不同结构。
因果态定义
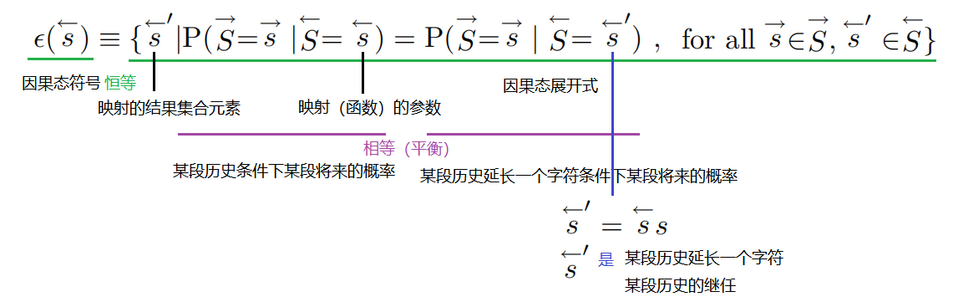
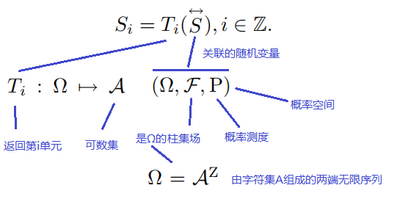
这是一个恒等式，左侧是符号，右集是幂集的内容，具体解析如下：
上述的因果态公式可以看成是这定义，我们也可以去可以根据这个定义，去寻找满足条件的s。条件就是两个概率要相等。
上式是因果态的定义，以及对这个定义式的一些简单的认识。我们可以认为是从随机过程
定义出因果态，花体的
代表第i个因果态，所有因果态用
来表示。
计算力学除了因果态ε外，还有另一半就是状态转移：
这个定义看上去不太直观，我们附上文字的内容
薛老师是读书会的主讲人，讨论了满足这个定义的存在性。因果态的一个理解是，给定一段历史，有一个对将来的预测，它后续历史也有一个对将来的预测，预测的两个概率要相等。个人理解存在性可能需要用更深层的理论证明。
这里只是因果态的定义，在因果态结合状态转移才形成“计算力学”的ε机制。
因果态和状态转移有序组构成了ε机制
也可以用所有因果态和转换表示
至此，我们完成了“计算力学”的主要定义。
我们一般将随机过程看成是线条状的，但不知为何在论文中它可以形成一个“面”，然后可以被划分成不同的“部分”。令人想到的是蛋白质的折叠，不知到这两者是否有关系。
从个人视角出发，历史是一天天形成的轨迹，有两点一线，也有新的突破。最初对能折叠历史的印象，会是一种分形结构：
这种绕曲的结构如何形成水池和做划分的呢？需要请教大家。文章中的“过程（Process）”是位于“整体（Ensemble）”空间的，所以这种最初印象可能不正确。
在文章中找到了原始的定义
Ω是AZ的无限序列，这里Z是A的上标，是表示幂集吗？如果是，Ω等于一个幂集，这其中发生了什么？让我们再回顾下这个过程，A加上标Z变成幂集，然后赋给Ω，Ω经过Ti的映射又变回A'，此A非彼A'？
期待大家的批评指正，谢谢！