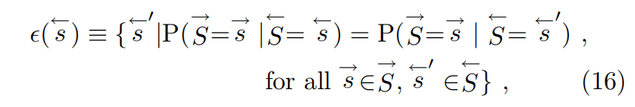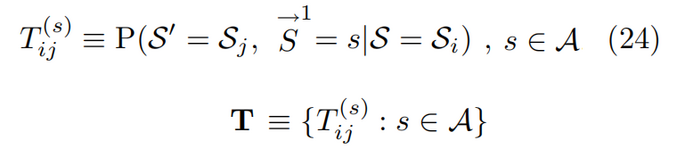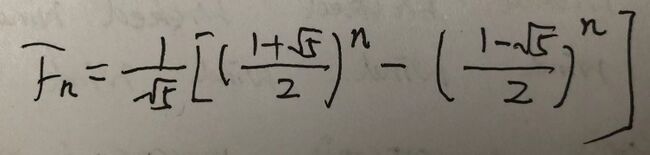计算力学

正文是对http://arxiv.org/abs/cond-mat/9907176v2文章的翻译

标题

计算力学：班图和预测，结构和简化

Cosma Rohilla Shalizi∗ 和 James P. Crutchfield

圣塔菲研究所，1399 Hyde 公园路，圣塔菲，NM 87501

电子邮箱地址：{shalizi,chaos}@santafe.edu

（2008年2月1日）

摘要

计算力学是一种方法，用来结构化复杂性，定义一个过程的因果态，并给出一个找出它们的步骤。我们展示了因果态的表示-一个ε机制-拥有最小复杂度的同时又能拥有最准确预测能力。我们在ε机制优化和识别上，以及如何将ε机制同其他表征相比较上，建立了几个结果。更多结果是关于测量从ε机制到一些遍历及信息理论获得的随机性和结构复杂度。

圣塔菲研究所研究论文 99-07-044

关键字：复杂性，计算，熵，信息，斑图，统计力学页眉：计算力学

简介

斑图

在奥卡姆水池周边填充

计算力学

优化和标识

极限

结论备注

附录

参考文献

名词术语

有组织的物质在自然界中是广泛存在的，物理学的分支应该可以处理它-统计力学-只是缺乏一致性，原则性的方式去描述，测量，以及检测这么多自然展示出来的不同结构。

以下是个人的一些整理

因果态和计算力学中存在大量的大S，小s，和花S等符号。对于有些人，这些符号理解起来有些困难，因为很多人一生就从事某几种职业，轨迹就那么多。或许形成了一个组织，才是一个大S，而个体就是小s了。花S可能就是互相促进的一些道路吧。

因果态定义

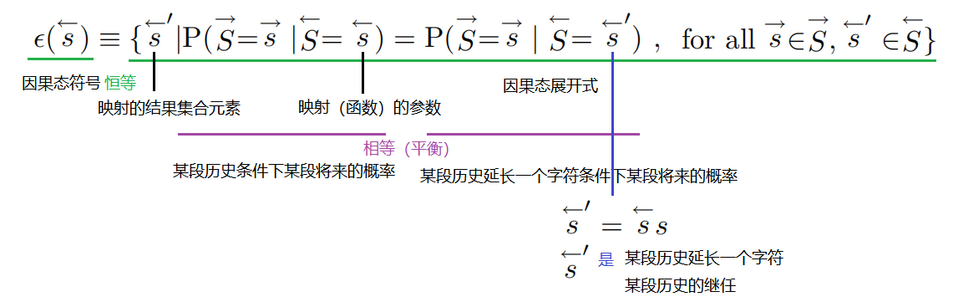
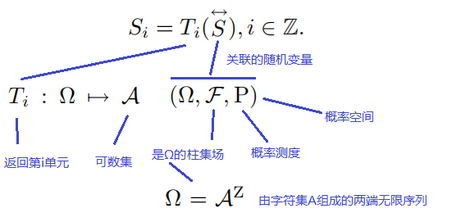
这是一个恒等式，左侧是符号，右集是幂集的内容，具体解析如下：

上述的因果态公式可以看成是这定义，我们也可以去可以根据这个定义，去寻找满足条件的s。条件就是两个概率要相等。

上式是因果态的定义，以及对这个定义式的一些简单的认识。我们可以认为是从随机过程定义出因果态，花体的代表第i个因果态，所有因果态用来表示。

计算力学除了因果态ε外，还有另一半就是状态转移：

这个定义看上去不太直观，我们附上文字的内容

薛老师是读书会的主讲人，讨论了满足这个定义的存在性。因果态的一个理解是，给定一段历史，有一个对将来的预测，它后续历史也有一个对将来的预测，预测的两个概率要相等。个人理解存在性可能需要用更深层的理论证明。

这里只是因果态的定义，在因果态结合状态转移才形成“计算力学”的ε机制。

因果态和状态转移有序组构成了ε机制

也可以用所有因果态和转换表示

至此，我们完成了“计算力学”的主要定义。

我们一般将随机过程看成是线条状的，但不知为何在论文中它可以形成一个“面”，然后可以被划分成不同的“部分”。令人想到的是蛋白质的折叠，不知到这两者是否有关系。

从个人视角出发，历史是一天天形成的轨迹，有两点一线，也有新的突破。最初对能折叠历史的印象，会是一种分形结构：

这种绕曲的结构如何形成水池和做划分的呢？需要请教大家。文章中的引文【90】和【91】有提到“来自时间序列的几何形状”，里面可能有相应的方法，引文【92】从数据序列估计最小动态等式，也有可能涉及。

文章中的“过程（Process）”是位于“整体（Ensemble）”空间的，所以这种最初印象可能不正确。

在文章中找到了原始的定义

Ω是A^Z的无限序列，这里Z是A的上标，是表示幂集吗？如果是，Ω等于一个幂集，这其中发生了什么？让我们再回顾下这个过程，A加上标Z变成幂集，然后赋给Ω，Ω经过Ti的映射又变回A'，此A非彼A'？

期待大家的批评指正，谢谢！

========

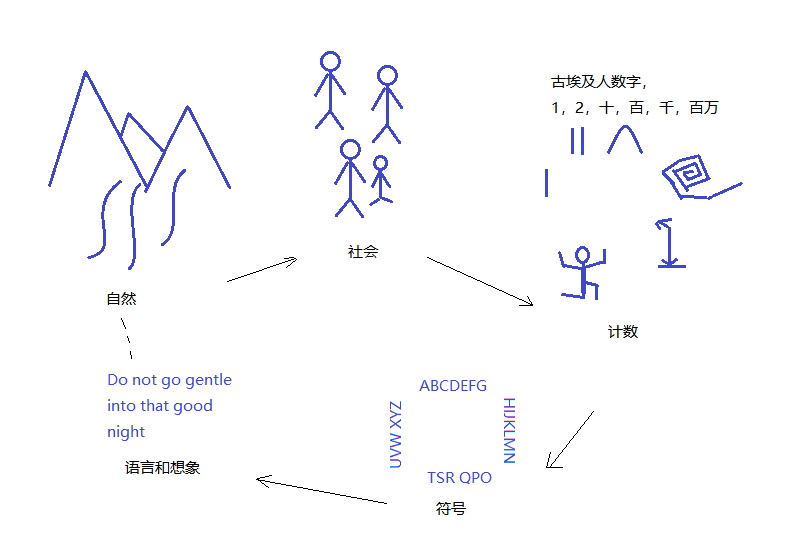
初看这篇文章，开头有对自然的描述，还是容易理解的，但到符号部分就很烧脑了。我们既然读到了这篇文章，还是想办法把其中的内容串起来，使用人们的生产生活的经验，结合自然规律就是一种串联的方式。我们从数字的发展史开始：

从社会的角度来看，符号的产生与发展，与自然及社会成员间的交互是密不可分的。这种与自然或成员的交互可以定义概念，而一个概念的记录形式有多种，呈现一种概率分布，经过交互后，可形成新的分布。这些不同的概念又可以有不同的结合，当时人们并不清楚这些结合的含义，最后的含义可以赋与，也可以涌现。

从读书会的文章，我们识别出社会到符号的一种可能是结构，这个结构中，自然到社会，属于生物学家的专业，社会到计数，属于历史学家的专业，符号到语言，有语言学家在专精这一块。我们只是在计数到符号这一过程做点耕耘。我们结合社会化大生产，来补充文章中的变换、零点，并结合实际案例，来打破传统的计算过程，迎接新的挑战。

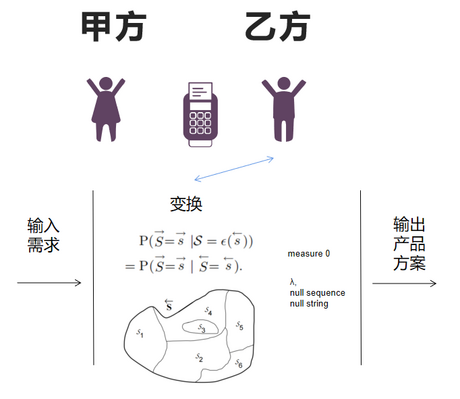
Morphs(变换)

天上不会掉馅饼！馅饼是由粮食做出来的，在制做过程中凝聚了大量的人类智慧和劳动。所以在一个由人类组成的特定类型组织中，变换无所不在。作为社会一员，希望大家都能掌握一种变换法则，在社会中占有一席之地。

零点

文章论述过程中有大量measure 0和λ, the null sequence.起码系统中是允许这样的元素存在的，这样元素的作用还需要进一步学习。

逆运算

传统的计算都是正向的，比如先有火车，再有座位。但也可以逆向，需要多少座位，再去找火车。我们可以去尽量满足需求，但也要尽量避免系统陷入不稳定。

难题与智能

在混沌课程中，有介绍种群增长模型，它是一个指数增长。每次采样，我们认为是一次迭代。将它写成微分方程

dN(t)/dt = rN(t)

这是没有考虑环境的压力下的，一个生态学假设。引入环境压力后，模型就呈现Logistic形式：

dN(t)/dt = rN(t)(1-N(t)/K)

如果将“1-N(t)/K”看作是抑制项，那是否可以从促进和抑制作用，来看待智能？地球迈入人类纪，怎么更好地理解“科技以人为本”？

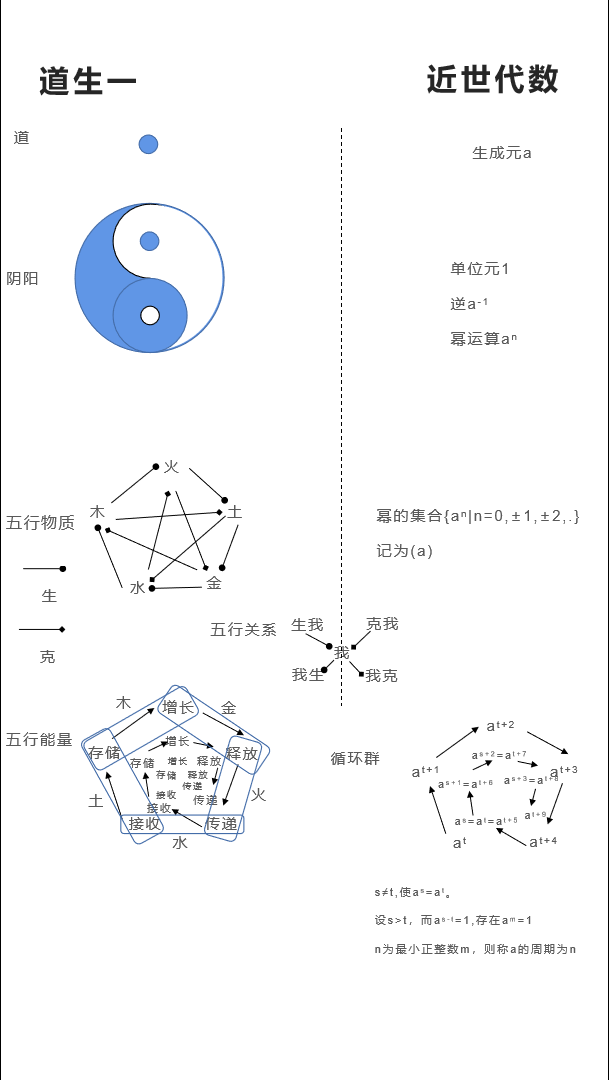
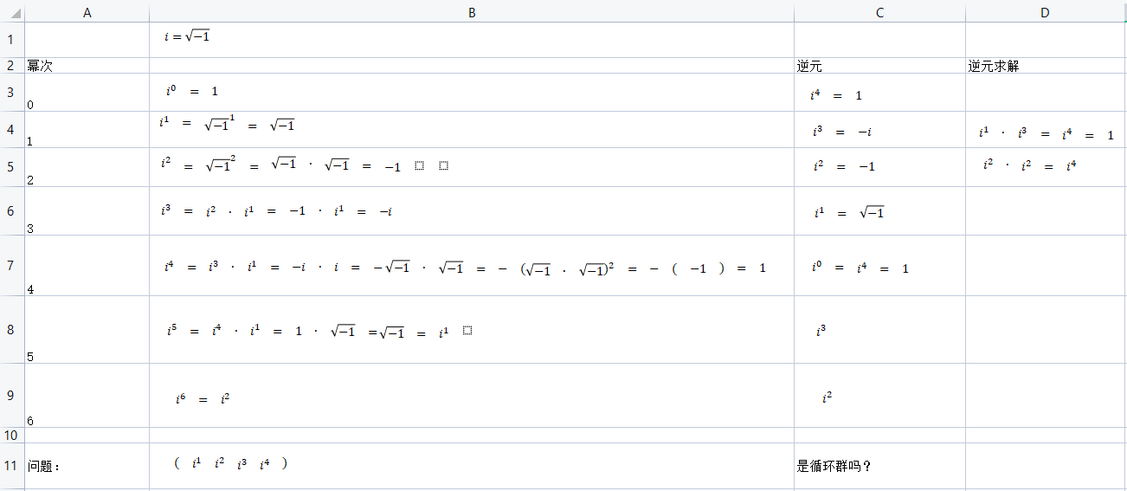
循环群

循环群是说，某系统发展到一定程度，会和历史上的阶段相似。数学上的定义是相等，但我们研究的系统，大部分是开放的。所以发展到一定阶段，跟历史接近就可以了。循环群不单用来研究历史，也可以用来研究时序数据，比如第一次工业革命，蒸汽机的齿轮曲轴连杆结构。如果你单看某根杆，是难以彻底理解轮杆结构的工作机制，如果试着把轮杆结构的一个大循环梳理出来，就容易理解了。“机器”大多数时候，是一个往复运动。把这个往复运动抽象成循环群，再辅以蒸汽机整体在“世界”中的运动，基本上能把握到脉络。

重新认识循环群，也是受阴阳五行的启发。有人把五行细化为能量的循环，但他没有把循环封闭，而是下次循环和上次接近，这样更容易使用分形和耗散结构去分析。我个人了解五行，也是想知道相生相克，毕竟就算是蒸汽机的齿轮曲轴连杆结构，也是A和B机构受到挤压，使得C机构以指定方式运动。人生就该多姿多彩，幸好集智上线了“混沌”的课程，所以大家可以想想，熟练工作，循环多次，下一次该多大程度接近起点？

最近看了一下循环群的定义和性质，大致是幂（同一运算迭代）运算到某个值，接近开始位置。循环群是一类被完全解决的群，虽然不知道是啥意思，但以地球和三体来类比，地球有生命，其实是它的轨道还算可以预测；而三体只是想象的过程，在其中寻找稳定结构或秩序，应该是有一定难度的。从计算力学的角度来看，完全优化的轨迹，就是决定论的范畴。地球的轨迹和生态，是完整的循环吗？

近世代数当中，从代数系统介绍到循环群时，逐步引入运算，直到幂（指数）。在现实的复杂系统中，更容易观测的运算可能是幂，因为时空是并发的。观测单个运算，才有加法和乘法。意思其实是，很多事物，成品是幂率，但你要理解它，却要从代数系统开始。这是数学语言，音乐有自己的语言，建筑也是。一般音乐有一个特点，由主音开始，随着旋律的进行，各音不断出现，最后结束时会回到主音，和循环群的特点很好的匹配。成品是台上的东西，你能看到幂率和分形，也就是台上的二分钟。但台下数年功，却不容易被看到，有前进，也有迂回。

在理解记忆近世代码的过程中，出现的一个分岔。循环群和元素的阶容易弄混，元素的阶是指该元素幂次n后等于单位元。i=根号-1。