复杂网络中的因果涌现

因果涌现理论最初是由Erick Hoel提出，使用有效信息来量化离散马尔可夫动力学的因果性强弱。2020 年，Klein 等人尝试将该方法应用于复杂网络中，然后为了量化复杂网络中的因果涌现，需要解决如下问题：定义网络中的动力学，定义有效信息，网络如何粗粒化等问题。

定义网络中的动力学

由于因果涌现理论量化的是系统的动力学，对于网络来说，需要定义网络节点的动力学，可以借助随机游走子定义网络中的马尔可夫链，从而假定网络中的每个节点具有随机游走动力学。

有效信息定义

将随机游走子放在节点上，等价于对节点做干预do(·) ，基于随机游走概率可以定义节点的转移概率矩阵，将网络节点类比系统状态构建网络动力学的有效信息；建立了有效信息与网络连通性的联系。网络中的连通性可通过节点出边与入边的权重的不确定性表征 2 项衡量：1）节点输出的不确定性可通过节点出权的香农熵定义，即 ，因此整个网络的不确定性可通过得到；2）基于网络的出边权重分布计算，反映了确定性如何在网络中分布. 通过这2项就可得到复杂网络中的有效信息定义。 进一步，有效信息可以分解为确定性和简并性。

网络中的粗粒化

为了识别复杂网络中的因果涌现，需要对网络进行粗粒化，然后比较宏观网络与微观网络的有效信息，判断能否发生因果涌现。粗粒化方法包括：贪婪算法、谱分解方法以及机器学习方法。

机器学习方法

困难： 1. 初始化分组矩阵的选择，多次重复实验会得到不一样的结果 2. 依赖神经网络的超参，如学习率、迭代次数等

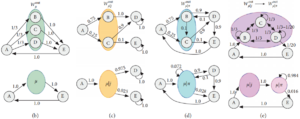
通过对节点进行分组，并构建宏观网络。将微观节点合并成宏观节点时，对应宏观网络的转移概率矩阵也要进行相应的处理. 通过使用高阶节点显式地对高阶依赖项建模（HOMs），保证分组后的宏观网络和原始网络具有相同的随机游走动力学。具体来说，不同的类型为微观网络合并成宏观节点时边权有不同的处理方式，包括四种处理方法，1）待合并的节点之间没有连边，且输入节点都指向待合并节点，待合并节点都指向相同节点，如图b，输入权重相加，输出权重取平均；2）待合并的节点之间没有连边时，待合并节点指向多个节点时，如图c，输入边权加和，出边的边权按比例加权求和；3）当节点间存在连边时，如图d，需要计算待合并节点的平稳分布，然后采用方法2的方式计算；4）更为复杂的情况，如图e，综合考虑方法2和方法三。