有效信息
有效信息(Effective Information,简称EI)是因果涌现 Causal Emergence理论中的一个核心概念,它可以用来衡量一个马尔科夫动力学的因果效应的强度。这里,一个马尔科夫动力学的因果效应是指这个系统的上一时刻是如何通过动力学以因果的方式对下一个状态产生影响的。具体地,这种因果效应可以通过强制干预系统处于上一时刻的状态为均匀分布或最大熵分布,从而观察系统经由动力学的作用产生的下一时刻的状态分布,那么在这种干预下,上一时刻和下一时刻状态之间的互信息就被定义为有效信息。尽管在有效信息的定义中引入了do操作,但是本质上这一操作是一种名义上的do操作,目的是为了切断与状态本身分布的联系,从而刻画出系统的动力学特性。另外,有效信息通常可以分解为两个部分:确定性(Determinism)和简并性(Degeneracy)。确定性是指,经过动力学的作用,前一时刻的系统状态会唯一确定性地导致下一时刻的系统某一状态的发生的程度;简并性是指:当我们观察到系统的当前状态,就能够唯一确定地推断出系统在上一时刻是处于什么状态的程度。
历史渊源
有效信息(effective informaion,EI)这个概念最早由Giulio Tononi等人在2003年提出,作为整合信息论中的一个关键指标。当一个系统各个组分之间具有很强的因果关联的时候,可以说这个系统具备很高的整合程度,而有效信息:EI便是用来度量这种因果关联程度的关键指标。
后来,到了2013年,Tononi的学生Erik Hoel等人将有效信息这个概念进一步挖掘出来,发现可以用它来很好地定量刻画涌现,于是提出了因果涌现理论。在这个理论中,Hoel使用了Judea Pearl的do算子来改造一般的互信息指标,这使得EI本质上与互信息不同。互信息度量的是相关性,而有效信息因为引入了do算子,从而可以度量因果性。在这一文章中,作者们同时提出了归一化的有效信息指标Eff。
然而,传统的EI主要被用于具有离散状态的马尔科夫链上。为了能过扩充到一般的实数域,P. Chvykov和E. Hoel于2020年合作提出了因果几何理论,将EI的定义扩充到了具备连续状态变量的函数映射上,并通过结合信息几何理论,探讨了EI的一种微扰形式,并与Fisher信息指标进行了比较,提出了因果几何的概念。然而,这一连续变量的EI计算方法需要假设方程中的正态分布随机变量的方差是无限小的,这显然是一种特殊情况。
到了2022年,为了解决一般前馈神经网络的EI计算问题,张江与刘凯威又将因果几何中的连续变量的EI计算方法的方差限制去掉,探讨了EI的更一般形式。然而,这种扩充仍然存在着一个缺陷,由于实数域上变量的均匀分布严格讲是定义在无穷大空间上的,为了避免遭遇无穷大,EI的计算中就会带着一个参数[math]L[/math],表示均匀分布的区间范围。为了避免这个缺陷,也为了在不同粗粒化程度上比较EI,作者们便提出了维度平均EI的概念,并发现由维度平均EI定义的因果涌现度量是一个仅与神经网络的雅可比矩阵的行列式对数值期望与两个比较维度的随机变量方差有关的量,而与其它参量,如[math]L[/math]无关,而且,维度平均EI也可以看作是一种归一化的EI,即Eff。
本质上讲,EI仅仅与一个马尔科夫动力系统的动力学——也就是有关马尔科夫状态转移矩阵有关,而与状态变量的分布无关,然而,这一点在之前的文章中并没有被指出或刻意强调。在2024年的袁冰等人的综述文章,作者们进一步强调了这一点,并给出了EI仅依赖于马尔科夫状态转移矩阵的显式形式。张江等人在最新的讨论动力学可逆性与因果涌现的最新文章中,又指出EI实际上是对底层马尔科夫状态转移矩阵的可逆性的一种刻画,于是尝试直接刻画这种马尔科夫链的动力学可逆性以替代EI。
Do形式及解释
原始的有效信息是定义在离散的马尔科夫链上的。然而,为了能够更广泛地应用,在这里我们探讨有效信息的更一般的形式。
形式定义
考虑两个随机变量:[math]X[/math]和[math]Y[/math],分别代表因变量(Cause Variable)和果变量(Effect Variable),并且假定它们的取值区间分别是[math]\mathcal{X}[/math]和[math]\mathcal{Y}[/math]。同时,[math]X[/math]是通过因果机制[math]f[/math]影响[math]Y[/math]的。所谓的因果机制是指在给定[math]X[/math]取值[math]x\in \mathcal{X}[/math]的情况下,[math]Y[/math]在[math]\mathcal{Y}[/math]上任意取值[math]y\in \mathcal{Y}[/math]的条件概率:
[math]\displaystyle{ f\equiv Pr(Y=y|X=x) }[/math]
则针对这个因果机制[math]f[/math],它所对应的有效信息EI的定义为:
[math]\displaystyle{
EI\equiv I(X:Y|do(X\sim U(\mathcal{X})))=I(\tilde{X}:\tilde{Y})
}[/math]
这里,[math]do(X\sim U(\mathcal{X}))[/math]代表对[math]X[/math]实施do干预(或称do操作),使其服从[math]\mathcal{X}[/math]上的均匀分布[math]U(\mathcal{X})[/math],也即是最大熵分布。[math]\tilde{X}[/math]与[math]\tilde{Y}[/math]分别代表在经过[math]do[/math]干预后的[math]X[/math]和[math]Y[/math]变量,其中,
[math]\displaystyle{ Pr(\tilde{X}=x)=\frac{1}{\#(\mathcal{X})}, }[/math]
这里,[math]\tilde{X}[/math]代表被[math]do[/math]干预后的[math]X[/math]变量,[math]\#(\mathcal{X})[/math]代表集合[math]\mathcal{X}[/math]的基数。对于有限元素集合来说,这就是集合中元素的个数。
在这个干预中,我们要始终保持因果机制[math]f[/math]不变,这就会导致[math]Y[/math]的概率分布发生变化,即被间接干预成为:
[math]\displaystyle{ Pr(\tilde{Y}=y)=\sum_{x\in \mathcal{X}}Pr(X=x) Pr(Y=y|X=x)=\sum_{i\in \mathcal{X}} \frac{Pr(Y=y|X=x)}{\#(\mathcal{X})}. }[/math]
其中,[math]\tilde{Y}[/math]则代表:在保持因果机制[math]f[/math]不变的情况下,[math]Y[/math]变量被[math]X[/math]的do干预所间接改变的变量,这种变化主要体现在概率分布的变化上面。
因此,所谓一个因果机制[math]f[/math]的有效信息EI,就是被干预后的因变量[math]\tilde{X}[/math]和果变量[math]\tilde{Y}[/math]之间的互信息。
为什么要使用do算子?
不难看出,尽管EI本质上就是互信息,但是与传统信息论中的互信息不同,有效信息EI在定义中包含了do操作,即对输入变量做了一个干预操作。为什么要引入这一操作呢?
根据Judea Pearl的因果阶梯理论,即变量之间的因果联系可以被划分为三种层次:关联-干预-反事实。直接对观测数据估测互信息,便是在度量关联程度;而如果我们能对变量做干预操作,即设定变量为某个值或服从某个分布,便上升到了干预的层级;反事实则是设想如果某变量不是当前取值,那么其他变量会是什么样。因此,阶梯层级越高,因果特征越明显。在EI的定义中引入了[math]do[/math]操作,则使得EI能够比互信息更能体现因果特征。
而从实际意义上来讲,在EI的计算中引入do算子,则可以把数据和动力学分开,从而消除数据分布对EI度量所带来的影响。事实上,在一般的因果研究当中,do算子是在消除指向某个变量所有的因果箭头,可以避免混杂因子造成的虚假关联。因此,EI定义中的do算子也可以消除所有指向因变量[math]X[/math]的因果箭头,包括其它变量(包括不客观测的变量)对[math]X[/math]的影响,从而使得EI更能够刻画动力学本身的特性。
do算子的引入让EI这个指标与其他信息度量指标截然不同,关键在于它是且仅是因果机制的函数,一方面这使得它比其他想要刻画因果的指标(比如转移熵)更能抓住因果概念的本质,另一方面它需要你能够已知或获取到因果机制,这在只有观测数据的情况下造成了计算上的困难。
然而,值得指出的是,EI定义里面的do操作
为什么干预成均匀分布?
在Erik Hoel的原始定义中,do操作是将因变量[math]X[/math]干预成了在其定义域[math]\mathcal{X}[/math]上的均匀分布(也就是最大熵分布)。那么, 为什么要干预成均匀分布呢?其它分布是否也可以?
首先,根据上一小节的论述,do操作的实质是希望让EI能够更清晰地刻画因果机制[math]f[/math]的性质,因此,需要切断因变量[math]X[/math]与其它变量的联系,并改变其分布,让EI度量与[math]X[/math]的分布无关。
而之所以要把输入变量干预为最大熵下的均匀分布,其实就是要更好地刻画因果机制的特性。为什么这么说呢?
当[math]\mathcal{X}[/math]和[math]\mathcal{Y}[/math]都是有限可数集合的时候,因果机制[math]f\equiv Pr(Y=y|X=x)[/math]就成为了一个[math]\#(\mathcal{X})[/math]行[math]\#(\mathcal{Y})[/math]的矩阵,我们可以展开EI的定义:
[math]\displaystyle{
EI = I(X,Y|do(X)\sim U)= \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}Pr(X=x,Y=y)\log \frac{Pr(X=x,Y=y)}{Pr(X=x)Pr(Y=y)}\\
= \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}Pr(X=x)Pr(Y=y|X=x)\log \frac{Pr(Y=y|X=x)}{Pr(Y=y)}\\
= \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}Pr(X=x)Pr(Y=y|X=x)\log Pr(Y=y|X=x)- \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}Pr(X=x)Pr(Y=y|X=x)Pr(Y=y) \\
=\frac{1}{\#(\mathcal{X})} (-H(Pr(Y|X)) + H(Pr(Y))
}[/math]
不难看出,最后得到的等式告诉我们,EI实际上由两项构成,第一项是因果机制矩阵每一行的负熵的平均值,第二项则是变量[math]Y[/math]的熵。
在第一项中,[math]X[/math]的概率分布实际上起到了对每一行的熵求平均时候的权重的作用。只有当我们将该权重取为同样的数值的时候,才能够平等地对待因果机制矩阵中的每一个行,这时就恰好是将[math]X[/math]do成均匀分布的时候。
如果不是均匀分布,也就意味着某些行的熵就会被乘以一个较大的权重,有的行就会被赋予一个较小的权重,因此也就不能做到让EI能够反映因果机制的天然属性。
Markovian matrix 形式(TPM)
Erik Hoel进一步将EI应用在一个随机过程的背景下,输入变量为[math]\displaystyle{ X_t }[/math],输出变量为[math]\displaystyle{ X_{t+1} }[/math],在将[math]\displaystyle{ X_t }[/math]干预为最大熵分布时,计算二者之间的互信息。在离散情况下,最大熵分布即为均匀分布。因为这里的EI计算只关乎两个时刻,在干预的情况下更早的历史变量不起作用,所以Hoel假定该过程的动力学就是一个满足马尔科夫性的概率转移矩阵。下面给出几个马尔科夫概率转移矩阵的示例。
马尔科夫矩阵中每个元素都是一个条件概率,满足行归一化。将输入变量概率分布和矩阵直接相乘便得到输出变量的概率分布。因为有干预,所以EI的大小只和转移矩阵本身有关。已知马尔科夫概率转移矩阵,我们可以用下式计算EI。
[math]\displaystyle{
EI = I(X_t,X_{t+1}|do(X_t)\sim U) \\
= \sum^N_{\tilde{x}_t}\sum^N_{\tilde{x}_{t+1}}p(\tilde{x}_t,\tilde{x}_{t+1})\log \frac{p(\tilde{x}_t,\tilde{x}_{t+1})}{p(\tilde{x}_t)p(\tilde{x}_{t+1})}\\
= \sum^N_{\tilde{x}_t}p(\tilde{x}_t)\sum^N_{\tilde{x}_{t+1}}p(\tilde{x}_{t+1}|\tilde{x}_t)\log \frac{p(\tilde{x}_{t+1}|\tilde{x}_t)}{p(\tilde{x}_{t+1})}\\
= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{p_{ij}}{\overline{p}_j}\\
= \frac{1}{N}\sum^N_{i=1}D_{KL}(P_{i.}||\overline{P})
}[/math]
其中N为状态数,[math]\displaystyle{ \tilde{x}_t,\tilde{x}_{t+1} }[/math]分别为把t时刻的输入干预为最大熵分布后前后两个时刻的状态。[math]\displaystyle{ p_{ij} }[/math]为第i个状态转移到第j个状态的转移概率。将矩阵每列求均值,可得到平均转移向量[math]\displaystyle{ \overline{P} }[/math],每个分量便是[math]\displaystyle{ \overline{p}_j }[/math]。我们也可以用KL散度的方式来表达:EI是转移矩阵每个行转移向量与平均转移向量的KL散度的均值。
归一化
显然,EI的大小和状态空间大小有关,我们需要做一个归一化,得到和系统尺寸无关的一个量化指标。根据Tononi等人的工作,要用最大熵分布下的熵值来做分母,那么在马尔科夫转移矩阵的背景下,该值便等于[math]\displaystyle{ \log_2N }[/math]。进一步定义归一化指标有效性(effectiveness)为[math]\displaystyle{ eff=\frac{EI}{\log_2N} }[/math]。
后来,在神经信息压缩器(Neural information squeezer, NIS)提出时,构建了直接对状态空间维度求平均的指标dEI。[math]\displaystyle{ dEI=\frac{EI}{N} }[/math],这同样可以消除系统大小带来的影响。在离散的系统中,dEI和有效性实际上是等价的。
因果涌现(CE)
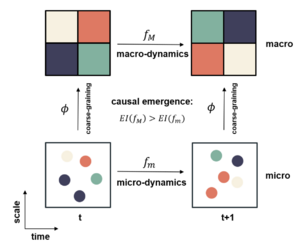
有了有效信息这一度量指标后,因果涌现的框架可以被呈现出来了。对于一个系统,观察者可以建立多尺度视角去观测,区分出微观和宏观。收集到的微观数据可以直接反映微观动力学,在经过粗粒化映射(coarse-graining)后,由微观变量得到对应的宏观变量,也自然会有相应的宏观动力学。对两个动力学分别可以计算EI,如果宏观EI大于微观EI,认为有因果涌现发生。
这里有一个新的指标直接度量因果涌现的程度:
[math]\displaystyle{ CE = EI(TPM_M) - EI(TPM_m) }[/math]
也可以计算归一化后的CE:
[math]\displaystyle{ dCE(TPM_M,TPM_m) = \frac{EI(TPM_M)}{n_M} - \frac{EI(TPM_m)}{n_m} }[/math]
确定性和简并性
考察归一化后的eff,我们可以将其拆成两部分,分别对应确定性(determinism)和简并性(degeneracy)。
[math]\displaystyle{ Eff = Determinism - Degeneracy }[/math]
我们可以在给定TPM的情况下,写出它们的表达式。
[math]\displaystyle{ Determinism = \frac{1}{\log_2N}\sum_{i,j}TPM(i,j)\log_2{(N\times TPM(i,j))} \\ Degeneracy = \frac{1}{\log_2N}\sum_{i,j}TPM(i,j)\log_2{(\sum_k TPM(k,j))} }[/math]
关键在于理解它们的物理含义。确定性指的是,已知当前时刻状态概率分布,对未来可能状态的判断有多大的把握;而简并性指的是,已知当前的状态,追溯历史,我们能有多大确定性做出判断。如果有状态在动力学过程中发生简并,我们回溯历史时能运用的信息就会变少。当一个系统背后的动力学确定性高,同时简并性低时,说明这是一个具有明显因果效应的动力学。这就是EI本身的物理含义。
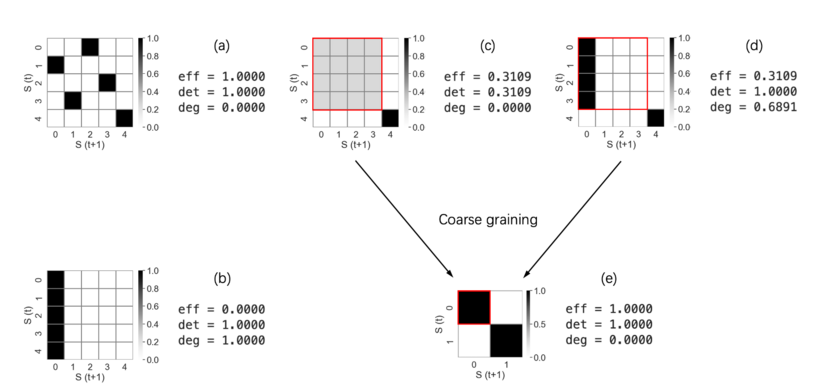
上图展示了几种TPM,其中(a)是确定性高,简并性低,所以整体eff比较高。(b)则是确定性和简并性都比较高,所以eff是0。(c)相比于(a)确定性更低,(d)也是确定性和简并性都较高导致eff较低,它们都可以通过同一种粗粒化策略(将前4个状态合并为一个状态)来得到(e)。此时(e)确定性很高,无简并性,所以(e)的eff比(c)(d)要高。
连续系统的EI
见其他词条
整合信息论中的EI
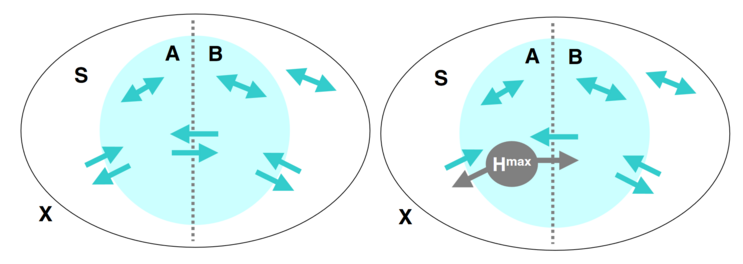
整合程度(或者叫整合信息能力)[math]\displaystyle{ \Phi }[/math],可以被定义为系统一个子集两个互补部分之间可交换的有效信息最小值。假如系统是X,S是X的一个子集,它被划分为两个部分,分别是A和B。A、B之间以及它们跟X中其余的部分都存在着相互作用和因果关系。
这时,我们可以度量这些因果关系的强弱。首先,我们来计算从A到B的有效信息,即让A服从最大熵分布时,度量A和B之间的互信息。
[math]\displaystyle{ EI(A\rightarrow B) = MI(A^{H^{max}}: B) }[/math]
如果A的不同状态会导致B有很不一样的变化,这个EI值会很高;反之,如果无论A怎么变,B都受到很少的影响,那么EI就会很低。显然,这种度量是有方向的,A对B的EI和B对A的EI可以很不同。我们可以把这两个方向的EI加在一起,得到S在某一个划分下的EI大小。
[math]\displaystyle{ EI(A\leftrightarrow B) = EI(A\rightarrow B) + EI(B\rightarrow A) }[/math]
遍历各种划分,如果存在某一个划分,使得EI为0,说明这个S可以被看做是两个因果独立的部分,所以整合程度也应该是0。从这种特殊例子中我们可以看出,我们应该关注所有划分中有效信息最小的那个。当然,不同划分会导致A和B的状态空间就不一样,所以应该做一个归一化处理,即除以A和B最大熵值中较小的那一个。于是,我们可以有一个最小信息划分(minimum information bipartition,MIB)。整合程度[math]\displaystyle{ \Phi }[/math]定义如下:
[math]\displaystyle{ \Phi(S) = EI(MIB(S)) }[/math]
代码
python:
def tpm_ei(tpm, log_base = 2): # marginal distribution of y given x ~ Unifrom Dist puy = tpm.sum(axis=0) n = tpm.shape[0] # replace 0 to a small positive number to avoid log error eps = 1E-10 tpm_e = np.where(tpm==0, eps, tpm) puy_e = np.where(tpm==0, eps, puy) # calculate EI of specific x ei_x = (np.log2(n * tpm_e / puy_e) / np.log2(log_base) * tpm).sum(axis=1) # calculate total EI ei_all = ei_x.mean() return ei_all
参考文献
Hoel, E. P., Albantakis, L., & Tononi, G. (2013). Quantifying causal emergence shows that macro can beat micro. Proceedings of the National Academy of Sciences, 110(49), 19790–19795. https://doi.org/10.1073/pnas.1314922110
Tononi, G., & Sporns, O. (2003). Measuring information integration. BMC Neuroscience.
Yuan, B., Zhang, J., Lyu, A., Wu, J., Wang, Z., Yang, M., Liu, K., Mou, M., & Cui, P. (2024). Emergence and Causality in Complex Systems: A Survey of Causal Emergence and Related Quantitative Studies. Entropy, 26(2), 108. https://doi.org/10.3390/e26020108