复杂网络中的因果涌现
复杂网络中的因果涌现是指在复杂网络系统中,通过合适的粗粒化策略使得系统在宏观尺度展现出比微观尺度更强的因果特性。复杂网络的研究涉及多个领域,包括物理学、生物学、计算机科学和社会科学等。这些网络通常由节点和连接这些节点的边组成,节点可以代表个体或元素,而边则代表它们之间的相互作用或联系。因果涌现理论最初是由Erik Hoel[1]等人提出,并提出使用有效信息(Effective Information,简称EI)来量化离散马尔科夫动力学系统的因果性强弱。2020 年,Klein 等人[2]尝试将该方法应用到复杂网络中,在更宏观的尺度上粗粒化网络并观察其EI相比原始网络如何变化,当粗粒化网络(宏观尺度)比原始网络 (微观尺度)具有更高的 EI 时,则说明该网络发生了因果涌现。
历史渊源
复杂网络的研究可以追溯到1736年欧拉解决哥尼斯堡七桥问题,而现代复杂网络理论则主要发展于20世纪末。欧拉通过研究哥尼斯堡的七桥问题,提出了图论的基本概念,这奠定了复杂网络分析的基础。在20世纪60年代,Erdos和Renyi提出了随机图论[3],这是首个系统性的网络模型,用于描述和分析大规模随机网络的特性。到了90年代,随着计算机能力的提升和互联网的发展,复杂网络的研究取得了突破性进展。1998年,Watts和Strogatz在《Nature》上发表了关于小世界网络[4]的论文,揭示了许多实际网络中存在的“六度分离”现象。次年,Barabási和Albert在《Science》上提出了无标度网络模型[5],强调了实际网络中节点连接度的幂律分布特性。进入21世纪后,复杂网络理论吸引了来自数学、物理学、计算机科学、社会学等多个领域的研究者,成为一门交叉学科。
因果涌现理论的历史发展可以追溯到古希腊哲学,是在涌现和复杂系统理论的背景下逐渐形成,在古希腊哲学家亚里士多德的《Metaphysics》中,涌现的概念初现端倪,他认为整体是超越于部分的东西,强调“整体大于部分之和”。20世纪40年代,控制论的创始人维纳和冯·诺伊曼通过研究系统及其因果反馈回路,为复杂系统提供了早期的理论基础[6]。1999年,经济学家杰弗里•戈尔茨坦 Jeffrey Goldstein在《Emergence》杂志上提出了现有的对“涌现”的定义[7]。戈尔茨坦最初将涌现定义为:“在复杂系统自组织过程中产生的新颖而连贯的结构、模式和性质”。2013年,Erik Hoel和他的团队首次提出了因果涌现理论[1],使用有效信息(Effective Information, EI)来量化离散马尔科夫动力学系统的因果性强弱。
2020年Klein等人在尝试将因果涌现理论应用于复杂网络[2],并提出了一系列技术方法,主要步骤为:定义复杂网络节点动力学(引入随机游走子,假定每个节点具有随机游走动力学),定义有效信息(基于节点的概率转移矩阵,类比状态转移矩阵的有效信息计算方式),粗粒化复杂网络(考虑不同的粗粒化方法,将微观节点粗粒化为宏观节点)、检验动力学的一致性(保证粗粒化完以后的网络具有相同的随机游走动力学)。
定义复杂网络节点动力学
由于因果涌现理论量化的是系统的动力学,对于离散马尔科夫动力学来说就是状态转移矩阵TPM,然而对于复杂网络来说,给定一个网络已知不具有动力学,需要人为定义复杂网络节点的动力学,可以借助随机游走子定义网络中的马尔科夫链,从而假定网络中的每个节点具有随机游走动力学,并且此时的转移矩阵也是节点间的状态转移。
定义有效信息
将随机游走子放在节点上,等价于对节点做干预[math]\displaystyle{ do(·) }[/math],基于随机游走概率可以定义节点的转移概率矩阵,建立了有效信息与网络连通性的联系,将网络节点类比系统状态构建网络动力学的有效信息。
网络中的连通性可通过节点出边与入边的权重的不确定性来表征,包括两项:
1)节点输出的不确定性可通过节点出权的香农熵定义,即[math]\displaystyle{ H(W_i^{out}) }[/math],因此整个网络的不确定性可通过[math]\displaystyle{ \lt H(W_i^{out})\gt }[/math]得到,[math]\displaystyle{ W_i^{out} }[/math]是节点[math]\displaystyle{ v_i }[/math]的转移向量;
2)基于网络的出边权重分布计算,[math]\displaystyle{ H(\lt W_i^{out}\gt ) }[/math]反映了确定性如何在网络中分布。通过这2项就可得到复杂网络中的有效信息定义,输入[math]\displaystyle{ w_{ij} }[/math]是节点[math]\displaystyle{ i }[/math]和[math]\displaystyle{ j }[/math]之间的转移概率,输出是有效信息值。
[math]\displaystyle{ \begin{aligned} {J} &=\frac{1}{N}\sum_{i=1}^ND_{KL}[W_i^{out}||\lt W_i^{out}\gt ] \\ &= \frac{1}{N}\sum_{i=1}^N\sum_{j=1}^Nw_{ij}\log_2(w_{ij})-\frac{1}{N}\sum_{i=1}^N\sum_{j=1}^Nw_{ij}\log_2(W_j) \\ &= H(\lt W_i^{out}\gt )-\lt H(W_i^{out})\gt \end{aligned} }[/math]
其中,对于一个无权图来说转移概率[math]\displaystyle{ w_{ij} }[/math]等于节点[math]\displaystyle{ i }[/math]的度的倒数,对于一个加权图来说转移概率[math]\displaystyle{ w_{ij} }[/math]等于节点[math]\displaystyle{ i }[/math]出边权重值的归一化,[math]\displaystyle{ W_i^{out} }[/math]由[math]\displaystyle{ v_i }[/math]和它的邻居[math]\displaystyle{ v_j }[/math]之间的转移概率[math]\displaystyle{ w_{ij} }[/math]组成,如果没有从[math]\displaystyle{ v_i }[/math]到[math]\displaystyle{ v_j }[/math]的边,则[math]\displaystyle{ w_{ij}=0 }[/math],对于每个[math]\displaystyle{ W_i^{out} }[/math],[math]\displaystyle{ ∑_jW_i^{out}=1 }[/math]。[math]\displaystyle{ W_j=\frac{1}{N}\sum_{i=1}^N w_{ij} }[/math],表示节点的平均分布。 同样进一步,有效信息可以分解为确定性和简并性。
粗粒化复杂网络
为了识别复杂网络中的因果涌现,需要对网络进行粗粒化,然后比较宏观网络与微观网络的有效信息,判断能否发生因果涌现。粗粒化方法包括:贪婪算法、谱分解方法以及梯度下降方法。Klein等人[2]利用贪婪算法构建了宏观尺度的网络,发现对于大规模网络其效率很低。Griebenow 等人[8]提出了一种基于谱分解的方法识别偏好依赖网络中的因果涌现。相较于贪婪算法以及梯度下降算法,谱分解算法的计算时间最少,同时找到宏观网络的因果涌现也更加显著。
贪婪算法
- 初始化一个队列,随机选择一个节点[math]\displaystyle{ v_i }[/math](没有访问过的), 将[math]\displaystyle{ v_i }[/math]所属的邻域(马尔可夫毯 )[math]\displaystyle{ B_{v_i} }[/math] 中的节点加入队列中
- 初始时[math]\displaystyle{ v_{\mu} }[/math]=[math]\displaystyle{ v_i }[/math]
- 分别尝试将 [math]\displaystyle{ v_{\mu} }[/math] 与 [math]\displaystyle{ v_j }[/math][math]\displaystyle{ \in }[/math][math]\displaystyle{ B_{v_i} }[/math] 合并:
- 如果合并后的网络的EI增加了,就将这两个节点合并组成新的宏观节点[math]\displaystyle{ v_{\mu} }[/math],将[math]\displaystyle{ v_j }[/math]所属的邻域中的不在队列中的节点加入队列中
- EI没增加则继续尝试与队列中的其他节点进行合并,直至队列中的节点都合并过,返回步骤1
时间复杂度:[math]\displaystyle{ O(N^4) }[/math]
谱分解方法
- 输入一个网络[math]\displaystyle{ A_m }[/math],得到其转移矩阵[math]\displaystyle{ T_{Am} }[/math],然后进行矩阵的特征值分解,得到特征值[math]\displaystyle{ Λ=\{λ_i\} }[/math]与特征向量[math]\displaystyle{ E=\{e_i\} }[/math],构建新的[math]\displaystyle{ E’=\{λ_ie_i|λ_i≠0\} }[/math](新的网络节点数量为[math]\displaystyle{ N' }[/math])
- 依据[math]\displaystyle{ E' }[/math]计算节点间的距离矩阵[math]\displaystyle{ D_{N'×N'} }[/math]:
- 基于距离矩阵[math]\displaystyle{ D_{N'×N'} }[/math],使用OPTICS算法进行聚类,同一类里的节点进行粗粒化作为一个宏观节点,存在距离超参[math]\displaystyle{ \epsilon }[/math],需要线性搜索,选择EI最大的参数
时间复杂度:[math]\displaystyle{ O(N^3) }[/math]
梯度下降方法
由于EI是不可微的,所以梯度下降法不能直接适用。
解决方法:针对一个含有[math]\displaystyle{ 𝑛 }[/math]个节点的网络,定义一个分组矩阵[math]\displaystyle{ M\in R^{n×k} }[/math],其中[math]\displaystyle{ m_{iμ}=Pr(v_i\in v_{\mu}) }[/math],表示微节点[math]\displaystyle{ v_i }[/math]属于宏观节点[math]\displaystyle{ v_{\mu} }[/math]的概率,然后根据微观网络和分组矩阵构建宏观网络,优化目标是最大化宏观网络的有效信息EI,使用带动量的梯度下降方法优化[math]\displaystyle{ M }[/math]。
时间复杂度:[math]\displaystyle{ O(N^3) }[/math]
困难:
- 初始化分组矩阵的选择,多次重复实验会得到不一样的结果
- 依赖神经网络的超参,如学习率、迭代次数等
宏节点合并方法
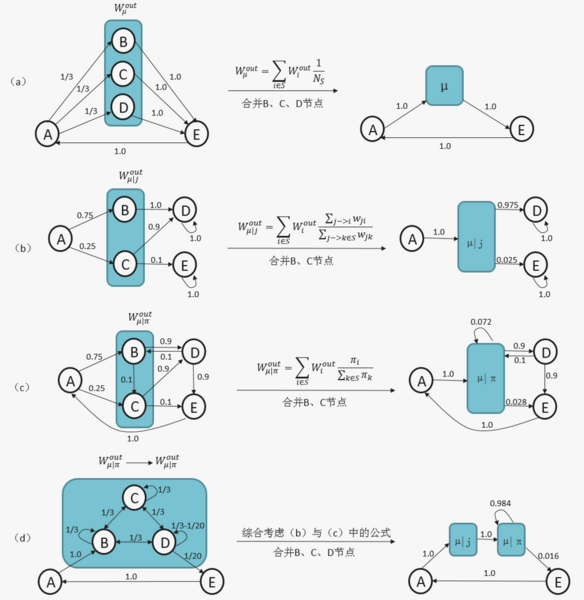
通过上面的网络粗粒化方法可以对节点进行分组,从而可以构建宏观网络。将微观节点合并成宏观节点时,对应宏观网络的转移概率矩阵也要进行相应的处理。通过使用高阶节点显式地对高阶依赖项建模(HOMs),保证分组后的宏观网络和原始网络具有相同的随机游走动力学。
具体来说,不同的类型的微观节点合并成宏观节点时边权有不同的处理方式,包括四种处理方法:
1)待合并的节点之间没有连边,且输入节点都指向待合并节点,待合并节点都指向相同输出节点时,如图a所示,需要将输入权重相加,输出权重取平均,其中[math]\displaystyle{ Ns }[/math]为合并节点的数量[math]\displaystyle{ (W_{\mu}^{out}=\sum_{i \in S}W_i^{out}\frac{1}{N_S}) }[/math];
2)待合并的节点之间没有连边且待合并节点指向多个节点时,如图b所示,需要将输入边权加和,出边的边权按比例加权求和,其中[math]\displaystyle{ w_{ji} }[/math]为节点[math]\displaystyle{ v_i }[/math]的入边权重[math]\displaystyle{ (W_{\mu|j}^{out}=\sum_{i \in S}W_i^{out}\frac{\sum_{j-\gt i}w_{ji}}{\sum_{j-\gt k\in S}w_{jk}}) }[/math];
3)当待合并节点间存在连边时,如图c所示,需要计算待合并节点的平稳分布,然后采用方法2的方式计算,其中 [math]\displaystyle{ π_i }[/math]为节点[math]\displaystyle{ v_i }[/math]在网络平稳分布中的概率[math]\displaystyle{ (W_{\mu|\pi}^{out}=\sum_{i \in S}W_i^{out}\frac{\pi_i}{\sum_{k\in S}\pi_k}) }[/math];
4)更为复杂的情况,如图d所示,综合考虑方法2和方法3。
检验动力学的一致性
动力学的一致性检验可以进一步验证HOMs方法的有效性,公式如下所示,比较宏微观网络节点在不同时刻的概率分布的KL散度之和。实验发现在不同节点规模以及参数下的偏好依附网络的粗粒化后的宏观网络的不一致性随着迭代步数的增加都会收敛到0。
在微观网络[math]\displaystyle{ G }[/math]与宏观网络[math]\displaystyle{ G_M }[/math]上随机游走,在未来某个时间[math]\displaystyle{ t }[/math] , [math]\displaystyle{ G }[/math]上的预期分布为 [math]\displaystyle{ P_m(t) }[/math], [math]\displaystyle{ G_M }[/math]上的预期分布为 [math]\displaystyle{ P_M(t) }[/math]。将[math]\displaystyle{ P_m(t) }[/math]分布叠加到宏观上[math]\displaystyle{ G_M }[/math]的相同节点上,得到[math]\displaystyle{ P_{M|m}(t) }[/math]分布。用[math]\displaystyle{ P_M(t) }[/math]和[math]\displaystyle{ P_{M|m}(t) }[/math]之间的KL散度来衡量其不一致性(inconsistency),若结果为零则动力学一致。公式为:
[math]\displaystyle{ inconsistency=\sum_{t=0}^T D_{KL}[P_M(t)||P_{M|m}(t)] }[/math]
复杂网络中的有效信息
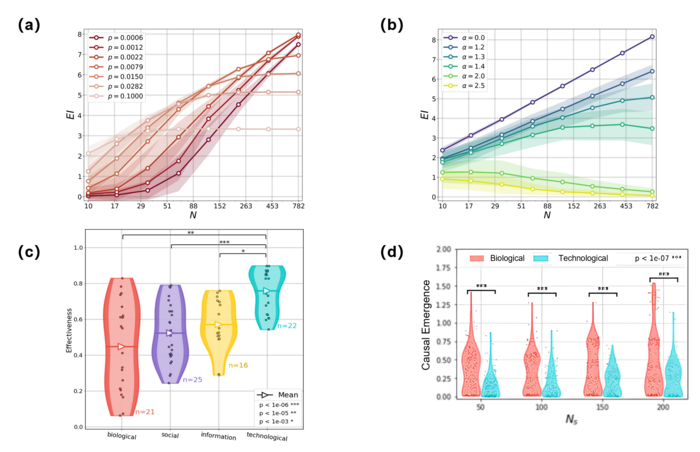
2020年Klein等人在一篇论文[2]中分析了随机(ER)、偏好依赖(PA)等人工网络,以及生物、社会、信息和技术4类真实网络的有效信息(EI)。
人工网络
1)对于ER网络,有效信息的大小只依赖连接概率 [math]\displaystyle{ p }[/math],并且随着网络规模的增大有效信息会收敛到[math]\displaystyle{ -\log_2p }[/math]。在某点之后,ER网络结构不会随着其规模的增加而包含更多的信息,这个相变点近似在网络的平均度 [math]\displaystyle{ \lt k\gt }[/math]=[math]\displaystyle{ \log_2N }[/math] 的位置。随着ER网络连接概率的增大,巨连通集团相变点位置对应出现,如图a所示。
2)对于PA 网络:[math]\displaystyle{ \alpha\lt 1.0 }[/math]时,有效信息的大小随着网络规模的增加而增大;[math]\displaystyle{ \alpha\gt 1.0 }[/math]时,结论相反; [math]\displaystyle{ \alpha=1.0 }[/math]对应的无标度网络则是增长的临界边界,如图b所示。
真实网络
对于真实网络,生物网络因为具有很大的噪声,所以有效信息最低,通过有效的粗粒化能去除这些噪声。相较于其他类型,因果涌现最显著;技术类型网络是更稀疏、非简并的网络,因此,平均效率更高,节点关系更加具体,所有有效信息也最大,如图c、d所示。
代码
参考:https://github.com/jkbren/einet
参考文献
- ↑ 1.0 1.1 Hoel E P, Albantakis L, Tononi G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49): 19790-19795.
- ↑ 2.0 2.1 2.2 2.3 Klein B, Hoel E. The emergence of informative higher scales in complex networks[J]. Complexity, 2020, 20201-12.
- ↑ Erdős, P.; Rényi, A.(1959). On random graphs I. Publ. math. debrecen, 6(290-297), 18.
- ↑ Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’networks. Nature, 393(6684), 440-442.
- ↑ Barabási, A. L., & Albert, R. (1999). Emergence of scaling in random networks. Science, 286(5439), 509-512.
- ↑ Wiener, N. (2019). Cybernetics or Control and Communication in the Animal and the Machine. MIT press.
- ↑ Goldstein, Jeffrey. "Emergence as a Construct: History and Issues". Emergence. 1.1 (1999): 49-72.
- ↑ Griebenow R, Klein B, Hoel E. Finding the right scale of a network: efficient identification of causal emergence through spectral clustering[J]. arXiv preprint arXiv:190807565, 2019.
编者推荐
下面是一些链接能够帮助读者更好的了解因果涌现的相关信息:
因果涌现读书会
分享近期发展起来的一些理论与工具,包括因果涌现理论、机器学习驱动的重整化技术,以及自指动力学正在发展一套跨尺度的分析框架等。
涌现现象无非是复杂系统中诸多现象中最神秘莫测的一个,而Erik Hoel提出的“因果涌现”理论为这种跨层次的奇妙涌现现象提供了一种新的可能解释途径。通过跨层次的粗粒化(Coarse-graining, 或称重整化Renormalization)操作,我们便可以在同一个动力学系统上在不同的尺度得到完全不同的动力学,通过本季读书会梳理,我们希望探讨这一新兴领域的前沿进展,衍生更多新的研究课题。
涌现与因果的结合创造了因果涌现的概念。这是一套利用因果性来定量刻画涌现的理论体系,本季读书会通过阅读前沿文献,加深我们对因果、涌现等概念的理解;聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。第二季读书会更加集中在探讨因果科学与因果涌现之间的关系,以及对涌现进行定量刻画,聚焦于寻找因果与涌现、多尺度等概念相结合的研究方向;并探索复杂系统多尺度自动建模的研究方向。
因果涌现第三季的读书会中,将进一步围绕因果涌现的核心研究问题『因果涌现的定义』以及『因果涌现的辨识』来进行深入的学习和讨论,对 Erik Hoel 提出的 Causal Emergence,Causal Geometry 等因果涌现的核心理论进行深入的探讨和剖析,并且详细梳理其中涉及到的方法论,包括从动力学约简、隐空间动力学学习等其他研究领域中学习和借鉴相关的研究思路,最后探讨因果涌现的应用,包括基于生物网络、脑网络或者涌现探测等问题展开扩展,发掘更多的实际应用场景。
此次读书会将首先对信息论领域进行整体回顾,介绍经典信息指标,希望建立对信息熵的直觉,给后面的内容打基础。第二部分介绍整合信息论的理论框架。第三部分将详细梳理信息分解的理论框架,包括部分信息分解(PID)、延展的PID框架、信息分解计算,以及信息论在脑与复杂系统中的应用。最后介绍整合信息分解(ΦID)与 Rosas 的因果涌现框架。
本季读书会分成两部分,一部分是有关因果涌现理论方面的最新进展,包括信息分解的定量化、动力学可逆性与因果涌现,以及复杂系统的低秩表示理论、本征微观态理论等,第二部分是这些理论在脑科学及其它学科上的应用。
路径推荐
- 张江老师根据因果涌现读书会第一季梳理的关于因果涌现的学习路径:https://pattern.swarma.org/article/153
- 张江老师根据因果涌现读书会梳理的关于因果涌现的入门学习路径:https://pattern.swarma.org/article/296
此词条由王志鹏、刘易明编写,张江、王志鹏、刘易明整理和审校。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。