有效信息
有效信息(Effective Information,简称EI)是因果涌现 Causal Emergence理论中的一个核心概念,它可以用来衡量一个马尔科夫动力学的因果效应的强度。这里,因果效应是指把动力学看做一个黑箱,那么不同的输入分布就会导致不同的输出分布,二者之间联系的紧密程度就是因果效应。有效信息通常可以分解为两个部分:确定性(Determinism)和简并性(Degeneracy)。确定性是指,在动力学的作用下,我们根据系统前一时刻的状态会以多大程度预测它下一时刻状态;简并性是指:我们能够以多大程度从下一时刻的状态预测上一时刻的状态。如果确定性越大,或简并性越小,则系统的有效信息就会越大。在本页中,所有的[math]\log[/math]都表示以2为底的对数运算。
历史渊源
有效信息(effective informaion,EI)这个概念最早由Giulio Tononi等人在2003年提出[1],作为整合信息论中的一个关键指标。当一个系统各个组分之间具有很强的因果关联的时候,可以说这个系统便具备很高的整合程度,而有效信息:EI,便是用来度量这种因果关联程度的关键指标。
到了2013年,Giulio Tononi的学生Erik Hoel等人将有效信息这个概念进一步提炼出来,从而定量地刻画涌现,于是提出了因果涌现理论[2]。在这个理论中,Hoel使用了Judea Pearl的do算子来改造一般的互信息指标[3],这使得EI本质上与互信息不同。互信息度量的是相关性,而有效信息因为引入了do算子,从而可以度量因果性。在这一文章中,作者们同时提出了归一化的有效信息指标Eff。
然而,传统的EI主要被用于具有离散状态的马尔科夫链上。为了能扩充到一般的实数域,P. Chvykov和E. Hoel于2020年合作提出了因果几何理论[4],将EI的定义扩充到了具备连续状态变量的函数映射上,并通过结合信息几何理论,探讨了EI的一种微扰形式,并与Fisher信息指标进行了比较,提出了因果几何的概念。然而,这一连续变量的EI计算方法需要假设方程中的正态分布随机变量的方差是无限小的,这一要求显然过于苛刻了。
到了2022年,为了解决一般前馈神经网络的EI计算问题,张江与刘凯威又将因果几何中的连续变量的EI计算方法的方差限制去掉,探讨了EI的更一般形式[5][6][7]。然而,这种扩充仍然存在着一个缺陷,由于实数域上变量的均匀分布严格讲是定义在无穷大空间上的,为了避免遭遇无穷大,EI的计算中就会带着一个参数[math]L[/math],表示均匀分布的区间范围。为了避免这个缺陷,也为了在不同粗粒化程度上比较EI,作者们便提出了维度平均EI的概念,并发现由维度平均EI定义的因果涌现度量是一个仅与神经网络的雅可比矩阵的行列式与两个比较维度的随机变量方差有关的量,而与其它参量,如L无关,而且,维度平均EI也可以看作是一种归一化的EI,即Eff。
本质上讲,EI仅仅与一个马尔科夫动力系统的动力学——也就是与马尔科夫状态转移矩阵有关,而与状态变量的分布无关的量,然而,这一点在之前的文章中并没有被指出或刻意强调。在2024年的袁冰等人的综述文章中,作者们进一步强调了这一点,并给出了EI仅依赖于马尔科夫状态转移矩阵的显式形式[8]。张江等人在最新的讨论动力学可逆性与因果涌现的文章中,又指出EI实际上是对底层马尔科夫状态转移矩阵的可逆性的一种刻画,于是尝试直接刻画这种马尔科夫链的动力学可逆性以替代EI[9]。
简介
有效信息(EI)指标主要用来度量马尔科夫动力学的因果效应强度。与一般的因果推断理论不同,EI主要用于动力学(马尔科夫的转移概率矩阵)已知,且不存在未知变量即混杂因子的情况。其核心目标是度量因果关联强度,而并非是否存在因果效应。也就是说,EI更适用于已经确知了因果变量X和Y之间存在着因果联系的场合。
更正式地,EI是因果机制(在离散状态的马尔科夫链中,是这个马尔科夫链的概率转移矩阵)的函数,而与其它因素无关。EI的正式定义为:
[math]\displaystyle{ EI(P)\equiv I(Y;X|do(X\sim U)) }[/math]
这里,P代表X到Y的因果机制,它是一个概率转移矩阵,即[math]p_{ij}\equiv Pr(Y=j|X=i)[/math];X是因变量,Y是果变量,[math]do(X\sim U)[/math]表示对因变量X进行do干预,将X的分布变为均匀分布。在这一干预下,同时假设X到Y的因果机制P保持不变,那么,Y就会间接地受到X的do干预的影响而发生变化。则EI度量的是经过干预后的X和Y之间的互信息。
之所以引入do操作,目的是为了消除数据X的分布对EI的影响,以使得最后的EI度量仅仅是因果机制f的函数,而与数据X无关。
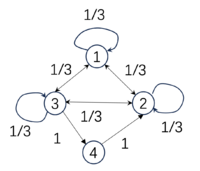
下面,给出三个马尔科夫链的例子,以及相应的EI数值也放到了下面:
|
[math]\displaystyle{ P_1=\begin{pmatrix} &0 &0 &1 &0& \\ &1 &0 &0 &0& \\ &0 &0 &0 &1& \\ &0 &1 &0 &0& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_2=\begin{pmatrix} &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &0 &0 &0 &1& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_3=\begin{pmatrix} &0 &0 &1 &0& \\ &1 &0 &0 &0& \\ &1 &0 &0 &0& \\ &1 &0 &0 &0& \\ \end{pmatrix} }[/math]. |
| [math]\begin{aligned}&EI(P_1)=2\ bits,\\&Det(P_1)=2\ bits,\\&Deg(P_1)=0\ bits\end{aligned}[/math] | [math]\begin{aligned}&EI(P_2)=0.81\ bits,\\&Det(P_2)=0.81\ bits,\\&Deg(P_2)=0\ bits\end{aligned}[/math] | [math]\begin{aligned}&EI(P_3)=0.81\ bits\\&Det(P_3)=2\ bits,\\&Deg(P_3)=1.19\ bits.\end{aligned}[/math] |
-
(example)
我们可以看到,第一个矩阵[math]P_1[/math]的EI比第二个[math]P_2[/math]的高,这是因为这一概率转移是一个完全确定性的转移,也就是从某一个状态出发,它会以100%的概率转移到另外某一个状态。然而,并不是所有的确定性转移的矩阵都会对应较大的EI,比如[math]P_3[/math]这个矩阵,虽然它的转移概率也都是100%或0,但是因为所有后面三种状态都会转移到第1个状态,因此我们将无法区分它上一时刻是处于何种状态的。这种情况下它的EI也会比较低,我们称这种情况存在着简并性。于是,如果一个转移矩阵具有较高的确定性和较低的简并性,则它的EI就会很高。进一步,存在如下对EI的分解:
[math]\displaystyle{ EI=Det-Deg }[/math]
这里,Det是对确定性(Determinism)的缩写,而Deg是对简并性(Degeneracy)的缩写,EI是二者之差。在上面的表格中,我们将矩阵所对应的Det和Deg数值也都列在了下面。
第一个转移概率矩阵是一个排列矩阵(Permutation),它是可逆的,因此确定性最高,没有简并性,因而EI最大;第二个矩阵的前三个状态都会以1/3的概率跳转到彼此,因此确定性程度最低,而简并性也很低,EI是0.81;第三个矩阵虽然也是非0即1的转移概率,因而确定性最高,但是由于后三个状态都跳转到1,因此,从1状态不能推知它来自于哪个状态,因此简并性最高,最终的EI与第二个相同,仍然是0.81。
尽管在原始文献中[2],有效信息大多应用于离散状态的马尔科夫链,但是,张江、刘凯威、杨明哲等人将EI的定义扩展到了更一般的连续变量的情形[5][6][7]。这一扩充的基本思想是从EI的原始定义出发,将因变量x干预为一个足够大的有界区间,即[math][-\frac{L}{2},\frac{L}{2}]^n[/math]上的均匀分布,然后再假设因果机制为一种满足高斯分布的条件概率,其均值为确定值映射[math]f(x)[/math],协方差矩阵为[math]\Sigma[/math],从而在此基础上,再度量因果变量之间的有效信息。这里的因果机制是由映射[math]f(x)[/math]和协方差矩阵共同决定的,也就是条件概率[math]Pr(y|x)[/math]来决定的。
下面,我们将进行更详细地讲解。
Do形式及解释
原始的有效信息是定义在离散的马尔科夫链上的。然而,为了能够更广泛地应用,在这里我们探讨有效信息的更一般的形式。
形式定义
考虑两个随机变量:[math]X[/math]和[math]Y[/math],分别代表因变量(Cause Variable)和果变量(Effect Variable),并且假定它们的取值区间分别是[math]\mathcal{X}[/math]和[math]\mathcal{Y}[/math]。则[math]X[/math]到[math]Y[/math]的有效信息EI的定义为:
[math]\displaystyle{ EI\equiv I(X:Y|do(X\sim U(\mathcal{X})))\equiv I(\tilde{X}:\tilde{Y}) }[/math]
这里,[math]do(X\sim U(\mathcal{X}))[/math]代表对[math]X[/math]实施do干预(或称do操作,英文是do-operator),使其服从[math]\mathcal{X}[/math]上的均匀分布[math]U(\mathcal{X})[/math],也即是最大熵分布。[math]\tilde{X}[/math]与[math]\tilde{Y}[/math]分别代表在经过[math]do[/math]干预后的[math]X[/math]和[math]Y[/math]变量,其中,
[math]\displaystyle{ Pr(\tilde{X}=x)=\frac{1}{\#(\mathcal{X})}, }[/math]
也就是,经过干预后的变量[math]\tilde{X}[/math]与干预前的变量[math]X[/math]之间的最大区别就在于分布不同:[math]\tilde{X}[/math]服从[math]\mathcal{X}[/math]上的均匀分布,而[math]X[/math]则可能是任意的分布。这里[math]\#(\mathcal{X})[/math]代表集合[math]\mathcal{X}[/math]的基数。对于有限元素集合来说,这就是集合中元素的个数。
按照Judea Pearl的理论,do算子实际上是切断了所有指向[math]X[/math]变量的因果箭头,同时保持其它因素,特别是从[math]X[/math]到[math]Y[/math]的因果机制保持不变。所谓的因果机制是指在给定[math]X[/math]取值[math]x\in \mathcal{X}[/math]的情况下,[math]Y[/math]在[math]\mathcal{Y}[/math]上取任意值[math]y\in \mathcal{Y}[/math]的条件概率:
[math]\displaystyle{ f\equiv Pr(Y=y|X=x) }[/math]
在干预中,我们要始终保持则这个因果机制[math]f[/math]保持不变。当没有其它变量影响的时候,这就会导致,[math]Y[/math]的概率分布会跟着发生变化,即被间接干预成为:
[math]\displaystyle{ Pr(\tilde{Y}=y)=\sum_{x\in \mathcal{X}}Pr(X=x) Pr(Y=y|X=x)=\sum_{x\in \mathcal{X}} \frac{Pr(Y=y|X=x)}{\#(\mathcal{X})}. }[/math]
其中,[math]\tilde{Y}[/math]则代表:在保持因果机制[math]f[/math]不变的情况下,[math]Y[/math]变量被[math]X[/math]的do干预所间接改变了的Y变量,这种变化主要体现在概率分布的变化上。
因此,所谓一个因果机制[math]f[/math]的有效信息EI,就是被干预后的因变量[math]\tilde{X}[/math]和果变量[math]\tilde{Y}[/math]之间的互信息。
为什么要使用do算子?
不难看出,尽管EI本质上就是互信息,但是与传统信息论中的互信息不同,有效信息EI在定义中包含了do操作,即对输入变量做了一个干预操作。为什么要引入这一操作呢?
根据Judea Pearl的因果阶梯理论[3],因果推断包含了三个层次,分别是:关联、干预和反事实。阶梯层级越高,因果特征越明显。直接对观测数据估测互信息,便是在度量关联程度;而如果我们能对变量做干预操作,即设定变量为某个值或服从某个分布,便上升到了干预的层级。在EI的定义中引入了[math]do[/math]操作,则使得EI能够比互信息更能体现因果特征。
而从实际意义上来讲,在EI的计算中引入do算子,则可以把数据和动力学分开,从而消除数据分布(即[math]X[/math]的分布)对EI度量所带来的影响。事实上,在一般的因果图上,do算子是一种消除指向被干预变量所有的因果箭头的操作,这种操作可以避免混杂因子造成的虚假关联。因此,EI定义中的do算子也可以消除所有指向因变量[math]X[/math]的因果箭头,包括其它变量(包括不可观测的变量)对[math]X[/math]的影响,从而使得EI更能够刻画动力学本身的特性。
do算子的引入让EI这个指标与其他信息度量指标截然不同,关键在于它是且仅是因果机制的函数,一方面这一特性使得它比其他指标(比如转移熵)更能抓住因果概念的本质,另一方面它需要我们能够已知或获取到因果机制,这在只有观测数据的情况下存在一定的困难。
为什么干预成均匀分布?
在Erik Hoel的原始定义中,do操作是将因变量[math]X[/math]干预成了在其定义域[math]\mathcal{X}[/math]上的均匀分布(也就是最大熵分布)[2][10]。那么, 为什么要干预成均匀分布呢?其它分布是否也可以?
首先,根据上一小节的论述,do操作的实质是希望让EI能够更清晰地刻画因果机制[math]f[/math]的性质,因此,需要切断因变量[math]X[/math]与其它变量的联系,并改变其分布,让EI度量与[math]X[/math]的分布无关。
而之所以要把输入变量干预为均匀分布,其实就是要更好地刻画因果机制的特性。
这是因为,当[math]\mathcal{X}[/math]和[math]\mathcal{Y}[/math]都是有限可数集合的时候,因果机制[math]f\equiv Pr(Y=y|X=x)[/math]就成为了一个[math]\#(\mathcal{X})[/math]行[math]\#(\mathcal{Y})[/math]列的矩阵,我们可以展开EI的定义:
-
[math]\displaystyle{ \begin{aligned} EI &= I(X,Y|do(X\sim U))= \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}Pr(X=x,Y=y)\log \frac{Pr(X=x,Y=y)}{Pr(X=x)Pr(Y=y)}\\ &= \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}Pr(X=x)Pr(Y=y|X=x)\log \frac{Pr(Y=y|X=x)}{Pr(Y=y)}\\ &= \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}Pr(X=x)Pr(Y=y|X=x)\log Pr(Y=y|X=x)- \sum_{x\in\mathcal{X}}\sum_{y\in\mathcal{Y}}Pr(X=x)Pr(Y=y|X=x)\log Pr(Y=y) \\ &=\frac{1}{\#(\mathcal{X})}\left(-\sum_{x\in\mathcal{X}}H(Pr(Y|X))\right) + H(Pr(Y)) \end{aligned} }[/math]
(1)
不难看出,最后得到的等式告诉我们,EI实际上由两项构成,第一项是因果机制矩阵每一行的负熵的平均值,第二项则是变量[math]Y[/math]的熵。 在第一项中,[math]X[/math]的概率分布[math]Pr(X=x)[/math]实际上起到了对每一行的熵求平均时候的权重的作用。只有当我们将该权重取为同样的数值的时候,才能够平等地对待因果机制矩阵中的每一个行,这时就恰好是将[math]X[/math]干预成均匀分布的时候。
如果不是均匀分布,也就意味着某些行的熵就会被乘以一个较大的权重,有的行就会被赋予一个较小的权重,这种权重代表了某种“偏见”,因此也就不能做到让EI能够反映因果机制的天然属性了。
作为分布差异的有效信息
在文献[11]中,作者用另一种方式定义了有效信息。这种新形式的有效信息依赖于果变量(Y)的状态,即干预[math]X[/math]为均匀分布以后的[math]\tilde{Y}[/math]的状态为给定的值[math]Y_0[/math]。在这一条件下,有效信息定义为两种分布的KL散度,这两种概率分布分别是因变量[math]X[/math]的先验分布,即[math]\mathcal{X}[/math]上的均匀分布[math]U[/math],以及在从X到Y的因果机制f的作用下,导致果变量[math]Y[/math]变成了另一个变量[math]\tilde{Y}[/math],那么以观察到这一果变量[math]Y[/math]取值为[math]Y_0[/math]为条件,我们可以反过来推断出因变量[math]\tilde{X}[/math]的后验分布,即[math]P(\tilde{X}|\tilde{Y}=Y_0,f)[/math]。
那么,这种先验的概率分布和后验的概率分布就会产生一个差异,这个差异就是由因果机制f产生的有效信息,可以定义为:
[math]\displaystyle{ ei(f,Y_0)=-D_{KL}(U||P(\tilde{X}|\tilde{Y}=Y_0,f) }[/math]
这里,[math]\tilde{X}[/math]和[math]\tilde{Y}[/math]分别表示将[math]X[/math]干预成均匀分布后(即先验分布),在因果机制[math]f[/math]保持不变的前提下的因变量和果变量。由于KL散度是区分方向的,因此为了保证结果为正,则定义中加上了负号。如果采用其它有关概率分布距离的对称性度量,例如推土距离等,则可以去掉负号。
事实上,[math]ei(f,Y_0)[/math]是某一个[math]Y_0[/math]取值下的有效信息值,如果我们对所有的[math]Y_0[/math]求平均,则可以得到通常意义下的有效信息,即1式。要理解这一点,首先我们需要引入贝叶斯公式,即:
[math]\displaystyle{ P(\tilde{X}|\tilde{Y}=Y_0,f)=\frac{P(\tilde{X},\tilde{Y_0})}{P(\tilde{Y_0})}=\frac{P(\tilde{X_0})P(\tilde{Y_0}|\tilde{X})}{P(\tilde{Y_0})}=\frac{P(\tilde{Y_0}|\tilde{X})}{N\cdot P(\tilde{Y_0})} }[/math]
这里的[math]\tilde{Y_0}\equiv (\tilde{Y}=Y_0)[/math] 注意,这里的条件概率[math]P(\tilde{Y_0}|\tilde{X})[/math]事实上就是因果机制[math]f[/math],进一步,把它代入[math]ei(f,Y_0)[/math]的公式,我们不难得到:
[math]\displaystyle{ ei(f,Y_0)=-D_{KL}(U||P(\tilde{X}|\tilde{Y}=Y_0,f)=\frac{1}{N}\sum_{\tilde{X}}\log\frac{P(\tilde{Y_0}|\tilde{X})}{P(\tilde{Y_0})} }[/math]
将上式对所有的[math]\tilde{Y_0}[/math]值求期望,可以得到:
[math]\displaystyle{ EI=\frac{1}{N}\sum_{\tilde{X},\tilde{Y_0}}P(\tilde{Y_0}|\tilde{X})\log\frac{P(\tilde{Y_0}|\tilde{X})}{P(\tilde{Y_0})} }[/math]
对于[math]ei[/math]的引入,有助于我们理解某一个局部的因果机制是如何改变原始变量的分布的,或者用Tononi的语言来说,这是一种机制的信息产生,详见文章[11]或整合信息论。
马尔科夫链的有效信息
马尔科夫链简介
在本小节中,所有的马尔科夫转移概率矩阵都表示为[math]P[/math]。N为总的状态数量。
最早,Erik Hoel等人是在离散状态的马尔科夫动力学,即马尔科夫链上提出有效信息这一度量因果性的指标的。因此,这一节中,我们介绍有效信息在马尔科夫链上的特殊形式。
所谓的马尔科夫链是指状态离散、时间离散的一种平稳随机过程,它的动力学一般都可以用所谓的转移概率矩阵(Transitional Probability Matrix),简称TPM来表示,有时也叫做概率转移矩阵或状态概率转移矩阵或状态转移矩阵。
具体来讲,马尔科夫链包含一组随机变量[math]X_t[/math],它在状态空间[math]\mathcal{X}=\{1,2,\cdots,N\}[/math]上取值,其中[math]t[/math]往往表示时间。所谓的转移概率矩阵是指一个概率矩阵,其中第[math]i[/math]行,第[math]j[/math]列元素:[math]p_{ij}[/math]表示了系统在任意时刻[math]t[/math]在[math]i[/math]状态的条件下,在[math]t+1[/math]时刻跳转到[math]j[/math]状态的概率。同时,每一行满足归一化条件:
[math]\displaystyle{ \sum_{j=1}^Np_{ij}=1, }[/math]
状态转移矩阵可以看作是马尔科夫链的动力学,这是因为,任意时刻[math]t+1[/math]上的状态概率分布,即[math]Pr(X_t)[/math],可以被上一时刻的状态概率分布,即[math]Pr(X_t)[/math]和状态转移矩阵所唯一确定,并满足关系:
[math]\displaystyle{ Pr(X_{t+1}=j)=\sum_{i=1}^N p_{ij}\cdot Pr(X_t=i), }[/math]
这里的[math]i,j\in \mathcal{X}[/math]都是[math]\mathcal{X}[/math]中的任意状态,且[math]N=\#(\mathcal{X})[/math]即[math]\mathcal{X}[/math]中的总状态数。
下表展示的是三个不同的转移概率矩阵,以及它们的EI数值:
| [math]\displaystyle{ P_1=\begin{pmatrix} &0 &0 &1 &0& \\ &1 &0 &0 &0& \\ &0 &0 &0 &1& \\ &0 &1 &0 &0& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_2=\begin{pmatrix} &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &0 &0 &0 &1& \\ &0 &0 &0 &1& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_3=\begin{pmatrix} &1/4 &1/4 &1/4 &1/4& \\ &1/4 &1/4 &1/4 &1/4& \\ &1/4 &1/4 &1/4 &1/4& \\ &1/4 &1/4 &1/4 &1/4& \\ \end{pmatrix} }[/math]. |
| [math]EI(P_1)=2[/math] bits | [math]EI(P_2)=1[/math] bits | [math]EI(P_3)=0[/math] bits |
这三个马尔科夫链的状态空间都是[math]\mathcal{X}=\{1,2,3,4\}[/math],因此它们的TPM的大小都是[math]4\times 4[/math]。
马尔科夫链的EI
在马尔科夫链中,任意时刻的状态变量[math]X_t[/math]都可以看作是原因,而下一时刻的状态变量[math]X_{t+1}[/math]就可以看作是结果,这样马尔科夫链的状态转移矩阵就是它的因果机制。因此,我们可以将有效信息的定义套用到马尔科夫链上来。
[math]\displaystyle{
\begin{aligned}
EI &= I(X_t,X_{t+1}|do(X_t\sim U(\mathcal{X})))=I(\tilde{X}_t,\tilde{X}_{t+1}) \\
&= \sum^N_{i=1}\sum^N_{j=1}Pr(\tilde{X}_t=i,\tilde{X}_{t+1}=j)\log \frac{Pr(\tilde{X}_t=i,\tilde{X}_{t+1}=j)}{Pr(\tilde{X}_t=i)Pr(\tilde{X}_{t+1}=j)}\\
&= \sum^N_{i=1}Pr(\tilde{X}_t=i)\sum^N_{j=1}Pr(\tilde{X}_{t+1}=j|\tilde{X}_t=i)\log \frac{Pr(\tilde{X}_{t+1}=j|\tilde{X}_t=i)}{Pr(\tilde{X}_{t+1}=j)}\\
&= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{N\cdot p_{ij}}{\sum_{k=1}^N p_{kj}}
\end{aligned}
}[/math]
其中[math]\displaystyle{ \tilde{X}_t,\tilde{X}_{t+1} }[/math]分别为把t时刻的[math]X_t[/math]干预为均匀分布后,前后两个时刻的状态。[math]\displaystyle{ p_{ij} }[/math]为第i个状态转移到第j个状态的转移概率。从这个式子,不难看出,EI仅仅是概率转移矩阵[math]P[/math]的函数。
马尔科夫链EI的向量形式
我们也可以将转移概率矩阵[math]P[/math]写成[math]N[/math]个行向量拼接而成的形式,即:
[math]\displaystyle{ P=(P_1^T,P_2^T,\cdots,P_N^T)^T }[/math]
其中,[math]P_i[/math]矩阵[math]P[/math]的第[math]i[/math]个行向量,且满足条件概率的归一化条件:[math]||P_i||_1=1[/math],这里的[math]||\cdot||_1[/math]表示向量的1范数。那么EI可以写成如下的形式:
-
[math]\displaystyle{ \begin{aligned} EI &= \frac{1}{N}\sum^N_{i=1}\sum^N_{j=1}p_{ij}\log\frac{N\cdot p_{ij}}{\sum_{k=1}^N p_{kj}}\\ &=\frac{1}{N}\cdot \sum_{i=1}^N\left(P_i\cdot \log P_i - P_i\cdot\log \bar{P}\right)\\ &=\frac{1}{N}\sum_{i=1}^N D_{KL}(P_i||\bar{P}) \end{aligned} }[/math]
(2)
将矩阵每列求均值,可得到平均转移向量[math]\displaystyle{ \overline{P}=\sum_{k=1}^N P_k/N }[/math]。[math]D_{KL}[/math]便是两个分布的KL散度。因此,EI是转移矩阵每个行转移向量[math]P_i[/math]与平均转移向量[math]\bar{P}[/math]的KL散度的均值。
针对上面所列的三个状态转移矩阵,我们可以分别求出它们的EI为:2比特、1比特和0比特。由此可见,如果转移概率矩阵中出现更多的0或1,也就是行向量多是独热向量(也叫做one-hot向量,即某一个位置为1,其它位置为0的向量),则EI值就会更大。也就是说,如果在状态转移的过程中,从某一时刻到下一时刻的跳转越确定,则EI值就会倾向于越高。但是,这个观察并不十分精确,更精确的结论由后面的小节给出。
归一化
显然,EI的大小和状态空间大小有关,这一性质在我们比较不同尺度的马尔科夫链的时候非常不方便,我们需要一个尽可能不受尺度效应影响的因果效应度量。因此,我们需要对有效信息EI做一个归一化处理,得到和系统尺寸无关的一个量化指标。
根据Erik Hoel和Tononi等人的工作,要用均匀分布即最大熵分布下的熵值,即[math]\displaystyle{ \log N }[/math]来做分母对EI进行归一化,这里的[math]N[/math]为状态空间[math]\mathcal{X}[/math]中的状态的数量[2]。那么归一化后的EI便等于:
[math]\displaystyle{ Eff=\frac{EI}{\log N} }[/math]
进一步定义归一化指标也称为有效性(effectiveness)。
然而,在处理连续状态变量的时候,这种使用状态空间中状态数量的对数值进行归一化的处理方式并不是非常合适,因为这一状态数往往受到变量的维度和实数分辨率的影响。
确定性和简并性
EI的分解
根据公式1,我们发现,EI实际上可以被分解为两项,即:
[math]\displaystyle{ \begin{aligned} EI&=\frac{1}{\#(\mathcal{X})} \left(-\sum_{x\in\mathcal{X}}H(Pr(Y|X))\right) + H\left(Pr(Y)\right)\\ \end{aligned} }[/math]
同样,在马尔科夫链的情景下,EI也可以做这样的分解:
-
[math]\displaystyle{ \begin{aligned} EI &= \frac{1}{N}\cdot \sum_{i=1}^N\left(P_i\cdot \log P_i - P_i\cdot\log \bar{P}\right)\\ &=\underbrace{-\langle H(P_i)\rangle}_{确定性项}+\underbrace{H(\bar{P})}_{非简并性项} \end{aligned} }[/math]
(tow_terms)
其中,第一项:[math]-\langle H(P_i)\rangle\equiv \frac{1}{N}\sum_{i=1}^N H(P_i)[/math]为每个行向量[math]P_i[/math]的负熵的平均值,它刻画了整个马尔科夫转移矩阵的确定性(determinism);
第二项:[math]H(\bar{P})[/math]为平均行向量的熵,其中[math]\bar{P}\equiv \frac{1}{N}\sum_{i=1}^N P_i [/math]为所有N个行向量的平均行向量,它刻画了整个马尔科夫转移矩阵的非简并性或非退化性(non-degeneracy)。
确定性与简并性
然而上述定义中的确定性项和非简并性都是负数,为此,我们重新定义一个马尔科夫链转移矩阵P的确定性为:
[math]\displaystyle{ Determinism \equiv \log N - \langle H(P_i)\rangle = \frac{1}{N}\sum_{i=1}^N \sum_{j=1}^N p_{ij}\log \left(N\cdot p_{ij}\right) }[/math]
这一项是一个平均的负熵,为了防止其为负数,所以加上了[math]\log N[/math][2]。Determinism能刻画整个转移矩阵的确定性:也就是说如果我们知道了系统当前时刻所处的状态,则我们能够推断出系统在下一时刻所处的状态的程度。为什么这么说呢?这是因为确定性这一项是所有行向量熵的平均值,再取一个负号。我们知道,当一个向量更靠近均匀分布的时候,它的熵就越大,相反,如果一个向量越靠近一个“独热”(one-hot)的向量,也就是这个向量中只有一个1,其它元素都是0,那么它的熵就越小。我们知道,马尔科夫概率转移矩阵的一个行向量的含义就代表系统从当前状态转移到各个不同状态的概率大小。那么,当平均的行向量负熵大的时候,也就是这个行向量的某一个单元概率为1,其它为0,这就意味着系统能够确定地转移到1对应的状态。
我们定义一个马尔科夫链转移矩阵P的简并性为:
[math]\displaystyle{ Degeneracy \equiv \log N - H(\bar{P})=\log N + \sum_{j=1}^N \bar{P}_{\cdot j}\log \bar{P}_{\cdot j}=\sum_{j=1}^N \frac{\sum_{i=1}^Np_{ij}}{N}\log \left(\sum_{i=1}^Np_{ij}\right) }[/math]
这一项为简并性或叫退化性,为了防止其为负数,所以加上了[math]\log N[/math][2]。这里的“简并性”的含义是:如果知道了系统的当前状态,能不能反推系统在上一时刻的状态的能力,如果可以推断,则这个马尔科夫矩阵的简并性就会比较低,也就是非简并的;而如果很难推断,则马尔科夫矩阵就是简并的,也即退化的。为什么“简并性”可以用平均行向量分布的负熵来刻画呢?这是因为,首先,当所有的P中的行向量都是彼此独立的独热向量,那么它们的平均分布就会非常接近于一个均匀分布,即[math]\bar{P}\approx (\frac{1}{N},\frac{1}{N},\cdots,\frac{1}{N})[/math],这个时候,它的Shannon熵最大,即[math]\log N[/math]。而在此时,这个马尔科夫转移矩阵是一个可逆矩阵(由彼此独立的“独热”向量形成的全体彼此线性无关,因此矩阵满秩,因此是可逆的)。这也就意味着,我们从系统当前的状态,是可以推断出系统的上一时刻的状态的,所以这个马尔科夫转移矩阵是非简并的,计算出的简并度恰恰也为0;
其次,当P中的行向量都是相同的独热向量的时候,则平均向量也是一个独热的向量,而这种向量的熵是最小的。在此时,由于所有的上一时刻状态都会转移到行向量中1对应的状态,因此我们也就很难推断出当前这个状态是由哪一个上一步的状态转移过来的。因此,这种情形下的马尔科夫矩阵是简并的(或退化的),计算出来的简并度则恰恰是[math]\log N[/math]。
对于更一般的情况,如果P中的行向量靠近一个彼此独立的独热行向量构成的矩阵,则P就越非简并,相反,如果行向量彼此相同且靠近同一个独热向量,则P就越简并。
举例
下面,我们以三个马尔科夫链为例,来考察它们的确定性和简并性
| [math]\displaystyle{ P_1=\begin{pmatrix} &0 &0 &1 &0& \\ &1 &0 &0 &0& \\ &0 &0 &0 &1& \\ &0 &1 &0 &0& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_2=\begin{pmatrix} &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &0 &0 &0 &1& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_3=\begin{pmatrix} &0 &0 &1 &0& \\ &1 &0 &0 &0& \\ &1 &0 &0 &0& \\ &1 &0 &0 &0& \\ \end{pmatrix} }[/math]. |
| [math]\begin{aligned}&Det(P_1)=2\ bits,\\&Deg(P_1)=0\ bits,\\&EI(P_1)=2\ bits\end{aligned}[/math] | [math]\begin{aligned}&Det(P_2)=0.81\ bits,\\&Deg(P_2)=0\ bits,\\&EI(P_2)=0.81\ bits\end{aligned}[/math] | [math]\begin{aligned}&Det(P_3)=2\ bits,\\&Deg(P_3)=1.19\ bits,\\&EI(P_3)=0.81\ bits\end{aligned}[/math] |
第一个转移概率矩阵是一个置换排列矩阵(Permutation),它是可逆的,因此确定性最高,没有简并性,因而EI最大;第二个矩阵的前三个状态都会以1/3的概率跳转到彼此,因此确定性程度最低,而非简并,EI是0.81;第三个矩阵虽然也是确定性的矩阵,因而确定性最高,但是由于后三个状态都跳转到1,因此,从1状态不能推知它来自于哪个状态,因此简并性最高,最终的EI与第二个相同,仍然是0.81。
归一化的确定性与简并性
在Erik Hoel等人的原始论文中[2],作者们定义的确定性和简并性是以归一化的形式呈现的,也就是将确定性和简并性除以了一个与系统尺度有关的量。为了区分,我们将归一化的对应量称为确定性系数和简并性系数。
具体地,Erik Hoel等人将归一化后的有效信息,即Eff进行分解,分别对应确定性系数(determinism coefficient)和简并性系数(degeneracy coefficient)。
[math]\displaystyle{ Eff = Determinism\ Coefficient - Degeneracy\ Coefficient }[/math]
这两项的定义分别是:
[math]\displaystyle{ \begin{aligned} &Determinism\ Coefficient = \frac{1}{N\log N}\sum_{i,j}p_{ij}\log\left(N\cdot {p_{ij}}\right) \\ &Degeneracy\ Coefficient = \frac{1}{N\log N}\sum_{ij}p_{ij}\log{\left(\sum_k p_{k,j}\right)} \end{aligned} }[/math]
总之,确定性指的是,已知当前时刻状态概率分布,对未来可能状态的判断有多大的把握;而简并性指的是,已知当前的状态,追溯历史,我们能有多大确定性做出判断。如果有状态在动力学过程中发生简并,我们回溯历史时能运用的信息就会变少。当一个系统背后的动力学确定性高,同时简并性低时,说明这是一个具有明显因果效应的动力学。
EI的函数性质
由公式2可以看出,在概率转移矩阵P上,EI是关于矩阵中每一个元素(从某一状态到另一状态的条件概率)的函数,于是我们自然会问:这样一个函数具有哪些数学性质?如它有没有极值点?极值点在哪里?凸性如何?最大值和最小值又是多少?
定义域
在离散状态和离散时间的马尔科夫链上,EI的定义域显然是概率转移矩阵P。P是一个由[math]N\times N[/math]个元素构成的矩阵,其中每一个元素[math]p_{ij}\in[0,1][/math]代表一个概率值,同时对于任意的行,这组概率值需要满足归一化条件,也就是对于任意的[math]\forall i\in[1,N][/math]:
-
[math]\displaystyle{ ||P_i||_1=\sum_{j=1}^N p_{ij}=1 }[/math]
(3)
因此EI的定义域,也就是P的可能空间并不是全部[math]N\times N[/math]维的实数空间[math]\mathcal{R}^{N^2}[/math],由于归一化条件3的存在,使得该定义域成为一个[math]N\times N[/math]维实数空间中的一个子空间。如何表达这个子空间呢?
首先,对于任意一个行向量[math]P_i[/math]来说,它的取值范围空间为N维实数空间中的一个超正多面体。例如,当[math]N=2[/math]的时候,该空间为一条直线:[math]p_{i,1}+p_{i,2}=1, \forall i\in\{1,2\}[/math]。当[math]N=3[/math]的时候,该空间为一张三维空间中的平面:[math]p_{i,1}+p_{i,2}+p_{i,3}=1, \forall i\in\{1,2,3\}[/math]。这两个空间如下图所示:
在一般情况,我们将N维空间下的行向量[math]P_i[/math]的取值范围空间定义为[math]\Delta=\{p_{j}|\sum_{j=1}^Np_{j}=1,p_{j}\in[0,1]\}[/math],则N个这样的空间的笛卡尔积即为EI的定义域:
[math]\displaystyle{ Dom(EI)=\Delta\times \Delta\cdots\times\Delta=\Delta^N }[/math]
一阶导数及极值点
对公式2求[math]p_{ij}[/math]的一阶导数,并注意到归一化条件[math]\sum_{j=1}^Np_{ij}=1[/math],则就可以得到:
-
[math]\displaystyle{ \frac{\partial EI}{\partial p_{ij}}=\log\left(\frac{p_{ij}}{p_{iN}}\right)-\log\left(\frac{\bar{p}_{\cdot j}}{\bar{p}_{\cdot N}}\right), }[/math]
(3)
其中,[math]\displaystyle{ p_{ij} }[/math]表示P中第i行第j列的条件概率,因为P每一行有归一化约束条件2,所以EI函数本身有[math]\displaystyle{ N(N-1) }[/math]个自由变元,我们可以取[math]\displaystyle{ 1\leq i\leq N, 1\leq j\leq N-1 }[/math]。[math]\displaystyle{ p_{iN} }[/math]表示第i行第N列的条件概率,[math]\displaystyle{ \bar{p}_{\cdot j}, \bar{p}_{\cdot N} }[/math]则分别表示第j列和第N列条件概率的均值。不难看出,该导数有定义的前提是对于选定的[math]i,j\in[1,N][/math],[math]p_{ij},p_{iN},\bar{p}_{\cdot j}\equiv \frac{\sum_{k=1}^Np_{kj}}{N},\bar{p}_{\cdot N}\equiv \frac{\sum_{k=1}^Np_{kN}}{N}[/math]都大于0,只有满足这个条件,则EI在[math]p_{ij}[/math]附近是可导的。否则,如果有一项为0,则导数不存在。
令式3等于0,可以求得极值点:即对于任意的[math]\displaystyle{ 1\leq i\leq N, 1\leq j\leq N-1 }[/math],都有下式的成立,
[math]\displaystyle{ p_{ij}=\bar{p}_{\cdot j}=\frac{1}{N}\sum_{k=1}^Np_{kj} }[/math]
不难计算出,此时[math]\displaystyle{ EI=0 }[/math],即EI达到了极值点。根据EI的二阶导数不难判断出,这是极小值点。换个角度来看这个公式,这意味着EI的极小值点有很多个,只要转移概率矩阵所有行向量完全一致,无论该行向量本身是怎样的分布,EI都会等于0。
二阶导数与凸性
进一步地,为了求得EI函数的凸性,我们可以求出EI这个函数的二阶导数[math]\displaystyle{ \frac{\partial^2 EI}{\partial p_{ij}\partial p_{st}} }[/math],其中[math]\displaystyle{ 1\leq s \leq N, 1\leq t \leq N-1 }[/math]。首先我们需要引入一个函数符号[math]\displaystyle{ \delta_{i,j} }[/math],
[math]\displaystyle{ \delta_{i,j} = \begin{cases} 0 & \text{if } i\ne j,\\ 1 & \text{if } i = j. \end{cases} }[/math]
于是我们可以来推导EI的二阶导数,当[math]\displaystyle{ i=s }[/math]时,
[math]\displaystyle{ \begin{equation} \begin{aligned} \frac{\partial^2 EI}{\partial p_{ij}\partial p_{it}}&=\frac{\delta_{j,t}}{N}\left(\frac{1}{p_{ij}}-\frac{1}{N\cdot \bar{p}_{\cdot j}}\right)+\frac{1}{N\cdot p_{iN}}-\frac{1}{N^2\cdot \bar{p}_{\cdot N}}\\ &=\delta_{j,t}\frac{\sum_{k=1}^{N-1}p_{k j}-p_{ij}}{N^2\cdot p_{ij}\cdot \bar{p}_{\cdot j}}+\frac{\sum_{k=1}^{N-1}p_{k N}-p_{iN}}{N^2\cdot p_{iN}\cdot \bar{p}_{\cdot N}}\\ &=\delta_{j,t}\frac{\sum_{k\neq i}p_{kj}}{N^2\cdot p_{ij}\cdot \bar{p}_{\cdot j}}+\frac{\sum_{k\neq i}p_{k N}}{N^2\cdot p_{iN}\cdot \bar{p}_{\cdot N}}\gt 0, \end{aligned} \end{equation} }[/math]
当[math]\displaystyle{ i\ne s }[/math]时,
[math]\displaystyle{ \begin{equation} \frac{\partial^2 EI}{\partial p_{ij}\partial p_{st}}=-\frac{\delta_{j,t}}{N^2\cdot \bar{p}_{\cdot j}}-\frac{1}{N^2\cdot \bar{p}_{\cdot N}}\lt 0. \end{equation} }[/math]
综上,EI的二阶导数为,
[math]\displaystyle{ \begin{equation} \frac{\partial^2 EI}{\partial p_{ij}\partial p_{st}}=\frac{1}{N}\cdot\left(\frac{\delta_{i,s}\delta_{j,t}}{p_{ij}}+\frac{\delta_{i,s}}{p_{iN}}-\frac{\delta_{j,t}}{N\cdot\bar{p}_{\cdot j}}-\frac{1}{N\cdot \bar{p}_{\cdot N}}\right). \end{equation} }[/math]
并且,二阶导数在[math]\displaystyle{ i=s }[/math]的时候为正,在[math]\displaystyle{ i\ne s }[/math]时为负。因此EI既不是凸的也不是凹的。
最小值
前面已经根据EI的一阶导数讨论了它的极值问题。即EI会在所有行向量都是同一个向量的时候达到极小值0。那么,这个极小值是不是最小的呢?
我们知道,根据公式2,EI本质上是一种KL散度,而KL散度都是非负的,也就是说:
[math]\displaystyle{ EI\geq 0 }[/math]
这个不等式的等号在[math]p_{ij}=\bar{p}_{\cdot j}[/math]对所有的[math]i,j[/math]都成立的时候能够取到。因此,0是EI的最小值,且[math]p_{ij}=\bar{p}_{\cdot j}=\frac{1}{N}\sum_{k=1}^Np_{kj}[/math]是它的最小值点,即:
[math]\displaystyle{ EI_{min}=0. }[/math]
最大值
通过前面确定性和简并性章节的讨论,我们知道EI可以拆成两部分,
[math]\displaystyle{ EI = -\langle H(P_i)\rangle + H(\bar{P}), }[/math]
其中熵的定义是[math]\displaystyle{ H(P_i)=-\sum_{j=1}^Np_{ij}\log p_{ij} }[/math]。分开来看,前一项式子最大值为0,即:
[math]\displaystyle{ - H(P_i)\leq 0, }[/math]
当[math]\displaystyle{ P_i }[/math]为没有不确定性的独热向量时,该式子的等号成立。所以,当对所有的i都有[math]\displaystyle{ P_i }[/math]为独热变量时,有
[math]\displaystyle{ -\langle H(P_i)\rangle=0 }[/math]
成立。另一边,P中所有行向量的平均向量的熵也有一个不等式成立,
[math]\displaystyle{ H(\bar{P})\leq \log N, }[/math]
其中等于号在满足[math]\displaystyle{ \bar{P}=\frac{1}{N}\cdot \mathbb{1} }[/math]条件时成立,这里[math]\displaystyle{ \mathbb{1} }[/math]表示全为1的向量。
[math]\displaystyle{ EI\leq 0+\log N=\log N }[/math]
当这两个式子的等号同时成立时,即[math]\displaystyle{ P_i }[/math]为独热向量,同时[math]\displaystyle{ \bar{P} }[/math]为均匀分布时(此时必然要求[math]P_i[/math]彼此垂直,也就是P是一个排列置换矩阵),EI会达到最大值:
[math]\displaystyle{ EI_{max}=\log N }[/math]
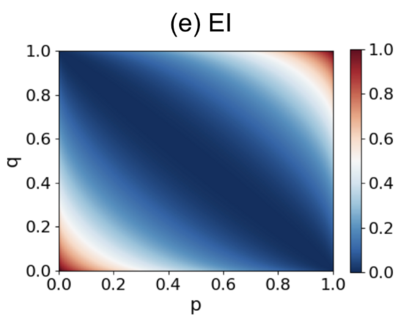
最简马尔科夫链下的解析解
我们考虑一个最简单的2*2马尔科夫链矩阵:
[math]\displaystyle{ P=\begin{pmatrix}p & 1-p \\1-q & q\end{pmatrix}, }[/math]
其中 [math]p[/math] 和 [math]q[/math] 为取值 [math][0,1][/math] 的参数。
这个参数为[math]p[/math]和[math]q[/math]的转移概率矩阵的EI可以通过以下解析解计算:
[math]\displaystyle{ EI=\frac{1}{2}\left[p\log_2\frac{2p}{1+p-q}+(1-p)\log_2\frac{2(1-p)}{1-p+q}\right. + \left.(1-q)\log_2\frac{2(1-q)}{1+p-q}+q\log_2\frac{2q}{1-p+q}\right] }[/math]
下图展示了不同[math]p[/math] 和 [math]q[/math]取值的 EI 的变化。
由这张图不难看出,当p+q=1的时候,也就是所有行向量都相同的情形,EI取得最小值0。否则,随着p,q沿着垂直于p+q=1的方向增大,EI开始变大,而最大值为1.
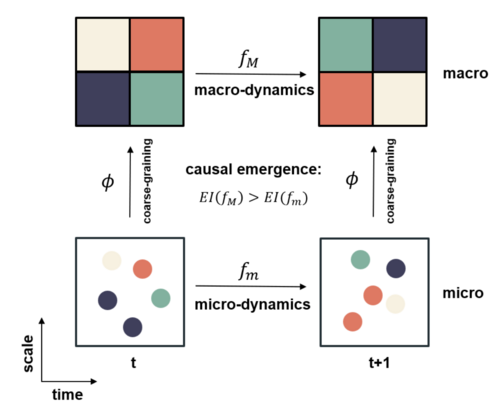
因果涌现
有了有效信息这一度量指标后,我们便可以讨论马尔科夫链上的因果涌现了。对于一个马尔科夫链,观察者可以建立多尺度视角去观测,区分出微观和宏观。首先,原始的马尔科夫概率转移矩阵P即定义了微观动力学;其次,经过对微观态的粗粒化映射(coarse-graining)后(通常反映为对微观状态的分组),观察者可以得到对应的宏观状态(即分组),这些宏观状态彼此之间的概率转移可以用宏观的马尔科夫概率转移矩阵P'来刻画。对两个动力学分别可以计算EI,如果宏观的EI大于微观EI,我们说该系统发生了因果涌现。
可以定义一个新的指标直接度量因果涌现的程度:
[math]\displaystyle{ CE = EI(P') - EI(P) }[/math]
这里[math]P[/math]为微观状态的马尔科夫概率转移矩阵,维度为:[math]N\times N[/math],这里N为微观的状态数;而[math]P'[/math]为对[math]P[/math]做粗粒化操作之后得到的宏观态的马尔科夫概率转移矩阵,维度为[math]M\times M[/math],其中[math]M<N[/math]为宏观状态数。
关于如何对马尔科夫概率转移矩阵实施粗粒化的方法,往往体现为两步:1、对微观状态做归并,将N个微观态,归并为M个宏观态;2、对马尔科夫转移矩阵做约简。关于具体的粗粒化马尔科夫链的方法,请参考马尔科夫链的粗粒化。
如果计算得出的CE>0,则称该系统发生了因果涌现,否则没有发生。
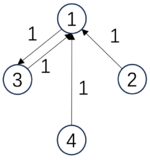
下面,我们展示一个具体的因果涌现的例子:
|
[math]\displaystyle{ P_m=\begin{pmatrix} &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &1/3 &1/3 &1/3 &0& \\ &0 &1 &0 &1& \\ \end{pmatrix} }[/math], |
[math]\displaystyle{ P_M=\begin{pmatrix} &1 &0 & \\ &0 &1 & \\ \end{pmatrix} }[/math]. |
| [math]\begin{aligned}&Det(P_m)=0.81\ bits,\\&Deg(P_m)=0\ bits,\\&EI(P_m)=0.81\ bits\end{aligned}[/math] | [math]\begin{aligned}&Det(P_M)=1\ bits,\\&Deg(P_M)=0\ bits,\\&EI(P_M)=1\ bits\end{aligned}[/math] |
在这个例子中,微观态的转移矩阵是一个4*4的矩阵,其中前三个状态彼此以1/3的概率相互转移,这导致该转移矩阵具有较小的确定性,因此EI也不是很大为0.81。然而,当我们对该矩阵进行粗粒化,也就是把前三个状态合并为一个状态a,而最后一个状态转变为一个宏观态b。这样所有的原本三个微观态彼此之间的转移就变成了宏观态a到a内部的转移了。因此,转移概率矩阵也就变成了[math]P_M[/math],它的EI为1。在这个例子中,可以计算它的因果涌现度量为:
[math]\displaystyle{ CE=EI(P_M)-EI(P_m)=1-0.81=0.19\ bits }[/math]
即存在着0.19比特的因果涌现。
有时,我们也会根据归一化的EI来计算因果涌现度量,即:
[math]\displaystyle{ ce=Eff(P_M)-Eff(P_m)=1-0.405=0.595 }[/math]
由此可见,由于归一化的EI消除了系统尺寸的影响,因此因果涌现度量更大。
计算EI的源代码
这是计算一个马尔科夫概率转移矩阵的Python源代码。输入tpm为一个满足行归一化条件的马尔科夫概率转移矩阵,返回的ei_all为其EI值,eff为有效性,det,deg分别为确定性和简并性,det_c,deg_c分别为确定性系数和简并性系数。
python:
def tpm_ei(tpm, log_base = 2):
'''
tpm: 输入的概率转移矩阵,可以是非方阵
log_base:对数的底
ei_all:EI的值
det:EI中确定性的部分
deg:EI中简并性的部分
eff:有效性
det_c:确定性系数
deg_c:简并性系数
'''
# marginal distribution of y given x ~ Unifrom Dist
puy = tpm.mean(axis=0)
m,n = tpm.shape
if m > n:
q = n
else:
q = m
# replace 0 to a positive number to avoid log error
eps = 0.5
tpm_e = np.where(tpm==0, eps, tpm)
puy_e = np.where(puy==0, eps, puy)
# calculate EI of specific x
ei_x = (np.log2(tpm_e / puy_e) / np.log2(log_base) * tpm).sum(axis=1)
# calculate det and deg
det = np.log2(n) + (tpm * np.log2(tpm_e)).sum(axis=1).mean(axis=0)
deg = np.log2(n) + (puy * np.log2(puy_e)).sum()
det = det / np.log2(log_base)
deg = deg / np.log2(log_base)
det_c = det / np.log2(q) * np.log2(log_base)
deg_c = deg / np.log2(q) * np.log2(log_base)
# calculate total EI
ei_all = ei_x.mean()
eff = ei_all / np.log2(q) * np.log2(log_base)
return ei_all,det,deg,eff,det_c,deg_c
tpm_ei(mi_states)
连续变量的EI
现实中大部分系统都要在连续空间上考虑,所以很有必要将EI的概念拓展到连续系统上。
这种扩展的核心思想是将连续空间中的因果机制简化为一个确定性的函数映射[math]f(X)[/math]再加上一个噪声随机变量[math]\xi[/math]。而且,在下面列举的情形中,[math]\xi\sim \mathcal{N}(0,\Sigma)[/math],即满足高斯分布,这样便可求得EI的解析表达式。对于更一般的情况,尚没有文献进行讨论。
随机函数映射
最初Erik Hoel考虑到了这一点,提出了因果几何[4]框架,它不仅率先讨论了随机函数映射的EI计算问题,同时还引入了干预噪音和因果几何的概念,并定义了EI的局部形式,并将这种形式与信息几何进行了对照和类比。下面,我们分别从一维函数映射、多维函数映射,和EI的局部形式来分别进行讨论。
一维函数映射
首先,我们考虑最简单的情况:
[math]\displaystyle{ y=f(x)+\varepsilon, \varepsilon\sim\mathcal{N}(0,\sigma^2) }[/math]
其中,[math]x,y\in \mathcal{R}[/math]都是一维实数变量。按照有效信息的定义,我们需要对变量x进行干预,使其满足在其定义域空间上服从均匀分布。如果x的定义域为一个固定的区间,如[a,b],其中a,b都是实数,那么x的概率密度函数就是[math]1/(b-a)[/math]。然而,当x的定义域为全体实数的时候,区间成为了无穷大,而x的概率密度函数就成为了无穷小。
为了解决这个问题,我们假设x的定义域不是整个实数空间,而是一个足够大的区域:[math][-L/2,L/2][/math],其中L为该区间的大小。这样,该区域上的均匀分布的密度函数为:[math]1/L[/math]。我们希望当[math]L\rightarrow +\infty[/math]的时候,EI能够收敛到一个有限的数。然而,实际的EI是一个和x定义域大小有关的量,所以EI是参数L的函数。这一点可以从EI的定义中看出:
-
[math]\displaystyle{ \begin{aligned} EI&=I(y;x|do(x\sim U[-L/2,L/2]))\\ &=\int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{f([-\frac{L}{2},\frac{L}{2}])}p(x)p(y|x)\ln\frac{p(y|x)}{p(y)}dydx\\ &=\int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{f([-\frac{L}{2},\frac{L}{2}])}p(x)p(y|x)\ln p(y|x)dydx -\int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{f([-\frac{L}{2},\frac{L}{2}])}p(x)p(y|x)\ln p(y)dydx \end{aligned} }[/math]
(4)
这里,[math]p(y|x)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(y-f(x))^2}{\sigma^2}\right)[/math]为给定x的条件下,y的条件概率密度函数。由于[math]\varepsilon[/math]服从均值为0,方差为[math]\sigma^2[/math]的正态分布,所以[math]y=f(x)+\varepsilon[/math]就服从均值为[math]f(x)[/math],方差为[math]\sigma^2[/math]的正态分布。
y的积分区间为:[math]f([-\frac{L}{L},\frac{L}{2}])[/math],即将x的定义域[math][-\frac{L}{2},\frac{L}{2}][/math]经过f的映射,形成y上的区间范围。
[math]\displaystyle{ p(y)=\int_{-\frac{L}{2}}^{\frac{L}{2}}p(x_0)p(y|x_0)dx_0=\int_{-\frac{L}{2}}^{\frac{L}{2}}\frac{1}{L}\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(y-f(x_0))^2}{\sigma^2}\right)dx_0 }[/math]
为y的概率密度函数,它也可以由联合概率密度函数[math]p(x,y)=p(x)p(y|x)[/math]对x进行积分得到。为了后续叙述方便,我们将x重新命名为[math]x_0[/math],从而以区分出现在4中的其它x变量。
由于L很大,所以区间[math][-\frac{L}{2},\frac{L}{2}][/math]很大,进而假设区间[math]f([-\frac{L}{L},\frac{L}{2}])[/math]也很大。这就使得,上述积分的积分上下界可以近似取到无穷大,也就有4中的第一项为:
[math]\displaystyle{ \begin{aligned} \int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{f([-\frac{L}{2},\frac{L}{2}])}p(x)p(y|x)\ln p(y|x)dydx&\approx \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}p(x)p(y|x)\ln p(y|x)dydx\\ &=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\frac{1}{L}\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(y-f(x))^2}{\sigma^2}\right)\ln\left[\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(y-f(x))^2}{\sigma^2}\right)\right]dydx\\ &=\ln(\frac{1}{\sigma\cdot\sqrt{2\pi e}}) \end{aligned} }[/math]
其中,e为自然对数的底,最后一个等式是根据高斯分布函数的Shannon熵公式计算得出的。
然而,要计算第二项,即使使用了积分区间为无穷大这个条件,仍然很难计算得出结果,为此,我们对函数[math]f(x_0)[/math]进行一阶泰勒展开:
[math]\displaystyle{ f(x_0)\approx f(x)+f'(x)(x_0-x) }[/math]
这里,[math]x\in[-\frac{L}{2},\frac{L}{2}][/math]是x定义域上的任意一点。
因此,p(y)可以被近似计算:
[math]\displaystyle{ p(y)=\int_{-\frac{L}{2}}^{\frac{L}{2}}\frac{1}{L}\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(y-f(x_0))^2}{\sigma^2}\right)dx_0\approx \int_{-\infty}^{\infty}\frac{1}{L}\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(y-f(x)-f'(x)(x_0-x))^2}{\sigma^2}\right)dx_0\approx \frac{1}{L}\cdot\frac{1}{f'(x)} }[/math]
值得注意的是,在这一步中,我们不仅将[math]f(x_0)[/math]近似为一个线性函数,同时还引入了一个假设,即p(y)的结果与y无关,而与[math]x[/math]有关。我们知道在对EI计算的第二项中包含着对x的积分,因此这一近似也就意味着不同x处的p(y)近似是不同的。
这样,4中的第二项近似为:
[math]\displaystyle{ \begin{aligned} \int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{f([-\frac{L}{2},\frac{L}{2}])}p(x)p(y|x)\ln p(y)dydx\approx -\ln L - \frac{1}{L}\int_{-\frac{L}{2}}^{\frac{L}{2}}\ln f'(x)dx \end{aligned} }[/math]
最终的EI可以由下式近似计算:
[math]\displaystyle{ EI\approx \ln(\frac{L}{\sqrt{2\pi e}})+\frac{1}{2L}\int_{-\frac{L}{2}}^{\frac{L}{2}}\ln \left(\frac{f'(x)}{\sigma}\right)^2dx }[/math]
与上述推导类似的推导首见于Hoel2013的文章中[2],并在神经信息压缩器一文中[5]中进行了详细讨论。
高维情况
我们可以把上述对一维变量的EI计算推广到更一般的n维情景。即:
-
[math]\displaystyle{ \mathbf{y}=f(\mathbf{x})+\xi, }[/math]
(5)
其中,[math]\xi\sim \mathcal{N}(0,\Sigma)[/math],[math]\displaystyle{ \Sigma }[/math]是高斯噪声[math]\displaystyle{ \xi }[/math]的协方差矩阵。 首先,我们将[math]\mathbf{x}[/math]干预成[math]\displaystyle{ [-L/2,L/2]^n\subset\mathcal{R}^n }[/math]上的均匀分布,[math]\displaystyle{ [-L/2,L/2]^n }[/math]表示n维空间中的超立方体,我们假设[math]\displaystyle{ \mathbf{y}\in\mathcal{R}^m }[/math],其中[math]\displaystyle{ n }[/math]和[math]\displaystyle{ m }[/math]是正整数。只存在观测噪声的情况下,EI可以推广为以下形式:
-
[math]\displaystyle{ EI\approx \ln\left(\frac{L^n}{(2\pi e)^{m/2}}\right)+\frac{1}{L^n}\int_{-[\frac{L}{2},\frac{L}{2}]^n}\ln\left|\det\left(\frac{\partial_\mathbf{x} f(\mathbf{x})}{\Sigma^{1/2}}\right)\right| d\mathbf{x}, }[/math]
(6)
其中,[math]\displaystyle{ |\cdot| }[/math]是绝对值运算,[math]\displaystyle{ \det }[/math]是行列式。
维度平均的EI
在离散状态的系统中,当我们比较不同尺度系统的时候,可以直接计算EI的差异也可以计算归一化的EI差异。归一化的EI是除以[math]\log N[/math],这里[math]N=\#(\mathcal{X})[/math]为离散状态空间[math]\mathcal{X}[/math]中的元素个数。
然而,在针对连续变量进行扩展的时候,如果使用原始的EI,那么就会出现不合理的情况。首先,如公式6所示,EI的计算公式中包含着[math]\ln L^n[/math]项。由于L为一个很大的正数,因而EI的计算结果将会受到L的严重影响。其次,如果计算归一化的EI,即Eff,那么会遇到一个问题是,对于连续变量来说,其状态空间的元素个数为无穷多个,如果直接使用,势必会引入无穷大量。一种解决办法是将空间的体积视作个数N,因此应该除以归一化变量为:[math]n \ln L[/math],由此可见它是正比于n和ln L的,即:
[math]\displaystyle{ Eff=\frac{EI}{\ln L^n}\approx 1-\frac{m\ln\left(2\pi e\right)}{2n \ln L}+\frac{1}{n\ln L}\int_{[-\frac{L}{2},\frac{L}{2}]^n}\frac{1}{L^n}\cdot \ln\left|\det\left(\frac{\partial_\mathbf{x} f(\mathbf{x})}{\Sigma^{1/2}}\right)\right| d\mathbf{x}, }[/math]
然而,在这个式子中,仍然包含着L项,因而也会对Eff造成很大的影响。并且,当我们比较微观(n维)和宏观(m维,且m<n)两个维度的Eff时,即计算归一化的因果涌现的时候,L并不能消掉。
看来,连续变量系统的归一化问题并不能简单平移离散变量的结果。
在神经信息压缩器(Neural information squeezer, NIS)的框架被提出时[5],作者们发明了另一种对连续变量的有效信息进行归一化方式,即用状态空间维数来归一化EI,从而解决连续状态变量上的EI比较问题,这一指标被称为维度平均的有效信息(Dimension Averaged Effective Information,简称dEI)。其描述为:
[math]\displaystyle{ \mathcal{J}\equiv\frac{EI}{n} }[/math]
这里,[math]n[/math]为状态空间的维度。可以证明,在离散的状态空间中,维度平均的EI和有效性指标(Eff)实际上是等价的。关于连续变量上的EI,我们将在下文进一步详述。
对于n维迭代动力系统来说,首先,[math]\mathbf{y}[/math]和[math]\mathbf{x}[/math]是同一维度的变量,因此[math]m=n[/math],因而:将公式6代入维度平均EI,得到:
[math]\displaystyle{ \mathcal{J}=\frac{EI}{n}\approx \ln L - \frac{1}{2}\ln (2\pi e)+\frac{1}{n}\int_{[-\frac{L}{2},\frac{L}{2}]^n}\frac{1}{L^n}\cdot \ln\left|\det\left(\frac{\partial_\mathbf{x} f(\mathbf{x})}{\Sigma^{1/2}}\right)\right| d\mathbf{x} }[/math]
虽然L仍然没有消失,但是当我们计算维度平均的因果涌现的时候,即假设我们可以将n维的状态变量[math]\mathbf{x}_t[/math]投影到一个N维的宏观态变量[math]\mathbf{X}_t[/math],以及相对应的宏观动力学(F),和噪声的协方差[math]\Sigma'[/math]则宏观动力学的维度平均EI与微观动力学的维度平均EI之差为:
[math]\displaystyle{ \Delta \mathcal{J}\equiv \mathcal{J_F}-\mathcal{J_f}=\frac{EI_F}{N}-\frac{EI_f}{n}\approx \frac{1}{N}\int_{-[\frac{L}{2},\frac{L}{2}]^N}\frac{1}{L^N}\cdot \ln \left|\det\left(\frac{\partial_\mathbf{X} F(\mathbf{X})}{\Sigma'^{1/2}}\right)\right| dX - \frac{1}{n}\int_{[-\frac{L}{2},\frac{L}{2}]^n}\frac{1}{L^n}\cdot \ln\left|\det\left(\frac{\partial_\mathbf{x} f(\mathbf{x})}{\Sigma^{1/2}}\right)\right| d\mathbf{x} }[/math]
注意,上式中的积分可以写成均匀分布下的期望,即[math]\int_{[-\frac{L}{2},\frac{L}{2}]}\frac{1}{L^n}\cdot=\mathbb{E}_{\mathbf{x}\sim \mathcal{U}[-\frac{L}{2},\frac{L}{2}]^n}\cdot[/math],继而上式化为:
[math]\displaystyle{
\Delta \mathcal{J}\approx \frac{1}{N}\mathbb{E}_{X\sim\mathcal{U}[-\frac{L}{2},\frac{L}{2}]^N}\ln \left|\det\left(\frac{\partial_\mathbf{X} F(\mathbf{X})}{\Sigma'^{1/2}}\right)\right| - \frac{1}{n}\mathbb{E}_{\mathbf{x}\sim\mathcal{U}[-\frac{L}{2},\frac{L}{2}]^n}\ln\left|\det\left(\frac{\partial_\mathbf{x} f(\mathbf{x})}{\Sigma^{1/2}}\right)\right|
}[/math]
这里[math]\mathcal{U}([-\frac{L}{2},\frac{L}{2}]^n)[/math]表示立方体[math][-\frac{L}{2},\frac{L}{2}]^n[/math]上的均匀分布。由此可见,尽管在期望中仍然隐含地包含L,但该式中所有显含L的项就都被消失了。在实际数值计算的时候,期望的计算可以表现为在[math][-\frac{L}{2},\frac{L}{2}]^n[/math]上多个采样取平均,因而也是与L的大小无关的。这就展示出来引入维度平均EI的一定的合理性。
随机迭代系统
我们可以把上述结论,推广到线性迭代动力系统中[7],也就是对于形如
[math]\displaystyle{ x_{t+1}=Ax_t+\varepsilon_t, }[/math]
的迭代系统,其中,[math]A\in\mathcal{R}^{n\times n}[/math]是尺度为n*n的满秩的方阵,代表线性迭代系统中的动力学系数, [math]\varepsilon_t\sim\mathcal{N}(0,\Sigma)[/math]为n维的高斯噪声,满足0均值,协方差为[math]\Sigma[/math]的正态分布,其中,协方差矩阵[math]\Sigma[/math]也是满秩的。
可以看出这一迭代系统可以看做是公式5的特例,其中[math]y[/math]对应这里的[math]x_{t+1}[/math],[math]f(x_t)[/math]即是[math]A x_t[/math]。
为定义EI,设干预空间大小为[math]\displaystyle{ L }[/math],对于单步的映射我们可以得到维度平均有效信息
[math]\displaystyle{ \mathcal{J}(A,\Sigma)\equiv \frac{EI(A,\Sigma)}{n}=\frac{1}{n}\ln\displaystyle\frac{|\det(A)|L^n}{(2\pi e)^\frac{n}{2}\displaystyle \det(\Sigma)^\frac{1}{2}}=\ln\displaystyle\frac{|\det(A)|^\frac{1}{n}L}{(2\pi e)^\frac{1}{2}\displaystyle \det(\Sigma)^\frac{1}{2n}}. }[/math]
随机迭代系统的有效信息可以分解确定性和简并性为两项,
[math]\displaystyle{ \mathcal{J}=\mathcal{J}_1-\mathcal{J}_2 }[/math]
其中确定性
[math]\displaystyle{ \mathcal{J}_1\equiv-\left\lt H(p(x_{t+1}|x_t))\right\gt =-\ln\left[(2\pi e)^\frac{n}{2}\det(\Sigma)^\frac{1}{2}\right] }[/math]
描述系统前一时刻状态已知的情况下,后一时刻的随机性,确定性越强,随机性越小,越容易对系统未来趋势进行预测;
简并性:
[math]\displaystyle{ \mathcal{J}_2\equiv-H(\tilde{x}_{t+1}))=-\ln\left(|\det(A)|L^n\right) }[/math]
描述后一时刻已知的情况下,对前一时刻的可追溯性,简并性越弱,越容易推断系统以往的演化路径。其中,[math]\tilde{x}_{t+1}[/math]是保持因果机制不变,经过干预以后得到的新的[math]x_{t+1}[/math]变量。
确定性越强,简并性越弱,有效信息则会越大,因果效应越强。
宏观有效信息与微观有效信息做差之后就可以得到随即迭代系统的因果涌现为:
[math]\displaystyle{ \Delta\mathcal{J}=\ln\frac{|\det(WAW^{\dagger})|^{1/N}}{|\det(A)|^{1/n}}-\ln\frac{|\det(W\Sigma W^T)|^{\frac{1}{2N}}}{|\det(\Sigma)|^{\frac{1}{2n}}} }[/math]
其中,[math]W[/math]为粗粒化矩阵,它的阶数为n*m,m为宏观状态空间的维度,它的作用是把任意的微观态[math]x_t[/math]映射为宏观态[math]y_t[/math]。[math]W^{\dagger}[/math]为W的伪逆运算。式中第一项是由确定性引发的涌现,简称确定性涌现(Determinism Emergence),第二项为简并性引发的涌现,简称简并性涌现。更详细的内容参看随机迭代系统的因果涌现。
前馈神经网络
针对复杂系统自动建模任务,我们往往使用神经网络来建模系统动力学。具体的,对于前馈神经网络来说,张江等人推导出了前馈神经网络有效信息的计算公式[5],其中神经网络的输入是[math]\displaystyle{ x(x_1,...,x_n) }[/math],输出是[math]\displaystyle{ y(y_1,...,y_n) }[/math],并且满足[math]\displaystyle{ y=f(x) }[/math],[math]\displaystyle{ f }[/math]是由神经网络实现的确定性映射。然而,根据公式5,映射中必须包含噪声才能够体现不确定性。
因而,在神经网络中,我们假设神经网络从输入到输出的计算也是不确定性的,即也符合公式5:
[math]\displaystyle{ y=f(x)+\xi, }[/math]
这里,[math]\xi\sim \mathcal{N}(0,\Sigma)[/math]为一高斯噪声,且[math]\Sigma=\mathrm{diag}(\sigma_1,\sigma_2,\cdots,\sigma_n)[/math],这里[math]\sigma_i[/math]为第i个维度的最小平方误差(Mean Square Error,简称MSE误差)。也就是说,我们假设从x到y的神经网络映射实际上满足一个均值为[math]f(x)[/math],协方差为[math]\Sigma[/math]的条件高斯分布,即:
[math]\displaystyle{ Pr(y|x)\sim \mathcal{N}(f(x),\Sigma) }[/math]
由此,套用高维映射一般情况下的结论,我们可以给出神经网络有效信息的一般计算公式:
[math]\displaystyle{ \begin{gathered}EI(f)=I(do(x\sim \mathcal{U}([-\frac{L}{2},\frac{L}{2}]^n));y)\approx-\frac{n+n\ln(2\pi)+\sum_{i=1}^n\ln\sigma_i^2}2+n\ln(2L)+\mathbb{E}_{x\sim \mathcal{U}([-\frac{L}{2},\frac{L}{2}]^n)}(\ln|\det(\partial_{x}f(x)))|)\end{gathered} }[/math]
其中[math]\displaystyle{ \mathcal{U}\left(\left[-L/2, L/2\right]^n\right) }[/math]表示范围在[math]\displaystyle{ \left[-L/2 ,L/2\right]^n }[/math]上的[math]\displaystyle{ n }[/math]维均匀分布,[math]\displaystyle{ \det }[/math]表示行列式。维度平均EI为:
[math]\displaystyle{ \begin{gathered} \mathcal{J}\equiv \frac{EI(f)}{n}\approx -\frac{\ln(2\pi e)}{2}-\frac{\sum_{i=1}^n\ln\sigma_i}{n}+\ln(2L)+\frac{1}{n}\cdot\mathbb{E}_{x\sim \mathcal{U}([-\frac{L}{2},\frac{L}{2}]^n)}(\ln|\det(\partial_{x}f(x)))|) \end{gathered} }[/math]
如果设微观的动力学可以用神经网络f来拟合,宏观动力学则可以用F来拟合,则因果涌现可以由下式计算:
[math]\displaystyle{
\begin{gathered}
\mathcal{\Delta J}\equiv \frac{EI(F)}{m}-\frac{EI(f)}{n}\approx \frac{\sum_{i=1}^n\ln\sigma_i}{n}-\frac{\sum_{i=1}^m\ln\sigma'_i}{m}+\frac{1}{m}\cdot\mathbb{E}_{X\sim \mathcal{U}([-\frac{L}{2},\frac{L}{2}]^n)}(\ln|\det(\partial_{X}F(X)))|)-\frac{1}{n}\cdot\mathbb{E}_{x\sim \mathcal{U}([-\frac{L}{2},\frac{L}{2}]^m)}(\ln|\det(\partial_{x}f(x)))|)
\end{gathered}
}[/math]
其中,[math]m[/math]为宏观态维度,[math]\sigma'_i[/math]为第i个宏观维度的平均平方误差(MSE),这一误差可以通过反向传播算法计算的宏观态[math]X_i[/math]的梯度计算得出。
注意,上述结论都要求:[math]\displaystyle{ \partial_{x}f(x) }[/math]不为0,而对于所有的[math]\displaystyle{ x }[/math],[math]\displaystyle{ \partial_{x}f(x) }[/math]处处为0时,我们得到: [math]\displaystyle{ \begin{gathered}EI(f)\approx\end{gathered}0 }[/math]。对于更一般的情形,则需要考虑矩阵不满秩的情况,请参考神经网络的有效信息。
连续系统EI的源代码
可逆神经网络下的数值解以及随机迭代系统的解析解都可以给出计算方法。
对于一般的神经网络,它可看做是从输入X到输出Y的一种不确定的函数映射: [math]\displaystyle{ y=f(x)+\xi }[/math]
其中x的维度为input_size,y的维度为output_size,[math]\xi[/math]为一高斯分布,其协方差矩阵为:[math]\Sigma=\mathrm{diag}(\sigma_1,\sigma_2,\cdots,\sigma_n)[/math],这里,[math]\sigma_i[/math]为该神经网络第i个维度的均方误差(MSE)。该矩阵的逆记为sigmas_matrix。映射函数f记为func,则可以用下面的代码计算该神经网络的EI。该算法的基本思想是利用蒙特卡洛方法计算公式6的积分。
- 输入变量:
神经网络的输入维度(input_size)输出维数(output_size)、输出变量视为高斯分布后的协方差矩阵的逆(sigmas_matrix)、映射函数(func)、干预区间大小(L的取值)、以及蒙特卡罗积分的样本数(num_samples)。
- 输出变量:
维度平均EI(d_EI)、EI系数(eff)、EI值(EI)、确定性(term1)、简并性(term2)和[math]\ln L[/math](-np.log(rho))。
def approx_ei(input_size, output_size, sigmas_matrix, func, num_samples, L, easy=True, device=None):
rho=1/(2*L)**input_size #the density of X even distribution
#the first term of EI, the entropy of a gaussian distribution
#sigmas_matrix_np=sigmas_matrix.cpu() if use_cuda else sigmas_matrix
dett=1.0
if easy:
dd = torch.diag(sigmas_matrix)
dett = torch.log(dd).sum()
else:
#dett = np.log(np.linalg.det(sigmas_matrix_np))
dett = torch.log(torch.linalg.det(sigmas_matrix))
term1 = - (output_size + output_size * np.log(2*np.pi) + dett)/2
#sampling x on the space [-L,L]^n, n is the number of samples
xx=L*2*(torch.rand(num_samples, input_size, device=sigmas_matrix.device)-1/2)
dets = 0
logdets = 0
#iterate all samples of x
for i in range(xx.size()[0]):
jac=jacobian(func, xx[i,:]) #use pytorch's jacobian function to obtain jacobian matrix
det=torch.abs(torch.det(jac)) #calculate the determinate of the jacobian matrix
dets += det.item()
if det!=0:
logdets+=torch.log(det).item() #log jacobian
else:
#if det==0 then, it becomes a gaussian integration
logdet = -(output_size+output_size*np.log(2*np.pi)+dett)
logdets+=logdet.item()
int_jacobian = logdets / xx.size()[0] #take average of log jacobian
term2 = -np.log(rho) + int_jacobian # derive the 2nd term
if dets==0:
term2 = - term1
EI = max(term1 + term2, 0)
if torch.is_tensor(EI):
EI = EI.item()
eff = -EI / np.log(rho)
d_EI = EI/output_size
return d_EI, eff, EI, term1, term2, -np.log(rho)
对于随机迭代系统,由于是解析解,相对会简单许多。既可以直接计算,也可以作为上述神经网络计算结果的对照。输入的变量分别为参数矩阵和协方差矩阵。
def EI_calculate_SIS(A,Sigma):
n=A.shape[0]
return math.log(abs(sl.det(A))/(np.sqrt(sl.det(Sigma))*math.pow(2*np.pi*np.e,n/2)))
EI与其它相关主题
EI与整合信息论
有效信息这一指标最早出现在文献Tononi等人(2003)的文章中[1],在这篇文章中,作者们定义了整合信息能力这一指标,并建立了整合信息理论,这一理论后来演化成意识理论的一个重要分支。而整合信息能力这一指标的定义是以有效信息为基础的。
EI与Φ
整合信息能力(或者叫整合程度)[math]\displaystyle{ \Phi }[/math],可以被定义为系统的任意一个二划分两部分之间相互影响的有效信息最小值。假如系统是X,S是X的一个子集,它被划分为两个部分,分别是A和B。那么,A、B之间以及它们跟X中其余的部分都存在着相互作用和因果关系。
这时,我们可以度量这些因果关系的强弱。首先,我们来计算从A到B的有效信息。即干预A,使其服从最大熵分布,然后度量A和B之间的互信息:
[math]\displaystyle{ EI(A\rightarrow B) = I(A^{H^{max}}: B) }[/math]
这里[math]\displaystyle{ A^{H^{max}} }[/math]表示A上的最大熵分布,也就是前文中的均匀分布。该式子中没有明确表示,但实际上暗含了一种从A到B的因果机制,即[math]Pr(B|A)[/math]。它在干预中始终保持不变。这样,如果A的不同状态会导致B有很不一样的变化,这个EI值会很高;反之,如果无论A怎么变,B都受到很少的影响,那么EI就会很低。显然,这种度量是有方向的,A对B的EI和B对A的EI可以很不同。我们可以把这两个方向的EI加在一起,得到S在某一个划分下的EI大小。
[math]\displaystyle{ EI(A\leftrightarrow B) = EI(A\rightarrow B) + EI(B\rightarrow A) }[/math]
遍历各种划分,如果存在某一个划分S,使得EI为0,说明这个S可以被看做是两个因果独立的部分,所以整合程度也应该是0。从这种特殊例子中我们可以看出,我们应该关注所有划分中有效信息最小的那个。当然,不同划分会导致A和B的状态空间就不一样,所以应该做一个归一化处理,即除以A和B最大熵值中较小的那一个。于是,我们可以有一个最小信息划分(minimum information bipartition,MIB)。整合程度[math]\displaystyle{ \Phi }[/math]定义如下:
[math]\displaystyle{ \Phi(S) = EI(MIB(S)) }[/math]
这就是整合信息能力与有效信息的关系。
区别
值得注意的是,与马尔科夫链的EI计算不同,这里的EI更多衡量的是系统中两个部分彼此之间的因果联系。而马尔科夫链的EI衡量的是同一个系统在不同两个时刻之间的因果关联强度。
EI与其它因果度量指标
EI是一种度量因果机制中因果变量的因果联系强弱的一种指标。而在EI提出之前,已有多个因果度量指标被提出了。那么,EI和这些因果度量指标之间存在着什么样的联系呢?事实上,正如Comolatti与Hoel在2022年的文章中所指出的,包括EI在内的这些因果度量指标都可以统一表达为两个基本要素的组合[12]。这两个基本要素被称为“因果元语”(Causal Primatives),分别代表了因果关系中的充分性和必要性。
因果元语的定义
[math]\displaystyle{ \begin{aligned} \text{充分性:}~~~&suff(e,c) = P(e|c) \\ \text{必要性:}~~~&nec(e,c) = 1 - P(e|C \backslash c) \end{aligned} }[/math]
其中[math]\displaystyle{ c }[/math]和[math]\displaystyle{ e }[/math]分别表示因事件(cause)和果事件(effect),[math]\displaystyle{ C }[/math]表示因事件的全部集合,[math]\displaystyle{ C \backslash c }[/math]则为因事件[math]\displaystyle{ c }[/math]的补集,即[math]\displaystyle{ c }[/math]之外的事件,也可记作[math]\displaystyle{ \lnot c }[/math]。充分性表明当因发生时,果发生的概率,当[math]\displaystyle{ suff = 1 }[/math]时,因发生确定导致果发生;而必要性则衡量当因不发生时,果也不发生的概率;当[math]\displaystyle{ nec = 1 }[/math]时,因不发生则果一定不发生。
有些因果指标中的必要性表现为以下的变型形式,在此也给出定义:
[math]\displaystyle{ \begin{aligned} \text{必要性}' \text{:}~~~nec'(e) = 1 - P(e|C) \end{aligned} }[/math]
根据定义,当[math]\displaystyle{ c }[/math]为极小概率事件时,[math]\displaystyle{ nec(e,c) \approx nec'(e) }[/math]。当[math]\displaystyle{ C }[/math]为连续状态空间时,可认为两者等价。
注意:[math]\displaystyle{ nec'(e) }[/math]的定义与文献[12]中定义的[math]\displaystyle{ nec^\dagger(e) = P(e|C) }[/math]不同,两者关系为[math]\displaystyle{ net'(e) = 1 - nec^\dagger(e) }[/math]。
因果元语与确定性和简并性
如前所述,EI可被分解为确定性与简并性两项,这两项分别对应充分性和必要性的因果元语表达:
[math]\displaystyle{ Determinism\quad Coef= \sum_{e \in E, c \in C}{P(e,c)\cdot \left[1 - \frac{\log{\frac{1}{suff(e,c)}}}{\log{N}}\right]} }[/math]
[math]\displaystyle{ Degeneracy\quad Coef= \sum_{e \in E}{P(e|C)\cdot\left[1 - \frac{\log{\frac{1}{1 - nec'(e)}}}{\log{N}}\right]} }[/math]
可以看到,充分性和确定性之间,以及必要性和简并性之间存在单调映射关系。充分性越高,确定性也越高;必要性越高,简并性则越小。
因果度量指标的因果元语表示
| 因果指标 | 概率定义 | 因果元语定义 | 参考文献 |
|---|---|---|---|
| 有效信息EI | [math]\displaystyle{ \log_2{\frac{P(e|c)}{P(e|C)}} }[/math] | [math]\displaystyle{ \log_2\frac{suff}{1 - nec'} }[/math] | [2] |
| Galton度量 | [math]\displaystyle{ P(c)P(C\backslash c)(P(e|c) - P(e|C\backslash c)) }[/math] | [math]\displaystyle{ P(c)P(C\backslash c)(suff + nec - 1) }[/math] | [13] |
| Suppes度量 | [math]\displaystyle{ P(e|c) - P(e|C) }[/math] | [math]\displaystyle{ suff + nec' - 1 }[/math] | [14] |
| Eells度量(等同于Judea Pearl的充要概率PNS) | [math]\displaystyle{ P(e|c) - P(e|C\backslash c) }[/math] | [math]\displaystyle{ suff + nec - 1 }[/math] | [3][15] |
| Cheng度量(等同于Judea Pearl的充分概率PS) | [math]\displaystyle{ \frac{P(e|c) - P(e|C\backslash c)}{1 - P(e|C\backslash c)} }[/math] | [math]\displaystyle{ \frac{suff + nec - 1}{nec} }[/math] | [3][16] |
| Lewis度量(等同于Judea Pearl的必要概率PN) | [math]\displaystyle{ \frac{P(e|c) - P(e|C\backslash c)}{P(e|c)} }[/math] | [math]\displaystyle{ \frac{suff + nec - 1}{suff} }[/math] | [3][17] |
EI与动力学可逆性
正如示例example中的马尔科夫链所示,当概率转移矩阵呈现为一种排列置换矩阵(Permutation matrix)的时候,EI会更大。
可以证明,排列置换矩阵是唯一一种能同时满足如下两个条件的矩阵:
1、矩阵是可逆的; 2、矩阵满足马尔科夫链的归一化条件,也就是对于任意的[math]i\in[1,N][/math]来说,[math]|P_i|_1=1[/math]
我们将这一性质称为动力学可逆性[9]。因此,从某种程度上说,EI衡量的是马尔科夫链的一种动力学可逆性。
需要注意的是,这里所说的马尔科夫链的动力学可逆性与通常意义下的马尔科夫链的可逆性是不等同的。前者的可逆性体现为马尔科夫概率转移矩阵的可逆性,也就是它针对状态空间中的每一个确定性状态的运算都是可逆的,所以也称其为动力学可逆的。但是,文献中通常意义下的可逆的马尔科夫链并不要求转移矩阵是可逆的,而是要以稳态分布为时间反演对称轴,使得在动力学P作用构成的演化下的正向时间形成的状态分布序列和逆向状态分布序列完全相同。
由于排列置换矩阵过于特殊,我们需要能够衡量一般的马尔科夫概率转移矩阵与排列置换矩阵的靠近程度,以度量其近似动力学可逆性。在文献[9]中,作者们提出了一种用矩阵的类Schatten范数来度量一个马尔科夫概率转移矩阵的近似动力学可逆性的方法,定义为:
[math]\displaystyle{ \Gamma_{\alpha}\equiv \sum_{i=1}^N\sigma_i^{\alpha}=|P|_{\alpha}^{\alpha} }[/math]
这里,[math]|P|_{\alpha}[/math]为矩阵P的Schatten范数,[math]\Gamma_{\alpha}[/math]为近似动力学可逆性指标,[math]\sigma_i[/math]为概率转移矩阵P的奇异值,并且按照从大到小的顺序排列,[math]\alpha\in(0,2)[/math]为一个指定的参数,它起到让[math]\Gamma_{\alpha}[/math]能够更多地反映确定性还是简并性这样一种权重或倾向性。事实上,不难看出,如果让[math]\alpha\rightarrow 0[/math],则[math]\Gamma_{\alpha}[/math]就退化成了矩阵P的秩,即:
[math]\displaystyle{ rank(P)=\sum_{i=1}^N\sigma_i^{0} }[/math]
而矩阵的秩衡量的是矩阵P非退化(也就是可逆)的程度,与Degeneracy有着类似的效果。
而当[math]\alpha\rightarrow 2[/math],则[math]\Gamma_{\alpha}[/math]就退化成了矩阵P的Frobinius范数的平方,即:
[math]\displaystyle{ ||P||_F^2=\sum_{i=1}^N\sigma_i^{2} }[/math]
这一指标衡量的是矩阵P的确定性的程度,这是因为只有当矩阵P中的所有行向量都是独热向量(one-hot)的时候,[math]||P||_F[/math]才会最大,因此它与Determinism有着类似的衡量效果。
所以,当[math]\alpha\in(0,2)[/math]连续变化的时候,[math]\Gamma_{\alpha}[/math]就可以在简并性与确定性二者之间切换了。通常情况下,我们取[math]\alpha=1[/math],这可以让[math]\Gamma_{\alpha}[/math]能够在确定性与简并性之间达到一种平衡。
在文献[9]中,作者们证明了EI与动力学可逆性[math]\Gamma_{\alpha}[/math]之间存在着一种近似的关系:
[math]\displaystyle{ EI\sim \log\Gamma_{\alpha} }[/math]
关于马尔科夫链的近似动力学可逆性的进一步讨论和说明,请参考词条:近似动力学可逆性,以及论文:[9]
EI与JS散度
根据2的表达式,我们知道,EI实际上是一种广义的JS散度,即Jensen-Shannon divergence。
所谓的JS散度是一种度量两个定义在同一个支撑集上的概率分布之间差异的指标。设两个定义在支撑集[math]\mathcal{X}[/math]上的概率分布[math]P[/math]和[math]Q[/math],它们之间的JS散度定义为:
[math]\displaystyle{ JSD(P||Q)\equiv \frac{1}{2}D_{KL}(P||M)+\frac{1}{2}D_{KL}(Q||M) }[/math]
其中,[math]M=\frac{P+Q}{2}=\frac{1}{2}\sum_{x\in\mathcal{X}}\left[P(x)+Q(x)\right][/math]为P和Q的平均分布,[math]D_{KL}[/math]为KL散度。
与KL散度相比,JS散度是一种对称的度量,即[math]JSD(P||Q)=JSD(Q||P)[/math],而KL散度是非对称的。
可以看出,该式与2式的相似之处。不难验证,当P和Q都是2维向量,且构成了一个马尔科夫转移矩阵K的时候,K的EI就是P、Q的JS散度。
-
[math]\displaystyle{ JSD_{\pi}(P_1,P_2,\cdots,P_n)\equiv H(\sum_{i=1}^n\pi_iP_i)-\sum_{i=1}^n\pi_i H(P_i) }[/math]
(GJSD)
其中,[math]P_i,i\in[1,m][/math]为一组概率分布向量,m为它们的维度,而[math]\pi=(\pi_1,\pi_2,\cdots,\pi_n)[/math]为一组权重,并满足:[math]\pi_i\in[0,1],\forall i\in[1,n][/math]和[math]\sum_{i=1}^n\pi_i=1[/math]。
通过与公式tow_terms比较,不难发现,当[math]\pi_i=\frac{1}{n}[/math],则[math]JSD_{\pi}[/math]就退化为EI了。
在文献[19]中,作者们讨论了广义JS散度在分类多样性度量方面的应用。因此,EI也可以理解为是对行向量多样化程度的一种度量。
进一步,如果我们将Shannon熵[math]H(P_i)[/math]看做一个函数,则不难验证,H是一个凹函数,那么公式GJSD实际上是H函数的Jensen差距,即Jensen Gap。关于这一差距的数学性质,包括它的上下界估计,有大量的论文进行讨论[20]。
参考文献
- ↑ 1.0 1.1 Tononi, G.; Sporns, O. (2003). "Measuring information integration". BMC Neuroscience. 4 (31).
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 Hoel, Erik P.; Albantakis, L.; Tononi, G. (2013). "Quantifying causal emergence shows that macro can beat micro". Proceedings of the National Academy of Sciences. 110 (49): 19790–19795.
- ↑ 3.0 3.1 3.2 3.3 3.4 Judea Pearl; 刘礼; 杨矫云; 廖军; 李廉 (4 2022). 因果论——模型、推理和推断. 机械工业出版社.
- ↑ 4.0 4.1 Chvykov P; Hoel E. (2021). "Causal Geometry". Entropy. 23 (1): 24.
- ↑ 5.0 5.1 5.2 5.3 5.4 Zhang, Jiang; Liu, Kaiwei (2022). "Neural Information Squeezer for Causal Emergence". Entropy. 25 (1): 26.
- ↑ 6.0 6.1 Mingzhe Yang; Zhipeng Wang; Kaiwei Liu; Yingqi Rong; Bing Yuan; Jiang Zhang (2024). "Finding emergence in data by maximizing effective information". arXiv: 2308.09952.
- ↑ 7.0 7.1 7.2 Kaiwei Liu; Bing Yuan; Jiang Zhang (2024). "An Exact Theory of Causal Emergence for Stochastic Iterative Systems". arXiv: 2405.09207.
- ↑ Yuan, Bing; Zhang, Jiang; Lyu, Aobo; Wu, Jiaying; Wang, Zhipeng; Yang, Mingzhe; Liu, Kaiwei; Mou, Muyun; Cui, Peng (2024). "Emergence and Causality in Complex Systems: A Survey of Causal Emergence and Related Quantitative Studies". Entropy. 26 (2): 108.
- ↑ 9.0 9.1 9.2 9.3 9.4 Jiang Zhang; Ruyi Tao; Keng Hou Leong; Mingzhe Yang; Bing Yuan (2024). "Dynamical reversibility and a new theory of causal emergence". arXiv.
- ↑ Hoel, E.P. (2017). "When the Map Is Better Than the Territory". Entropy. 19: 188.
- ↑ 11.0 11.1 GIULIO TONONI (2008). "Consciousness as Integrated Information: a Provisional Manifesto". Biol. Bull. 215: 216–242.
- ↑ 12.0 12.1 Comolatti, R., & Hoel, E. (2022). Causal emergence is widespread across measures of causation. arXiv preprint arXiv:2202.01854.
- ↑ Fitelson, B., & Hitchcock, C. (2011). Probabilistic measures of causal strength (pp. 600-627). na.
- ↑ Suppes, P. (1973). A probabilistic theory of causality. British Journal for the Philosophy of Science, 24(4).
- ↑ Eells, E. (1991). Probabilistic causality (Vol. 1). Cambridge University Press.
- ↑ Cheng, P. W., & Novick, L. R. (1991). Causes versus enabling conditions. Cognition, 40(1-2), 83-120.
- ↑ Lewis, D. (1973). Causation. The journal of philosophy, 70(17), 556-567.
- ↑ Jianhua Lin (1991). "Divergence Measures Based on the Shannon Entropy". IEEE TRANSACTIONS ON INFORMATION THEORY. 37 (1): 145-151.
- ↑ Erik Englesson; Hossein Azizpour (2021). Generalized Jensen-Shannon Divergence Loss for Learning with Noisy Labels. 35th Conference on Neural Information Processing Systems (NeurIPS 2021).
- ↑ Gao, Xiang; Sitharam, Meera; Roitberg, Adrian (2019). "Bounds on the Jensen Gap, and Implications for Mean-Concentrated Distributions" (PDF). The Australian Journal of Mathematical Analysis and Applications. 16 (2). arXiv:1712.05267.
编者推荐
下面是一些链接能够帮助读者更好的了解因果涌现的相关信息:
因果涌现读书会
文章推荐
- Zhang, J.; Liu, K. Neural Information Squeezer for Causal Emergence. Entropy 2023, 25, 26.
- Yuan, B.; Zhang, J. et al. Emergence and Causality in Complex Systems: A Survey of Causal Emergence and Related Quantitative Studies. Entropy 2024, 26, 108.
路径推荐
- 张江老师根据因果涌现读书会第一季梳理的关于因果涌现的学习路径:https://pattern.swarma.org/article/153
- 张江老师根据因果涌现前五季读书会整理的因果涌现入门路径:https://pattern.swarma.org/article/296
此词条由张江编写,张江、袁冰、刘凯威、杨明哲和王志鹏整理和审校。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。