神经网络的有效信息计算
人工神经网络(artificial neural networks)主要通过分析节点与数据集间的互信息(Mutual Information,MI),来研究其对输入的响应。然而,神经网络还可以在因果关系层面进行探讨,揭示网络内部各层间“谁影响谁”及其作用机制。有效信息(Effective Information, EI)作为一种基于信息论的工具,可以通过最大熵扰动下的输入与输出之间的互信息,量化网络层间的因果作用。通过引入EI方法,我们能够在因果平面(Causal Plane)中观察网络训练过程中各层因果结构的演化,从而揭示不同任务对网络结构的需求,提供提升人工神经网络泛化能力和可解释性的新思路。
简介
人工神经网络在语音合成[1]、图像识别[2][3]和翻译[4]等各个领域都表现出了先进的性能。然而,人工神经网络底层机制还存在很多未知。例如,基本的机器学习理论表明,拥有大量参数的模型往往容易记住数据集中的所有信息,导致泛化能力差,特别是在未正则化的模型中[5]。深度神经网络(DNN)的主要原理是将深度学习技术[6]引入人工神经网络,以及将GPU用于高速计算[7]。在实践中,研究者发现即使没有显式正则化的DNN也具有良好的泛化性能[8]。虽然众所周知,尽管人工神经网络可以逼近任何函数[9],但它们得出的函数是如何超越训练数据进行泛化的,仍缺乏清晰的理论解释。
信息瓶颈(information bottleneck)是一种被提出来解释人工神经网络泛化能力的理论框架[10]。它认为神经网络在压缩输入数据与预测输出之间寻找最佳平衡。通过分析网络在信息平面(information plane)上的行为——即输入数据与每层网络之间的互信息,研究者尝试揭示网络的学习机制[11]。虽然寻找信息瓶颈是一个可行的方法,但更大的网络仍然受到信息估计问题的困扰[12],并且某些网络拓扑和激活函数的预测或偏差存在错误[13]。更根本的是,信息瓶颈方法的数学公式是数据依赖的,也就是说,它的互信息得分随着输入分布的变化而变化。然而,从定义上讲,泛化能力是不同数据集(输入频率不同,甚至是未知且尚未定义的未来数据集)性能的函数。因此,为了理解泛化能力,有必要关注神经网络在具有不同属性的不同数据集上的不变性[14]。
为更深入理解神经网络的泛化能力,我们需要关注网络中独立于数据分布的因果结构。因果结构描述了网络中节点间的依赖关系,反映了节点之间的连接机制和作用方式。这里我们介绍一种微扰方法,该方法使用信息理论以逐层的方式跟踪神经网络内的因果作用。具体来说,我们引入了有效信息(Effective Information, EI),它可以捕获因果关系的信息量和强度。EI最初是作为复杂系统两个子集之间因果关系的信息论度量而引入的[15]。已经有学者证明,EI可以量化布尔网络的因果结构[16],也可以量化图形[17]。值得注意的是,EI与信息瓶颈方法在数学上有相似之处,但EI侧重于因果关系。在神经网络中,EI通过对网络层节点施加独立且随机的最大熵噪声,计算扰动后输出与输入之间的互信息,捕捉层间因果结构的信息总量。研究发现,网络训练过程中损失函数的快速下降往往伴随着EI的剧烈变化,揭示了网络因果结构的动态演化。
更重要的是,EI可以帮助我们追踪网络训练过程中各层因果结构的变化路径,称之为因果平面(causal plane)。通过观察网络连接的“敏感度”(Sensitivity,即扰动的传递效果,类似Erik Hoel的Determinism概念[18])和“简并度”(Degeneracy,即连接重叠导致的信息丢失),我们可以看到不同任务如何塑造神经网络的因果结构。复杂任务往往导致网络因果结构分化更明显,而简单任务中这种分化较弱。此外,冗余层通常无法在因果平面中显著变化,显示其对网络功能贡献较小。此外,我们会展示如何使用EI来计算一层中节点的总联合效应和总个体效应之间的差异,从而可以测量神经网络中的前馈集成信息[19]。
这种分析工具为解决人工神经网络的可解释性问题提供了新的思路。由于人工神经网络拥有大量参数,常被视为“黑匣子”,其内部机制难以理解,影响了模型的透明度[20]。缺乏可解释性可能会掩盖其他问题,如数据集[21]或模型选择[22]中的偏见,对于那些想使用人工神经网络做出关于人生命的事情来说是一个重大问题,例如在自动驾驶汽车[23]、自动驾驶无人机[24]或医疗诊断[25]的情况下。因此使用这套技术,研究人员将能够在训练过程中直接观察神经网络的整体因果结构发生变化的过程,这是打开“黑匣子”和了解神经网络中的作用的关键一步。
有效信息量化神经网络因果结构
干预揭示因果关系
干预(也称为“扰动”)是揭示因果关系的关键工具。前馈深度神经网络(DNN)的因果关系集合(也称为“因果结构”)由多个层、层之间的连接以及节点的激活函数组成。我们引入了一套工具,用于探索一个假设:DNN的泛化能力取决于其因果结构如何适应所训练的任务(详见 https://github.com/ei-research-group/deep-ei )。
为了研究这一问题,我们采用了一种广泛用于因果分析的正式方法,其中干预被表示为对系统中的某个变量应用[math]\displaystyle{ do(x) }[/math]操作符[26]。通常,[math]\displaystyle{ do(x) }[/math]用于将一个变量设置为特定值,例如在有向无环图中,它可以用来对单个节点进行干预(例如,之前在DNN中已用于应用单个干预[27]。[math]\displaystyle{ do(x) }[/math]通常用于将给定系统中的单个变量(如有向无环图)设置为特定值(例如,它以前曾被用于在DNN中应用单个干预[28][29])。然而,我们在这里引入了一种新的方法,即使用“干预分布”(Intervention Distribution, [math]\displaystyle{ I_D }[/math]),它是对[math]\displaystyle{ do(x) }[/math]操作符的概率分布描述。简单来说,[math]\displaystyle{ I_D }[/math]是对一系列干预的数学描述。当我们在一个网络层的输入上应用[math]\displaystyle{ I_D }[/math]时,会导致输出节点产生某种效应分布([math]\displaystyle{ E_D }[/math])[30]。
通过信息理论,我们可以量化这些因果关系的信息量。更强的因果关系意味着它们传递了更多的信息。我们使用有效信息(Effective Information, EI)来衡量因果关系的强度。具体来说,EI是干预分布([math]\displaystyle{ I_D }[/math])和效应分布([math]\displaystyle{ E_D }[/math])之间的互信息(Mutual Information, MI),当[math]\displaystyle{ I_D }[/math]为最大熵分布(即[math]\displaystyle{ H^{max} }[/math])时。换句话说,EI是通过向网络注入噪声(随机化)后计算的互信息。这种随机化有多个作用:首先,它确保了所有传递的互信息都是由噪声引起的,而不是简单的相关性;其次,作为最大熵的干预,EI反映了随机化变量所产生的信息量,这在科学中是因果关系的“黄金标准”;最后,EI可以被视为对输入状态空间的无偏采样,反映了网络如何处理分布外的数据。
此外,EI还可以被理解为衡量函数映射的“图像”如何帮助恢复“原像”,并且与Kolmogorov复杂度和VC熵有重要关系[31]。最重要的是,先前的研究表明,EI能够反映因果关系的重要特性,例如其确定性(缺乏噪声)或退化性(缺乏唯一性)[16],而这些特性是标准互信息无法捕捉的。
测量层与层之间的有效信息
首先我们介绍一种方法,用于测量深度神经网络中层与层之间的有效信息,从而捕捉一个层对另一个层的总联合效应。因此,我们从L1开始,L1是一组与L2有加权前馈连接的节点,我们假设所有节点都有一些激活函数,如sigmoid函数。为了测量EI,L1在最大熵[math]\displaystyle{ do(L_{1}=H^{\max}) }[/math]处受到扰动,这意味着节点的所有激活都被迫进入随机选择的状态。[math]\displaystyle{ L_{1}=H^{\max} }[/math]最大限度地放大了L1中所有节点的同时和独立的最大熵扰动:
[math]\displaystyle{ \begin{equation} EI = I(L_1, L_2) \mid do(L_1 = H^{\text{max}}) \end{equation} }[/math]
这个公式表示在L1被最大熵扰动的情况下,L1和L2之间的互信息。
有效信息在不同激活函数中的表现
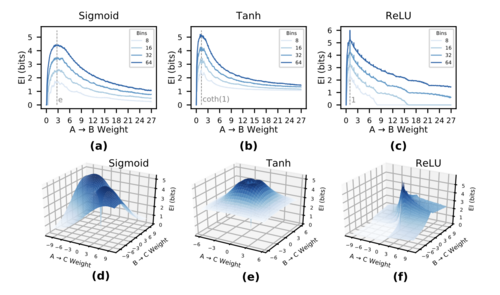
EI在不同的常用激活函数中具有一致的特性。下图a-c展示了两个节点A和B之间单个连接的EI,其中A→B的权重逐渐增加,每个面板展示了不同的激活函数(sigmoid、tanh、ReLU)。我们可以看到,对于每个具有特定激活函数的孤立连接,存在一个依赖于A到B连接权重的特征EI曲线,并且该曲线的形状与选择的bins数量(8、16、32和64)无关。
在低权重时,EI表明B对A的扰动不敏感,尽管这种敏感性在所有三个激活函数中都会上升到一个峰值。随着权重的增加,激活函数趋于饱和,B对A的扰动变得不敏感,EI曲线随之下降。
值得注意的是,这些特征峰值揭示了哪些权重代表了强因果关系(在孤立连接的情况下)。例如,sigmoid激活函数在权重等于欧拉数e时具有最具信息量的因果关系,tanh激活函数在权重为coth(1)时达到峰值,而ReLU激活函数在权重为1时达到峰值。这表明,DNN中最重要的权重可能是最具因果效力的,而不是绝对值最高的权重。例如,在使用sigmoid激活函数时,如果A→B的连接权重非常高,A的激活对扰动的信息量会变得很小,因为大多数扰动都会导致B的输出饱和到1。
多连接情况下的EI曲线
在存在多个连接的情况下,EI曲线会变成一个更高维的EI流形。下图d-f展示了由两个节点A和B组成的层,每个节点都有一个连接到C的单个连接的EI (A, B→C)。由于扰动之间可能相互干扰,EI不仅取决于节点之间关系的敏感性,还取决于网络连接的重叠或简并性,从而形成一个流形。例如,在sigmoid激活函数中,EI流形大致是2倍对称的,这是由于sigmoid函数在正负权重周围的对称性,以及网络本身的对称性(因为神经元A和B都只连接到C)。
复杂度对因果结构的影响
为了研究深度神经网络(DNN)在学习过程中因果结构的变化,我们使用了两个经典的分类任务来训练网络:Iris[32]和MNIST[33]。通过跟踪有效信息变化,我们能够揭示网络内部因果结构的演化,并进一步说明复杂度对因果结构的影响。
训练过程我们使用以下架构。(1)Iris任务:我们使用了一个四层神经网络,结构为4→5→5→3。输入层有4个神经元,对应Iris数据集的4个特征(如花萼长度、花萼宽度等);两个隐藏层各有5个神经元;输出层有3个神经元,对应3种鸢尾花的分类。(2)MNIST任务:我们使用了一个四层神经网络,结构为25→6→6→5。输入层有25个神经元,对应5x5的输入图像(原始MNIST图像为28x28,我们进行了降维处理);两个隐藏层各有6个神经元;输出层有5个神经元,对应数字0到4的分类(我们删除了数字5到9以简化任务)。
在训练参数上的选取上如下。我们使用均方误差(MSE)作为损失函数,梯度下降作为优化算法,学习率为0.01。Iris网络训练了4000个epoch,批量大小为10;MNIST网络训练了500个epoch,批量大小为50。权重初始化采用均匀分布,确保初始权重在合理范围内。权重从以下分布中采样: [math]\displaystyle{ W_{ij} = \mathscr{U}\left([ -\frac{1}{\sqrt{\mathrm{fan}_{\mathrm{in}}}}, \frac{1}{\sqrt{\mathrm{fan}_{\mathrm{in}}}} ]\right) }[/math]。为了计算EI,我们使用了固定长度的噪声注入(10^7个样本),以确保结果的收敛性。
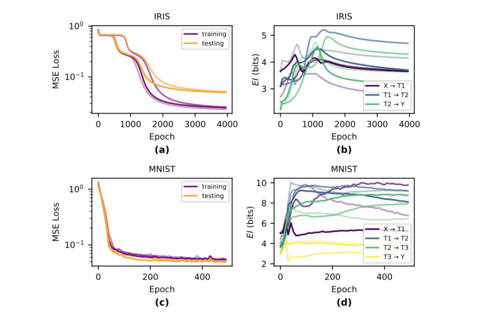
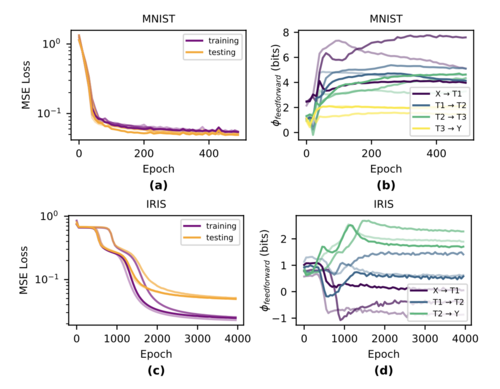
训练结果如下图所示。(a)和(c)分别展示了在Iris和MNIST任务中,均方误差损失(MSE Loss)随训练epoch的变化情况。在训练初期,两个任务的训练损失和测试损失都迅速下降,表明模型正在快速学习任务;随着epoch的增加,损失逐渐趋于平稳,表明模型的学习速度减慢。在后期,训练损失继续下降,但测试损失趋于稳定甚至略有上升,表明模型可能开始过拟合。Iris 任务由于相对简单,损失下降较快且过拟合现象不明显;而MNIST任务更复杂,损失下降较慢且过拟合现象更为明显。下图(b)和(d)展示了Iris和MNIST任务中EI随训练epoch的变化情况。Iris任务:图中显示了输入层到第一个隐藏层(X→T1)、第一个隐藏层到第二个隐藏层(T1→T2)、以及第二个隐藏层到输出层(T2→Y)的EI变化。可以看到,EI在训练初期变化显著,随着网络逐渐拟合任务,EI趋于稳定。MNIST任务:图中显示了第一个隐藏层到第二个隐藏层(T1→T2)、第二个隐藏层到第三个隐藏层(T2→T3)、以及第三个隐藏层到输出层(T3→Y)的EI变化。与Iris任务相比,MNIST任务的EI变化更加显著,表明复杂任务导致网络层的因果结构分化更大。以上结果说明任务复杂度对因果结构的影响:对于更复杂的任务(如MNIST),网络层的因果结构在训练过程中表现出更大的分化,不同层的EI变化更加显著。而对于较简单的任务(如Iris),因果结构的分化较少,EI的变化也相对较小。
神经网络中的因果平面
有效信息分解
如上文所述,有效信息取决于网络中连接的权重以及这些权重之间的重叠程度。这两者共同构成了EI流形。这意味着EI可以分解为两个关键属性:敏感度(Sensitivity)和简并度(Degeneracy)。敏感度衡量网络中每条边独立传输信息的能力,而简并度衡量由于边权重重叠导致的信息损失。这种分解方式类似于之前在布尔网络或马尔可夫链中将EI分解为确定性和简并度的做法[16][17]。不过,在神经网络中,由于网络是确定性的,我们用敏感度代替了确定性。
在深度神经网络(DNN)中,敏感度衡量输入层的扰动能够多大程度地传递到输出层。如果敏感度高,说明网络对输入的变化非常敏感。而简并度衡量通过输出层的激活值能否重建输入层的扰动源。如果简并度高,说明网络中的信息重叠较多,导致扰动源难以被准确重建。这两个属性共同构成了一个称为因果平面的二维空间,所有神经网络层都可以在这个平面中找到自己的位置。随着网络的学习,不同层的因果结构会逐渐分化,反映出它们对网络功能的贡献。
为了量化这些属性,敏感度是通过计算网络中每条边的独立贡献来衡量的。具体公式为:
[math]\displaystyle{ \text{Sensitivity} = \sum_{\substack{i \in L_1 \\ j \in L_2}} I(t_i, t_j) \mid \operatorname{do}(i = H^{\text{max}}) }[/math]
其中,[math]\displaystyle{ L_1 }[/math] 和 [math]\displaystyle{ L_2 }[/math] 分别是输入层和输出层,[math]\displaystyle{ I(t_i, t_j) }[/math] 是输入节点 [math]\displaystyle{ i }[/math] 和输出节点 [math]\displaystyle{ j }[/math] 之间的互信息,[math]\displaystyle{ \operatorname{do}(i = H^{\text{max}}) }[/math] 表示对输入节点 [math]\displaystyle{ i }[/math] 进行最大熵扰动。如果网络中的每个节点只接收一个唯一的输入(即没有重叠),那么敏感度就等于EI。
简并度衡量的是由于边权重重叠导致的信息损失,计算公式为:
[math]\displaystyle{ \text{Degeneracy} = \text{Sensitivity} - EI }[/math]
简并度越高,说明网络中的信息重叠越多,导致信息传递的效率降低。
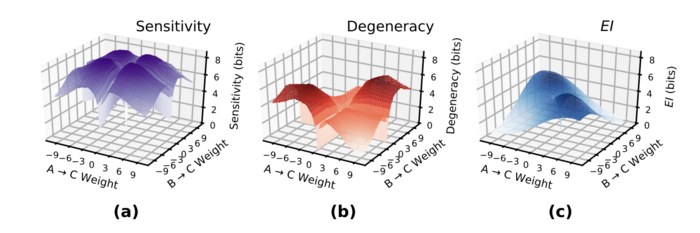
下图展示了有效信息(EI)如何由敏感度(Sensitivity)和简并度(Degeneracy)组成。图中显示了具有两个输入节点和一个输出节点的网络层(使用S形激活函数)的敏感度和简并度曲面。(a)展示了敏感度的曲面,表示网络中每条边独立传输信息的能力。(b)展示了简并度的曲面,表示由于边权重重叠导致的信息损失。(c)展示了EI 流形,它是通过将图(b)的简并度曲面从图(a)的敏感度曲面中减去得到的。因此我们可以直观地看到敏感度和简并度如何共同决定了有效信息的分布。
因果平面
为了可视化网络层在训练过程中的变化,我们引入了因果平面。因果平面的两个维度分别是敏感度和简并度。由于 [math]\displaystyle{ EI = \text{Sensitivity} - \text{Degeneracy} }[/math],如果敏感度和简并度同时增加,EI将保持不变。在因果平面中,[math]\displaystyle{ y = x }[/math] 的直线称为EI的零线,表示 [math]\displaystyle{ EI = 0 }[/math]。向敏感度方向移动表示网络对扰动的敏感性增加,EI增加;向简并度方向移动表示网络的简并度增加,EI减少;沿零线移动表示EI保持不变,网络层的因果结构没有显著变化。
网络层因果结构分化
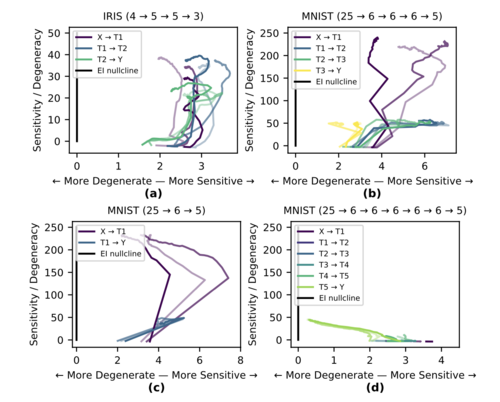
下图展示了我们在实验中观察到的现象。MNIST由于任务更复杂,网络层的因果结构在因果平面中表现出更大的分化(图b-d)。而Iris由于任务较简单,网络层的因果结构分化较少,且更倾向于沿EI零线移动(图a)。此外,我们还发现,冗余层在因果平面中移动较少,表明它们对网络因果结构的贡献有限,而动态层在因果平面中表现出更大的移动,反映出它们对网络功能的重要贡献(图d)。
有效信息量化联合效应与独立效应
综合信息理论(IIT)已被用于评估系统中联合效应与独立效应所包含的总信息[34]。它是因果分析的有用工具,分析网络因果结构中整合的信息量[35][36]。以前,综合信息被衡量为给定分区的EI损失[37],使EI成为综合信息的上限。然而,目前还没有一种公认的通用综合信息衡量标准[38]。相反,在不同的系统中提出了各种集成信息的措施[39][40]。传统上,前馈网络中的集成信息量为零,因为没有可重入连接,因为它基于在系统的所有可能子集中找到最小信息分区。然而,即使在前馈网络中,一层的节点仍然可能对另一层产生不可约的联合效应,因此我们引入了一种度量,即前馈集成信息,应用于DNN。
通常,计算集成信息需要检查所有可能分区的集合,这使得这种方法不适用于维数较小的系统。或者,为了评估单个边对EI的协同贡献,可能需要使用多变量信息理论,例如部分信息分解,当包含源时,它会按照Dedekind数的顺序增长[41]
为了避免这些问题,我们引入了一种基于每条边的贡献计算的度量方法[math]\displaystyle{ EI_{parts} }[/math]。也就是说,对于每个节点i∈L1,记录其在该扰动下的激活函数的时间序列估计,以及每个节点j∈L2的激活函数。为了计算EI部分,然后将每个节点的每个单独的时间序列离散为一些共享的选定bin大小,并计算和求和每个(i,j)对的MI:10)。
[math]\displaystyle{ \begin{equation} EI_{\text{parts}}(L_1 \rightarrow L_2) = \sum_{(i \in L_1, j \in L_2)} I(t_i, t_j) \mid \text{do}(L_1 = H^{\max}). \end{equation} }[/math]
请注意,对于具有单个节点的层,EI和EI部分是相同的。当网络的每个节点只接收单个边缘时,情况也是如此。然而,[math]\displaystyle{ EI_{parts} }[/math]措施必然会错过某些积极的联合效应。重要的是,EI和EIparts度量之间的差异可以捕捉到联合效应的量,从而捕捉到逐层以前馈方式整合的信息量。具体来说,我们将EI(综合信息的上限)与第3节中定义的[math]\displaystyle{ EI_{parts} }[/math]进行比较,即[math]\displaystyle{ \Phi_{feedforward} = EI - EI_{parts} }[/math]。应该指出的是,向前的φf虽然旨在捕捉一层到另一层的总联合效应,但不受零的限制,可以是负的。
为了了解DNN训练过程中层间联合效应的变化,我们分析了Iris和MNIST数据集训练过程中[math]\displaystyle{ φ_f }[/math]的前向变化(有关我们测量[math]\displaystyle{ EI_{parts} }[/math]的方法的详细信息,请参阅SI第7.1节)。我们观察到,MNIST训练的网络比Iris训练的网络具有更高的φf前馈,这表明因果结构确实根据任务的复杂性而有所不同,需要更多的联合效应来学习(见下图)。
总结
在这里,我们引入了信息论技术,根据扰动后的信息流对DNN的因果结构进行分类和量化。这些技术是围绕有效信息(EI)构建的,我们将其应用于DNN。它被定义为在一组最大熵扰动之后的互信息,它揭示了层因果结构中包含的信息。对于在Iris和MNIST任务上训练的网络,EI在训练期间发生了变化,特别是在实际发生学习时(如损失函数中的阶跃变化所反映的)。
EI取决于网络的灵敏度和简并性。两个节点之间的灵敏度反映了孤立因果关系的强度,并在不同激活函数的特定特征权重处达到峰值(例如,在sigmoid激活函数中,它达到峰值)。层的退化反映了由于边缘权重的重叠,上游扰动的下游重建的困难。分析EI揭示了网络在灵敏度/简并空间上的位置,我们称之为“因果平面”。将网络架构放置在这个平面上的能力意味着我们可以跟踪任何给定的DNN的因果结构在训练过程中如何在空间中演变。我们的结果表明,DNN的因果结构反映了它所训练的任务。例如,在MNIST任务中,DNN因果结构中的不同层有一个明确的任务,这反映在每一层在因果平面上的不同轨迹上,添加新的冗余层不会对EI产生影响,因此不会向因果结构添加新的信息。
这些技术提供了一种与信息瓶颈研究不同的方法[42],后者侧重于使用互信息来衡量输入和节点活动之间的相关性。这两种方法都有类似的目标来解释DNN的泛化性,并且都有形式上的相似之处,尽管这里的重点是逐层因果结构本身,而不是DNN的输入。未来,这项工作可以扩展到这里考虑的三种激活函数之外的不同激活函数[43][44]、无监督任务[45]、LSTM等循环神经网络[46]和卷积神经网络[2]。
这些技术开辟了评估EI分解和扩展的可能性,例如DNN的集成信息(因为集成信息可以使用网络子集之间的最小EI来计算[15],集成信息也可以分解为类似于灵敏度和简并性的属性[47]。这里,概述了一种综合信息的度量方法φf forward,用于度量前馈层连通性中的不可约联合效应。 所有这些可能有助于理解为什么某些网络架构具有普遍性,为什么有些没有。未来,这些技术也为直接测量DNN中的个别因果关系提供了可能性[36]。
参考文献
- ↑ Zhizheng Wu, Oliver Watts, and Simon King. Merlin: An open source neural network speech synthesis system. In SSW, pages 202–207, 2016.
- ↑ 2.0 2.1 Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105, 2012.
- ↑ Edgar Xi, Selina Bing, and Yang Jin. Capsule network performance on complex data. arXiv preprint arXiv:1712.03480, 2017.
- ↑ I Sutskever, O Vinyals, and QV Le. Sequence to sequence learning with neural networks. Advances in NIPS, 2014.
- ↑ Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning requires rethinking generalization. arXiv preprint arXiv:1611.03530, 2016.
- ↑ Yann LeCun, Yoshua Bengio, and Geoffrey Hinton. Deep learning. nature, 521(7553):436–444, 2015.
- ↑ Rajat Raina, Anand Madhavan, and Andrew Y Ng. Large-scale deep unsupervised learning using graphics processors. In Proceedings of the 26th annual international conference on machine learning, pages 873–880. ACM, 2009.
- ↑ Behnam Neyshabur, Srinadh Bhojanapalli, David McAllester, and Nati Srebro. Exploring generalization in deep learning. In Advances in Neural Information Processing Systems, pages 5947–5956, 2017.
- ↑ Kurt Hornik, Maxwell Stinchcombe, and Halbert White. Multilayer feedforward networks are universal approximators. Neural networks, 2(5):359–366, 1989.
- ↑ Naftali Tishby, Fernando C Pereira, and William Bialek. The information bottleneck method. arXiv preprint physics/0004057, 2000.
- ↑ Ravid Shwartz-Ziv and Naftali Tishby. Opening the black box of deep neural networks via information. arXiv preprint arXiv:1703.00810, 2017.
- ↑ Kristoffer Wickstrøm, Sigurd Løkse, Michael Kampffmeyer, Shujian Yu, Jose Principe, and Robert Jenssen. Information plane analysis of deep neural networks via matrix-based renyi’s entropy and tensor kernels.arXiv preprint arXiv:1909.11396, 2019.
- ↑ Andrew M Saxe, Yamini Bansal, Joel Dapello, Madhu Advani, Artemy Kolchinsky, Brendan D Tracey, and David DCox. On the information bottleneck theory of deep learning. Journal of Statistical Mechanics: Theory and Experiment, 2019(12):124020, 2019.
- ↑ Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning requires rethinking generalization. arXiv preprint arXiv:1611.03530, 2016.
- ↑ 15.0 15.1 Giulio Tononi and Olaf Sporns. Measuring information integration. BMC neuroscience, 4(1):31, 2003.
- ↑ 16.0 16.1 16.2 Erik P Hoel, Larissa Albantakis, and Giulio Tononi. Quantifying causal emergence shows that macro can beat micro. Proceedings of the National Academy of Sciences, 110(49):19790–19795, 2013.
- ↑ 17.0 17.1 Erik P Hoel, Larissa Albantakis, and Giulio Tononi. Quantifying causal emergence shows that macro can beat micro. Proceedings of the National Academy of Sciences, 110(49):19790–19795, 2013.
- ↑ Hoel, Erik P.; Albantakis, L.; Tononi, G. (2013). "Quantifying causal emergence shows that macro can beat micro". Proceedings of the National Academy of Sciences. 110 (49): 19790–19795.
- ↑ Masafumi Oizumi, Larissa Albantakis, and Giulio Tononi. From the phenomenology to the mechanisms of consciousness: integrated information theory 3.0. PLoS Comput Biol, 10(5):e1003588, 2014.
- ↑ David Gunning. Explainable artificial intelligence (xai). Defense Advanced Research Projects Agency (DARPA), nd Web, 2, 2017.
- ↑ Mohsan Alvi, Andrew Zisserman, and Christoffer Nellåker. Turning a blind eye: Explicit removal of biases and variation from deep neural network embeddings. In Proceedings of the European Conference on Computer Vision(ECCV) , pages 0–0, 2018.
- ↑ Arnaud Mignan and Marco Broccardo. One neuron versus deep learning in aftershock prediction. Nature, 574(7776): E1–E3, 2019.
- ↑ Mariusz Bojarski, Davide Del Testa, Daniel Dworakowski, Bernhard Firner, Beat Flepp, Prasoon Goyal, Lawrence D Jackel, Mathew Monfort, Urs Muller, Jiakai Zhang, et al. End to end learning for self-driving cars. arXiv preprint arXiv:1604.07316, 2016.
- ↑ Dario Floreano and Robert J Wood. Science, technology and the future of small autonomous drones. Nature, 521(7553):460–466, 2015.
- ↑ Hoo-Chang Shin, Holger R Roth, Mingchen Gao, Le Lu, Ziyue Xu, Isabella Nogues, Jianhua Yao, Daniel Mollura, and Ronald M Summers. Deep convolutional neural networks for computer-aided detection: Cnn architectures, dataset characteristics and transfer learning. IEEE transactions on medical imaging, 35(5):1285–1298, 2016.
- ↑ Judea Pearl. Causality. New York: Cambridge, 2000. doi: 10.1017/CBO9780511803161.
- ↑ Judea Pearl. Causality. New York: Cambridge, 2000. doi: 10.1017/CBO9780511803161.
- ↑ Michael Harradon, Jeff Druce, and Brian Ruttenberg. Causal learning and explanation of deep neural networks via autoencoded activations. arXiv preprint arXiv:1802.00541, 2018.
- ↑ Tanmayee Narendra, Anush Sankaran, Deepak Vijaykeerthy, and Senthil Mani. Explaining deep learning models using causal inference. arXiv preprint arXiv:1811.04376, 2018.
- ↑ Erik P. Hoel. When the map is better than the territory. Entropy, 19(5):188, 2017. ISSN 1099-4300. doi: 10.3390/e19050188.
- ↑ R. A. Fisher. The Design of Experiments. The American Mathematical Monthly, 43(3):180, 1936. ISSN 00029890. doi: 10.2307/2300364.
- ↑ R. A. Fisher. The Design of Experiments. The American Mathematical Monthly, 43(3):180, 1936. ISSN 00029890. doi: 10.2307/2300364.
- ↑ Yann LeCun, Corinna Cortes, and CJ Burges. Mnist handwritten digit database. ATT Labs [Online]. Available: http://yann.lecun.com/exdb/mnist, 2, 2010.
- ↑ Giulio Tononi. Consciousness as integrated information: a provisional manifesto. The Biological Bulletin, 215(3): 216–242, 2008.
- ↑ William Marshall, Hyunju Kim, Sara I Walker, Giulio Tononi, and Larissa Albantakis. How causal analysis can reveal autonomy in models of biological systems. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 375(2109):20160358, 2017.
- ↑ 36.0 36.1 Larissa Albantakis, William Marshall, Erik Hoel, and Giulio Tononi. What caused what? a quantitative account of actual causation using dynamical causal networks. Entropy, , 21(5):459, 2019.
- ↑ David Balduzzi and Giulio Tononi. Integrated information in discrete dynamical systems: motivation and theoretical framework. PLoS Comput Biol, 4(6):e1000091, 2008.
- ↑ Masafumi Oizumi, Larissa Albantakis, and Giulio Tononi. From the phenomenology to the mechanisms of consciousness: integrated information theory 3.0. PLoS Comput Biol, 10(5):e1003588, 2014.
- ↑ Max Tegmark. Improved measures of integrated information. PLoS computational biology, 12(11):e1005123, 2016.
- ↑ Pedro AM Mediano, Anil K Seth, and Adam B Barrett. Measuring integrated information: Comparison of candidate measures in theory and simulation. Entropy, 21(1):17, 2019.
- ↑ Paul L Williams and Randall D Beer. Nonnegative decomposition of multivariate information. arXiv preprint arXiv:1004.2515, 2010.
- ↑ Naftali Tishby and Noga Zaslavsky. Deep learning and the information bottleneck principle. In 2015 IEEE Information Theory Workshop (ITW) , pages 1–5. IEEE, 2015.
- ↑ Bekir Karlik and A Vehbi Olgac. Performance analysis of various activation functions in generalized mlp architectures of neural networks. International Journal of Artificial Intelligence and Expert Systems, 1(4):111–122, 2011.
- ↑ Vinod Nair and Geoffrey E Hinton. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th international conference on machine learning (ICML-10) , pages 807–814, 2010.
- ↑ Laurenz Wiskott and Terrence J Sejnowski. Slow feature analysis: Unsupervised learning of invariances. Neural computation, 14(4):715–770, 2002.
- ↑ Sepp Hochreiter and Jürgen Schmidhuber. Long short-term memory. Neural computation, 9(8):1735–1780, 1997.
- ↑ Erik P Hoel, Larissa Albantakis, William Marshall, and Giulio Tononi. Can the macro beat the micro? Integrated information across spatiotemporal scales. Neuroscience of Consciousness, 2016(1), 2016.