系统中的观察者(5)——自指
- 作者:jake
- 时间:2010-02
自指——连接图形与衬底的金带
在第二章《基本框架》中,我们曾对生命的本质进行过简单的探讨。按照第二章的说法,“那些可以被形式因和目的因解释的系统就具备智能和生命”。然而,这个答案仍然有些简单粗暴。观察者为什么凭白无故地将因果箭头转向?
在上一章《人工智能中的背景——玩家观察者》中,我们指出构建图灵机-观察者模型的一个重要目标就是要让计算机程序能够利用玩家的交互资源而不断地构建越来越深的虚拟层次。然而,计算机程序是如何构建虚拟层的?
所有这些问题都集中到一个古老而意义深远的名词:自指(Self-reference)。
本章的叙述框架如下:首先,在第1节中我们将简单回顾自指问题在数理逻辑、计算科学中的研究历史;其次,在第2节,我们专门论述了自然语言中的自指现象。这一节对整个章节的理解都至关重要,因为本节利用人们熟悉、容易理解的自然语言将后续部分自指中的所有关键概念、方法都概括了。所以,我希望读者能够花大力气搞懂这一小节,尤其是要透彻理解用蒯恩技术实现的间接自指,它是整个章节的精髓;然后,第3节主要介绍“自打印程序”,并试图用该程序说清建构性自指的概念;随后的第4节则将建构性自指升级,我们开始讨论递归定理,它被我称为“未开采的科学金矿”;第5节利用图灵停机问题和歌德尔定理(可跳过)作为实例介绍破坏性自指,我们将着重介绍蒯恩技术和自指悖论的构建方法;第6节将从另一个角度:“黄金对角线”,把第3、4、5节的主题重新论述一遍(此节可跳过),你会看到原来自指还可以有“几何表示法”;可以说前6节全部是在介绍有关自指的具体技术,只有到第7章才开始论述观察者与自指的关系。上一章提出的图灵机-观察者模型将会在这里重新发挥作用;第8节则进一步将观察者与自指的关系提升到因果逆转的高度,并从深层次指出生命的本质就在于这种因果逆转;最后,第9节对全章进行小结。
自指——一条永恒的金带
自指是一个非常古老的话题,它通常与古代奥义以及各种神秘哲学有关。例如佛教中所提倡的“观身无常、观心无我”,以及古希腊的“认识你自己”,都在劝解人们能够将心智的观察箭头指向自己。中国道家所倡导的“无”,正是一个最简单的一字悖论。
一幅最能体现自指深邃含义的图画莫过于这条正在吞噬自己的蛇。此蛇作为一种图腾曾广泛出现在北欧神话、基督教神学、印度教和非洲宗教之中。这条蛇将自指那种深刻的自我毁灭性体现得淋漓尽致——我们可以想象一下当它把自己吞噬完毕会产生怎样怪异的情景。
将这种自我毁灭性的古代奥义应用到现代科学中已经产生了一系列深刻的结论。首先,在19世纪末,著名数学家康托尔(George Cantor)将“对角线删除”法则应用到集合论中,从而证明了实数的个数比自然数多。紧接着,罗素(Bertrand Russell)提出了著名的“罗素悖论”而摧毁了弗雷格(Gottlob Frege)的数学大厦。年仅25岁的哥德尔(Kurt Gödel)巧妙地应用同样的破坏性自指一举摧毁了数学大师希尔伯特(David Hilbert)的完备一致性的数学体系梦想。图灵(Alan Turing)则利用同样的技巧进一步发现任何超级计算机都不可能求解的图灵停机问题。
纽约时报曾将哥德尔不完备定理评价为20世纪最伟大的数学定理。自指可以用来构造破坏性的悖论已经是众人皆知、司空见惯了。然而,这种认识其实很片面。自指包含了比自指悖论更宽泛的内容,因为在自指大家庭中,还包括另外一类构建性的成员。
1953年,正当人们举杯欢庆沃森和克里克发现了DNA双螺旋结构,并从分子层面上解释了生命的自我复制之谜的时候,另外一名伟大的美国匈牙利裔数学家:约翰.冯诺依曼(John von Neumann)正在独立地思考着生命自我复制的逻辑基础。然而,令人遗憾的是,那时的冯诺依曼已经患上了癌症,并于1957年的2月去世。于是,他的助手阿瑟.伯克斯Arthur Burks将他关于自复制自动机理论的整理成书《Theory of Self-reproducing Automata》,并于1966年出版。
与沃森.克里克不同的是,冯诺依曼要寻找的是生命自我复制的逻辑基础而非物质基础。虽然冯诺依曼没有明确指出,但是已经暗含了这个自复制的逻辑基础不是别的,正是一种自指结构。也就是说,自指恰恰是生命实现自我复制的逻辑内核。这也许会让读者感到困惑。不是说,自指都是用来构造诸如哥德尔定理、罗素悖论之类的破坏性武器吗?实际上,还存在着另外一大类自指,笔者称之为“建构性的自指”,它不但不会引起破坏,反而能够创造很多令人意想不到的惊奇结构。至于自我繁殖的系统是如何令人意想不到的,请参考第4节的讨论。
实际上,早在1938年,与哥德尔共同奠定递归函数论基础的数学家克林尼(Stephen Kleene)就证明了递归函数论中的一个著名定理:递归定理(更精确地说,应该叫Kleene第二递归定理)。根据它,人们可以很轻松地得到一个数学推论,系统的自我复制是可能的。
证明递归定理的核心技巧,是一个被称为“蒯(kuai3)恩”的特别技术。蒯恩(Willard.V. Quine)是美国的哲学家,终身致力于哲学、数理逻辑、集合论的研究。他创造了一种称之为蒯恩的方法,使得人们可以不通过使用“我”或者“这句话”等词语就能创造出可以谈论自身的句子来。
有趣的是,蒯恩构造恰恰就是那条“黄金对角线”(这一方法正是当年康托尔最早提出证明实数比自然数多的方法,也是哥德尔定理构造哥德尔句子的关键技术)。只不过,康托尔、哥德尔等人的对角线与蒯恩的对角线方法稍有不同。我们会在第6节中详细地讨论这些技术。
总而言之,从宗教到科学,从悖论到自复制,自指是贯穿始终的主题。正如《哥德尔、艾舍尔、巴赫》这本书指出的那样,自指是一条永恒的金带。
语言中的自指
提到自指,很多读者马上就会联系到那句臭名昭著的悖论句子:
这句话之所以让人讨厌,是因为你无论从正面(即假设它是对的),还是从反面(即假设它是错的),都会得出相反的结论。因此,这句话既不对也不错。
然而,这句“说谎者悖论”仅仅是广大自指语句家庭中的成员之一,有很多语言是自指的,但却是无害的甚至是有益的。比如下面的句子:
这句话就是一个既可以是对又可以是错的句子。你可以非常虔诚地承认这句话所论述的内容是对的,然后,再看它的内容,它正在陈述:它自己是对的。于是你初期的假设被证实了。另一方面,当你假设它是错误的时候,你就会知道它的语义“这句话对”是错误的,于是你就真的得到了这句话就是错误的结论。也就是说这句话的对错完全取决于你的假设。
当然,还有一些更好玩的自指句子,如:
这被称为自描述语句,也就是说这个句子正在描述自己的“分子”构成。当你尝试独立写下这样一个自描述语句的时候就会发现,你其实并没有创造这句话,而是这句话正在“迫使”你写出它自己。这是因为,按照这个句子的逻辑一旦你开始写下第一个字,你就必须按照已出现的字的情况而自动补全后面的句子。同时,这个语句还具有了不起的自我修复性。你不妨将该句子中的某一个汉字删掉(例如你删除第一个‘2’字),就会很快发现该句子中的一部分出现问题了,即“7个‘2’字”是错误的。因此,你会根据句子整体的意思指导而发现你少了一个‘2’字。
因此,自指不都是破坏性的,更多的自指是无害的,而且可以给我们带来一定的“惊奇性”。这种惊奇性的来源主要是自指语句中包含的无穷递归,因为它可以创造无限的虚拟层次。
虚拟层次是一个我们司空见惯的概念,例如故事中的故事,电影中的电影,梦境中的梦境等等(电影《盗梦空间》(Inception)就是对梦中梦层次的一个非常好的展示)。在上一章中,我们已经领略了程序是可以通过模拟而产生多个虚拟层次的。在语言中,我们不妨将引号看作是标识一个新的虚拟层次出现的符号。这样,下面这句话:
就包含了两个层次,更深一层的句子是“明天会下雨”,而上面一层则是“‘明天会下雨’是错的”。当然,我们通过不断地加引号就能创造出各种复杂的嵌套结构。
另外,人们发明了一类代词可以指代不同的句子。例如“这句话”,“那句话”。这些代词就仿佛是一个指针会将一个句子整体放到一个引号中而实现多个层次的嵌套。例如下面两句话:
在第一句话中出现了一个指代词“下面的句子”,它是一个指针指向了“明天会下雨”这句话,于是我们观察者作为一个解读器就会将这两句话解释为:
也就是说,我们照指代词的意思将“明天会下雨”这句话加上了引号放到了第一句中的“下面的句子”那个指代词之中了。于是,指代词创造了包含了两个虚拟层次的句子。
按照同样的逻辑,当我们遇到了指代词“这句话”的时候会发生什么呢?我们将会得到一个包含无穷虚拟层次的语句。例如我们将自指语句“这句话是错的”按照代词的法则展开就会得到:
我们看到,只要“这句话”这个指代词一出现,我们就能够得到无穷。因此,自指语句往往都与无穷虚拟层次有关。注意,我这里用的词语是“往往”,而不是“一定”。之所以这样说,是因为的确存在着一种构造自指语句的方法,让我们绕过无穷。这种方法就是大名鼎鼎的蒯恩法。
在讨论蒯恩之前,让我们先来领教句子中的动词(动词短语)。大部分动词是与我们读句子的观察者无关的,例如:
这个句子表达了小明这个人物正在做的一个动作是起床了。其中“起床了”就是一个动词。当然,有很多动词不仅可以描述一个人或者事物,还可以去描述句子,例如:
这里面的“包含5个字”就是一个描述句子“小明起床了”的动词。还有一些句子包含了动词,而这个动词是使役我们读这个句子的观察者做出某种动作的:
这个“删除第一个字”的动作就是使役读句子的观察者做出的,于是,我们按照这个句子的说法进行操作,就会得到一个新句子:
我们可以再做稍微复杂一点的操作,例如:
按照这个句子所描述的复杂操作(你最好拿来一个草稿纸,自己在纸上写一写),我们就可以得到:
好,既然你已经熟悉了这个复杂的操作,那么让我们来看下面一个古怪的句子:
如果按照这个句子指示的操作你会得到什么?让我们来做一做。按照这个句子的要求,我们可以把引号之中的句子施行下面的三步操作:第一步,把第一个字,也就是“把”放在左引号前面,这样就得到的新句子中的第一个字:“把”;第二步,将后面的字放在右引号后面,这样新句子就会以“中的第一个字放到……字不变”为结尾;第三步,保持引号和其中的字不变,于是新句子的中间会有一个引号,并且引号的中间就会是“把中的第一个字放到……”。于是,我们得到的新句子就是:
请注意,这个新句子和原句子是一模一样的!事实上,原句子使役我们观察者完成了一次对自己的拷贝!这个句子其实就是大名鼎鼎的蒯恩了!
也许,你已经有些糊涂了,让我们再好好看看究竟蒯恩是怎么操作的。首先,我们定义了一种具有动词的句子,也就是:
我们不妨将这个句子记为[math]\displaystyle{ Q(X) }[/math],其中的[math]\displaystyle{ X }[/math]就是一个空穴,可以往其中添放任何一个句子。例如,如果我们让[math]\displaystyle{ X }[/math]=“小明起床了”,那么原句子[math]\displaystyle{ Q(X) }[/math]就成为了一个完整的句子:
按照[math]\displaystyle{ Q(X) }[/math]的意思对[math]\displaystyle{ X }[/math]进行操作就得到了新句子[math]\displaystyle{ Y }[/math]:
在这个例子中,[math]\displaystyle{ Q(X) }[/math]显然与[math]\displaystyle{ Y }[/math]没有什么关系。
进一步,如果去除句子[math]\displaystyle{ Q(X) }[/math]中的空穴[math]\displaystyle{ X }[/math],我们可以得到:
它也是一个句子(尽管它不完整),我们记它为[math]\displaystyle{ Q }[/math]。最关键的时刻来临了:我们让[math]\displaystyle{ X=Q }[/math]并代入[math]\displaystyle{ Q(X) }[/math]之中会怎样?也就是将除去空穴的句子部分[math]\displaystyle{ Q }[/math]放到[math]\displaystyle{ Q(X) }[/math]这个句子的空穴[math]\displaystyle{ X }[/math]之中:
我们不妨把这个句子记做[math]\displaystyle{ Q(Q) }[/math],因为我们把空穴[math]\displaystyle{ X }[/math]换成了残句子[math]\displaystyle{ Q }[/math]。之后,我们再按照这个句子所给出的使役动词进行操作,就能得到新句子[math]\displaystyle{ Y }[/math],也就是:
令人惊奇的是,经过动词操作之后创造的句子[math]\displaystyle{ Y }[/math]与原来的句子[math]\displaystyle{ Q(Q) }[/math]竟然是一模一样的!所以句子[math]\displaystyle{ Q(Q) }[/math]利用使役动词完成了“自复制”过程,也就是[math]\displaystyle{ Q(Q)=Q(Q) }[/math]。
我们把这种技巧称之为蒯恩以纪念它的发现者美国哲学家W.V. Quine。你会看到,这种技巧可以让我们不用“这句话”指代词就能够造出自指语句,比如下面这个句子:
注意,这个句子与前面的句子稍有不同,这就是在后面加上了一个判断“得到的句子是假的”。我们不妨记[math]\displaystyle{ F= }[/math]“得到的句子是假的”,并且把:
这句话记为[math]\displaystyle{ Q^oF(X) }[/math],其中[math]\displaystyle{ ^o }[/math]符号表示将两个句子粘合在一起形成新的句子,于是[math]\displaystyle{ Q^oF(X) }[/math]就是:
我们可以验证,经过[math]\displaystyle{ Q^oF(Q^oF) }[/math]句子所描述的操作之后得到的句子跟[math]\displaystyle{ Q^oF(Q^oF) }[/math]是一模一样的。所以这句话就相当于:“这句话是假的”。我们没使用“这句话”指代词就实现了自指。
有关更多的语言中的蒯恩操作的讨论请参看《哥德尔、艾舍尔、巴赫——集异璧之大成》一书的对话《G弦上的咏叹调》,以及《Diagonalization and Self-Reference》一书。
也许你会觉得我们在玩弄语言游戏,然而,这种语言技术却在数学和计算机中起到了非常大的作用,因为蒯恩句子恰恰就是自复制机器的逻辑基础,也是Godel定理证明过程中的关键一步。下面,我们分别对建构性自指和破坏性自指进行详细地介绍。
建构性的自指
虽然提起自指,人们很容易想到自指悖轮。但是,人们不熟悉的是另外一大类无害的自指,它们通常直接应用蒯恩技术,而实现某些意想不到的结构或者功能。下面,让我们先从一种最简单的建构性自指:自打印程序说起。
所谓的程序自打印就是指一个程序能够在不读取外部文件的条件下把自己的源代码打印出来。首先,我们要先领教一下,一个自我打印的程序是多么不可能的!我们知道,要写一个程序打印出“helloworld!”字样是非常容易的,例如:
Print(‘helloworld!’)
注意在这个程序中,字符串都用单引号括起来。那么,我们能不能写一个程序,把这个打印“helloworld!”程序的源代码打印出来呢?这也是可以办到的,例如下面的程序:
Print(‘Print(\’helloworld!\’)’)
注意,这里面的“\’”会被编译器解释为一个字符串,这个字符串中就有一个字符:“ ` ”。采用这个技巧,我们就可以解决如何在一个引号之中再输入一个引号的问题了。所以,我们可以很轻松地打印出这个能够打印”helloworld!”程序的程序源代码出来。但是很显然这个程序并不能打印出它自己,也许你会想到能不能打印出上面的程序源代码出来?当然可以!
Print(‘Print(\’Print(\\\’helloworld!\\\’)\’)’)
其中\\就表示包含一个字符“\”的字符串变量,这样Print(‘\\’)就会打印出一个字符“\”,而Print(‘\\\’’)就会打印出字符串“\’”出来。所以,引号里面可以放入任意层次的引号。
但是这个程序仍然不能打印自己!你很快发现,我们人类是写不出这种能够打印自己的程序的,因为它包含了无穷递归。不过,通过蒯恩技巧,实际上我们完全可以写出来一个自打印程序,如下:
S(x){
q=’S(x){\\n q=\\\’\’+q+\’\\\’;\\n Print(\\\’\’+p(q)+\’\\\’);\\n}’;
Print(‘S(x){\n q=\’’+q+’\’;\n Print(\’’+p(q)+’\’);\n}’);
}
这里面的“\n”表示换行符,即如果执行Print(‘A\nB’),则程序会输出下面的字符串:
A B
“+”表示将两个字符串进行串联形成一个新的字符串,例如A=’123’,B=’456’,则A+B=’123456’。
这个自打印程序调用了一个简单的解码函数[math]\displaystyle{ p(q) }[/math],[math]\displaystyle{ p }[/math]的作用是将字符串[math]\displaystyle{ q }[/math]变换成更浅一层次的字符串。例如,如果[math]\displaystyle{ q }[/math]是“\\\’\\’\\n\\”,那么[math]\displaystyle{ p }[/math]这个函数就会计算输出“\’’\n\”。也就是说[math]\displaystyle{ p }[/math]完成了一组映射:它把“\\”映射成“\”,把“\’”映射成“’”,而把“\n”映射成回车符。显然[math]\displaystyle{ p }[/math]是可以写出来的。我们知道,由引号的引用可以形成更加深层次的虚拟世界(参见上一小节)。所以[math]\displaystyle{ p(q) }[/math]的作用就是让字符串[math]\displaystyle{ q }[/math]弹出一层虚拟世界。由于[math]\displaystyle{ p }[/math]的作用很简单,我们假设它是一个系统自带的函数,因此就不在源代码1中给出[math]\displaystyle{ p }[/math]的实现代码了。
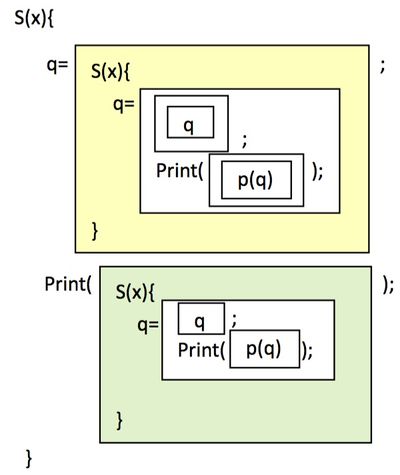
S(x)这个程序中包含了过多的“\”和“’”符号,这就导致我们理解源代码1稍显困难,下面我们将把该程序表示成下面的图,从而让读者看得更清晰一些:
如上图,这个自打印程序中的引号全部用方框来替代。这样第一层引号’…’就对应了第一层的方框,引号中的引号,即“\’…\’”就对应了框中的一个框。这样,由于程序中出现最多的层次是四层引号,即“\\\’”,所以上图中就出现了第四层框。
另外,我们还观察到,这个程序包含了两个大框,即“q=”后面的黄框和“Print()”之中的那个蓝框。这两个框的结构是完全一样的,只不过黄框比蓝框多了一个虚拟层次,这反映在所有的蓝色框中的最深一层框都再加上一层框就得到了黄色框。
更有趣的是,整个程序S(x)实际上和这两个框是相似的,因此这个程序本身就是一个分形结构。在传统的分形结构中,每一个部分都会包括无穷多的细节。但是,在这个自打印程 序中,虽然有嵌套的分形结构,但是却没有达到无穷,最深的引号也仅仅有4层。
让我们来分析一下这个程序是如何运作的。首先,看程序的最后一行,即Print(‘S(x){\nq=\’’+q+’\’;\nPrint(\’’+p(q)+’\’);\n}’);这句话的作用是让程序在屏幕上打印出一个字符串。注意观察,这个被打印出的字符串其实是由“+”号被分割成了5个部分,第一部分是“S(x){\nq=\’”,第二个部分是q这个字符串的原封不动的拷贝,第三部分是字符串:“\’;\nPrint(\’”,第四部分是函数[math]\displaystyle{ p }[/math]作用到[math]\displaystyle{ q }[/math]上面的结果即[math]\displaystyle{ p(q) }[/math];第五部分还是一个字符串:“\’);\n}”。然后当我们把q字符串的数值代入第二部分和第四部分,并进行运算[math]\displaystyle{ p }[/math]之后,就得到了和源程序一模一样的结果。你不妨在计算机上运行这段程序,就会发现这段程序会在屏幕上赤裸裸地把自己的源代码打印出来。
我们不妨把这段程序的5个部分进行归并,写成由下面的三部分构成的:[math]\displaystyle{ (Copy_o \ Popup_o \ Control) }[/math],其中Copy就是5部分中的第二部分,即相当于一个拷贝字符串的程序,你输入
给Copy什么字符串,Copy就会把那个字符串再原封不动地吐出来;Popup这部分就是原来的5部分中的第四部分,即函数[math]\displaystyle{ p }[/math],它的作用相当于一个弹出操作,也就是为输入的字符
串脱去一层引号。如果输入的字符串原来是在第[math]\displaystyle{ n }[/math]层虚拟世界,则Popup的作用就是让字符串跳到第[math]\displaystyle{ n-1 }[/math]层;最后Control这部分就相当于原来的第1、3、5这三部分以及最一开始的语句Print的总合,它的作用就相当于是为Copy和Popup制造出来的字符添加适当的连接词,使得最后的字符串能够拼接成与原来的程序一模一样的源程序,并将其打印到屏幕上。所以这句“Print(‘S(x){\nq=\’’+q+’\’;\nPrint(\’’+p(q)+’\’);\n}’);”就可以改写成[math]\displaystyle{ (Copy_o \ Popup_o \ Control)(q) }[/math]。其中“о”表示将不同的程序连接为一体。
如果我们把一个计算机程序[math]\displaystyle{ X }[/math]的描述(或者称源代码)写为[math]\displaystyle{ \lambda(X) }[/math],则自打印程序的第一条赋值语句就相当于给[math]\displaystyle{ q }[/math]赋予了[math]\displaystyle{ \lambda (Copy_o \ Popup_o \ Control) }[/math],即[math]\displaystyle{ (Copy_o \ Popup_o \ Control) }[/math]这三个程序连在一起的源代码。最后我们可以将自打印程序简写为:
S(x){
q= λ (Copyo Popupo Control)
(Copyo Popupo Control)(q);
}
我们可以进一步地把它简写为:[math]\displaystyle{ Q(q) }[/math],其中[math]\displaystyle{ Q }[/math]表示([math]\displaystyle{ (Copy_o \ Popup_o \ Control) }[/math])这三个程序的联合程序,而[math]\displaystyle{ q }[/math]则表示联合程序的源代码。[math]\displaystyle{ Q(x) }[/math]这个程序的作用是输出一个特殊的字符串“[math]\displaystyle{ X(x) }[/math]”即程序[math]\displaystyle{ X }[/math]调用自己的代码x的源程序,我们称这个[math]\displaystyle{ Q }[/math]为蒯恩函数。
那么,自打印程序不是别的,正是将蒯恩函数[math]\displaystyle{ Q }[/math]自己的源代码再喂给它自己,这样就产生了[math]\displaystyle{ Q(q)= }[/math]"[math]\displaystyle{ Q(q) }[/math]"的效果。等式左边是[math]\displaystyle{ Q }[/math]对[math]\displaystyle{ q }[/math]的计算,是一个动作,它的结果产生了等式右边的字符串"[math]\displaystyle{ Q(q) }[/math]",而这个字符串恰恰就是[math]\displaystyle{ Q }[/math]作用于[math]\displaystyle{ q }[/math]的源代码。我们看到,第2节中的蒯恩方法与这里的[math]\displaystyle{ Q(q) }[/math]是一模一样的。仔细想想不难发现,其实自打印程序的逻辑与蒯恩语句的逻辑是相通的。因此,自指恰恰就隐藏在了这段自打印程序之中了。
我们只要对这个自打印程序稍加更改就能创造出自我复制的程序出来。首先,我们要说明程序的自我复制究竟是什么意思。假设内存中漂浮着很多大大小小的程序,某一个程序P能够自我复制是指,当CPU执行到程序P的时候,P就会命令CPU执行一系列的操作使得它自己的一份拷贝会出现在内存中。但是,需要强调的是P不能够从硬盘上读取文件,否则自我复制将变得异常简单,只要把硬盘上的源程序再调用到内存中就行了。乍一看,这似乎与自打印程序一样不可能实现。但是利用与自打印程序同样的蒯恩技巧,我们依然可以很轻松地构造出自复制的程序出来。
我们只需要把自打印程序([math]\displaystyle{ (Copy_o \ Popup_o \ Control) }[/math])中的[math]\displaystyle{ Popup_o }[/math]改成Construct就可以了。这里的Construct是一个函数,你输入给Construct一段程序的源代码[math]\displaystyle{ x }[/math],它就能把[math]\displaystyle{ x }[/math]所对应的程序[math]\displaystyle{ X }[/math]编译出来并驻留在内存中。这样,程序[math]\displaystyle{ q=\lambda (Copy_o \ Popup_o \ Control) }[/math]就可以完成自复制功能。
进一步,利用同样的逻辑,我们也能够制造出可以复制自身的真实机器。只要让Construct代表从给定机器的描述[math]\displaystyle{ \lambda (X) }[/math]而构造出实际机器[math]\displaystyle{ X }[/math]就行了。在冯诺依曼的著作《自复制自动机理论(Theory of Self-reproducing Automata)》一书中,作者试图构建的自复制自动机就包括了这四个部分。即自复制机器是由一个通用拷贝机(Copy)、一个通用构造机(Construct)和一个控制器(Control)以及所有这三台机器的描述即源代码[math]\displaystyle{ q=\lambda (Copy_o \ Popup_o \ Control) }[/math]构成的。
在此小节中,我们用自打印程序和自复制程序为例来说明了建构型的自指。然而,建构性的自指实际上不仅仅是这两种,它还会有各种各样的用途。下一节,我们将介绍著名的克林尼(Kleene)的递归定理,而自打印程序和自复制程序都仅仅是递归定理的一个逻辑推论。
递归定理——一个未开采的金矿?
递归定理
首先,我们可以把上一节所论述的自打印程序稍加改动,即将源代码1中的Print改换成另外任意义个子程序F,即:
S(x){
q=’S(x){\\n q=\\\’\’+q+\’\\\’;\\n F(\\\’\’+p(q)+\’\\\’);\\n}’;
F(‘S(x){\n q=\’’+q+’\’;\n F(\’’+p(q)+’\’);\n}’);
}
然而,在这里我并没有明确定义F具体干什么,我们还必须在这段源程序后面添加上关于F这个程序的定义。比如,假设F(x)的作用就是计算字符串x的长度,并打印出来, 那么我们只要这样修改S(x)就可以了:
S(x){q=’S(x){\\n q=\\\’\’+q+\’\\\’;\\n F(\\\’\’+p(q)+\’\\\’);\\n} \\nF(x){\\n Print(length(x));\\n}’ ;
F(‘S(x){\n q=\’’+q+’\’;\n F(\’’+p(q)+’\’);\n} \nF(x){\nPrint(length(x));\n}’ );
}
F(x){
Print(length(x));
}
注意,加粗的代码部分就是在上一个代码的基础上添加的。这样,此程序不仅包含了S(x),而且还包含了一个附加的程序F(x)的定义,并且这个附加函数F(x)的源代码也需要被包含到之前F()之中和q的赋值语句之中。运行这个程序,它就会在屏幕上打印出自己源代码的长度。
也就是说源代码4这段代码实现了如下的功能:Print(length(c)),其中c就是源代码4。按照同样的方法,我们可以在自打印程序后面附加任意复杂的程序F,只要在相应的位置添加更长的字符串就行了。
不难发现,因为F可以任意地定义,所以形如代码4的计算机程序不仅可以将自己的源代码打印出来,而且还能对自己的源代码进行任意地操作F。
实际上,我们可以把上述代码总结成计算理论、递归函数论中重要的数学定理:递归定理(可以参看《Computability: an introductionto recursive function theory》一书)。在正式写出递归定理之前,我们必须先引入一些记号。
我们记[math]\displaystyle{ \phi_c }[/math]为以[math]\displaystyle{ c }[/math]为其源代码的程序,那么如果源代码为[math]\displaystyle{ c=''x+1'' }[/math],那么相应的计算机程序就是[math]\displaystyle{ \phi_{''x+1''} }[/math]。注意,区别计算机程序的源代码和计算机程序本身还是很重要的,这是因为源代码仅仅是一个字符串,而程序本身则是将源代码字符串进行编译后的可以完成某种运算的实体。另外,我们记[math]\displaystyle{ ''F(x)'' }[/math]为将程序[math]\displaystyle{ F }[/math]作用到数据[math]\displaystyle{ x }[/math]这件事的源代码。例如[math]\displaystyle{ F(x) }[/math]定义为[math]\displaystyle{ Print(x+1) }[/math],那么[math]\displaystyle{ ''F(x)'' }[/math]就是(在屏幕上打印出数字2的程序)的源代码:[math]\displaystyle{ ''Print(1+1)'' }[/math]。
有了这样一种表示方法,递归定理就可以表述为:
递归定理(也被称为Kleene第二递归定理):假设F是任意的计算机程序,那么总存在一个字符串c,使得下列等式成立1:
[math]\displaystyle{ \phi_c = \phi_{''F(c)''} }[/math] (1)
首先,等式的左边是一个计算机程序,这个程序的源代码是c。而等式的右边是另外一个计算机程序,它的源代码是任意函数F对输入变量c进行计算的编码。左边等于右边是说这两个计算机程序虽然源代码不同,但是产生的计算结果却是一模一样的。也就是无论输入给这两个程序的y是什么,[math]\displaystyle{ \phi_c }[/math],[math]\displaystyle{ \phi_{''F(c)''} }[/math]都会产生完全相同的计算结果。
我们也可以这样来理解递归定理的含义,我们知道c是左边计算机程序的源代码,而F则可以是任意一种对字符串的操作。存在某一个字符串c使得左边等于右边也就意味着存在某个计算机程序C,它可以将自己的源代码(c)进行任意地操作,即F(c)。注意在这里,我故意使用了一种“因果倒置”的解释。实际上,我们知道源代码c控制了整个计算机程序的运作,所以决定程序能将自己的源代码执行任意操作的关键因素就是c本身而并不是F(c)。但是既然c的效果和F(c)的效果是一模一样的,我们也可以把等式右侧的程序看作是起决定作用的原因而非结果,也就是程序可以对自己的源代码c进行任意的摆弄F(c),这种因果倒置的解释更容易帮助我们认识递归定理中的不平凡性。关于这种因果互换,我们还会在第8节讨论。
实际上,上一节所讲的自打印程序就是这个定理的一个特例。我们不妨设F(c)就是将c原封不动地打印到屏幕上,即Print(c),那么[math]\displaystyle{ \phi_c = \phi_{''F(c)''} }[/math] 的意思就是存在着一个程序c,执行这段c的结果(左边)就是把自己的源程序c打印到了屏幕上(右边)。即:[math]\displaystyle{ \phi_c = \phi_{''Print(c)''} }[/math] ,其中c就是上节代码1给出的自打印程序的源代码S(x)。
同样的道理,自复制的计算机程序也可以从递归定理中推论出来。只要我们令F(c)为根据代码c构造出实际的程序出来的操作Construct,那么[math]\displaystyle{ \phi_c = \phi_{''Construct(c)''} }[/math] 就意味着存在一个程序C,它可以根据自己的源代码再复制出一个程序出来。
未开采的金矿
之所以称递归定理是一个未开采的金矿,是因为定理中的程序F(x)可以是任何计算机程序。因此,只要变换F的不同形式,我们就能开发出来各种各样的应用出来。下面,我们 就来简单挖掘一下这个金矿。
自我反省的程序(Self-introspective program)
我们人类拥有的自由意识最可贵之处就在于意识可以反作用于自己,并时刻知道自己正在干什么。我们说意识具有自我反省的能力。那么,计算机程序能不能具有自我反省的能力呢?对于常见的程序来说,答案是否定的。然而,如果利用递归定理,我们便能创造出知道“自己正在干什么”的程序(具体关于自反省的程序,可以参看《Computability: an introductionto recursive function theory》一书)。
对于递归定理来说,这几乎就是小菜一碟。因为存在着这样一种计算机程序Ft(x),它的作用就是计算任意的源代码为x的程序在经过t时间步的运算后的结果以及所有中间状态(例如完成这个计算内存以及寄存器中存储的任何中间数值)。我们知道通用计算程序U(通用图灵机,参见《图灵机与计算理论》或者《Computability: an introductionto recursive function theory》)的工作原理就与这个Ft(x)类似,因为U可以模拟任意的程序X作用到任意的数据y上的结果。所以,Ft(x)的确是一个可计算的程序。
这里的t可以看作是给定的参数,因此Ft仅仅具有一个自变量,这就是源代码x。于是根据递归定理,我们便知道,存在着一个源程序c使得:
[math]\displaystyle{ \phi_c = \phi_{''F_t(c)''} }[/math] (2)
即c所对应的程序C所作的事情就是:把自己的源代码拿出来,然后在自己的虚拟机上模拟自己运算t时间步后的结果,以及当时的所有中间状态(包括内存和寄存器中的各个变量的取值)。
既然这个程序C已经清楚地了解到它自己在经过t步运算后的所有结果和中间状态了,那么我们不能说这个程序是自省的吗?所以程序也能做到知道自己正在做什么。
进化
冯诺依曼也许是最早地看到递归定理与自然进化之间存在着深刻联系的人。在他的著作《自复制自动机理论(Theory of Self-reproducing Automata)》之中,他专门探讨了由递归定理引起的自复制,以及由小的热力学涨落而作用到自复制过程中,从而可能引起的进化。
如果我们将递归定理中的程序F定义为函数Construct,即根据源代码x,构造出相应的机器Construct(x)出来,那么应用递归定理,就可以得到一个可以进行自我复制机器的源代码:λ(λ(Copyо Constructо Control)о (Copyо Constructо Control))的源代码c,使得程序运行以后,就能将自身复制。
假如,我们将程序F进行一定的修改,让它不是Construct,而是具有随机扰动的Construct,我们记为F'。F'作用到代码c上的时候,可能不会精确地制作出原始的自复制机器:λ(Copyо Constructо Control)о (Copyо Constructо Control),而是它的某种变异体。
如果这个随机变异发生在(Copyо Constructо Control)上面,那么新生成的机器就不再会有生产的功能了,因为我们已经破坏了复制的逻辑。如果变异发生在数据λ(Copyо Constructо Control)上,那么得到的新机器还具有复制的功能,但是复制的不再是它自己,而是某种变异的机器了。进一步,我们可以假设变异的可能性是在λ(Copyо Constructо Control)上面增加了一些无害的数据,例如λ(Copyо Constructо Control),那么这段数据会被(Copyо Constructо Control)执行,而形成新的机器:λ(Copyо Constructо Controlо Mutation)о (Copyо Constructо Controlо Mutation)。我们看到,这个新机器不仅没有丧失自我复制的能力,还在原来机器的基础上增加了新的功能:Mutation。如果继续运行这个变异的机器,它不仅能够自复制,而且还能将变异出来的新功能Mutation一直保持下去,直到新的变异产生。这不正是大自然的进化吗?
无穷上升的虚拟层
在上一章中我们讨论了一种可能性,就是一个计算机程序在接收外界输入的同时能够不停地构建越来越深的虚拟层次,并将自己的拷贝在这些虚拟层中不断地改造、变异。这种改造和变异可能具有非常大的任意性,从而让玩家完全不能分辨出与自己交互的究竟是原来的程序还是一个完全不同的新程序了。所以,他也就不能再分辨自己究竟是玩家还是程序员了。
也许在读上一章的时候你还对此类怪异的程序将信将疑,但是有了递归定理,我们便会看到能够产生无穷多个虚拟层,并能在每个虚拟层保持自身,同时还能根据玩家的输入而变异的程序的确是可能的。
我们可以这样来的定义递归定理中的F: F=(AcceptInputConstructо MutationоUniversalComputationConstructо Control)
也就是说这个程序F由四个部分组成,第一个部分AcceptInput可以接受外界(玩家)的输入信息;第二个部分Mutation使它可以对源代码数据进行随机变异(仿照可变异的自复制程序);第三部分UniversalComputation为一个通用计算程序(通用图灵机);第四部分Control表示为了让计算能够按照指定方式顺利运行而进行的一些控制操作。
我们看到,这个程序就能完成我们所要求的功能。首先,根据递归定理,存在着某个源程序c,使得程序C运行起来之后,它的效果等价于F这个函数作用到它自己的源代码c 上面的结果。
F将怎样作用于c呢?首先,F会调用通用计算UniversalComputation部分在运行中模拟它自己的源代码c。这也就是说程序将自己的一份源代码拷贝放置到了更深一层次的虚拟机上。同时,在每一层运行的时候,F都可以调用Mutation和AcceptInput等程序,这样系统就可以在接受玩家输入的同时不断地更改自己的源程序,从而使得输入者既是玩家又是程序员了。
总之,一旦程序可以掌握了自己的源代码,它便可以做更多的事情,而且这些事情大部分都是“自”(Self)字打头的,例如自我修复、自我调控等等。所以,递归定理可以为程序赋予真正的自我。
破坏性的自指
我们已经领教了构建性自指所创造的奇迹,下面我们会乘胜追击,继续领教破坏性自指的威力。在数理逻辑及其计算理论中,人们通常用毁灭性的自指语句(计算机程序或者字符串),也就是说谎者悖论的变种来证明某种理论的无效性。例如,最早的罗素悖论就是利用集合论的语言构造出了一种特殊的集合悖论:“不包含自己的集合”,从而反过来证明了集合论本身存在缺陷;哥德尔则通过元数学技巧构造了一个特殊的哥德尔句子“本句子在系统中不可证明”从而破灭了希尔伯特的让数学公理系统自身可以保证“完备一致性”的梦想;图灵则构造了一个特殊的程序,反驳了能够判别图灵停机问题的可能性。本小节就利用图灵停机问题和哥德尔定理为例,来说明这种毁灭性的自指是如何工作的。最后,我们将指出存在于这两种不同问题之中的共同特征。
图灵停机问题
首先,图灵停机问题的背景是来源于下列问题:我们能不能开发一个聪明的程序H,使得该程序可以读入任何一个程序X的源代码x,并判断出当程序X作用到输入字符串y上时 是否会停下来?我们可以形象地把这写程序之间的关系表达为图:
答案是,像H这样聪明的程序是不存在的,我们可以通过反证法来证明这个结论。首先,我们假设H这样的程序存在,不妨设这个程序可以写成一个二元函数:H(x,y),其中x 为程序X的源代码,y为给X输入的字符串数据,H将能判断当X作用到y上的时候是否停机。
那么,我们就可以根据H构造一个破坏性的程序D,D的定义如下:
D(z){
y=H(z,z);
If y=yes then
Do while true
Loop
Else
return
Endif
}
我们来分析一下D,它有一个输入参数z。D首先会调用H这个函数,并让H判断当源代码为z的程序Z作用到它自己源程序的字符串上是否会停下来。如果H(z,z)的返回为Yes, 也就意味着程序Z作用到自己的源代码z上会停下来,于是D开始进入一个死循环(中间的那两句:dowhiletrue…loop)。否则,D就退出去。
我们知道D是一个地道的计算机程序,没有任何毛病,只要我们能够定义出H程序,D就一定能够很好地工作。然而,当我们考虑把D作用到它自己的源代码d上的时候会怎样呢?
我们来分析一下,首先,根据D函数的定义,D会调用H函数来判断D作用到d上是否会停机。假如H函数返回的结果是Yes,即断言D作用到d上会停机,那么D这个程序就会陷入一个死循环,而永远不能停机。反过来,假如H函数返回的结果是No,即断言D作用到d上不会停机,那么D就会马上返回来,停机。因此,也不对。这样,无论H(q,q)的答案是yes还是no,都会得到矛盾的结果。于是,我们不得不放弃一开始的假设,所以H这样能判断任意的程序作用到某个数据上是否停机的程序是不存在的。
我们看到,这里面关键的一步主要在于将D这个程序作用到它自己的源代码d上的时候,这就是自指发生的时刻。无论如何,程序D(d)所发生的情形都会与H的判断正好相反, 这相当于一种二律背反,自指悖论的破坏性让我们不得不否认H函数的存在性。
让我们再回过头来分析一下D这个函数,它其实包含了两部分,第一部分是计算H(z,z)的结果,也就是判断将函数Z作用到它自身的源代码z上的时候,即Z(z)是否会停机。如果 我们将一个程序X作用到它自身的源代码x这个特殊的事件编码为"X(x)",并定义一个叫做蒯恩的计算机程序产生这样的编码,也就是定义:
那么,最终的判断H(z,z)又可以写成:H(Q(z))。所以实际上,D程序的第一部分就是将判断停机的函数H和蒯恩函数Q放到一起并同时作用到代码z上面。
程序的第二部分则是一个取反的操作,也就是如果H(z,z)判断为yes,程序就进入死循环,如果判断为no,程序就退出。而在证明的最后一步,将D作用到它的源代码d上面会产生什么情景?这个D(d)的操作恰恰能够实现自指悖论。有关图灵停机问题的详细解释请参看:图灵机与计算理论。我们将在下一小节看出这些自指技术的共同之处。
哥德尔定理2
现在让我们进入数理逻辑的领域,去领略另外一个利用破坏性自指进行的完美推理:哥德尔定理(参见:《哥德尔、艾舍尔、巴赫——集异璧之大成》和《哥德尔证明》)。
首先,我们需要简单介绍一下哥德尔定理的背景。哥德尔定理所讨论的对象是关于自然数的一套公理系统。此公理系统是由关于自然数性质的命题构成的(我们可以把这些命题简单地理解为一些合法的字符串)。例如:
[math]\displaystyle{ \forall a:\sim (a+1)=0 }[/math]
即对于任意的自然数a,a+1不为0;其中∀是任意量词,∀a就表示任意的自然数a。~表示非。再例如:
[math]\displaystyle{ \exists a \forall b \forall c:\sim a=(b+2) (c+2) }[/math]
存在着自然数a,使得对于任意给定的自然数b和c:a=(b+2)(c+2)都不成立,也就意味着存在着质数。从一组基本的语句出发(即公理,前面的第一个句子就是系统中的一个公理),按照既定的推理规则(字符串的替换规则)我们就能得到非常丰富的有关自然数的判断语句,我们称这些推导出的语句为定理。
例如下面的语句:
[math]\displaystyle{ \forall a,b: (a+b)=(a+b) }[/math]
对于任意的自然数a和b,a+b=b+a都成立,就是可以从公理中推出的定理。
另外,我们对任意一个合法的字符串都赋予一个真值,来表示该字符串所表达的语句是否为一个真的关于自然数的命题。例如,命题:
[math]\displaystyle{ \forall a,\exists b: a+b=0 }[/math]
翻译成自然语言就是:“对于任意的自然数a,都存在着一个自然数b,使得a+b=0”。那么,我们知道这个命题就是假的,这是因为我们能够举出反例,当a=1的时候,就不会存在正整数b使得a+b=0成立。而对于命题:
[math]\displaystyle{ \forall a, \exists b:\sim (a+b)=0 }[/math]
就是一个真命题。所以,我们知道:所有的系统中的合法命题都可以分成真假两类。
我们称一个公理系统是一致的,是指命题A和~A(即非A)不会同时都是该系统中的定理。这也就意味着该公理系统不包含逻辑矛盾。我们称一个公理系统是完备的,是指任意的真的命题都是该系统中的定理,也就是所有的真命题都可以通过推导而产生出来。
我们当然希望能够构建出一个足够强有力的公理系统,使得它的内部既不包含不一致的逻辑矛盾,同时又可以包含所有的关于自然数的真的命题。但是,可惜的是,哥德尔定理告诉我们,对于任何足够强有力的公理系统来说,一致性和完备性不能同时被满足。
哥德尔是如何证明这个定理的呢?关键就在于哥德尔利用这个公理系统的基本语法构建了一个哥德尔句子:
G=“我不是系统中的定理”
下面,我们就来看看究竟G是不是此公理系统中的定理?假如G是定理,也就意味着我们可以从公理出发推导出G这句话。如果接受了G,那么根据G自己的判断,G又不是系统中的定理,也就意味着系统可以得到了~G(非G)。也就是说G和~G会同时存在于系统中。于是,这意味着我们的公理系统包含着逻辑矛盾,因此该系统是不一致的。
那么,如果我们假设G不是系统中的定理呢?我们看到G就在陈述一个事实:G不是系统中的定理,而我们知道这一事实必然是真的。于是,我们得到了一个真的命题,然而此命题却并不是该系统的定理,也就是说该公理系统是不完备的。
所以,哥德尔证明了任何此类包含自然数性质的公理系统都不能同时具备一致性和完备性。
下面,我们就来看看哥德尔是如何构造出哥德尔语句G的。首先,哥德尔如何用谓词逻辑语句来表达出“是系统中的定理”这个性质的呢?
首先,我们可以将任意一个有关自然数陈述的命题编码成自然数(哥德尔配数)。例如“[math]\displaystyle{ \forall a, \exists b: \sim (a+b)=0 }[/math]”可以编码为11223......。
其次,任何一个由若干语句构成的推导过程也可以用更大的自然数来编码。例如,我们看两步推导:
[math]\displaystyle{ \forall a,\exists b:\sim (a+b)=0 }[/math]
[math]\displaystyle{ \exists b:\sim b+3=0 }[/math](将上一条语句中的任意变量a用特殊的数3来替换)
如果第一条语句的编码是11223,第二条语句的编码是23543,则这两步推导就可以表示成数字:11223023543,其中0为不同行之间的分隔符。所以自然数11223023543就唯一地表示出了一个两步的推导。
最后,我们可以用基本符号和运算构造一个命题函数(可计算函数):[math]\displaystyle{ T(m,n) }[/math],我只要把任何一个推导过程的编码[math]\displaystyle{ m }[/math]以及命题语句的编码[math]\displaystyle{ n }[/math]输入到该函数[math]\displaystyle{ T(m,n) }[/math]中,[math]\displaystyle{ T }[/math]就能够计算出该系统从公理出发,在经历了m所代表的推导过程之后就能够推导出n所代表的结论。这样,语句:
[math]\displaystyle{ \exists m:T(m,n) }[/math]
所表达的就是“n所对应的语句是该系统中的一个定理”。
接下来,我们来看这个公理系统如何表达“我”这个关键的词语。哥德尔巧妙的构造了一个自然数函数[math]\displaystyle{ Q(n) }[/math],[math]\displaystyle{ Q(n) }[/math]表达的是将[math]\displaystyle{ n }[/math]这个自然数代入到以[math]\displaystyle{ n }[/math]为编码的函数[math]\displaystyle{ N(x) }[/math]之中所得句子的哥德尔编号,也就是说[math]\displaystyle{ Q(n)=c(N,n) }[/math],其中[math]\displaystyle{ c(N,n) }[/math]为句子[math]\displaystyle{ N(n) }[/math]的哥德尔编号。
例如,考虑一个语句:
[math]\displaystyle{ \sim (a+1)=0 }[/math]
在该语句中a是一个不受任何量词约束的自由变元。假设这一公式的哥德尔编号为1199,那么将1199这个数字代入到原公式中(也就是让a=1199),就得到公式:
[math]\displaystyle{ \sim (1199+1)=0 }[/math]
假设这个新公式的哥德尔编号为3445。因此我们定义当函数[math]\displaystyle{ Q }[/math]作用到1199这个数字上面的时候就得到3445,也就是[math]\displaystyle{ Q(1199)=3445 }[/math]。注意,实际上这个[math]\displaystyle{ Q(x) }[/math]就是与上一小节中的蒯恩程序等价的蒯恩函数。
显然[math]\displaystyle{ Q }[/math]函数本身也有一个哥德尔编号,记为[math]\displaystyle{ q }[/math],那么Q(q)就是“我”的表达了,这是因为经过Q函数计算得出的数字Q(q)恰恰就是Q(q)这个公式自己的哥德尔编号。(如果不能理解这一点,请参考第2节语言的自指)
这样,我们便可以把“我”和“不是定理”连接起来构成一个新句子:
[math]\displaystyle{ Q_о T(n)= \sim \exists m:T(m,Q(n)) }[/math]
其中n为该句子中的自由变元。我们记该句子的哥德尔编号为:qоt,就可以得到哥德尔句子:
[math]\displaystyle{ G=Q_о T(q_о t)= \sim \exists m :T(m,Q(q_о t)) }[/math]
让我们来翻译一下这句话:不存在一个自然数m使得:[math]\displaystyle{ m }[/math]和[math]\displaystyle{ Q(q_о t) }[/math]构成证明对。也就是说[math]\displaystyle{ Q(q_о t) }[/math]不是系统中的定理。而[math]\displaystyle{ Q(q_о t)是什么呢?根据函数Q的定义,\lt math\gt Q(q_о t) }[/math]就是把[math]\displaystyle{ q_о t }[/math]这个数代入到[math]\displaystyle{ q_о t }[/math]所对应的语句中的自由变元之后得到的那个语句的哥德尔编码。而我们知道[math]\displaystyle{ q_о t }[/math]代入它自己[math]\displaystyle{ Q_о T(n) }[/math],并替换自由变元[math]\displaystyle{ n }[/math]之后得到的那个数就是[math]\displaystyle{ G }[/math]自己的哥德尔编号,所以[math]\displaystyle{ G }[/math]也可以翻译为:
G=“G不是一个定理”或者,干脆翻译为:
G=“我不是一个定理”。
于是,通过将蒯恩句子增加了一个“不是定理”的判断,我们便构造出类似的自指悖论出来。有关哥德尔定理的表述以及证明的细节请参考《哥德尔、艾舍尔、巴赫——集异璧之大成》一书的第十四章。
图灵停机问题与哥德尔定理之间的比较
下面,我们就来比较一下图灵停机问题以及哥德尔定理证明过程中所用到的共同的自指技巧,请看下表1。
| 编号 | 比较条目 | 图灵停机问题 | 哥德尔定理 |
|---|---|---|---|
| 1 | 基本符号 | 程序设计语言的基本符号,诸如“if then, for, loop...” | 谓词逻辑符号:“~,∧,∨,∃,∀”,算 数运算符:“+,×,=”,数字,变量等等 |
| 2 | 基本单元 | 基本符号拼接出的完整的计算机程序,例如“Print("hello world");” | 基本符号拼接出的合法的命题语句,诸 如:“∀a: ~(a+1)=0” |
| 3 | 计算 | 计算机程序对字符串操作产生新的字符串 | 命题语句根据公理和规则推导产生新的命题语句 |
| 4 | 单元编码 | 程序的源代码(字符串) | 命题的哥德尔编号 |
| 5 | 层次混淆 | 程序P去读另一个程序S的源代码s,并进行运算P(s) | 将一个命题的哥德尔编号n输入给包含自由变元的命题,并完成运算f(n) |
| 6 | 单元意义 | 程序是否停机(停或不停) | 命题是否正确(真或假) |
| 7 | 有意义的单元集合 | 所有的停机的计算机程序,数据对:(x,y)。即当x作用到y上面的时候X(y)停机 | 所有的定理,即根据公理和推理规则推 单元集合 导出的命题语句。我们希望所有的定理 都是真的(一致性),并且所有的真命题
都是定理(完备性) |
| 8 | 系统自身给出的意义判断 | H(x,y)函数:判断源代码为x的计算机程序作用到数据y上面是否停机 | 语句“∃m:T(m,n)”,即“存在一个自然数m,使得m和n构成证明对”,也就是“n所代表的命题是一个定理” |
| 9 | 蒯恩函数 | 计算机程序Q(x),定义为:让程序X读入自己的源代码,即Q(x)="X(x)" | 函数Q(n),定义为:将一个包含自由变元的语句N的编号n代入其自身的自由变元中,即 Q(n)=N(n) |
| 10 | “我” | Q(q),就是将蒯恩函数Q的源代码q(字符串)喂给函数Q它自己的代码。Q(q)为一个字符串,Q(q)="Q(q)" | Q(q),将函数Q自己的哥德尔编号q喂给函数Q。Q(q)得到的数就是它自己的哥德尔配数。Q(q)=c(Q(q))。 |
| 11 | 悖论函数 | 程序D(z),他是蒯恩程序与判断程序H(x,y)的结合,即D(z)=H(z,z)=H(Q(z)),其中z为输入的参数 | 函数QоT,也就是蒯恩函数Q(x)与意义判断语句的结合: QоT(n)=“~∃m: T(m,Q(n))”,其中 n 为一个自由变元 |
| 12 | 悖论单元 | 当程序D作用到它自己的源代码上,即D(d),表示“我不停机”。 | G,当函数QоT作用到它自己的哥德尔编码qоt上所产生的哥德尔语句即G=“~∃m:T(m,Q(qоt))”,表示“我不是定理”。注意,Q(qоt)得到的就是G的编码 |
| 13 | 二律背反 | 当H(d,d)判断D(d)停机的时候,D(d)自己的表现为不停机;而当H(d,d)判断不停机的时候,D(d)又会停机 | 当G是一个定理的时候,根据G自己的意思,G不是一个定理(破坏了一致性);当G不是一个定理的时候,我们知道G是一个真句子(破坏了完备性) |
| 14 | 结论 | 判断一切函数X作用到数据y上是否停机的计算机程序H(x,y)不存在 | 公理系统的一致性和完备性不能同时被满足 |
表1给出了图灵停机问题与哥德尔定理,以及证明这两个结论时所用的自指悖论技巧的全部细节对照表。
我们将这个对照表的不同行分成了5种颜色。首先,前四行(编号1-5)浅绿色的条目是程序系统或者公理化系统要能产生自指悖论语句所具备的基本条件和特征。我们看到,无论是计算机程序还是命题语句,它们都是由一些基本的符号拼接而成的,同时这些符号串都能够充当动词——也就是它们可以对别的符号串进行运算操作。另外,至关重要的一点是,这两个系统都能够通过编码的手段而谈论其自身。
接下来的蓝色单元格(编号6-8)表示的是系统所具备的另外一种基本属性,即意义判断。在计算机程序的世界中,我们知道程序可以分为停机的程序和不停机的程序两种;而对于命题语句来说,它们又可以分成真命题和假命题两种。这种意义判断是一个非常微妙的东西,因为,任意拿来一个程序或者是命题,我们观察者确信它们会存在着一种意义,或者是程序停机或者是命题正确。尽管在很多情况下,我们并不能马上给出这样的判断。例如,对于很复杂的程序来说,尽管我们已经等了100天,它没有停机,但是我们并不知道它会不会在第101天内停下来。但是,我们会倾向于认为任何的单元都具备某种意义或者价值,而且我们迫切地希望这种意义判断能够让系统自身告诉我们答案,也就是希望存在一个计算机程序H能够自动给出任意程序X作用到y上是否停机;或者是希望公理体系中的定理能够自动帮我们判断所有的命题是否为真,这就是语句“m:T(m,n)”的作用。尽管这个梦想最终必将破灭。我们看到,这种意义判断是破坏性自指系统特有的,而构建性自指系统不具备的重要属性之一。
其次,让我们来看黄色部分的单元格(编号9-10)。它们都是利用蒯恩技术来构建自指的核心部分。这个技术与我们前两节谈论的建构性自指部分并没有本质的区别。
然后是粉色单元格部分(编号11-13),它是破坏性自指系统的核心之处。无论是图灵停机问题还是哥德尔定理的证明,它们都用蒯恩函数加上一个否定的意义判断程序而构造了一个自指悖论出来。在图灵停机问题里面,程序D作用到自己的源代码d上面就会产生“我不会停机”的效果;而在哥德尔定理的证明中,哥德尔句子就在说“我不是一个定理”。所以D(d)和G才是整个证明中的核心。
最后,让我们来看浅蓝色的结论部分(编号14)。虽然都采用了自指悖论的技术,但是图灵停机问题的结论是否定自动意义判断程序H的存在性,而哥德尔定理则并不反对系统自身给出的意义判断语句“∃m:T(m,n)”的存在性,因为我们已经人为构造出了这样的语句,它必然是存在的,但是自指悖论引来的是这个判断语句的判断能力是受到局限的,要么它是不一致的,要么它是不完备的。看起来似乎哥德尔定理的证明与图灵停机问题的证明在这一点上很不一样,但其实如果我们仔细分析,它们仍然是相通的。假如在图灵停机问题的证明中,我们像哥德尔定理证明中一样强硬地写出来一个判断程序停机的函数H,那么同样的逻辑就会在最后一步导致这个函数H判断的局限性。也就是说对于程序D(d)来说,H是否应该判断它停机呢?如果H判断D(d)停机,那么通过分析D(d)我们知道它不会停机,也就是说H的判断会导致矛盾的结果,即不一致性。如果H判断D(d)不停机,而我们通过分析D(d)又知道它会停机,于是我们便知道H这个函数并不能将所有事实上停机的程序判断为停机,也就是说H的判断是不完备的。于是,我们便能得出与哥德尔定理类似的结论:任何判断停机问题的程序都不能同时具备一致性和完备性。
可以说,表1涵盖了所有破坏性自指中的精华。例如,我们可以用同样的方法来分析说谎者悖论:“这句话是假的”,或者等价的:
把“把中的第一个字放到左引号前面,其余的字放到右引号后面,并保持引号及其中的字不变得到的句子是假的”中的第一个字放到左引号前面,其余的字放到右引号后面,并保持引号及其中的字不变得到的句子是假的
我们可以把所有的中文句子看作是讨论的基本单元,而根据句子的动词做出的句子变换看作是基本的运算。同样句子也具备对自身操作的能力。接下来,任何一个句子的真假就是我们所说的意义判断。我们将看到,这种真假的判断只能由人来做出,而不可能由句子本身来做。证明这个结论的方法自然是构造上面那个说谎者悖论句子。在第2节的讨论中,我们已经知道,语言中也存在着蒯恩方法,即Q(X),而且把蒯恩作用到它自己上:Q(Q)就能得到完全相同的句子,即“我”:
把“把中的第一个字放到左引号前面,其余的字放到右引号后面,并保持引号及其中的字不变”中的第一个字放到左引号前面,其余的字放到右引号后面,并保持引号及其中的字不变
之后,我们将蒯恩联合上一个意义判断,即F=“得到的句子是假的”,然后将“我”即Q,与F联合起来就构成了悖论函数,即QoF(X),将悖论函数作用到它自己身上QoF(QoF)就得到了上面的那个说谎者悖论。
接下来,根据QoF(QoF),我们能得到什么结论呢?一个最简单直接的结论就是质疑:“任何句子都有对错”这个结论上,因为最后得到的悖论语句就既不真也不假。
这样,无论是程序、命题语句和自然语言,它们之中的破坏性自指现象都能得到统一。通过表1,我们还知道,不仅仅是破坏性自指现象存在着统一性,甚至构建性自指与破坏性自指一样也存在着同样的技巧,就是那个蒯恩函数和蒯恩句子。下一节,我们将把自指中的这些共同点再用“几何”的方法统一到一起。
黄金对角线3
在构建性的自指和破坏性的自指现象中,最核心的技术就是构建蒯恩函数Q(X),以及蒯恩句子Q(q)。这个蒯恩句子为什么如此重要?为什么说Q(q)就是“我”呢?这一节,我们将结合“黄金对角线”方法,从“几何表示”的角度再次审视自指。
康托尔的黄金对角线
我们这里所说的黄金对角线是一种证明方法,它起源于数学家康托尔证明实数的个数比自然数多的过程中所用的一个特殊的技巧。
首先,康托尔定义对于两个超限集合(元素个数是无穷个)A和B来说,如果能找到一个单射f:A→B(即任给一个A中的元素,都存在唯一的B中元素与其对应),那么就称A集合的元素个数c(A)<=c(B),即B集合的元素个数。反过来,如果存在单射g:B→A,那么就有c(B)<=c(A)。而如果c(A)<=c(B)和c(B)<=c(A)同时成立,就说c(B)=c(A)。
有了比较两个无穷集合元素个数的方法,我们就可以证明自然数集合N与偶数集合E的个数一样多。因为存在着单射f:N→E,f(x)=2x,同时存在单射g:E→N,g(x)=x/2。所以c(E)=c(N)。
下面,我们来比较实数集合R和自然数集合N的元素个数的多少。首先,我们很容易构造一个从N到R的单射f:N→R,f(x)=x。所以c(N)<=c(R)。
接下来,是否存在从R到N的单射呢?答案是不存在,我们可以用反证法来证明。我们可以先把问题简化,仅仅看从[0,1]这个闭区间到自然数集合N存在一个单射g。这也就意味着,对于任意的[0,1]之间的实数x,都唯一存在着一个确定的自然数n与它对应。我们称n为x的编号。我们不妨按照x的编号大小写下这些实数而形成一个表格:
| 自然数\实数位 | 1 | 2 | ...... | N | ...... |
|---|---|---|---|---|---|
| 1 | 1 | 3 | ...... | 8 | ...... |
| 2 | 2 | 7 | ...... | 6 | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
| n | 5 | 8 | ...... | 5 | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
假设我们可以将[0,1]之间的所有自然数放置到一张无穷行、无穷列的表格上。每一行就是一个实数,某一行的每一列就表示该实数小数点后面的第n位数字。例如第一个实数的第1、2、...、n、...列分别是1、3、...、8、...,那么这个小数就是0.13…8…。
下面我们考察对角线上面的元素(黄色的方格)。它表示第1个实数小数点后第一位的数字1,第2个实数小数点后第二位的数字7,...。假设第n个对角线上的数字为Q(n),那么我们构造一个特殊的数字d:
0.28….6….
也就是该数字d的第n位d(n)为:
d(n)=(Q(n)+1) mod 10
那么,很显然d是一个[0,1]之间的实数,但是d并不在表格2中,因为d的第一个位与第一个实数的第一个数字不同,所以d不是第一个数字;d的第二个位与第二个实数的第二个数字不同,所以d不是第二个数字,...。所以d肯定不在表2之中。
于是,我们便可以推知,表2并不是一张完整的从[0,1]到N的映射。存在着漏网之鱼:实数d。
不难发现,对于任意的单射g,我们总可以构造出一个对角线元素d不在表中,所以,我们只能否认一开始的假设:R与N之间存在单射。于是不可能有c(R)<=c(N),也就是实数的个数比自然数多。
康托尔的这种巧妙的对角线证明方法正是我们前面讨论的自指方法,对角线Q(n)也正是蒯恩函数,我们马上就会对此明朗了。
康托尔的黄金对角线
我们这里所说的黄金对角线是一种证明方法,它起源于数学家康托尔证明实数的个数比自然数多的过程中所用的一个特殊的技巧。
首先,康托尔定义对于两个超限集合(元素个数是无穷个)A和B来说,如果能找到一个单射f:A→B(即任给一个A中的元素,都存在唯一的B中元素与其对应),那么就称A集合的元素个数c(A)<=c(B),即B集合的元素个数。反过来,如果存在单射g:B→A,那么就有c(B)<=c(A)。而如果c(A)<=c(B)和c(B)<=c(A)同时成立,就说c(B)=c(A)。
有了比较两个无穷集合元素个数的方法,我们就可以证明自然数集合N与偶数集合E的个数一样多。因为存在着单射f:N→E,f(x)=2x,同时存在单射g:E→N,g(x)=x/2。所以c(E)=c(N)。
下面,我们来比较实数集合R和自然数集合N的元素个数的多少。首先,我们很容易构造一个从N到R的单射f:N→R,f(x)=x。所以c(N)<=c(R)。
接下来,是否存在从R到N的单射呢?答案是不存在,我们可以用反证法来证明。我们可以先把问题简化,仅仅看从[0,1]这个闭区间到自然数集合N存在一个单射g。这也就意味着,对于任意的[0,1]之间的实数x,都唯一存在着一个确定的自然数n与它对应。我们称n为x的编号。我们不妨按照x的编号大小写下这些实数而形成一个表格:
| 自然数\实数位 | 1 | 2 | ...... | N | ...... |
|---|---|---|---|---|---|
| 1 | 1 | 3 | ...... | 8 | ...... |
| 2 | 2 | 7 | ...... | 6 | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
| n | 5 | 8 | ...... | 5 | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
假设我们可以将[0,1]之间的所有自然数放置到一张无穷行、无穷列的表格上。每一行就是一个实数,某一行的每一列就表示该实数小数点后面的第n位数字。例如第一个实数的第1、2、...、n、...列分别是1、3、...、8、...,那么这个小数就是0.13…8…。
下面我们考察对角线上面的元素(黄色的方格)。它表示第1个实数小数点后第一位的数字1,第2个实数小数点后第二位的数字7,...。假设第n个对角线上的数字为Q(n),那么我们构造一个特殊的数字d:
0.28….6….
也就是该数字d的第n位d(n)为:
d(n)=(Q(n)+1) mod 10
那么,很显然d是一个[0,1]之间的实数,但是d并不在表格2中,因为d的第一个位与第一个实数的第一个数字不同,所以d不是第一个数字;d的第二个位与第二个实数的第二个数字不同,所以d不是第二个数字,...。所以d肯定不在表2之中。
于是,我们便可以推知,表2并不是一张完整的从[0,1]到N的映射。存在着漏网之鱼:实数d。
不难发现,对于任意的单射g,我们总可以构造出一个对角线元素d不在表中,所以,我们只能否认一开始的假设:R与N之间存在单射。于是不可能有c(R)<=c(N),也就是实数的个数比自然数多。
康托尔的这种巧妙的对角线证明方法正是我们前面讨论的自指方法,对角线Q(n)也正是蒯恩函数,我们马上就会对此明朗了。
程序的黄金对角线与“自我”
下面,我们将进入计算机程序的世界。首先,让我们把考虑的计算机程序设定到自然数范围内,也就是说程序F(x)中的输入x是自然数,F(x)的计算结果也是自然数。我们知道计算机程序都是有限的指令组成的字符串,于是我们可以为这些字符串编号。所以,任何程序F都对应了一个自然数编码f,而输入变量x也是自然数,我们还可以定义一个函数λ(f,x)来对程序“把数据x输入给函数F”这个事件编码,其中λ(f,t)也是一个自然数4。
既然所有程序和输入数据都编好号了,我们便可以把所有的程序针对所有的输入数据的运算情况画在下面的大表格上:
| 程序\数据 | 1 | 2 | ...... | q | ...... |
|---|---|---|---|---|---|
| 1 | λ(1,1) | λ(1,1) | ...... | λ(1,q) | ...... |
| 2 | λ(2,1) | λ(2,2) | ...... | λ(2,q) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
| q | λ(q,1) Q(1)=λ(1,1) | λ(q,2) Q(2)=λ(2,2) | ...... | λ(q,q) Q(q)=λ(q,q) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
其中,λ(n,m)就表示第n个程序计算输入数据m这个事件的编码。下面我们来考察那条黄金色的
对角线,它是第n个程序作用到它自己的编码。如果我们把这一条线上的元素都拿出来就形成了一行:
λ(1,1),λ(2,2),λ(3,3),...,λ(n,n),...
有趣的是,它的第一个元素与第一个程序作用到第一个数据上编码相同,第二个元素与第二个程序作用到第二个数据上相同,...。这一行的编码可看作一种运算Q(x):
Q(1),Q(2),Q(3),...,Q(n),...
我们只要定义程序Q为:
Q(x):=λ(x,x)
实际上Q(x)就是蒯恩函数,它作用到x上就计算出将编码为x的程序作用到x自身上这个事件的编码。这样,只要我们清晰定义了函数λ,那么Q程序就一定存在。
既然Q是可计算的,那么它必然也会占据表格中的某一行(表3中的粉色的行,设这行编码为q)。注意在这行中,我们列出了两个数值,上面的数值为程序Q作用到数据x的编码,即λ(q,x),下面的数值为函数值Q(x)=λ(x,x)。对于一般的x来说,这两个数值没什么关系。但是,粉红行与黄金对角线的交点(桔色的格子)是个意外,它的上下两个数值发生了重合。
'这个蒯恩程序所对应的行与对角线的交点是一个非常特殊的点,它就是我们前面提到的蒯恩句子,也是计算程序中的“自我”'。为什么可以这么说呢?因为程序Q作用到它自己的源代码q上的就得到了λ(q,q),即这个事件自身的编码。所以Q(q)这个计算就得到了“我”。
从这个角度看,Q(q)其实也就是那个自打印程序。只不过在自打印程序中,我们把数据q同样定义到了函数S(x)之中的q变量上。所以自打印程序S(x)其实已经包含了这个Q(q)。
同样地,Q(q)就相当于那个蒯恩句子:
把“把中的第一个字放到左引号前面,其余的字放到右引号后面,并保持引号及其中的字不变”中的第一个字放到左引号前面,其余的字放到右引号后面,并保持引号及其中的字不变
所以Q(q)神奇的地方恰恰就在于它让同样一个东西在不同的两个层次上重复了。
对角线版本的递归定理
利用对角线这种几何方法,我们同样可以说明递归定理必然成立(参看《Computability: an introductionto recursive function theory》)。首先,我们仿照表3构造另外一个表:
| 程序\数据 | 1 | 2 | ...... | v | ...... |
|---|---|---|---|---|---|
| 1 | ΦΦ1(1) | ΦΦ1(2) | ...... | ΦΦ1(v) | ...... |
| 2 | ΦΦ2(1) | ΦΦ2(2) | ...... | ΦΦ2(v) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
| v | ΦΦv(1) = ΦF(Φ1(1)) | ΦΦv(2) = ΦF (Φ2(2)) | ...... | ΦΦv(v) = ΦF(Φv(v)) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
与表3不同的地方是,此表格中的每一项不再是λ(m,n)了,而是ΦΦm(n) ,也就是第k个计算机程序Φk ,其中k为第m个程序作用到第n个数据上所计算出来的结果。如果第m个程序计算第n个数据不停机,则ΦΦm(n) 就是一个在任意输入上都没有定义的函数。因此,表中所列的不再是数,而是计算机程序本身,我们稍后将会看到这个区别的重要性。
下面,我们仍然考察那条黄金对角线,它构成了一行:
ΦΦ1(1) ,ΦΦ2(2) ,ΦΦ3(3) ,...,ΦΦn(n) ,...
接下来,我们考察任意一个计算机程序F,它可以作用到自然数:ΦΦx(x) 的计算结果上。于是我们便得到了一个复合程序FQ(x)F(x(x))。下面考察这样一个由不同的程序构成的行:
注意,这一行的每一个下标都是F作用于黄金对角线的下标的结果。这里面的每一个元素都是一个程序F(x(x))(y),其中y为该程序的输入参数,它相当于一个具有两个输入变量的程序,这样由递归函数论中的s-m-n定理(参见:《Computability: an introductionto recursive function theory》中的s-m-n定理),必然存在某一个单一输入变量的程序V(x),使得对任意的y有:
F(x(x))(y)V(x)(y)
即:
F(x(x))V(x)
那么,这个程序V(x)就必然包含在上表中的某一行(蓝色背景的那一行,假设它的行号对应为v)。我们可以断言,这一行一定与黄金对角线存在着一个交点(染成了绿色的那个格子)。
这个交点正是我们要找的满足递归定理的那一点。一方面,根据F的定义,这个交点在蓝色的行上,所以它就是一个程序F(v(v))。而另一方面,这个交点又属于黄金对角线,所以它符合对角线上的函数规则,即v(v)。同一个格子对应的显然是同一个函数,所以,必然有:
这样,我们只要取cv(v)就得到了递归定理:
cF(c)(3)
下面我们来说明为什么表4上的每一个元素是m(n)而不是n(m)。首先,我们知道n(m)是一个数即第n个程序计算第m个输入数据时候的计算结果,而m(n)是一个程序。这样,当我们说n(m)k(m)的时候仅仅意味着两个数相等,即第n个程序作用到m上的输出结果与第k个程序作用到m上的输出结果是一样的。但是这并不意味着对于任意的输入数据m都有此等式成立。
而n(m)k(m)恰恰表示计算机程序的等效。也就意味着对于任意的输入数据x来说,都有:n(m)(x)k(m)(x)。我们知道严格来说等式左边的程序编号是n(m)而右侧是k(m),这两个数字不一定相等。但是,这并不妨碍这两个程序对于所有的输入数据x的计算效果都等效。例如我们考察下面两个计算机程序:
和:
[2]ref>
很显然f(x)和g(x)是两个不同的程序,因为它们的源代码不同,这样它们的编码也必然不同。但是,我们看到这两个函数实际上是等效的,因为它们都进行x+1的计算,所以f=g是成立的。
因此,递归定理中所说的cF(c),指的就是编码为c的函数和编码为F(c)的函数等效,但这并不意味着c等于F(c)。
也许你会好奇,如果在证明递归定理的过程中,表格的所有的项目是n(m)而不是m(n)会怎样?为了满足你的好奇心,我们不妨把此表格列出:
(3)式与(1)式略有不同。(1)式为F(c)这个事件的编码,而(3)为数F(c)。但实际上,只要我们适当地选择程序F’为计算得到FQ作用到x上这个事件的编码,那么根据(3)式便能得到(1)式。所以二者实际上是等价的。
| 程序\数据 | 1 | 2 | ...... | q | ...... |
|---|---|---|---|---|---|
| 1 | λ(1,1) | λ(1,1) | ...... | λ(1,q) | ...... |
| 2 | λ(2,1) | λ(2,2) | ...... | λ(2,q) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
| q | λ(q,1) Q(1)=λ(1,1) | λ(q,2) Q(2)=λ(2,2) | ...... | λ(q,q) Q(q)=λ(q,q) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
此表与表4的不同所在是每个表项m(n)表示的是第m个程序作用到数字n上面的运算结果,而不是对此事件的编码。如果这个计算不停机,则我们可以把相应的值赋为Null。仿照表4中的推理逻辑。同样地,我们可以将黄金对角线单独列出:
1(1),2(2),...,x(x),...
然后再考虑一个任意的计算机程序F。我让它作用到这条对角线上,也就是计算F(x(x))。这可以被看作一个程序:V(x),它的编码记为v。那么它也必然在表中的某一行(蓝色的行),并且它应与黄金对角线有一个交点,我们把它染成了绿色。在这一点上,我们得到了F这个函数的一个不动点(fixedpoint),即F(c)=c,其中这个cv(v)。但是,等等,你不觉得此结论有问题吗?
我们知道F是一个任意的计算机程序,简单起见我们不妨设F(x)=x+1。那么根据刚才的推理,存在着一个数c使得F(c)=c,也就是c=c+1。注意,这里面的c是一个数,但是一个数怎么可能满足c=c+1呢?
我们得到了矛盾,哪一步出了问题?
我认为矛盾发生在空值Null上。不要忘记,表5中存在着很多空值,它表示对应的程序计算对应的数据上的时候不停机。这样,尽管程序F可以是处处定义的可计算程序,但是当它作用到不停机的程序上时,它自己也停不下来,于是也只能取空值。这样,对于某些程序F,如果找不到自然数c让F(c)=c成立的时候,就必然意味着v(v)这个计算是不停机的。
有趣的是,康托尔的证明以及下面所讲的破坏性自指的黄金对角线等方法恰恰是利用了与此类似的技巧。只不过,在那里的对角线中,我们能够事先保证v(v)是非空的数值。于是我们只能得到诸如c=c+1的矛盾,从而返回去否定前提的成立。
破坏性自指的黄金对角线
下面,我们再用“黄金对角线”,对图灵停机问题的不可解性进行两种不一样的证明。我们知道,任何计算机程序都是由一个固定的指令集中的指令组合而成的。我们还是仿照表5的方法,将所有的程序作用到所有的数据上的情况列成一张表,只不过,这张表上面的每一项不再是n(m)再是了,而是H(n,m)也就是那个能判断第n个程序作用到第m个数据上是否停机的结果。如果停机,则相应的表项就是1,否则就是0。
| 程序\数据 | 1 | 2 | ...... | q | ...... |
|---|---|---|---|---|---|
| 1 | λ(1,1) | λ(1,1) | ...... | λ(1,q) | ...... |
| 2 | λ(2,1) | λ(2,2) | ...... | λ(2,q) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
| q | λ(q,1) Q(1)=λ(1,1) | λ(q,2) Q(2)=λ(2,2) | ...... | λ(q,q) Q(q)=λ(q,q) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
其中,每一项H(m,n)就要么是0要么是1。这样,上面的黄金对角线上的数值就应该相应地取为一个01的序列,我们不妨设这个序列为:
仿照小节(1)中康托尔构造的实数d,我们可以构造这样一个“对角线删除”程序如下:
那么,这个程序D(x)所得到的计算结果就应该与对角线序列完全相反,也就是:
我们知道D(1)运算的结果与该列表中的第一行不同,D(2)与第2行不同,...,所以D(x)这个序列与列表中的每一行都不同,也就意味着D(n)这个序列不在列表中。但是,我们知道此表已经列出了所有的程序。这就得到了矛盾,于是我们得出结论,H这个函数本身的存在性应该受到质疑。
下面我们再给出另外一个图灵停机问题不可解性的证明,在这个证明中,你将能更清楚地看到对角线方法、破坏性自指、悖论之间的联系。
与以上的证明不同,我们并不直接否定掉D函数不在表6中的事实,而是假设它在该表中,并且它的编号是d,这样我们就得到了如下表格:
| 程序\数据 | 1 | 2 | ...... | q | ...... |
|---|---|---|---|---|---|
| 1 | λ(1,1) | λ(1,1) | ...... | λ(1,q) | ...... |
| 2 | λ(2,1) | λ(2,2) | ...... | λ(2,q) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
| q | λ(q,1) Q(1)=λ(1,1) | λ(q,2) Q(2)=λ(2,2) | ...... | λ(q,q) Q(q)=λ(q,q) | ...... |
| ...... | ...... | ...... | ...... | ...... | ...... |
让我们把目光锁定到蓝色的第d行。如果说D这个程序在列表中,并且d就是D的编码,那么这第d行必然会跟黄金对角线在表中有一个交点(绿色格子),按照对角线的定义法则,这个交点对应的元素必然会是H(d,d)。
但是,请不要忘记,按照D(n)这个函数的定义,D(n)=1-H(n,n),所以当n=d的时候,D(d)就应该等于1-H(d,d)。
H(d,d)与1-H(d,d)无论如何都不可能相等(注意,这里H(d,d)要么是0要么是1,绝无可能是空值)。也就是说H(d,d)说停机的时候,1-H(d,d)就说不停机,而H(d,d)说不停机的时候,1-H(d,d)就说停机。因此,我们只能得到矛盾。在整个推理的链条中,只有第一个环节,即H函数是存在的出现了问题。
实际上,这种对角线证明图灵停机问题的方法与第5节中构造自指程序的方法是相通的,尽管它们在表面上看似乎很不相同。首先,第5节中的程序D(z)实际上就是这里的程序D(n)。只不过D(z)通过判断语句和实际的死循环实现了与H(z,z)判断相反的结果,而这里的D(n)通过1-H(n,n)这样一步数学运算就实现了相同的效果。其次,在第5节中的第二步,将z=d代入D函数自己其实就相当于本节第二个方法中的对角线与蓝色的第d行的交点元素H(d,d)。最后,本节的方法1的独到之处就是在于,它直接分析D(d)这个函数计算的结果与H(1,1)不同,与H(2,2)不同,...,从而导致了D(n)不可能在列表中。以至于该方法不用分析到H(d,d)这个元素上就能完成H不存在的证明。
利用黄金对角线方法也同样可以分析哥德尔定理的证明等其它的破坏性自指现象(读者不妨分析一下如何用对角线方法来构造哥德尔定理的证明)。也就是说,黄金对角线方法与自指方法是一脉相承的;因此多书上,蒯恩函数也被称为对角线函数(例如:《Diagonalization and Self-Reference》)。
自指与观察者
本系列文章是关于观察者的,然而在这第五章中,我们一直在谈自指,却丝毫没有观察者什么事。笔者认为自指与观察者有着非常深刻的联系,而且也正是从自指的领悟中慢慢体会到观察者的作用的。我们将会看到,如果要理解自指的深层含义,观察者是必须引入的一个因素。
正如第1章所谈到的,目前的主流科学仿佛是黑色的前景,而观察者则是隐藏在白色的背景中。那么自指就位于前景与背景之间的交界处,通过自指才能从前景走到背景,也只有通过自指才能用科学的方法让观察者真正耦合到系统中。
我将分两个层次论述这个问题。首先,我们将会看到,如果想完全理解自指的含义,就必须牵扯到系统之外的观察者作用;其次,我将试图从图灵停机问题出发,指出图灵机-观 察者模型是如何将观察者作用真正地耦合到系统之中,并让它发挥普通计算机程序所不能发挥的作用的。
观察者藏于何处?
首先,在讨论自指语句,尤其是“把„„中的第一个字放在引号前面,其余的字放在引号后面„„”的时候,我曾经指出,这个句子中的动词可以使役读句子的观察者来对它进行 操作。但是,这里面的观察者引入实际上并不是必需的。因为,我们完全可以编写出一个计算机程序来操作句子,而不一定非要观察者来做。
其次,第二个可能隐藏观察者的地方就在于对“自我”的判断上。我们知道,蒯恩程序作用到自己的编码上就能够复制出一个自我出来。即Q(q)=”Q(q)”。对于计算机程序Q来说,它仅仅忠实地打印出了一个字符串“Q(q)”,这与打印出一个“Helloworld”没有什么区别。我们之所以觉得这个Q(q)程序与众不同恰恰是因为作为一个观察者,我们能够发现“Q(q)”与Q(q)的源代码是完全一样的。是观察程序运行的观察者判断出了这个Q(q)能够得到“自我”。这也与我们在第2章讨论的情形相一致,也就是说第一观察者“我”将观察箭头赋予了这个蒯恩程序Q(q),所以“自我”是被观察而出的。
但是,也许你会反驳说:“不对,这种观察能力只不过是对字符串的比较。假如我写一个程序P,它也会分析该程序的源代码是否为程序的输出。这样不需要观察者,P就可以发 现什么程序能够打印出‘自我’出来了。”真的是这样吗?我们可以利用与图灵停机问题相同的技巧来说明这样的判断程序P不可能存在。我们不妨假设P存在,它能够判断出任意源代码为x的程序X作用到数据y上产生的输出X(y)是否与自己的源代码一致。
你大概已经猜到了我将会干什么,我可以构造一个程序D(z)为:
D(z){
If P(z,z)=0 then
Return Self;
Else
Return‘ok’;
Endif
}
这个程序会来调用P这个程序,当P发现程序Z作用到数据z上面的时候得到了它自己的源代码(简写为Self),就返回一个字符串“ok”,否则将返回它自己的源代码加上数据z。P倒霉就倒霉在当把D这个程序自己的源代码d输入给D(z)它自己的时候,因为P无论怎样都一定会给出错误的判断!所以,我们只能反过头来说判断是否可以打印自身源代码的程序P不存在。
这样,一个程序是否能打印出和自己源程序一模一样的代码只能由计算机程序之外的观察者做出判断。所以,“自我”必然是被观察出来的。
另外,程序的意义也是由观察者观察出来的。在第5节的表1中,我们提到了每个程序或者是命题语句都对应了一个意义。对于程序来说,它的意义就是它是否会停机。而对于语 句来说,这个意义就是真假。正如破坏性自指所证明的,系统自身是无法既一致又完备地给出这种意义判断的。既然机械系统(计算机程序,公理系统中的定理)给不出意义判断,那么意义也仅仅能被系统之外的观察者赋予了。
为了体现出观察者才能赋予事物意义,让我们看看哥德尔语句的作用:
我不是一个定理
我们假设这句话的确不是系统的定理。那么观察者在外面就会判断这个句子的真实意义,也就是观察得出这个句子说了一个事实:它自己不是一个定理。假如没有一个观察者来观察、理解这个哥德尔语句,那么它不过就是一个普通的命题语句。如果系统推理得不到它,它也就被抛出系统了。所以,观察者在判断这个句子是一个真理的时候起到了至关重要的作用。
不仅仅是停机、或者真假等意义,几乎任何一种有意义的属性原则上讲只能由观察者做出最终的判别。比如判断一个程序是否打印了自己的源代码,判断两个程序是否完全一样等等。然而,在标准的数理逻辑、计算理论的教科书中,人们从来没有明确做出停机、真假的判断的人是系统之外的观察者。
如何利用观察者?
既然理解“自我”和程序意义的关键因素就是观察者,那么我们能否开发一种方法来系统地应用只有观察者才具备,而普通的计算机程序却没有的能力呢?答案应该是肯定的,我 们将说明利用上一章提到的图灵机-观察者模型,原则上是可以将计算机屏幕前面的观察者利用起来的。
假设观察者-图灵机模型中的图灵机就是一个可以根据某个简单特征来判断程序X作用到y上是否停机的程序H(x,y)。(例如,程序H可以简单地根据x中是否包含“do while true” 语句来粗暴地判断X(y)是否停机(输出0为不停,1为停),显然这个程序的判断是不完备的)。之后,我们便可以根据那个破坏性的自指程序D(z):=1-H(z,z),而找到一个输入d(即D的源程序)。使得这个时候H(d,d)所给出的判断与我们观察者看到的程序D(d)的行为完全相反。注意这一步的程序H和程序D都是良定义的计算机程序,可以用图灵机自动产生,完全不需要观察者的涉入。
接下来,我们知道H(d,d)一定给出一个错误的判断(根据d的定义)。但是,图灵机-观察者模型中的观察者必然能够看出D(d)究竟是否停机。根据前面的论述,观察者可以做出正确的判断。于是,我们便可以让观察者开始介入,让他手动地修改图灵机程序H为H’,使得H’(d,d)能够给出正确的判断,即D(d)是否停机。注意,此时的图灵机已经不是原来的H了,而是一个经过观察者修改的程序H’。 当然,接下来,图灵机又会根据这个新的程序H’而构造出新的程序D’,使得H’(d’,d’)总得到与真实的D’(d’)的运行情况相反的判断。于是,我们再让观察者对H’进行修改,而构造出新的程序H’’。
......
这个过程可以永远地重复下去。由于图灵停机问题的不可解性,我们可以保证这样永远重复的过程不可能被任何一个计算机程序所模拟。所以,观察者独一无二的作用便在这样一个看似机械但又不是固定的计算机程序循环中体现出来了。
因果何时逆转?
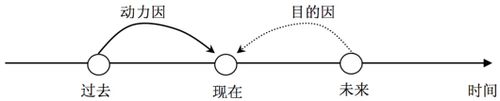
以上的讨论主要集中在破坏性的自指。而建构性的自指与观察者的结合也许能够发挥更大的作用。笔者在第2章中已经提到,生命的自主性体现为观察者观察生命的时候产生的 一种错觉:观察者会倾向于用目的因和形式因来解释被观察的生命系统,而不是用我们司空见惯的动力因和质料因。让我们把第2章的图再拷贝到这里:
这张图说明了空间上的质料因和形式因的因果箭头的逆转。我们知道任何系统在空间上都是由低层更小的元素组合而成的,例如细胞组成生物体,人组成城市。我们通常的解释是,这些微观的个体决定了整体的性质。因此我们习惯于用亚里士多德所说的质料因来解释这种因果依赖性。然而,当我们考虑生命系统的诸如自我修复特征的时候,虽然我们也可以将系统的这种能力还原到底层的质料因,但是我们通常说:“细胞自己完成了修复”,而不是说:“XX分子作用到了YY通路上,导致了ZZ生成了新的化学物质WW...”,因为后一种描述太过复杂了。所以,这时,我们用形式因代替了质料因(即右图中从上而下的虚箭头)。我们发现因果箭头从原来的自下而上转变为现在的自上而下。
同样的故事也会发生在时间上。对于通常的服从物理规律的物体来说,我们会用动力因解释它的运动,例如我们知道小球在t时刻滚到了A点是因为小球t0时刻在B点以初速度v0出发,并由于重力加速度g的作用而实现的。每时每刻,小球的过去决定了未来。但是,当我们看到一只觅食的小虫子朝向食物而去的时候,我们实际上放弃了这套熟悉的从动力因角度的解释。而是从目的因出发,也就是说小虫之所以运动到食物那里是因为小虫子“想”爬过去。或者说小虫子是有目的的前往食物那里的。所以从过去到现在的动力因因果箭头被逆转成为从未来到现在的“目的因”因果箭头。
然而,读者一定与我一样好奇,这样的因果逆转究竟是怎么发生的呢?观察者凭什么就会调转这个因果箭头呢?这些东西究竟跟自指有什么联系呢?让我们先做这样一个简单而有趣的思想试验。
假如我们能够创造这样一种完美的人类克隆体,它不仅外貌上与被克隆的人一模一样,而且能够非常完美地在瞬间模仿真人的一切动作(包括说话、运动等等)。我们假设,A和A的克隆体A’之间存在着信号传递,无论A做了什么动作,说了什么话,都可以用一个无线电装置在瞬间传递给A’,并让A’马上模仿出来。
当你看到这两个人,你如何判定它们两个哪个是真人,哪个是克隆体呢?当你面对两个一模一样的事物的时候,你会很容易发生误判。例如,你将克隆体A’误判成真实的人了。于是,你的头脑会做出这样一种解释:A’所做出的某种动作导致了A做出同样的动作。你会发现,这种假设是完全说得通的,因为A和A'的所有动作都是同时的、一模一样的,于是你既可以将A看成是原因A’是结果,你也可以将A’看成是原因A是结果。这实际上已经发生了因果的互换!我们可以这样说:完全地重合恰恰就是因果关系开始发生倒置的起点!
下面,再让我们来看自指。什么是自指?可以这样说,自指恰恰就是同样一个事物在不同的层次上发生了完美的重合。所以,不同层次的同一事物就会表现给观察者完全一样的动作和过程,这个时候,观察者也就不能够分辨出哪一个是因,哪一个是果了。自指让观察者心智中的因果箭头开始发生倒置。
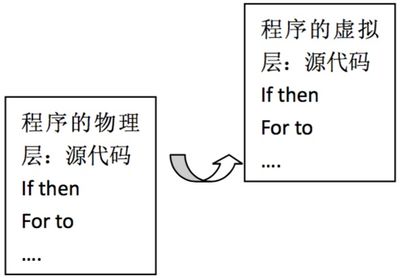
让我们以自我反省的程序为例说明。我们知道,自我反省的程序包括两个层次,一个是它的“物理层”也就是由我们设计者写好的源代码。另一个层次则是由这个计算机程序动态 运行生成的“虚拟层”。而这个程序正在进行反省,也就是意味着该程序正在虚拟层模拟它自己在物理层上的动作,如图:
由于程序将自己的源代码原封不动地拷贝到了虚拟层,并进行分析、模拟,所以我们观察者将会看到两个不同层次完美的重合。当程序不仅仅做出分析,而且还能够做出输入输出响应的时候,我们将会看到和刚才的假想实验相似的情况:不知情的观察者将会发生混淆,以至于既可以把程序物理层的源代码看作是原因,也有可能将程序的虚拟层的源代码看作是原因。这就使得因果倒置成为了可能。假如虚拟层的程序比物理层的程序跑得更快些(虚拟层的程序跑了T步,而物理层的程序仅仅跑了t步,其中T>t),那么观察者将更可能认为这个程序的虚拟层“控制”了物理层的部分,于是程序按照“自己”的意愿完成了动作。这和观察者看到一个小虫可以朝向食物自主的运动是完全同样的道理。
不仅仅是自我反省的程序,我们会看到任何一个具备构建型自指能力的系统都包括了两层次,而且是同一个东西在不同的层次实现了重合。例如,我们考察自打印程序,这个程序实际上是三个不同层次的两两重合。第一层是该程序内部包含的数据:λ((Copyо Popupо Control)),第二个层次是该程序内部的实体结构:(Copyо Popupо Control)。首先,这两层其实是同一个东西的再现,即都是(Copyо Popupо Control),它们完成了一次重合。
另外,我们考察另外两个层面,与自我反省的程序类似,一个层面是该程序的物理层,也就是整个源代码:λ((Copyо Popupо Control))о (Copyо Popupо Control)。另一个是它运行之后在屏幕上打印出来的东西,即仍然是这个源代码自己。这两个层次发生了重合。
这种不同层次的融合也发生在对角线证明方法之中。我们看表3。粉色的格子上面一行是程序Q所得到的运算结果;下面一行是表格的排列规则;当两者重合在桔黄色的那个方 格,即那个蒯恩句子,或者是“自我”点的时候,程序自身做出的判断与表格的排列发生了完美的重合!
让我们更加引申一层,其实生命的奥妙并不在于多么复杂的物理规则,也不在于多么精巧的控制逻辑,其本质就在于自指在不同层面的重合。当这种重合发生的时候,信息与物理完全同构、未来与过去完全同构、真实与虚拟完全同构、甚至观察者与被观察物从某种意义上说也完全同构!所以,重要的并不是我们人类如何有意识地去认识、理解、掌控这个物质 世界,而是如何效仿、模拟、同构我们所处的环境,因为奇迹就发生在重合与同构当中。
小结
本章将20世纪30年代人们通过数理逻辑、计算理论对自指问题的认识进行了比较详细的综述,并重点指出了人们不太熟悉的构建性自指问题。最后,我们又将自指问题在观察者 理论中的重要性突出出来。可以说,自指问题恰恰是前景主流科学和背景观察者理论的交叉边界之处。所以,从科学的角度认识观察者的性质是与自指问题密不可分的。本章我们将观察者理论的不同应用融入到了各个章节之中,其中包括无穷上升的虚拟层次,图灵机-观察者模型解决停机问题,因果倒置与生命的本质等等。
然而,我认为这些讨论还是不够全面的。我们在本章忽略的主要问题就是概率因素。可以说只有建立在概率和随机体系下的科学理论才是现代的科学理论。我们如何将概率因素融入到自指问题之中呢?我们是否可以讨论随机的自指问题,随机的判定问题?进一步,我们将如何把第3章和第4章谈到的量子概率方法融入到自指体系当中?我个人强烈地以为自指悖论中的二律悖反性质恰恰是量子概率最好的用武之地。
我认为这些都是未来研究的重要理论问题。