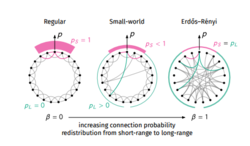
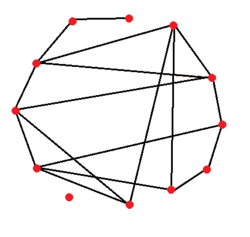
ER随机图模型

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
费米子（讨论 | 贡献）2020年4月28日 (二) 16:15的版本 （→‎历史）
跳到导航 跳到搜索

在图论的数学理论部分中，ER随机图模型 Erdős–Rényi model可指代两个密切相关的随机图生成模型中的任意一个。ER随机图模型的名字源于最早提出上述模型之一的数学家保尔•厄多斯 Paul Erdős和阿尔弗烈德•瑞利 Alfréd Rényi，他们在1959年首次提出了其中一个模型，[1][2]而几乎在同时期，埃德加•吉尔伯特 Edgar Gilbert独立提出了另外一个模型。[3]在Erdős和Rényi的模型中，节点集一定、连边数也一定的所有图是等概率的；在Gilbert的模型中，每个连边存在与否有着固定的概率，与其他连边无关。在概率方法中，这两种模型可用来证明满足各种性质的图的存在，也可为几乎所有图的性质提供严格的定义。

定义

ER随机图模型有两个密切相关的版本。

  • 在模型[math]\displaystyle{ G(n,M) }[/math]中，从[math]\displaystyle{ n }[/math]个节点、[math]\displaystyle{ M }[/math]个连边构成的所有图的集合里随机选择一个图。例如，在[math]\displaystyle{ G(3, 2) }[/math]模型中，3个节点和2个连边能构成三种可能的图，每种图的概率为1/3。
  • 在模型[math]\displaystyle{ G(n,p) }[/math]中，随机连接节点构成一个图。图中每个连边彼此独立，连接的概率为[math]\displaystyle{ p }[/math]。等价地，拥有[math]\displaystyle{ n }[/math]个节点、[math]\displaystyle{ M }[/math]个连边的所有图具有相同的概率：
[math]\displaystyle{ p^M (1-p)^{{n \choose 2}-M} }[/math]


此模型中的参数[math]\displaystyle{ p }[/math]可以看成是加权函数；随着[math]\displaystyle{ p }[/math]从0增加到1，模型更倾向于包含拥有更多连边的图，而包含拥有较少连边的图的概率则降低。特别地，与[math]\displaystyle{ p=0.5 }[/math]相对应的情况是，在拥有[math]\displaystyle{ n }[/math]个节点的[math]\displaystyle{ 2^\binom{n}{2} }[/math]个图中，每个图被选择的概率相等。


我们通常研究节点数[math]\displaystyle{ n }[/math]趋于无穷时随机图的表现。尽管在这种情况下，[math]\displaystyle{ p }[/math]和[math]\displaystyle{ M }[/math]可以固定，但是，它们也可以是关于[math]\displaystyle{ n }[/math]的函数。例如，命题“[math]\displaystyle{ G(n, 2ln(n)/n) }[/math]中几乎每个图都是连通的”的意思是，当[math]\displaystyle{ n }[/math]趋于无穷时，拥有[math]\displaystyle{ n }[/math]个节点、连边概率为[math]\displaystyle{ 2ln(n)/n }[/math]的图连通的概率趋于1。

两种模型的比较

二项分布ER模型生成的一个图[math]\displaystyle{ （p=0.01） }[/math]

[math]\displaystyle{ G(n,p) }[/math]中可能的连边数为[math]\displaystyle{ \binom{n}{2}p }[/math]，由大数定律，[math]\displaystyle{ G(n,p) }[/math]中的每个图几乎必有大概这么多连边（假设可能的连边数趋于无穷）。因此，粗略的结果是如果[math]\displaystyle{ pn^2 →∞ }[/math]，那么当[math]\displaystyle{ M=\tbinom{n}{2} p }[/math]随着[math]\displaystyle{ n }[/math]的增加而增加时，[math]\displaystyle{ G(n,p) }[/math]将与[math]\displaystyle{ G(n,M) }[/math]有相似的表现。许多图的性质都是这样。如果P是满足对子图序单调的任意一种图的性质（即若[math]\displaystyle{ A }[/math]是[math]\displaystyle{ B }[/math]的子图且[math]\displaystyle{ A }[/math]满足[math]\displaystyle{ P }[/math]，则[math]\displaystyle{ B }[/math]也满足[math]\displaystyle{ P }[/math]），那么命题“[math]\displaystyle{ G(n,p) }[/math]中几乎所有图满足[math]\displaystyle{ P }[/math]”等价于“[math]\displaystyle{ G(n, \tbinom{n}{2} p) }[/math]中几乎所有图满足[math]\displaystyle{ P }[/math]”（其中[math]\displaystyle{ pn^2 →∞ }[/math]）。


例如，当[math]\displaystyle{ P }[/math]是连通性时，或[math]\displaystyle{ P }[/math]是包含哈密顿圈的性质时，上述关系就成立。然而，它对非单调性质（如具有偶数连边的性质）未必成立。


如今在实际应用中，[math]\displaystyle{ G(n,p) }[/math]模型更加常用，部分原因是通过连边的独立性进行分析较为容易。

[math]\displaystyle{ G(n,p) }[/math]的性质

沿用上述符号，[math]\displaystyle{ G(n,p) }[/math]中的一个图平均有[math]\displaystyle{ \binom{n}{2}p }[/math]条连边。任意特定节点的度服从二项分布：[4]

[math]\displaystyle{ P(\deg(v) = k) = {n-1\choose k}p^k(1-p)^{n-1-k}, }[/math]

其中n为图中节点的总数。由于

[math]\displaystyle{ P(\deg(v) = k) \to \frac{(np)^k \mathrm{e}^{-np}}{k!} \quad \text{ as } n \to \infty \text{ and } np = \text{ constant }, }[/math]

故当[math]\displaystyle{ n }[/math]很大且[math]\displaystyle{ np= }[/math]常数时，服从泊松分布。


在1960年的一篇论文中，Erdős和Rényi[5]非常精确地描述了p在不同取值下[math]\displaystyle{ G(n, p) }[/math]的表现。其结论有：

  • 若[math]\displaystyle{ np\lt 1 }[/math]，则[math]\displaystyle{ G(n,p) }[/math]中的一个图几乎一定没有连通分量的大小大于[math]\displaystyle{ O(log(n)) }[/math]。
  • 若[math]\displaystyle{ np=1 }[/math]，则[math]\displaystyle{ G(n,p) }[/math]中的一个图几乎必有最大的连通分量，其阶为[math]\displaystyle{ n^{2/3} }[/math]。
  • 若[math]\displaystyle{ np→c\gt 1 }[/math]，其中[math]\displaystyle{ c }[/math]为常数，则[math]\displaystyle{ G(n,p) }[/math]中的一个图几乎必有唯一的包含节点有限部分的巨连通集团。没有连通分量会有超过[math]\displaystyle{ O(log(n)) }[/math]个节点。
  • 若[math]\displaystyle{ p\lt \tfrac{(1-\varepsilon)\ln n} n }[/math]，则[math]\displaystyle{ G(n,p) }[/math]中的一个图几乎必有孤立节点，因而它是不连通的。
  • 若 [math]\displaystyle{ p{\gt }\tfrac{(1+\varepsilon)\ln n} n }[/math]，则[math]\displaystyle{ G(n,p) }[/math]中的一个图几乎一定是连通的。

因此[math]\displaystyle{ \tfrac{\ln n} n }[/math]是[math]\displaystyle{ G(n,p) }[/math]连通性的重要临界值。


当[math]\displaystyle{ n }[/math]趋于无穷大时，还有许多图的性质几乎处处成立。例如，存在[math]\displaystyle{ k(n) }[/math]（近似等于[math]\displaystyle{ 2log^2(n) }[/math]）使得[math]\displaystyle{ G(n,0.5) }[/math]中最大团的大小几乎必为[math]\displaystyle{ k(n) }[/math]或[math]\displaystyle{ k(n)+1 }[/math]。[6]


因此，尽管确定图中最大团的大小是NP完全的，但“典型”图中最大团的大小（根据此模型）是非常好理解的。 ER图的连边对偶图是几乎有着相同度分布的图，但具有度相关性，且集聚系数更高。[7]

与渗流的关系

在渗流理论中，人们研究有限或无限的图，并随机删除连边（或连接）。因此，ER模型的过程实际就是完全图上未加权连接的渗流。（所谓渗流，就是在加权的情况下以不同的权重移除节点和（或）连边）。渗流理论有很深的物理学根源，大部分研究都是在欧几里得空间中的格子上进行的。[math]\displaystyle{ np=1 }[/math]时，由巨连通分量向小连通分量的转变与这些图类似，但对格子来说，确定临界点很难。物理学家通常将对完全图的研究称为平均场理论，因此ER模型的过程就是渗流的平均场情况。


人们在随机图的渗流上也做了许多重要研究。从物理学家的角度看，这仍是一个平均场模型，所以它常被看成一个通信网络，研究结果常用图的鲁棒性来表示。设一个随机图有[math]\displaystyle{ n\gt \gt 1 }[/math]个节点，平均度为[math]\displaystyle{ \lt k\gt }[/math]。从网络中随机删除[math]\displaystyle{ 1-p' }[/math]个节点，仅保留一部分[math]\displaystyle{ p' }[/math]。存在渗流临界值[math]\displaystyle{ p'_c=\tfrac{1}{\langle k\rangle} }[/math]，使得低于该值时，网络变得支离破碎，而高于[math]\displaystyle{ p'_c }[/math]时，会有[math]\displaystyle{ n }[/math]阶巨连通分量存在。巨连通分量的相对大小[math]\displaystyle{ P_∞ }[/math]由下式给出:[5][1][2][8]

[math]\displaystyle{ P_\infty= p'[1-\exp(-\langle k \rangle P_\infty)]. \, }[/math]

说明

[math]\displaystyle{ G(n,p) }[/math]模型的两个主要假设（连边独立，每条连边可能性相同）可能不适合为某些现实生活中的现象建模。尤其是ER图的度分布没有厚尾，而许多实际网络的分布是厚尾的。此外，与许多社交网络不同，ER图集聚系数较低。其他较好的替代模型可见BA网络模型 Barabási–Albert model和WS小世界网络模型 Watts and Strogatz model。这两个替代模型不是渗流过程，它们分别是生长模型和断边重连模型。布尔德列夫 Buldyrev等人最近又设计了一种用于交互的ER随机图模型。[9]

历史

1959年，Edgar Gilbert在研究之前提到的连通性临界值的论文中，首次引入了[math]\displaystyle{ G(n,p) }[/math]模型。[3][math]\displaystyle{ G(n,M) }[/math]模型则是Erdős和Rényi在他们1959年的论文中提出来的。与Gilbert一样，他们首先研究的是[math]\displaystyle{ G(n, M) }[/math]的连通性，1960年，他们做了更详细的分析。

另请参阅

  • 拉多图 Rado graph，将[math]\displaystyle{ G(n,p) }[/math]模型扩展到可数无穷个顶点的图。与有限的情况不同，这种趋于无穷过程的结果（概率为1）是相同的图，直到同构。
  • 双相演化 Dual-phase evolution 描述了与ER模型相关的性质推动系统中秩序出现的方式。
  • 指数随机图 Exponential random graph models 描述的是给定网络统计数据和各种相关参数的“n”节点图的一般概率分布。
  • 随机分块模型 Stochastic block model ，是ER模型的推广，是具有潜在社团结构的图。
  • WS小世界模型
  • BA网络模型

参考文献

  1. ↑ 1.0 1.1 Erdős, P.; Rényi, A. (1959). "On Random Graphs. I" (PDF). Publicationes Mathematicae. 6: 290–297.
  2. ↑ 2.0 2.1 Bollobás, B. (2001). Random Graphs (2nd ed.). Cambridge University Press. ".ISBN 0-521-79722-5" 
  3. ↑ 3.0 3.1 E.N. Gilbert (1959). "Random Graphs". Annals of Mathematical Statistics. 30 (4): 1141–1144. .doi:10.1214/aoms/1177706098 {{cite journal}}: External link in |last= and |quote= (help)
  4. ↑ Newman, Mark. E. J.; Strogatz, S. H.; Watts, D. J. (2001). "Random graphs with arbitrary degree distributions and their applications". Physical Review E. 64: 026118. arXiv:cond-mat/0007235. Bibcode:2001PhRvE..64b6118N. doi:10.1103/PhysRevE.64.026118. PMID 11497662., Eq. (1)
  5. ↑ 5.0 5.1 Erdős, P.; Rényi, A. (1960). "On the evolution of random graphs" (PDF). Magyar Tudományos Akadémia Matematikai Kutató Intézetének Kőzleményei [Publications of the Mathematical Institute of the Hungarian Academy of Sciences]. 5: 17–61. 这里的概率p指的是[math]\displaystyle{ N(n) = \tbinom{n}{2} p }[/math]
  6. ↑ Matula, David W. (February 1972). "The employee party problem". Notices of the American Mathematical Society. 19: A-382.
  7. ↑ Ramezanpour, A.; Karimipour, V.; Mashaghi, A. (April 2003). "Generating correlated networks from uncorrelated ones". Physical Review E. 67 (4): 046107. arXiv:cond-mat/0212469. Bibcode:2003PhRvE..67d6107R. doi:10.1103/PhysRevE.67.046107. PMID 12786436.
  8. ↑ Bollobás, B.; Erdős, P. (1976). "Cliques in Random Graphs". Mathematical Proceedings of the Cambridge Philosophical Society. 80 (3): 419–427. Bibcode:1976MPCPS..80..419B. doi:10.1017/S0305004100053056.
  9. ↑ Buldyrev, S. V.; Parshani, R.; Paul, G.; Stanley, H. E.; Havlin, S. (2010). "Catastrophic cascade of failures in interdependent networks". Nature. 464 (7291): 1025–8. arXiv:0907.1182. Bibcode:2010Natur.464.1025B. doi:10.1038/nature08932. PMID 20393559.


进一步阅读

编者推荐

文献推荐

一种接近ER随机图的小世界网络模型

一种接近ER随机图的小世界网络模型

著名的Watts-Strogatz小世界网络模型并未接近总随机化极限的Erdos-Renyi随机图模型，这可能导致混淆并使某些分析复杂化。本文提出了一个简单的替代方案，它不是重连，而是在具有基于距离的连接概率的节点对之间绘制边，并证明了这个模型更容易分析并接近相应极限中的真正的Erdos-Renyi随机图模型。给出了关于度分布，度方差，每个节点的两个星数，每个节点的三角形数，聚类系数和随机游走混合时间的分析结果。


基于Chung-Lu随机图模型生成大规模无标度网络

通过生成随机图模型和可伸缩算法生成综合网络是网络分析中的一个经常性使用的工具，它为实际网络中各种属性的统计分析提供了一个有根据的基础。本文用Chung－Lu模型说明了如何生成具有幂律分布的大型随机图。此外，这篇文章提供了模型参数的显式公式，以便生成满足对最小、最大和平均期望度的行为的若干要求，并且具有若干期望特性的随机图，包括具有任意指定指数大于2的幂律度分布，存在一个巨大的组件并且没有潜在的孤立节点。


随机图 (平均度2.833 平均最短路径长度2.109 聚类系数0.167)

课程推荐

复杂的网络与优雅的几何

本课程沿着几何的线路重新梳理复杂网络，包括ER随机网、小世界网络、无标度网络，网络的分形特征等。之后，该课程重点讲述如何利用真实的网络数据来重构系统的空间几何特征。


本中文词条由普天星相用户参与编译，Flynn审校，张江总审校，乐多多编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=ER随机图模型&oldid=5610”