Lotka–Volterra方程式

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

25px  此article介紹的是the predator-prey equations。For the competition equations, see Competitive Lotka–Volterra equations.

Numbers of snowshoe hare (yellow, background) and Canada lynx (black line, foreground) furs sold to the Hudson's Bay Company. Canada lynxes eat snowshoe hares.

snowshoe hare (yellow, background) and Canada lynx (black line, foreground) furs sold to the Hudson's Bay Company. Canada lynxes eat snowshoe hares.]]

雪鞋兔(黄色，背景)和加拿大猞猁(黑线，前景)毛皮出售给哈德逊湾公司。加拿大猞猁吃雪鞋兔[]

The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:

The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:

Lotka-Volterra 方程又称捕食-食饵方程，是一对一阶非线性微分方程，常用于描述两种群相互作用的生物系统的动力学行为。人口随时间变化，根据这一对方程:

[math]\displaystyle{ \lt math\gt 数学 \begin{align} \begin{align} Begin { align } \frac{dx}{dt} &= \alpha x - \beta x y, \\ \frac{dx}{dt} &= \alpha x - \beta x y, \\ 阿尔法 x-贝塔 x y \frac{dy}{dt} &= \delta x y - \gamma y, \frac{dy}{dt} &= \delta x y - \gamma y, X y-γ y, \end{align} \end{align} end { align } }[/math]

</math>

数学

where

where

在哪里

x is the number of prey (for example, rabbits);

is the number of prey (for example, rabbits);

是猎物的数量(例如，兔子) ;

y is the number of some predator (for example, foxes);

is the number of some predator (for example, foxes);

是某种捕食者(例如狐狸)的数量;

[math]\displaystyle{ \tfrac{dy}{dt} }[/math] and [math]\displaystyle{ \tfrac{dx}{dt} }[/math] represent the instantaneous growth rates of the two populations;

[math]\displaystyle{ \tfrac{dy}{dt} }[/math] and [math]\displaystyle{ \tfrac{dx}{dt} }[/math] represent the instantaneous growth rates of the two populations;

Math 和 math 表示两个种群的瞬时增长率;

t represents time;

represents time;

代表时间;

α, β, γ, δ are positive real parameters describing the interaction of the two species.

are positive real parameters describing the interaction of the two species.

是描述两个物种相互作用的正实参数。

The Lotka–Volterra system of equations is an example of a Kolmogorov model, which is a more general framework that can model the dynamics of ecological systems with predator–prey interactions, competition, disease, and mutualism.

The Lotka–Volterra system of equations is an example of a Kolmogorov model, which is a more general framework that can model the dynamics of ecological systems with predator–prey interactions, competition, disease, and mutualism.

Lotka-沃尔泰拉方程组就是 Kolmogorov 模型的一个例子，该模型是一个更为通用的框架，可以为具有捕食者-食饵相互作用、竞争、疾病和互利共生的生态系统的动态建模。

History

The Lotka–Volterra predator–prey model was initially proposed by Alfred J. Lotka in the theory of autocatalytic chemical reactions in 1910. This was effectively the logistic equation, originally derived by Pierre François Verhulst. In 1920 Lotka extended the model, via Andrey Kolmogorov, to "organic systems" using a plant species and a herbivorous animal species as an example and in 1925 he used the equations to analyse predator–prey interactions in his book on biomathematics. The same set of equations was published in 1926 by Vito Volterra, a mathematician and physicist, who had become interested in mathematical biology. Volterra's enquiry was inspired through his interactions with the marine biologist Umberto D'Ancona, who was courting his daughter at the time and later was to become his son-in-law. D'Ancona studied the fish catches in the Adriatic Sea and had noticed that the percentage of predatory fish caught had increased during the years of World War I (1914–18). This puzzled him, as the fishing effort had been very much reduced during the war years. Volterra developed his model independently from Lotka and used it to explain d'Ancona's observation.

The Lotka–Volterra predator–prey model was initially proposed by Alfred J. Lotka in the theory of autocatalytic chemical reactions in 1910. This was effectively the logistic equation, originally derived by Pierre François Verhulst. In 1920 Lotka extended the model, via Andrey Kolmogorov, to "organic systems" using a plant species and a herbivorous animal species as an example and in 1925 he used the equations to analyse predator–prey interactions in his book on biomathematics. The same set of equations was published in 1926 by Vito Volterra, a mathematician and physicist, who had become interested in mathematical biology. Volterra's enquiry was inspired through his interactions with the marine biologist Umberto D'Ancona, who was courting his daughter at the time and later was to become his son-in-law. D'Ancona studied the fish catches in the Adriatic Sea and had noticed that the percentage of predatory fish caught had increased during the years of World War I (1914–18). This puzzled him, as the fishing effort had been very much reduced during the war years. Volterra developed his model independently from Lotka and used it to explain d'Ancona's observation.

洛特卡-沃尔泰拉捕食-被捕食模型最初是由阿尔弗雷德 · j · 洛特卡于1910年在自催化化学反应理论中提出的。这实际上就是逻辑方程式，最初由皮埃尔·弗朗索瓦·韦吕勒推导出来。1920年，Lotka 通过安德雷·柯尔莫哥洛夫，将这个模型扩展到“有机系统” ，以植物物种和草食动物物种为例，1925年，他在其关于生物数学的书中用这些方程分析了捕食者-猎物的相互作用。1926年，对数学生物学感兴趣的数学家和物理学家维托 · 沃尔泰拉发表了同样的方程组。沃尔泰拉的调查灵感来自于他与海洋生物学家翁贝托•安科纳(Umberto d’ ancona)的互动。安科纳当时正在追求自己的女儿，后来成了他的女婿。D’ ancona 研究了亚得里亚海的鱼类捕获量，并注意到在第一次世界大战期间(1914-1918年)捕获的捕食性鱼类的百分比有所增加。这使他感到困惑，因为在战争年代，捕鱼的努力大大减少了。沃尔泰拉独立于 Lotka 发展了他的模型，并用它来解释 d’ ancona 的观察。

The model was later extended to include density-dependent prey growth and a functional response of the form developed by C. S. Holling; a model that has become known as the Rosenzweig–MacArthur model. Both the Lotka–Volterra and Rosenzweig–MacArthur models have been used to explain the dynamics of natural populations of predators and prey, such as the lynx and snowshoe hare data of the Hudson's Bay Company and the moose and wolf populations in Isle Royale National Park.

The model was later extended to include density-dependent prey growth and a functional response of the form developed by C. S. Holling; a model that has become known as the Rosenzweig–MacArthur model. Both the Lotka–Volterra and Rosenzweig–MacArthur models have been used to explain the dynamics of natural populations of predators and prey, such as the lynx and snowshoe hare data of the Hudson's Bay Company and the moose and wolf populations in Isle Royale National Park.

该模型后来被扩展到包括密度依赖的猎物生长和由 C.s. 霍林开发的功能性反应形式，这个模型后来被称为 Rosenzweig-MacArthur 模型。Lotka-Volterra 模型和 Rosenzweig-MacArthur 模型都被用来解释捕食者和猎物的自然种群动态，例如哈德逊湾公司的猞猁和雪鞋兔的数据，以及皇家岛国家公园的驼鹿和狼的种群数据。

In the late 1980s, an alternative to the Lotka–Volterra predator–prey model (and its common-prey-dependent generalizations) emerged, the ratio dependent or Arditi–Ginzburg model. The validity of prey- or ratio-dependent models has been much debated.

In the late 1980s, an alternative to the Lotka–Volterra predator–prey model (and its common-prey-dependent generalizations) emerged, the ratio dependent or Arditi–Ginzburg model. The validity of prey- or ratio-dependent models has been much debated.

在20世纪80年代后期，出现了一种替代 Lotka-沃尔泰拉捕食者-被捕食者模型(及其普通-被捕食者依赖的一般化)的模型，即比率依赖模型或 Arditi-Ginzburg 模型。食饵或比率依赖模型的有效性一直备受争议。

The Lotka–Volterra equations have a long history of use in economic theory; their initial application is commonly credited to Richard Goodwin in 1965 or 1967.

The Lotka–Volterra equations have a long history of use in economic theory; their initial application is commonly credited to Richard Goodwin in 1965 or 1967.

洛特卡-沃尔泰拉方程在经济理论中的应用由来已久，它们最初的应用通常归功于1965年或1967年的理查德•古德温(Richard Goodwin)。

Physical meaning of the equations

The Lotka–Volterra model makes a number of assumptions, not necessarily realizable in nature, about the environment and evolution of the predator and prey populations:

The Lotka–Volterra model makes a number of assumptions, not necessarily realizable in nature, about the environment and evolution of the predator and prey populations:

Lotka-Volterra 模型对捕食者和被捕食者种群的环境和进化做出了许多假设，但这些假设在自然界中不一定是可实现的:

1. The prey population finds ample food at all times.

The prey population finds ample food at all times.

猎物总能找到充足的食物。

1. The food supply of the predator population depends entirely on the size of the prey population.

The food supply of the predator population depends entirely on the size of the prey population.

捕食者种群的食物供应完全取决于猎物种群的大小。

1. The rate of change of population is proportional to its size.

The rate of change of population is proportional to its size.

人口的变化率与其规模成正比。

1. During the process, the environment does not change in favour of one species, and genetic adaptation is inconsequential.

During the process, the environment does not change in favour of one species, and genetic adaptation is inconsequential.

在这个过程中，环境并没有因为一个物种而改变，基因的适应也是无关紧要的。

1. Predators have limitless appetite.

Predators have limitless appetite.

食肉动物有无限的食欲。

As differential equations are used, the solution is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.

As differential equations are used, the solution is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.

由于微分方程的使用，解是确定的和连续的。反过来，这意味着捕食者和被捕食者的世代是不断重叠的。

See also: Competitive Lotka–Volterra equations

Prey

When multiplied out, the prey equation becomes

When multiplied out, the prey equation becomes

当它们相乘时，食饵方程就变成了

[math]\displaystyle{ \frac{dx}{dt} = \alpha x - \beta x y. }[/math]

[math]\displaystyle{ \frac{dx}{dt} = \alpha x - \beta x y. }[/math]

数学 frac { dt } alpha x beta x y

The prey are assumed to have an unlimited food supply and to reproduce exponentially, unless subject to predation; this exponential growth is represented in the equation above by the term αx. The rate of predation upon the prey is assumed to be proportional to the rate at which the predators and the prey meet, this is represented above by βxy. If either x or y is zero, then there can be no predation.

The prey are assumed to have an unlimited food supply and to reproduce exponentially, unless subject to predation; this exponential growth is represented in the equation above by the term αx. The rate of predation upon the prey is assumed to be proportional to the rate at which the predators and the prey meet, this is represented above by βxy. If either or is zero, then there can be no predation.

被捕食者被假定有无限的食物供应并且以指数形式繁殖，除非被捕食; 这个指数增长在上面的方程中用术语 x 来表示。捕食食物的速率被假定为与捕食者和猎物相遇的速率成正比，这在上面用 xy 表示。如果其中一个或者等于零，那么就不存在捕食。

With these two terms the equation above can be interpreted as follows: the rate of change of the prey's population is given by its own growth rate minus the rate at which it is preyed upon.

With these two terms the equation above can be interpreted as follows: the rate of change of the prey's population is given by its own growth rate minus the rate at which it is preyed upon.

有了这两个项，上面的公式可以解释为: 猎物种群的变化率是由它自己的增长率减去它被捕食的速率。

Predators

The predator equation becomes

The predator equation becomes

捕食者方程变成了

[math]\displaystyle{ \frac{dy}{dt} = \delta xy - \gamma y. }[/math]

[math]\displaystyle{ \frac{dy}{dt} = \delta xy - \gamma y. }[/math]

Delta xy-gamma y / math

In this equation, δxy represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used, as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). γy represents the loss rate of the predators due to either natural death or emigration, it leads to an exponential decay in the absence of prey.

In this equation, δxy represents the growth of the predator population. (Note the similarity to the predation rate; however, a different constant is used, as the rate at which the predator population grows is not necessarily equal to the rate at which it consumes the prey). γy represents the loss rate of the predators due to either natural death or emigration, it leads to an exponential decay in the absence of prey.

在这个方程中，xy 表示捕食者种群的增长。(注意与捕食率的相似性; 然而，使用了一个不同的常数，因为捕食者种群增长的速度不一定等于它消耗猎物的速度)。Y 代表食肉动物因自然死亡或移居海外而损失的比率，在没有猎物的情况下，y 代表指数衰减。

Hence the equation expresses that the rate of change of the predator's population depends upon the rate at which it consumes prey, minus its intrinsic death rate.

Hence the equation expresses that the rate of change of the predator's population depends upon the rate at which it consumes prey, minus its intrinsic death rate.

因此这个方程表达了捕食者种群数量的变化率取决于捕食的速率减去其固有的死亡率。

Solutions to the equations

The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions, although they are quite tractable.

The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions, although they are quite tractable.

这些方程有周期解，并且没有用通常的三角函数表示的简单表达式，尽管它们很容易处理。

If none of the non-negative parameters α, β, γ, δ vanishes, three can be absorbed into the normalization of variables to leave only one parameter: since the first equation is homogeneous in x, and the second one in y, the parameters β/α and δ/γ are absorbable in the normalizations of y and x respectively, and γ into the normalization of t, so that only α/γ remains arbitrary. It is the only parameter affecting the nature of the solutions.

If none of the non-negative parameters vanishes, three can be absorbed into the normalization of variables to leave only one parameter: since the first equation is homogeneous in , and the second one in , the parameters β/α and δ/γ are absorbable in the normalizations of and respectively, and into the normalization of , so that only remains arbitrary. It is the only parameter affecting the nature of the solutions.

如果所有的非负参数都不消失，三个参数可以被吸收到变量的归一化中，只留下一个参数: 因为第一个方程是齐次方程，第二个方程是齐次方程，所以这些参数 / 和 / 可以分别被和的正规化和归一化所吸收，所以只能是任意的。这是影响解的性质的唯一参数。

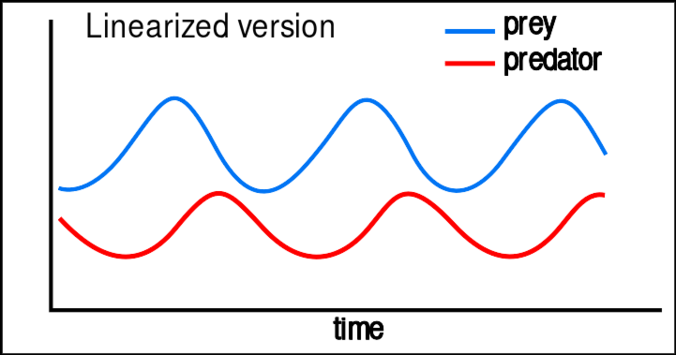
A linearization of the equations yields a solution similar to simple harmonic motion with the population of predators trailing that of prey by 90° in the cycle.

A linearization of the equations yields a solution similar to simple harmonic motion with the population of predators trailing that of prey by 90° in the cycle.

方程的一个线性化得到了一个类似于简谐运动的解决方案，在这个周期中捕食者的数量尾随猎物的数量达到90。

center

中心

A simple example

Population dynamics for baboons and cheetahs problem mentioned aside.

Population dynamics for baboons and cheetahs problem mentioned aside.

除了狒狒和猎豹的族群动态问题。

Phase-space plot for the predator prey problem for various initial conditions of the predator population.

Phase-space plot for the predator prey problem for various initial conditions of the predator population.

捕食者种群不同初始条件下捕食与被捕食问题的相空间情节。

Suppose there are two species of animals, a baboon (prey) and a cheetah (predator). If the initial conditions are 10 baboons and 10 cheetahs, one can plot the progression of the two species over time; given the parameters that the growth and death rates of baboon are 1.1 and 0.4 while that of cheetahs are 0.1 and 0.4 respectively. The choice of time interval is arbitrary.

Suppose there are two species of animals, a baboon (prey) and a cheetah (predator). If the initial conditions are 10 baboons and 10 cheetahs, one can plot the progression of the two species over time; given the parameters that the growth and death rates of baboon are 1.1 and 0.4 while that of cheetahs are 0.1 and 0.4 respectively. The choice of time interval is arbitrary.

假设有两种动物，狒狒(猎物)和猎豹(捕食者)。如果初始条件是10只狒狒和10只猎豹，人们可以绘制出这两个物种随着时间的推移的进展情况; 假定参数是狒狒的生长率和死亡率分别为1.1和0.4，而猎豹的生长率和死亡率分别为0.1和0.4。时间间隔的选择是任意的。

One may also plot solutions parametrically as orbits in phase space, without representing time, but with one axis representing the number of prey and the other axis representing the number of predators for all times.

One may also plot solutions parametrically as orbits in phase space, without representing time, but with one axis representing the number of prey and the other axis representing the number of predators for all times.

人们也可以在相空间中将解参数化地绘制成轨道，但不代表时间，而是用一个轴代表猎物的数量，另一个轴代表捕食者的数量。

This corresponds to eliminating time from the two differential equations above to produce a single differential equation

This corresponds to eliminating time from the two differential equations above to produce a single differential equation

这相当于从上面的两个微分方程中消除时间，得到一个微分方程

[math]\displaystyle{ \frac{dy}{dx} = - \frac{y}{x} \frac{\delta x - \gamma}{\beta y -\alpha} }[/math]

[math]\displaystyle{ \frac{dy}{dx} = - \frac{y}{x} \frac{\delta x - \gamma}{\beta y -\alpha} }[/math]

数学 frac { dx }- frac { delta x- gamma }{ beta y- alpha } / math

relating the variables x and y. The solutions of this equation are closed curves. It is amenable to separation of variables: integrating

relating the variables x and y. The solutions of this equation are closed curves. It is amenable to separation of variables: integrating

关联变量 x 和 y。这个方程的解是封闭曲线。它可以通过分离变量法: 集成

[math]\displaystyle{ \frac{\beta y - \alpha}{y} \,dy + \frac{\delta x - \gamma}{x} \,dx = 0 }[/math]

[math]\displaystyle{ \frac{\beta y - \alpha}{y} \,dy + \frac{\delta x - \gamma}{x} \,dx = 0 }[/math]

数学[ beta y-alpha ][ y ][ y ][ y ][ y ][ y ][ y ][ y ][ y ][ y ]

yields the implicit relationship

yields the implicit relationship

产生了隐含的关系

[math]\displaystyle{ V = \delta x - \gamma \ln(x) + \beta y - \alpha \ln(y), }[/math]

[math]\displaystyle{ V = \delta x - \gamma \ln(x) + \beta y - \alpha \ln(y), }[/math]

数学 v delta x- gamma ln (x) + beta y- alpha ln (y) ，/ math

where V is a constant quantity depending on the initial conditions and conserved on each curve.

where V is a constant quantity depending on the initial conditions and conserved on each curve.

其中 v 是一个常量，取决于初始条件，在每条曲线上都是守恒的。

An aside: These graphs illustrate a serious potential problem with this as a biological model: For this specific choice of parameters, in each cycle, the baboon population is reduced to extremely low numbers, yet recovers (while the cheetah population remains sizeable at the lowest baboon density). In real-life situations, however, chance fluctuations of the discrete numbers of individuals, as well as the family structure and life-cycle of baboons, might cause the baboons to actually go extinct, and, by consequence, the cheetahs as well. This modelling problem has been called the "atto-fox problem", an atto-fox being a notional 10⁻¹⁸ of a fox.

An aside: These graphs illustrate a serious potential problem with this as a biological model: For this specific choice of parameters, in each cycle, the baboon population is reduced to extremely low numbers, yet recovers (while the cheetah population remains sizeable at the lowest baboon density). In real-life situations, however, chance fluctuations of the discrete numbers of individuals, as well as the family structure and life-cycle of baboons, might cause the baboons to actually go extinct, and, by consequence, the cheetahs as well. This modelling problem has been called the "atto-fox problem", an atto-fox being a notional 10⁻¹⁸ of a fox.

旁白: 这些图表说明了作为生物模型的一个严重的潜在问题: 对于这个特定的参数选择，在每个周期中，狒狒的数量减少到极低的数量，然后恢复(而猎豹的数量在狒狒密度最低时仍然相当可观)。然而，在现实生活中，不连续的个体数量的偶然波动，以及狒狒的家庭结构和生命周期，可能会导致狒狒实际上灭绝，结果，猎豹也会灭绝。这个建模问题被称为“ atto-fox 问题” ，一个 atto-nowiki fox / nowiki 是一个概念上的10 sup-18 / sup of a fox。

Phase-space plot of a further example

文件:Lotka-Volterra orbits 01.svg

300x300px

A less extreme example covers:

300x300pxA less extreme example covers:

300x300pxA 不那么极端的例子包括:

α = 2/3, β = 4/3, γ = 1 = δ. Assume x, y quantify thousands each. Circles represent prey and predator initial conditions from x = y = 0.9 to 1.8, in steps of 0.1. The fixed point is at (1, 1/2).

= 2/3,  = 4/3,  = 1 = . Assume  quantify thousands each. Circles represent prey and predator initial conditions from  =  = 0.9 to 1.8, in steps of 0.1. The fixed point is at (1, 1/2).

= 2/3,  = 4/3,  = 1 = .假设每个数量都是成千上万。圆圈表示猎物和捕食者的初始条件从0.9到1.8，步长为0.1。定点在(1,1 / 2)。

Dynamics of the system

In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a cycle of growth and decline.

In the model system, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and decline. As the predator population is low, the prey population will increase again. These dynamics continue in a cycle of growth and decline.

在模型系统中，当猎物数量充足时，捕食者就会兴旺发达，但最终食物供应不足，食物减少。当捕食者数量较少时，猎物数量又会增加。这些动态在增长和衰退的循环中继续。

Population equilibrium

Population equilibrium occurs in the model when neither of the population levels is changing, i.e. when both of the derivatives are equal to 0:

Population equilibrium occurs in the model when neither of the population levels is changing, i.e. when both of the derivatives are equal to 0:

人口均衡发生在模型中，当两个人口水平都没有变化时，即。当两个导数都等于0时:

[math]\displaystyle{ x(\alpha - \beta y) = 0, }[/math]

[math]\displaystyle{ x(\alpha - \beta y) = 0, }[/math]

数学 x ( alpha- beta y)0 / math

[math]\displaystyle{ -y(\gamma - \delta x) = 0. }[/math]

[math]\displaystyle{ -y(\gamma - \delta x) = 0. }[/math]

数学 y ( gamma- delta x)0. / math

The above system of equations yields two solutions:

The above system of equations yields two solutions:

上述方程组得出两个解:

[math]\displaystyle{ \{y = 0,\ \ x = 0\} }[/math]

[math]\displaystyle{ \{y = 0,\ \ x = 0\} }[/math]

数学，数学

and

and

及

[math]\displaystyle{ \left\{y = \frac{\alpha}{\beta},\ \ x = \frac{\gamma}{\delta} \right\}. }[/math]

[math]\displaystyle{ \left\{y = \frac{\alpha}{\beta},\ \ x = \frac{\gamma}{\delta} \right\}. }[/math]

数学左边，左边，左边，右边，数学

Hence, there are two equilibria.

Hence, there are two equilibria.

因此，有两个均衡。

The first solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zero numbers, and, in the simplified model, do so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters α, β, γ, and δ.

The first solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zero numbers, and, in the simplified model, do so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters α, β, γ, and δ.

第一个解决方案有效地代表了这两个物种的灭绝。如果两个种群都是0，那么它们将无限期地保持这种状态。第二个解表示一个固定点，在这个固定点上，两个种群都维持它们当前的非零数，并且在简化模型中，无限期地这样做。实现这种平衡的人口水平取决于参数、、和的选择值。

Stability of the fixed points

The stability of the fixed point at the origin can be determined by performing a linearization using partial derivatives.

The stability of the fixed point at the origin can be determined by performing a linearization using partial derivatives.

原点不动点的稳定性可以通过用偏导数进行线性化来确定。

The Jacobian matrix of the predator–prey model is

The Jacobian matrix of the predator–prey model is

该模型的雅可比矩阵为

[math]\displaystyle{ J(x, y) = \begin{bmatrix} \lt math\gt J(x, y) = \begin{bmatrix} 数学 j (x，y) begin { bmatrix } \alpha - \beta y & -\beta x \\ \alpha - \beta y & -\beta x \\ 阿尔法贝塔 n-贝塔 \delta y & \delta x - \gamma \delta y & \delta x - \gamma 三角洲 y 三角洲 x 三角洲伽玛 \end{bmatrix}. }[/math]

\end{bmatrix}.</math>

{ bmatrix } . / math

and is known as the community matrix.

and is known as the community matrix.

被称为社区矩阵。

First fixed point (extinction)

When evaluated at the steady state of (0, 0), the Jacobian matrix J becomes

When evaluated at the steady state of (0, 0), the Jacobian matrix J becomes

当求解稳态(0,0)时，雅可比矩阵 j 变为

[math]\displaystyle{ J(0, 0) = \begin{bmatrix} \lt math\gt J(0, 0) = \begin{bmatrix} 数学 j (0,0) begin { bmatrix } \alpha & 0 \\ \alpha & 0 \\ 阿尔法和0 0 & -\gamma 0 & -\gamma 0 & gamma \end{bmatrix}. }[/math]

\end{bmatrix}.</math>

{ bmatrix } . / math

The eigenvalues of this matrix are

The eigenvalues of this matrix are

这个矩阵的特征值是

[math]\displaystyle{ \lambda_1 = \alpha, \quad \lambda_2 = -\gamma. }[/math]

[math]\displaystyle{ \lambda_1 = \alpha, \quad \lambda_2 = -\gamma. }[/math]

数学1阿尔法，数学2-伽玛

In the model α and γ are always greater than zero, and as such the sign of the eigenvalues above will always differ. Hence the fixed point at the origin is a saddle point.

In the model α and γ are always greater than zero, and as such the sign of the eigenvalues above will always differ. Hence the fixed point at the origin is a saddle point.

在模型中和总是大于零，因此上面的特征值的符号总是不同的。因此原点的不动点是鞍点。

The stability of this fixed point is of significance. If it were stable, non-zero populations might be attracted towards it, and as such the dynamics of the system might lead towards the extinction of both species for many cases of initial population levels. However, as the fixed point at the origin is a saddle point, and hence unstable, it follows that the extinction of both species is difficult in the model. (In fact, this could only occur if the prey were artificially completely eradicated, causing the predators to die of starvation. If the predators were eradicated, the prey population would grow without bound in this simple model.) The populations of prey and predator can get infinitesimally close to zero and still recover.

The stability of this fixed point is of significance. If it were stable, non-zero populations might be attracted towards it, and as such the dynamics of the system might lead towards the extinction of both species for many cases of initial population levels. However, as the fixed point at the origin is a saddle point, and hence unstable, it follows that the extinction of both species is difficult in the model. (In fact, this could only occur if the prey were artificially completely eradicated, causing the predators to die of starvation. If the predators were eradicated, the prey population would grow without bound in this simple model.) The populations of prey and predator can get infinitesimally close to zero and still recover.

这个不动点的稳定性具有重要意义。如果它是稳定的，可能会吸引非零种群，因此，在许多初始种群水平的情况下，系统的动态可能导致两个物种的灭绝。然而，由于原点的不动点是鞍点，因此是不稳定的，因此在模型中两个物种的灭绝都是困难的。(事实上，只有当猎物被人为地完全消灭，导致捕食者饿死时，才会发生这种情况。在这个简单的模型中，如果捕食者被消灭，猎物的数量就会无限增长捕食者和被捕食者的数量可以无限小地接近于零，并且仍然可以恢复。

Second fixed point (oscillations)

Evaluating J at the second fixed point leads to

Evaluating J at the second fixed point leads to

在第二个固定点上对 j 进行评估将导致

[math]\displaystyle{ J\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) = \begin{bmatrix} \lt math\gt J\left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) = \begin{bmatrix} 数学 j 左( frac { gamma { delta } ， frac { alpha }右) begin { bmatrix } 0 & -\frac{\beta \gamma}{\delta} \\ 0 & -\frac{\beta \gamma}{\delta} \\ 0 & frac { beta gamma }{ delta } \frac{\alpha \delta}{\beta} & 0 \frac{\alpha \delta}{\beta} & 0 Frac { alpha delta } beta } & 0 \end{bmatrix}. }[/math]

\end{bmatrix}.</math>

{ bmatrix } . / math

The eigenvalues of this matrix are

The eigenvalues of this matrix are

这个矩阵的特征值是

[math]\displaystyle{ \lambda_1 = i \sqrt{\alpha \gamma}, \quad \lambda_2 = -i \sqrt{\alpha \gamma}. \lt math\gt \lambda_1 = i \sqrt{\alpha \gamma}, \quad \lambda_2 = -i \sqrt{\alpha \gamma}. 数学第一道程序，第二道程序。 }[/math]

</math>

数学

As the eigenvalues are both purely imaginary and conjugate to each others, this fixed point is elliptic, so the solutions are periodic, oscillating on a small ellipse around the fixed point, with a frequency [math]\displaystyle{ \omega = \sqrt{\lambda_1 \lambda_2} = \sqrt{\alpha \gamma} }[/math] and period [math]\displaystyle{ T = 2{\pi}/(\sqrt{\lambda_1 \lambda_2}) }[/math].

As the eigenvalues are both purely imaginary and conjugate to each others, this fixed point is elliptic, so the solutions are periodic, oscillating on a small ellipse around the fixed point, with a frequency [math]\displaystyle{ \omega = \sqrt{\lambda_1 \lambda_2} = \sqrt{\alpha \gamma} }[/math] and period [math]\displaystyle{ T = 2{\pi}/(\sqrt{\lambda_1 \lambda_2}) }[/math].

由于特征值都是纯虚的，并且彼此共轭，这个不动点是椭圆的，所以解是周期性的，振荡在一个小椭圆上围绕着不动点，具有频率 math-λ-λ-λ-λ-λ-λ-λ-gamma / math 和 period-λ-λ-λ-λ-λ-λ-λ-λ-λ。

As illustrated in the circulating oscillations in the figure above, the level curves are closed orbits surrounding the fixed point: the levels of the predator and prey populations cycle and oscillate without damping around the fixed point with frequency [math]\displaystyle{ \omega = \sqrt{\alpha \gamma} }[/math].

As illustrated in the circulating oscillations in the figure above, the level curves are closed orbits surrounding the fixed point: the levels of the predator and prey populations cycle and oscillate without damping around the fixed point with frequency [math]\displaystyle{ \omega = \sqrt{\alpha \gamma} }[/math].

如上图中循环振荡所示，水平曲线是围绕不动点的闭合轨道: 捕食者和被捕食者种群的水平周期在不动点周围振荡而没有阻尼。

The value of the constant of motion V, or, equivalently, K = exp(V), [math]\displaystyle{ K = y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} }[/math], can be found for the closed orbits near the fixed point.

The value of the constant of motion V, or, equivalently, K = exp(V), [math]\displaystyle{ K = y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} }[/math], can be found for the closed orbits near the fixed point.

运动常数 v 的值，或者等价地，k exp (v) ，math k y ^ α ^ γ ^ e ^ {-△ x } / math，可以在不动点附近的闭合轨道上找到。

Increasing K moves a closed orbit closer to the fixed point. The largest value of the constant K is obtained by solving the optimization problem

Increasing K moves a closed orbit closer to the fixed point. The largest value of the constant K is obtained by solving the optimization problem

增 k 使闭合轨道更接近于固定点。常数 k 的最大值是通过求解最佳化问题得到的

[math]\displaystyle{ y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} = \frac{y^\alpha x^\gamma}{e^{\delta x+\beta y}} \longrightarrow \max\limits_{x,y\gt 0}. }[/math]

[math]\displaystyle{ y^\alpha e^{-\beta y} x^\gamma e^{-\delta x} = \frac{y^\alpha x^\gamma}{e^{\delta x+\beta y}} \longrightarrow \max\limits_{x,y\gt 0}. }[/math]

数学 y ^ alpha ^ e ^-beta y } x ^ gamma ^-delta x ^ alpha ^ gamma } e ^ delta x + beta y } longtarrow max limits { x，y 0} . / math

The maximal value of K is thus attained at the stationary (fixed) point [math]\displaystyle{ \left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) }[/math] and amounts to

The maximal value of K is thus attained at the stationary (fixed) point [math]\displaystyle{ \left(\frac{\gamma}{\delta}, \frac{\alpha}{\beta}\right) }[/math] and amounts to

因此，k 的最大值可以在静止(不动)点的左(frac { gamma { delta } ，frac { alpha }{ beta }右) / math 上求得，达到

[math]\displaystyle{ K^* = \left(\frac{\alpha}{\beta e}\right)^\alpha \left(\frac{\gamma}{\delta e}\right)^\gamma, }[/math]

[math]\displaystyle{ K^* = \left(\frac{\alpha}{\beta e}\right)^\alpha \left(\frac{\gamma}{\delta e}\right)^\gamma, }[/math]

数学 k ^ 左( frac { beta e }右) ^ alpha 左( frac { delta e }右) ^ gamma，/ math

where e is Euler's number.

where e is Euler's number.

其中 e 是欧拉数。

See also

• Competitive Lotka–Volterra equations

• Generalized Lotka–Volterra equation

• Mutualism and the Lotka–Volterra equation

• Community matrix

• Population dynamics

• Population dynamics of fisheries

• Nicholson–Bailey model

• Reaction–diffusion system

• Paradox of enrichment

• Lanchester's laws, a similar system of differential equations for military forces

References

• Leigh, E. R. (1968). "The ecological role of Volterra's equations". Some Mathematical Problems in Biology.  – a modern discussion using Hudson's Bay Company data on lynx and hares in Canada from 1847 to 1903.

• Kaplan, Daniel; Glass, Leon (1995). Understanding Nonlinear Dynamics. New York: Springer. ISBN 978-0-387-94440-1. https://archive.org/details/understandingnon0000kapl. 

• Murray, J. D. (2003). Mathematical Biology I: An Introduction. New York: Springer. ISBN 978-0-387-95223-9. 

• Yorke, James A.; Anderson, William N. Jr. (1973). "Predator-Prey Patterns (Volterra-Lotka equations)" (PDF). PNAS. 70 (7): 2069–2071. doi:10.1073/pnas.70.7.2069. JSTOR 62597. PMID 16592100.

• Llibre, J.; Valls, C. (2007). "Global analytic first integrals for the real planar Lotka-Volterra system". J. Math. Phys. 48 (3): 033507. doi:10.1063/1.2713076.

External links

• From the Wolfram Demonstrations Project — requires CDF player (free):

• • Predator–Prey Equations

• • Predator–Prey Model

• • Predator–Prey Dynamics with Type-Two Functional Response

• • Predator–Prey Ecosystem: A Real-Time Agent-Based Simulation

• Lotka-Volterra Algorithmic Simulation (Web simulation).

Category:Predation

类别: 掠夺

Category:Ordinary differential equations

类别: 常微分方程

Category:Fixed points (mathematics)

类别: 定点(数学)

Category:Population models

类别: 人口模型

Category:Mathematical modeling

类别: 数学建模

Category:Community ecology

类别: 群落交错区

This page was moved from wikipedia:en:Lotka–Volterra equations. Its edit history can be viewed at Lotka–Volterra方程式/edithistory