混沌理论

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索


值[math]\displaystyle{ r = 28,σ=10, b=8/3 }[/math]的Lorenz吸引子图
中等能量的双杆摆表现出混沌行为。从稍微不同的初始条件开始摆动会导致一个完全不同的轨迹。双杆摆是最简单的具有混沌解的动力系统之一

混沌理论 Chaos theory是数学的一个分支，主要研究动力系统的混沌状态，其表面无序和不规则的随机状态往往受到对初始条件高度敏感的确定性规律的支配。[1][2]混沌理论是一个跨学科的理论，表明，在混沌复杂系统的明显随机性，有潜在的模式，相互联系，不断的反馈循环，重复，自相似，分形和自我组织。[3] 蝴蝶效应，一个基本的混沌原理，描述了如何在一个确定性非线性的一个状态的微小变化可以导致大的差异在后来的状态(意味着有对初始条件的敏感依赖)。[4]这种行为的一个隐喻是，一只蝴蝶在中国扇动它的翅膀可以引起德克萨斯州的飓风。


初始条件中的微小差异，例如数值计算中的舍入误差，可能导致此类动力系统的结果差异很大，使得对其行为的长期预测通常是不可能的。[5]即使这些系统是确定性的，这意味着它们未来的行为遵循一个独特的演变[6]，完全由它们的初始条件决定，没有任何随机因素参与。[7]换句话说，这些系统的确定性本质并不能使它们具有可预测性。[8][9]这种行为被称为确定性混沌，或简单的混沌。爱德华·洛伦茨 Edward Lorenz将这一理论总结为:[10]


混乱：当当前决定未来时，但是近似当前并不能近似确定未来。


混沌现象存在于许多自然系统中，包括流体流动、心跳异常、天气和气候。[11][12][6]社会学、物理学、[13] 环境科学、计算机科学、工程学、经济学、生物学、生态学和哲学。该理论为复杂动力系统、混沌边缘理论和自组织过程等领域的研究奠定了基础。


引言

混沌理论关注确定性系统，其行为原则上可以预测。混沌系统在一段时间内是可以预测的，然后“显现”成为随机的。一个混沌系统的行为能够被有效预测的时间取决于三个因素: 预测中能够容忍的不确定性有多大，其当前状态能够被测量的有多准确，以及一个取决于系统动力学的时间尺度，称为李雅普诺夫时间 Lyapunov time。李雅普诺夫时间的一些例子是: 混沌电路，大约1毫秒; 天气系统，几天(未经证实) ; 内太阳系，400万到500万年。[14]在混沌系统中，预报中的不确定性随着时间的流逝呈指数增长。因此，从数学上来说，预测时间要比预测中比例不确定性的平方多一倍。这意味着，在实践中，一个有意义的预测不能超过两到三倍的李雅普诺夫时间间隔。当不能做出有意义的预测时，系统就会显得随机。[15]


混沌动力学

由x → 4 x (1 – x) and y → (x + y) mod 1 定义的映射显示对初始 x 位置的灵敏度。在这里，两组 x 和 y 值随着时间的推移从一个微小的初始差异显著分化。

在通常的用法中，“混沌”意味着“无序的状态”。[16][17]然而，在混沌理论中，这个术语的定义更为精确。尽管没有一个被广泛接受的关于混沌的数学定义，一个最初由Robert l. Devaney提出的常用定义认为，要把动力系统分类为混沌，它必须具备以下特性:[18]

  1. 它必须对初始条件很敏感,
  2. 必须具有拓扑传递性,
  3. 它一定有密集的周期轨道。

在某些情况下，上面提到的最后两个性质实际上暗示了对初始条件的敏感性。[19][20]在这些情况下，虽然它往往是最重要的实际特性，但定义中不必说明“对初始条件的敏感性”。


如果注意力被限制在时间间隔内，[21]那么第二个性质就意味着另外两个性质。混沌的另一种定义和一般较弱的定义只使用了上面列表中的前两个属性。 [22]


混沌作为拓扑超对称性的自发分解 Chaos as a spontaneous breakdown of topological supersymmetry

在连续时间动力系统中，混沌是拓扑超对称性的自发破坏现象，是所有随机和确定性(偏)微分方程的发展算子的内在属性。[23][24]这种动态混沌图像不仅适用于确定性模型，也适用于有外部噪声的模型。外部噪声是物理学上的一个重要概括，因为在现实中，所有的动态系统都受到其随机环境的影响。在这幅图中，与混沌动力学相关的远程动力学行为(例如，蝴蝶效应)是戈德斯通定理的结果——在自发的拓扑超对称破坏中的应用。


对初始条件的敏感性 Sensitivity to initial conditions

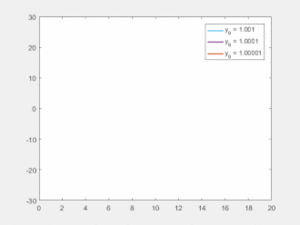
用于绘制 y 变量图的洛伦兹方程。 x 和 z的初始条件保持不变，y 的初始条件在1.001、1.0001和1.00001之间变化。[math]\displaystyle{ \rho }[/math], [math]\displaystyle{ \sigma }[/math] 和[math]\displaystyle{ \beta }[/math] 分别为 45.92, 16 和 4 。从图表中可以看出，在这三种情况下，即使初始值的最细微差别也会在大约12秒的进化后引起重大变化。这是对初始条件敏感依赖的一个例子。

对初始条件的敏感性意味着一个混沌系统中的每个点都被其他点任意地近似，具有明显不同的未来路径或轨迹。因此，任意小的改变或者对当前轨迹的扰动都可能导致明显不同的未来行为。[3]


对初始条件的敏感性通常被称为“蝴蝶效应” ，这是因为Edward Lorenz在1972年给华盛顿特区的美国美国科学进步协会学会的一篇题为《可预测性: 巴西蝴蝶翅膀的扇动是否会在德克萨斯州引发龙卷风 Predictability: Does the Flap of a Butterfly's Wings in Brazil set off a Tornado in Texas?》的论文。[25] 扑翼代表了系统初始条件的一个小的变化，这导致了一系列的事件，阻止了大规模现象的可预测性。如果蝴蝶没有扇动翅膀，整个系统的轨迹可能会大不相同。


对初始条件敏感的一个后果是，如果我们从有限数量的系统信息开始(在实践中通常是这样) ，然后超过一定的时间，系统将不再是可预测的。这种情况在天气情况下最为普遍，而天气一般只能预测一周之后的情况。[26]这并不意味着人们不能断言任何关于遥远未来的事件——只是对系统存在一些限制。例如，我们确实知道，在当前的地质年代，地球的温度不会自然达到100摄氏度或降至-130摄氏度，但这并不意味着我们能够准确预测一年中哪一天的温度最高。


用更精确的数学术语来说，李亚普诺夫指数 Lyapunov exponent方法测量了对初始条件的敏感度，以指数发散率的形式从扰动的初始条件。[27] 更具体地说，给定相空间中无穷小相近的两个起始轨迹，利用初始分离数学[math]\displaystyle{ \delta \mathbf{Z}_0 }[/math]，这两个轨迹最终以给定的速率发散。


[math]\displaystyle{ | \delta\mathbf{Z}(t) | \approx e^{\lambda t} | \delta \mathbf{Z}_0 |, }[/math]


其中，[math]\displaystyle{ t }[/math]是时间[math]\displaystyle{ \lambda }[/math]是李亚普诺夫指数。分离速率取决于初始分离向量的方向，因此可以存在一个完整的李雅普诺夫指数谱。李雅普诺夫指数的个数等于相空间的维数，尽管通常只是指最大的维数。例如，最大李亚普诺夫指数(MLE) 是最常用的，因为它决定了系统的整体可预测性。正极大似然估计通常被认为是系统混沌的表现。[6]


除了上述性质外，还存在与初始条件敏感性有关的其他性质。这些包括，例如，测量理论混合(如遍历理论 Kolmogorov automorphism中所讨论的)和K系统 K-system的性质。[9]


非周期性 Non-periodicity

一个混沌系统可能具有演化变量的值序列，这些值精确地重复自己，从序列中的任何一点开始给出周期性行为。然而，这样的周期序列是排斥而不是吸引，这意味着如果演化变量在序列之外，无论多么接近，它都不会进入序列，事实上将偏离序列。因此，对于几乎所有的初始条件，变量的演化是混沌的，具有非周期性的行为。


拓扑混合 Topological mixing

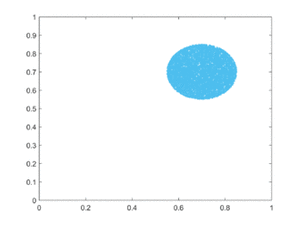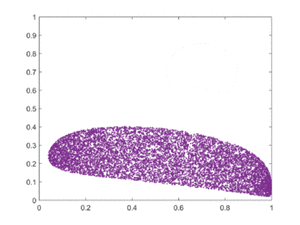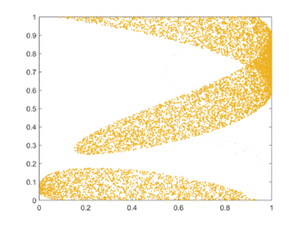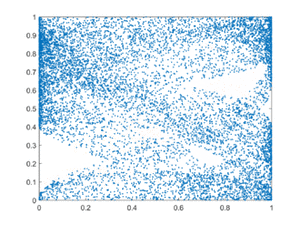
一组状态数学[math]\displaystyle{ [x,y] }[/math]的六次迭代通过 logistic 映射。第一个迭代(蓝色)是初始条件，它基本上形成一个圆。动画显示了循环初始条件的第一次到第六次迭代。可以看出，混合发生在我们迭代的过程中。第六次迭代结果表明，这些点在相空间中几乎完全分散。如果我们在迭代中取得进一步的进展，混合将是均匀的和不可逆的。Logistic 映射有方程式 [math]\displaystyle{ x_{k+1} = 4 x_k (1 - x_k ) }[/math]。为了将逻辑映射的状态空间扩展为二维，将第二种状态[math]\displaystyle{ y }[/math]被创建为 [math]\displaystyle{ y_{k+1} = x_k + y_k }[/math]，如果 [math]\displaystyle{ x_k + y_k \lt 1 }[/math]和 [math]\displaystyle{ y_{k+1} = x_k + y_k -1 }[/math] 不是这样的。
由x → 4 x (1 – x)和y → (x + y) mod 1 定义的映射还显示拓扑混合。在这里，蓝色区域通过动力学首先转换为紫色区域，然后转换为粉红色和红色区域，最后转换为散布在整个空间中的垂直线条云。 .

拓扑混合(或较弱的拓扑传递性条件)是指系统随着时间的推移不断演化，使其相空间的任何给定区域或开集最终与任何其他给定区域重叠。这种“混合”的数学概念符合标准的直觉，有色染料或液体的混合就是混沌系统的一个例子。


常见的混沌理论忽略了拓扑混合，认为混沌只是对初始条件敏感。然而，对初始条件的敏感依赖本身并不会造成混乱。例如，考虑一下通过反复将初始值加倍而产生的简单的动力系统。这个系统对任何地方的初始条件都有敏感的依赖关系，因为任何一对邻近的点最终都会变得广泛分离。然而，这个例子没有拓扑混合，因此没有混沌。事实上，它的行为极其简单: 除了0以外的所有点都趋向于正或负无穷。


拓扑传递性 Topological transitivity

如果对于[math]\displaystyle{ f:X \to X }[/math]中的任意一对开集数学[math]\displaystyle{ U, V \in X }[/math]，存在数学 [math]\displaystyle{ k \gt 0 }[/math]，则称[math]\displaystyle{ f^{k}(U) \cap V \neq \emptyset }[/math]是拓扑可传递的。拓扑传递性是拓扑混合的一个较弱的形式。直观上，如果一个地图是拓扑传递的，那么给定一个点 x 和一个区域 V，在x附近存在一个点y，这个点的轨道经过 V。 这意味着不可能将系统分解为两个开集。[28]


一个重要的相关定理是Birkhoff 传递性定理 Birkhoff Transitivity Theorem。在拓扑传递性中，稠密轨道的存在是显而易见的。Birkhoff 传递性定理指出，如果X是第二个可数的完备空间，那么拓扑传递性就意味着X中存在一个具有稠密轨道的稠密点集。[29]


周期轨道密度 Density of periodic orbits

对于一个具有稠密周期轨道的混沌系统，意味着空间中的每一点都可以被周期轨道任意逼近。[28]


Sharkovskii 的定理是 Li 和 Yorke [30] (1975)证明的基础，证明了任何一维的连续系统，只要表现出周期为三的规则周期，也会表现出其他长度的规则周期，以及完全混沌的轨道。


奇异吸引子 Strange attractors

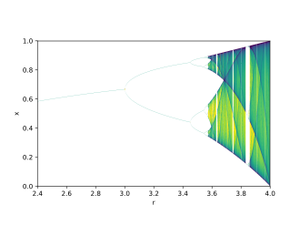
Lorenz吸引子表现出混沌行为。这两个图表明敏感的依赖于初始条件在区域的相空间所占据的吸引子。

一些动力学系统，如一维 logistic 映射所定义的跨度类型x → 4 x (1 – x),，到处都是混沌，但在许多情况下混沌行为只存在于相空间的一个子集中。最令人感兴趣的情况是当混沌行为发生在一个吸引子上时，从那时起一大组初始条件导致轨道收敛到这个混沌区域。[31]


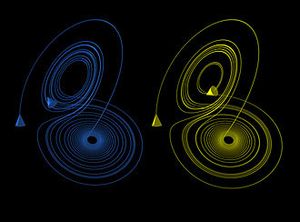
可视化混沌吸引子的一个简单方法是从吸引子的吸引盆中的一个点开始，然后简单地绘制它的后续轨道。由于拓扑传递性条件，这很可能产生整个最终吸引子的图像，而事实上右图所示的两个轨道都给出了Lorenz吸引子的一般形状。这个吸引子来自于洛伦兹天气系统的一个简单的三维模型。Lorenz吸引子也许是最著名的混沌系统图之一，可能是因为它不仅是最早的一个，而且也是最复杂的一个，因此产生了一个非常有趣的图案，稍加想象，看起来就像一只蝴蝶的翅膀。


与定点吸引子和极限环不同，混沌系统产生的吸引子，即所谓的奇异吸引子，具有很大的细节和复杂性。奇异吸引子存在于连续动力系统(如 Lorenz 系统)和一些离散系统(如 Hénon 映射)中。其他的离散动力系统有一种叫做 Julia 集的排斥结构，这种结构形成于固定点吸引盆地的边界。 Julia 集可以被认为是奇异的排斥者。奇异吸引子和 Julia 集都具有典型的分形结构，可以计算出它们的分形维数。


混沌系统的最小复杂度 Minimum complexity of a chaotic system

分叉图的的逻辑映射x → r x (1 – x).每个垂直切片显示一个特定值 r的吸引子。 该图显示了随着 r的增加周期翻倍，最终产生混沌。

离散混沌系统，如 logistic 映射，无论其维数如何，都可以表现出奇怪的吸引子。具有抛物线最大值和费根鲍姆常数 Feigenbaum constants[math]\displaystyle{ \delta=4.664201... }[/math],[math]\displaystyle{ \alpha=2.502907... }[/math] [32][33]的一维映射的普适性是显而易见的,将映射作为离散激光动力学的玩具模型提出::[math]\displaystyle{ x \rightarrow G x (1 - \mathrm{tanh} (x)) }[/math],其中，[math]\displaystyle{ x }[/math]代表电场幅度 [math]\displaystyle{ G }[/math] [34]为激光增益分岔参数。[math]\displaystyle{ G }[/math]在区间[math]\displaystyle{ [0, \infty) }[/math]的逐渐增加使动力学从正规变成了混沌，[34][35]，其定性分支图与逻辑图相同。


相比之下，对于连续动力系统，庞加莱-本迪克森定理 Poincaré–Bendixson theorem表明奇异吸引子只能出现在三维或三维以上。有限维线性系统永远不会是混沌的; 一个动力系统要表现出混沌行为，它必须是非线性的或无限维的。


庞加莱-本迪克森定理指出，二维微分方程具有非常规则的行为。下面讨论的Lorenz吸引子是由三个微分方程组组成的，例如:

[math]\displaystyle{ \begin{align} \frac{\mathrm{d}x}{\mathrm{d}t} &= \sigma y - \sigma x, \\ \frac{\mathrm{d}y}{\mathrm{d}t} &= \rho x - x z - y, \\ \frac{\mathrm{d}z}{\mathrm{d}t} &= x y - \beta z. \end{align} }[/math]


[math]\displaystyle{ x }[/math]，[math]\displaystyle{ y }[/math]，[math]\displaystyle{ z }[/math]组成系统状态，[math]\displaystyle{ t }[/math]是时间，[math]\displaystyle{ \sigma }[/math]，[math]\displaystyle{ \rho }[/math]，[math]\displaystyle{ \beta }[/math]是系统参数。右边的五项是线性项，两项是二次项，总共有七项。另一个著名的混沌吸引子是由 r ssler 方程产生的，它只有七个非线性项中的一个。斯普洛特 Sprott[36]发现了一个只有五个项的三维系统，其中只有一个非线性项，对于某些参数值呈现混沌。张和Heidel[37][38] 表明，至少对于耗散和保守的二次系统，右边只有三个或四个项的三维二次系统不能表现出混沌行为。原因很简单，这类系统的解是渐近于二维表面的，因此解的行为是良好的。


虽然庞加莱-本迪克森定理表明欧氏平面上的连续动力系统不可能是混沌的，但具有非欧几里得几何的二维连续系统可以表现出混沌行为。[39]也许令人惊讶的是，混沌也可能发生在线性系统中，只要它们是无限维的。[40] 线性混沌理论正在数学分析的一个分支——泛函分析中得到发展


无限维地图 Infinite dimensional maps

耦合离散映射的直接推广[41]基于卷积积分，它调节空间分布映射之间的相互作用:


[math]\displaystyle{ \psi_{n+1}(\vec r,t) = \int K(\vec r - \vec r^{,},t) f [\psi_{n}(\vec r^{,},t) ]d {\vec r}^{,} }[/math],


其中，核心[math]\displaystyle{ K(\vec r - \vec r^{,},t) }[/math]是作为相关物理系统的格林函数导出的传播子，[42] 。[math]\displaystyle{ f [\psi_{n}(\vec r,t) ] }[/math] 可能是逻辑映射，类似于 [math]\displaystyle{ \psi \rightarrow G \psi [1 - \tanh (\psi)] }[/math]或复合映射，例如Julia 集合 [math]\displaystyle{ f[\psi] = \psi^2 }[/math]或Ikeda映射[math]\displaystyle{ \psi_{n+1} = A + B \psi_n e^{i (|\psi_n|^2 + C)} }[/math] 当波的传播距离 [math]\displaystyle{ L=ct }[/math]和波长[math]\displaystyle{ \lambda=2\pi/k }[/math]认为是核[math]\displaystyle{ K }[/math] 可以具有用于格林函数的形式薛定谔方程：[43].[44]


[math]\displaystyle{ K(\vec r - \vec r^{,},L) = \frac {ik\exp[ikL]}{2\pi L}\exp[\frac {ik|\vec r-\vec r^{,}|^2}{2 L} ] }[/math].


挺举系统 Jerk systems

在物理学中，挺度是位置对时间的三阶导数。这样，微分方程的形式:


[math]\displaystyle{ J\left(\overset{...}{x},\ddot{x},\dot {x},x\right)=0 }[/math]


有时被称为 Jerk 等式。证明了 jerk 方程等价于三个一阶非线性常微分方程组，在某种意义上是表现混沌行为的解的最小设定。这激发了人们对挺举系统的数学兴趣。含有四阶或更高阶导数的系统称为相应的超挺举系统。[45]


挺举系统的行为用挺举方程描述，对于某些挺举方程，简单的电子线路可以建立解的模型。这些回路被称为挺举回路。


挺举电路最有趣的性质之一是混沌行为的可能性。实际上，某些著名的混沌系统，如 Lorenz吸引子和 r-ssler 映射，通常被描述为三个一阶微分方程组成的系统，它们可以组合成一个单一的(虽然相当复杂) jerk 方程。非线性 jerk 系统在某种意义上是表现出混沌行为的最小复杂系统，不存在只包含两个一阶常微分方程的混沌系统(只产生一个二阶方程的系统)。


一个在[math]\displaystyle{ x }[/math]数量级中带有非线性的 jerk 方程的例子是:


[math]\displaystyle{ \frac{\mathrm{d}^3 x}{\mathrm{d} t^3}+A\frac{\mathrm{d}^2 x}{\mathrm{d} t^2}+\frac{\mathrm{d} x}{\mathrm{d} t}-|x|+1=0. }[/math]


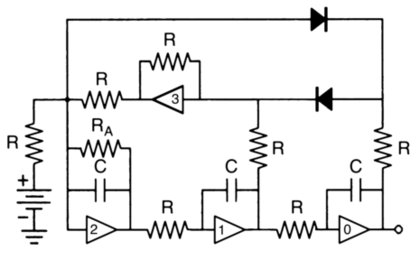
这里，A是一个可调参数。该方程对A=3/5有一个混沌解，可以用下面的冲击电路实现，所需的非线性是由两个二极管带来的:


JerkCircuit01.png

在上述电路中，除[math]\displaystyle{ R_A=R/A=5R/3 }[/math]外，所有电阻值相等，所有电容值相等。主频是 [math]\displaystyle{ 1/2\pi R C }[/math]。运算放大器0的输出对应于 x 变量，1的输出对应于 x 的一阶导数，2的输出对应于二阶导数。


类似的电路只需要一个二极管[46]或根本不需要二极管。[47]


又见著名的蔡氏电路，混沌真随机数发生器的基础之一。[48]电路结构的简易性使它成为一个无处不在的现实世界中的混沌系统的例子。

自发秩序 Spontaneous order

在适当的条件下，混沌自然而然地演化成一种步调一致的模式。在Kuramoto模型中，四个条件足以产生混沌系统的同步。例子包括克里斯蒂安·惠更斯 Christiaan Huygens钟摆的耦合振荡、萤火虫、神经元、伦敦千禧桥共振以及大型约瑟夫森结阵列 Josephson junctions。[49]


历史

巴恩斯利蕨类植物是用混沌游戏创造出来的。可以通过迭代函数系统（IFS）重建自然形式（蕨类植物，云朵，山脉等）。

亨利·庞加莱 Henri Poincaré是混沌理论的早期支持者。19世纪80年代，在研究三体时，他发现有些轨道是非周期性的，但不会永远增加，也不会接近一个固定点。[50][51][52]1898年，雅克·哈达马德 Jacques Hadamard发表了一篇影响深远的论文，研究自由粒子在恒负曲率表面上无摩擦滑行的混沌运动，这篇论文被称为“ Hadamard 台球”。[53]Hadamard能够证明所有的轨道都是不稳定的，所有的粒子轨道都以指数形式彼此分离，李亚普诺夫指数为正。


混沌理论起源于遍历理论。后来的研究，也是关于非线性微分方程的主题，由乔治·戴维·伯克霍夫 George David Birkhoff，[54]安德雷·柯尔莫哥洛夫 Andrey Nikolaevich Kolmogorov，[55][56][57]玛丽·露西·卡特赖特 Mary Lucy Cartwright 和约翰·恩瑟·李特尔伍德 John Edensor Littlewood，[58]和斯蒂芬·斯梅尔 Stephen Smale进行。[59]除了Smale，这些研究都直接受到物理学的启发: Birkhoff的三体，Kolmogorov 的湍流和天文学问题，Cartwright和Littlewood的无线电工程。虽然还没有观察到混沌的行星运动，但实验人员已经遇到了流体运动中的湍流和无线电电路中的非周期性振荡，而没有一个理论来解释他们所看到的。


尽管在20世纪上半叶有了初步的认识，但混沌理论直到本世纪中叶才正式形成，当时一些科学家首次发现，线性理论，当时流行的系统理论，根本无法解释某些实验的观察行为，比如logistic映射。混沌理论家认为测量不精确和简单的“噪声”是所研究系统的完整组成部分。


电子计算机是混沌理论发展的主要催化剂。许多混沌理论的数学涉及简单数学公式的重复迭代，手工操作是不切实际的。电子计算机使这些重复的计算变得可行，而图形和图像使这些系统可视化成为可能。1961年11月27日，作为林千寻在京都大学实验室的研究生，Yoshisuke Ueda 正在用模拟计算机进行实验，他注意到了他所说的“随机过渡现象”。然而他的顾问当时并不同意他的结论，并且直到1970年才允许他报告他的发现。[60][61]


来自飞机机翼的尖涡中的湍流。研究系统产生湍流的临界点对混沌理论很重要，例如苏联物理学家 Lev Landau 分析了这个临界点，他发展了湍流的 Landau-hopf 理论。后来 David Ruelle 和 Floris Takens 针对 Landau 预测，湍流可以通过一个奇异吸引子发展，这是混沌理论的一个主要概念


爱德华·洛伦茨 Edward Lorenz是这一理论的早期开拓者。他对混沌的兴趣来源于1961年他在天气预报方面的工作。[11]Lorenz正在使用一台简单的数字计算机，一台 Royal McBee LGP-30运行他的天气模拟。他想再看一次数据序列，为了节省时间，他在模拟过程中间开始了模拟。他通过输入一个打印输出的数据，这些数据对应于原始模拟中的条件。令他惊讶的是，机器开始预测的天气与以前的计算完全不同。Lorenz通过计算机打印出来的资料查到了这一点。计算机以6位数的精度工作，但打印输出的变量四舍五入到一个3位数字，所以像0.506127这样的值打印为0.506。这种差异是微小的，当时的共识是它不应该有任何实际效果。然而，Lorenz发现，初始条件的微小变化会导致长期结果的巨大变化。[62]Lorenz的发现，这给它的名字洛伦茨吸引子，表明即使详细的大气模型，一般来说，不能作出精确的长期天气预报。


1963年，伯努·瓦·曼德布洛特 Benoit Mandelbrot在棉花价格数据中发现了各种规模的循环模式。[63]事先他研究过信息理论，并得出结论，噪音的模式类似于康托集: 在任何尺度上，包含噪音的周期与无误差的周期的比例是一个常数——因此误差是不可避免的，必须通过引入冗余来计划。[64]Mandelbrot既描述了“诺亚效应”(可能会发生突然的不连续变化) ，也描述了“约瑟夫效应 Joseph effect”(可能会持续一段时间，然后突然改变)。[65][66]这挑战了价格变化是正态分布的观点。1967年，他出版了《英国的海岸线有多长？统计自相似性和分维数”，显示海岸线的长度随测量仪器的规模而变化，在所有规模上都与仪器相似，而且对于一个极小的测量装置来说，长度是无限的。[67]他认为，从远处(0维)看，一个线球似乎是一个点，从相当接近(3维)看，一个球，或一个曲线(一维) ，他认为，一个物体的尺寸是相对于观察者，可能是分数。如果一个物体的不规则性在不同尺度上是常数(“自相似”) ，那么这个物体就是一个分形(例如门格尔海绵 the Menger sponge、赛尔皮滑雪垫圈 the Sierpiński gasket和科氏曲线或雪花 Koch curve or snowflake，它们是无限长的，但覆盖着一个有限的空间，分形维数约为1.2619)。1982年，Mandelbrot发表了《自然的分形几何》 ，成为混沌理论的经典之作。[68]生物学系统，如循环系统和支气管系统的分支证明符合一个分形模型。[69]


1977年12月，纽约科学院组织了第一次关于混沌的研讨会，出席的有大卫·鲁尔 David Ruelle、罗伯特·梅 Robert May、詹姆斯·a·约克 James A. Yorke(数学中“混沌”一词的创始人)、罗伯特·肖 Robert Shaw和气象学家爱德华·洛伦茨 Edward Lorenz。第二年 Pierre Coullet 和 Charles Tresser 发表了《迭代与重整化群体 Iterations d'endomorphismes et groupe de renormalisation》 ，米切尔·费根鲍姆 Mitchell Feigenbaum的文章《一类非线性变换的定量普遍性 Quantitative Universality for a Class of Nonlinear Transformations》最终发表在一本杂志上，经过三年的裁判拒绝。[33][70] 因此 Feigenbaum (1975)和 Coullet & Tresser (1978)发现了混沌中的普遍性，允许混沌理论应用于许多不同的现象。


1979年，Albert j. Libchaber 在皮埃尔·奥昂贝格 Pierre Hohenberg在阿斯彭组织的一次研讨会上，提出了他对瑞利-贝纳德对流系统 Rayleigh–Bénard convection中导致混沌和湍流的分叉理论级联的实验观察。1986年，由于他们令人鼓舞的成就，他和Mitchell Feigenbaum一起被授予沃尔夫物理学奖。


1986年，纽约科学院与国家心理健康研究所和海军研究办公室共同组织了第一次关于生物学和医学中的混沌的重要会议。在那里，贝尔纳多·休伯曼 Bernardo Huberman提出了一个精神分裂症患者眼球追踪障碍的数学模型。[71]这导致了生理学的更新在20世纪80年代通过应用混沌理论，例如，在病理心脏周期的研究。


1987年，Per Bak，Chao Tang 和 Kurt Wiesenfeld 在《物理评论快报 Physical Review Letters》上发表了一篇论文，[72]首次描述了自组织临界性，认为自然界复杂性产生的机制之一。


除了大量基于实验室的方法，如 Bak-Tang-Wiesenfeld 沙堆法 Bak–Tang–Wiesenfeld sandpile，许多其他的研究都集中在大规模的自然或社会系统上，这些系统已知(或怀疑)表现出尺度不变的行为。虽然这些方法并不总是受到研究对象专家的欢迎(至少最初是这样) ，但 SOC 已经成为解释一些自然现象的有力候选者，包括地震(早在 SOC 被发现之前，它就被认为是尺度不变行为的来源，例如描述地震大小统计分布的古腾堡-里克特定律 Gutenberg–Richter law，描述余震频率的 Omori 定律) ，[73] 太阳，经济系统的波动，例如金融市场(SOC 在经济物理学中很常见) ，地貌形成，森林火灾，流行病和生物进化 (在 SOC 被调用的地方，例如 Niles Eldredge 和史蒂芬·古尔德 Stephen Jay Gould提出的“间断平衡”理论背后的动力机制)。考虑到事件规模无标度分布的含义，一些研究人员提出，另一个应该被视为 SOC 的例子的现象是战争的发生。对土壤有机碳的这些研究既包括建立模型的尝试(开发新模型或使现有模型适应特定自然系统的具体情况) ，也包括广泛的数据分析，以确定自然定标法的存在和 / 或特点。


同年，詹姆斯•格莱克 James Gleick出版了《混沌: 创造新科学 Chaos: Making a New Science》一书，成为畅销书，并向广大公众介绍了混沌理论的一般原理及其历史，但他对苏联的重要贡献重视不够。[74] 混沌理论最初只是少数孤立个体的领域，逐渐成为一门跨学科和制度学科，主要以非线性系统分析的名义出现。许多“混沌论者”(正如一些人自己描述的那样)提到了 Thomas Kuhn 在《科学革命的结构 The Structure of Scientific Revolutions》(1962)提出的范式转换的概念，声称这个新理论就是这种转换的一个例子，这是 Gleick 支持的一个论点。


更便宜、更强大的计算机的出现拓宽了混沌理论的适用性。目前，混沌理论仍然是一个活跃的研究领域，[75]涉及许多不同的学科(数学、拓扑学、物理学、[76]社会系统、[77]人口模型、生物学、气象学、天体物理学、信息理论、计算神经科学等等)。).

应用

一个圆锥形纺织外壳，外观与第30条规则相似，一个行为混乱的细胞自动机[78]

虽然混沌理论诞生于观测天气模式，但它已经适用于各种其他情况。今天受益于混沌理论的领域包括地质学、数学、微生物学、生物学、计算机科学、经济学、[79][80][81]工程学、[82][83]金融学、[84][85]算法贸易、[86][87][88]气象学、哲学、人类学、[89] 政治学、[90][91][92]族群动态、[93] 心理学[94]和机器人学。下面列出了一些类别和示例，但这绝不是一个全面的清单，因为新的应用程序正在出现。


密码学

混沌理论在密码学中已应用多年。在过去的几十年中，混沌和非线性动力学被用于数百种密码原语的设计。这些算法包括图像加密算法，散列函数，安全伪随机数生成器，流密码，水印和隐写术。[95] 这些算法大多基于单模态混沌映射，其中很大一部分以控制参数和混沌映射的初始条件为关键。[96]从更广泛的角度来看，混沌映射和密码系统之间的相似性是设计基于混沌的密码算法的主要不失一般性。[97]另一种类型的计算，DNA 计算，与混沌理论相结合，提供了一种加密图像和其他信息的方法。[98] 许多DNA-混沌密码算法被证明是不安全的，或者应用的技术是不高效的。[99][100][101]


机器人学

机器人学是最近受益于混沌理论的另一个领域。混沌理论已经被用来建立一个预测模型，而不是机器人通过反复试验来改进与环境的相互作用。[102]被动行走的两足机器人展示了混沌动力学。[103]


生物学

一百多年来，生物学家一直在用种群模型跟踪不同物种的种群。大多数模型是连续的，但是最近科学家已经能够在某些种群中实现混沌模型。[104]例如，一项关于加拿大猞猁模型的研究表明，其种群增长存在混乱行为。[105]混乱也可以发现在生态系统，如水文学。虽然水文学的混沌模型有其自身的缺点，但是从混沌理论的角度来看数据还有很多值得学习的地方。[106] 另一个生物学应用是发现在心血管造影术。胎儿监护是在尽可能无创的情况下获得准确信息的人海万花筒(电影)。通过混沌建模可以获得较好的胎儿缺氧预警信号模型。[107]


其他范畴

在化学方面，预测气体的溶解度对于聚合物的制造是至关重要的，但是使用微粒群算法(PSO)的模型往往会收敛到错误的粒子群优化。通过引入混沌，改进了粒子群优化算法，避免了仿真陷入僵局。[108]在21天体力学，特别是在观测小行星时，应用混沌理论可以更好地预测这些天体何时会接近地球和其他行星。[109]冥王星的五个卫星中有四个以混乱的方式旋转。在量子物理和电子工程中，混沌理论对约瑟夫森结大阵列的研究有很大的帮助。[110]离家更近的地方，煤矿一直是危险的地方，频繁的天然气泄漏导致许多人死亡。直到最近，还没有可靠的方法来预测它们何时会发生。但是这些天然气泄漏有混乱的趋势，如果正确地建模，可以相当准确地预测。[111]


混沌理论可以应用于自然科学之外的领域，但是从历史上看，几乎所有这类研究都存在缺乏可重复性、外部效度不足和 / 或对交叉验证缺乏关注等问题，从而导致预测准确性差(如果尝试过样本外预测)。格拉斯 Glass[112]、曼德尔 Mandell和塞尔兹Selz [113]发现，迄今为止，没有任何脑电图研究表明存在奇怪吸引子或其他混沌行为的迹象。


研究人员继续将混沌理论应用于心理学。例如，在模拟群体行为中，异质成员可能表现为不同程度的共享，威尔弗雷德·比昂 Wilfred Bion的理论是一个基本假设，研究人员发现，群体动态是成员个人动态的结果: 每个个人在不同的尺度上再现群体动态，群体的混沌行为反映在每个成员。[114]


雷丁顿 Redington和 Reidbord (1992)试图证明人类的心脏可以表现出混乱的特征。他们监测了一位心理治疗患者在治疗过程中经历不同情绪强度时的心跳间隔时间的变化。结果无可否认是不确定的。不仅在作者制作的各种图表中存在模糊性，据称显示了混沌动力学的证据(频谱分析、相轨迹和自相关图) ，而且当他们试图计算李亚普诺夫指数作为更确定的混沌行为的确认时，作者发现他们不能可靠地这样做。[115]


在他们1995年的论文中，梅特卡夫 Metcalf和艾伦 Allen[116]坚持认为他们在动物行为中发现了一种周期加倍导致混乱的模式。作者们研究了一种众所周知的反应，称为时间表诱发的多饮，通过这种方法，一只动物在一定时间内缺乏食物，当食物最终呈现时，它会喝下不寻常数量的水。这里的控制参数(r)是恢复喂食间隔的长度。作者小心翼翼地测试了大量的动物并进行了许多复制实验，他们设计实验的目的是为了排除反应模式的改变是由不同的起始位置引起的可能性。


时间序列和第一延迟图为所提出的要求提供了最好的支持，随着喂食时间的增加，从周期性到不规则性的发展变化相当明显。另一方面，各种相轨迹图和谱分析与其他图形或整体理论不匹配，不可避免地导致混沌诊断。例如，相轨迹并没有显示一个朝着越来越复杂的方向发展的确切过程(并且远离周期性) ; 这个过程看起来相当混乱。此外，梅特卡夫和艾伦在他们的光谱图中看到了两个和六个周期，这里也有其他解释的空间。所有这些模糊性都需要一些曲折的、事后的解释，以表明结果符合混沌模型。


红色的车和蓝色的车轮流行驶，红色的只向上行驶，蓝色的向右行驶。每一次，如果前面没有车，所有颜色相同的车都试图移动一步。在这里，模型有自我组织在一个有点几何图形模式，其中有一些交通堵塞和一些地区的汽车可以移动在最高速度。

通过调整职业咨询的模型，包括对雇员和就业市场之间关系的混乱解释，安尼森和布莱特发现，对于那些在职业决策中挣扎的人们，可以提出更好的建议。[117]现代组织越来越多地被视为具有基本的自然非线性结构的开放复杂适应系统，受到可能导致混乱的内部和外部力量的影响。例如，团队建设和团队发展作为一个内在的不可预测的系统正在越来越多地被研究，因为不同的个体第一次见面的不确定性使得团队的轨迹不可知。[118]


有人说混沌隐喻是以数学模型和人类行为的心理方面为基础的语言理论，为描述小型工作组的复杂性提供了有益的见解，超越了比喻本身。[119]


通过混沌理论的应用也可以改进经济模型，但是预测一个经济系统的健康状况以及什么因素对其影响最大是一个极其复杂的任务。[120]经济和金融系统与古典自然科学中的系统有着根本的不同，因为前者本质上是随机的，因为它们来自于人们之间的相互作用，因此纯粹的确定性模型不可能提供准确的数据表示。检验经济学和金融学中混沌的实证文献呈现出非常复杂的结果，部分原因是混沌的具体检验与非线性关系的更一般检验之间的混淆。[121]


应用混沌理论进行交通量预测具有重要意义。更好地预测交通将在何时发生将允许采取措施在它发生之前驱散它。将混沌理论原理与其他一些方法相结合，得到了一个更精确的短期预测模型(见右边 BML 流量模型的图)。[122]


混沌理论已经应用于环境水循环数据(又称水文数据) ，如降雨和径流。[123]这些研究产生了有争议的结果，因为检测混沌特征的方法往往是相对主观的。早期的研究倾向于“成功地”发现混沌，而后来的研究和元分析则对这些研究提出质疑，并解释了为什么这些数据集不可能具有低维混沌动力学。[124]

参见

混沌系统的例子

其他相关话题

相关人物

参考文献

  1. ↑ "The Definitive Glossary of Higher Mathematical Jargon — Chaos". Math Vault (in English). 2019-08-01. Retrieved 2019-11-24.{{cite web}}: CS1 maint: url-status (link)
  2. ↑ "chaos theory | Definition & Facts". Encyclopedia Britannica (in English). Retrieved 2019-11-24.
  3. ↑ 3.0 3.1 "What is Chaos Theory? – Fractal Foundation" (in English). Retrieved 2019-11-24.
  4. ↑ Weisstein, Eric W. "Chaos". mathworld.wolfram.com (in English). Retrieved 2019-11-24.
  5. ↑ Kellert, Stephen H. (1993). In the Wake of Chaos: Unpredictable Order in Dynamical Systems. University of Chicago Press. p. 32. ISBN 978-0-226-42976-2. https://archive.org/details/inwakeofchaosunp0000kell. 
  6. ↑ 6.0 6.1 6.2 Bishop, Robert (2017), "Chaos", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Spring 2017 ed.), Metaphysics Research Lab, Stanford University, retrieved 2019-11-24
  7. ↑ Kellert, Stephen H. (1993). In the Wake of Chaos: Unpredictable Order in Dynamical Systems. University of Chicago Press. p. 56. ISBN 978-0-226-42976-2. https://archive.org/details/inwakeofchaosunp0000kell. 
  8. ↑ Kellert, Stephen H. (1993). In the Wake of Chaos: Unpredictable Order in Dynamical Systems. University of Chicago Press. p. 62. ISBN 978-0-226-42976-2. https://archive.org/details/inwakeofchaosunp0000kell. 
  9. ↑ 9.0 9.1 Werndl, Charlotte (2009). "What are the New Implications of Chaos for Unpredictability?". The British Journal for the Philosophy of Science. 60 (1): 195–220. arXiv:1310.1576. doi:10.1093/bjps/axn053.
  10. ↑ Danforth, Christopher M. (April 2013). "Chaos in an Atmosphere Hanging on a Wall". Mathematics of Planet Earth 2013. Retrieved 12 June 2018.
  11. ↑ 11.0 11.1 Lorenz, Edward N. (1963). "Deterministic non-periodic flow". Journal of the Atmospheric Sciences. 20 (2): 130–141. Bibcode:1963JAtS...20..130L. doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2.
  12. ↑ Ivancevic, Vladimir G.; Tijana T. Ivancevic (2008). Complex nonlinearity: chaos, phase transitions, topology change, and path integrals. Springer. ISBN 978-3-540-79356-4. 
  13. ↑ Hubler, A (1989). "Adaptive control of chaotic systems". Swiss Physical Society. Helvetica Physica Acta 62: 339–342.
  14. ↑ Wisdom, Jack; Sussman, Gerald Jay (1992-07-03). "Chaotic Evolution of the Solar System". Science (in English). 257 (5066): 56–62. Bibcode:1992Sci...257...56S. doi:10.1126/science.257.5066.56. hdl:1721.1/5961. ISSN 1095-9203. PMID 17800710.
  15. ↑ Sync: The Emerging Science of Spontaneous Order, Steven Strogatz, Hyperion, New York, 2003, pages 189–190.
  16. ↑ Definition of chaos at Wiktionary;
  17. ↑ "Definition of chaos | Dictionary.com". www.dictionary.com (in English). Retrieved 2019-11-24.
  18. ↑ Hasselblatt, Boris; Anatole Katok (2003). A First Course in Dynamics: With a Panorama of Recent Developments. Cambridge University Press. ISBN 978-0-521-58750-1. 
  19. ↑ Elaydi, Saber N. (1999). Discrete Chaos. Chapman & Hall/CRC. p. 117. ISBN 978-1-58488-002-8. 
  20. ↑ Basener, William F. (2006). Topology and its applications. Wiley. p. 42. ISBN 978-0-471-68755-9. 
  21. ↑ Vellekoop, Michel; Berglund, Raoul (April 1994). "On Intervals, Transitivity = Chaos". The American Mathematical Monthly. 101 (4): 353–5. doi:10.2307/2975629.
  22. ↑ Medio, Alfredo; Lines, Marji (2001). Nonlinear Dynamics: A Primer. Cambridge University Press. p. 165. ISBN 978-0-521-55874-7. 
  23. ↑ Ovchinnikov, I.V. (March 2016). "Introduction to Supersymmetric Theory of Stochastics". Entropy. 18 (4): 108. arXiv:1511.03393. Bibcode:2016Entrp..18..108O. doi:10.3390/e18040108.
  24. ↑ Ovchinnikov, I.V.; Schwartz, R. N.; Wang, K. L. (2016). "Topological supersymmetry breaking: Definition and stochastic generalization of chaos and the limit of applicability of statistics". Modern Physics Letters B. 30 (8): 1650086. arXiv:1404.4076. Bibcode:2016MPLB...3050086O. doi:10.1142/S021798491650086X.
  25. ↑ "Edward Lorenz, father of chaos theory and butterfly effect, dies at 90". MIT News. Retrieved 2019-11-24.
  26. ↑ Watts, Robert G. (2007). Global Warming and the Future of the Earth. Morgan & Claypool. p. 17. 
  27. ↑ Weisstein, Eric W. "Lyapunov Characteristic Exponent". mathworld.wolfram.com (in English). Retrieved 2019-11-24.
  28. ↑ 28.0 28.1 Devaney, Robert L. (2003). An Introduction to Chaotic Dynamical Systems (2nd ed.). Westview Press. ISBN 978-0-8133-4085-2. https://books.google.com/books?id=CjAnY99LwTgC. 
  29. ↑ Robinson, Clark (1995). Dynamical systems: Stability, symbolic dynamics, and chaos. CRC Press. ISBN 0-8493-8493-1. 
  30. ↑ Li, T.Y.; Yorke, J.A. (1975). "Period Three Implies Chaos" (PDF). American Mathematical Monthly. 82 (10): 985–92. Bibcode:1975AmMM...82..985L. CiteSeerX 10.1.1.329.5038. doi:10.2307/2318254. Archived from the original (PDF) on 2009-12-29.
  31. ↑ Strelioff, Christopher; et., al. (2006). "Medium-Term Prediction of Chaos". Phys. Rev. Lett. 96 (4): 044101. Bibcode:2006PhRvL..96d4101S. doi:10.1103/PhysRevLett.96.044101. PMID 16486826.
  32. ↑ Feigenbaum, M. J. (1976) "Universality in complex discrete dynamics", Los Alamos Theoretical Division Annual Report 1975-1976
  33. ↑ 33.0 33.1 Feigenbaum, Mitchell (July 1978). "Quantitative universality for a class of nonlinear transformations". Journal of Statistical Physics. 19 (1): 25–52. Bibcode:1978JSP....19...25F. CiteSeerX 10.1.1.418.9339. doi:10.1007/BF01020332.
  34. ↑ 34.0 34.1 Okulov, A Yu; Oraevskiĭ, A N (1986). "Space–temporal behavior of a light pulse propagating in a nonlinear nondispersive medium". J. Opt. Soc. Am. B. 3 (5): 741–746. Bibcode:1986OSAJB...3..741O. doi:10.1364/JOSAB.3.000741.
  35. ↑ Okulov, A Yu; Oraevskiĭ, A N (1984). "Regular and stochastic self-modulation in a ring laser with nonlinear element". Soviet Journal of Quantum Electronics. 14 (2): 1235–1237. Bibcode:1984QuEle..14.1235O. doi:10.1070/QE1984v014n09ABEH006171.
  36. ↑ Sprott, J.C. (1997). "Simplest dissipative chaotic flow". Physics Letters A. 228 (4–5): 271–274. Bibcode:1997PhLA..228..271S. doi:10.1016/S0375-9601(97)00088-1.
  37. ↑ Fu, Z.; Heidel, J. (1997). "Non-chaotic behaviour in three-dimensional quadratic systems". Nonlinearity (journal). 10 (5): 1289–1303. Bibcode:1997Nonli..10.1289F. doi:10.1088/0951-7715/10/5/014.
  38. ↑ Heidel, J.; Fu, Z. (1999). "Nonchaotic behaviour in three-dimensional quadratic systems II. The conservative case". Nonlinearity. 12 (3): 617–633. Bibcode:1999Nonli..12..617H. doi:10.1088/0951-7715/12/3/012.
  39. ↑ Rosario, Pedro (2006). Underdetermination of Science: Part I. Lulu.com. ISBN 978-1411693913. [self-published source]
  40. ↑ Bonet, J.; Martínez-Giménez, F.; Peris, A. (2001). "A Banach space which admits no chaotic operator". Bulletin of the London Mathematical Society. 33 (2): 196–8. doi:10.1112/blms/33.2.196.
  41. ↑ Adachihara, H; McLaughlin, D W; Moloney, J V; Newell, A C (1988). "Solitary waves as fixed points of infinite‐dimensional maps for an optical bistable ring cavity: Analysis". Journal of Mathematical Physics. 29 (1): 63. Bibcode:1988JMP....29...63A. doi:10.1063/1.528136.
  42. ↑ Okulov, A Yu; Oraevskiĭ, A N (1988). "Spatiotemporal dynamics of a wave packet in nonlinear medium and discrete maps". In N.G. Basov (in Russian). Proceedings of the Lebedev Physics Institute. 187. Nauka. pp. 202–222. 
  43. ↑ Okulov, A Yu (2000). "Spatial soliton laser: geometry and stability". Optics and Spectroscopy. 89 (1): 145–147. Bibcode:2000OptSp..89..131O. doi:10.1134/BF03356001.
  44. ↑ Okulov, A Yu (2020). "Structured light entities, chaos and nonlocal maps". Chaos,Solitons&Fractals. 133 (4): 109638. doi:10.1016/j.chaos.2020.109638.
  45. ↑ K. E. Chlouverakis and J. C. Sprott, Chaos Solitons & Fractals 28, 739–746 (2005), Chaotic Hyperjerk Systems, http://sprott.physics.wisc.edu/pubs/paper297.htm
  46. ↑ "A New Chaotic Jerk Circuit", J. C. Sprott, IEEE Transactions on Circuits and Systems,2011.
  47. ↑ "Simple Autonomous Chaotic Circuits", J. C. Sprott, IEEE Transactions on Circuits and Systems--II: Express Briefs, 2010.
  48. ↑ "Secure Image Encryption Based On a Chua Chaotic Noise Generator", A. S. Andreatos*, and A. P. Leros, Journal of Engineering Science and Technology Review, 2013.
  49. ↑ Steven Strogatz, Sync: The Emerging Science of Spontaneous Order, Hyperion, 2003.
  50. ↑ Poincaré, Jules Henri (1890). "Sur le problème des trois corps et les équations de la dynamique. Divergence des séries de M. Lindstedt". Acta Mathematica. 13 (1–2): 1–270. doi:10.1007/BF02392506.
  51. ↑ Poincaré, J. Henri (2017). The three-body problem and the equations of dynamics : Poincaré's foundational work on dynamical systems theory. Popp, Bruce D. (Translator). Cham, Switzerland: Springer International Publishing. ISBN 9783319528984. 
  52. ↑ Diacu, Florin; Holmes, Philip (1996). Celestial Encounters: The Origins of Chaos and Stability. Princeton University Press. 
  53. ↑ Hadamard, Jacques (1898). "Les surfaces à courbures opposées et leurs lignes géodesiques". Journal de Mathématiques Pures et Appliquées. 4: 27–73.
  54. ↑ George D. Birkhoff, Dynamical Systems, vol. 9 of the American Mathematical Society Colloquium Publications (Providence, Rhode Island: American Mathematical Society, 1927)
  55. ↑ Kolmogorov, Andrey Nikolaevich (1941). "Local structure of turbulence in an incompressible fluid for very large Reynolds numbers". Doklady Akademii Nauk SSSR. 30 (4): 301–5. Bibcode:1941DoSSR..30..301K. Reprinted in: Kolmogorov, A. N. (1991). "The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers". Proceedings of the Royal Society A. 434 (1890): 9–13. Bibcode:1991RSPSA.434....9K. doi:10.1098/rspa.1991.0075.
  56. ↑ Kolmogorov, A. N. (1941). "On degeneration of isotropic turbulence in an incompressible viscous liquid". Doklady Akademii Nauk SSSR. 31 (6): 538–540. Reprinted in: Kolmogorov, A. N. (1991). "Dissipation of Energy in the Locally Isotropic Turbulence". Proceedings of the Royal Society A. 434 (1890): 15–17. Bibcode:1991RSPSA.434...15K. doi:10.1098/rspa.1991.0076.
  57. ↑ Kolmogorov, A. N. (1954). Preservation of conditionally periodic movements with small change in the Hamiltonian function. Lecture Notes in Physics. 98. pp. 527–530. Bibcode 1979LNP....93...51K. doi:10.1007/BFb0021737. ISBN 978-3-540-09120-2.  See also Kolmogorov–Arnold–Moser theorem
  58. ↑ Cartwright, Mary L.; Littlewood, John E. (1945). "On non-linear differential equations of the second order, I: The equation y" + k(1−y2)y' + y = bλkcos(λt + a), k large". Journal of the London Mathematical Society. 20 (3): 180–9. doi:10.1112/jlms/s1-20.3.180. See also: Van der Pol oscillator
  59. ↑ Smale, Stephen (January 1960). "Morse inequalities for a dynamical system". Bulletin of the American Mathematical Society. 66: 43–49. Bibcode:1994BAMaS..30..205W. doi:10.1090/S0002-9904-1960-10386-2.
  60. ↑ Abraham, Ralph (2000). Abraham, Ralph H.; Ueda, Yoshisuke. eds. The Chaos Avant-Garde: Memoirs of the Early Days of Chaos Theory. World Scientific Series on Nonlinear Science Series A. 39. World Scientific. Bibcode 2000cagm.book.....A. doi:10.1142/4510. ISBN 978-981-238-647-2. https://books.google.com/books?id=0E667XpBq1UC. 
  61. ↑ Sprott, Julien Clinton (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 978-0-19-850840-3. https://books.google.com/books?id=SEDjdjPZ158C. 
  62. ↑ Gleick, James (1987). Chaos: Making a New Science. London: Cardinal. p. 17. ISBN 978-0-434-29554-8. 
  63. ↑ Mandelbrot, Benoît (1963). "The variation of certain speculative prices". Journal of Business. 36 (4): 394–419. doi:10.1086/294632.
  64. ↑ Berger J.M.; Mandelbrot B. (1963). "A new model for error clustering in telephone circuits". IBM Journal of Research and Development. 7 (3): 224–236. doi:10.1147/rd.73.0224.
  65. ↑ Mandelbrot, B. (1977). The Fractal Geometry of Nature. New York: Freeman. p. 248. 
  66. ↑ See also: Mandelbrot, Benoît B.; Hudson, Richard L. (2004). The (Mis)behavior of Markets: A Fractal View of Risk, Ruin, and Reward. New York: Basic Books. p. 201. https://archive.org/details/misbehaviorofmar00beno. 
  67. ↑ Mandelbrot, Benoît (5 May 1967). "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension". Science. 156 (3775): 636–8. Bibcode:1967Sci...156..636M. doi:10.1126/science.156.3775.636. PMID 17837158.
  68. ↑ Mandelbrot, B. (1982). The Fractal Geometry of Nature. New York: Macmillan. ISBN 978-0716711865. https://archive.org/details/fractalgeometryo00beno. 
  69. ↑ Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Peng, C.K.; Stanley, H.E. (1994). "Fractals in Biology and Medicine: From DNA to the Heartbeat". In Bunde, Armin; Havlin, Shlomo. Fractals in Science. Springer. pp. 49–89. ISBN 978-3-540-56220-7. 
  70. ↑ Coullet, Pierre, and Charles Tresser. "Iterations d'endomorphismes et groupe de renormalisation." Le Journal de Physique Colloques 39.C5 (1978): C5-25
  71. ↑ Huberman, B.A. (July 1987). "A Model for Dysfunctions in Smooth Pursuit Eye Movement". Annals of the New York Academy of Sciences. 504 Perspectives in Biological Dynamics and Theoretical Medicine (1): 260–273. Bibcode:1987NYASA.504..260H. doi:10.1111/j.1749-6632.1987.tb48737.x. PMID 3477120.
  72. ↑ Bak, Per; Tang, Chao; Wiesenfeld, Kurt (27 July 1987). "Self-organized criticality: An explanation of the 1/f noise". Physical Review Letters. 59 (4): 381–4. Bibcode:1987PhRvL..59..381B. doi:10.1103/PhysRevLett.59.381. PMID 10035754. However, the conclusions of this article have been subject to dispute. "?". Archived from the original on 2007-12-14.. See especially: Laurson, Lasse; Alava, Mikko J.; Zapperi, Stefano (15 September 2005). "Letter: Power spectra of self-organized critical sand piles". Journal of Statistical Mechanics: Theory and Experiment. 0511. L001.
  73. ↑ Omori, F. (1894). "On the aftershocks of earthquakes". Journal of the College of Science, Imperial University of Tokyo. 7: 111–200.
  74. ↑ Gleick, James (August 26, 2008). Chaos: Making a New Science. Penguin Books. ISBN 978-0143113454. 
  75. ↑ Motter, A. E.; Campbell, D. K. (2013). "Chaos at fifty". Phys. Today. 66 (5): 27–33. arXiv:1306.5777. Bibcode:2013PhT....66e..27M. doi:10.1063/pt.3.1977.
  76. ↑ Hubler, A.; Foster, G.; Phelps, K. (2007). "Managing chaos: Thinking out of the box". Complexity. 12 (3): 10. Bibcode:2007Cmplx..12c..10H. doi:10.1002/cplx.20159.
  77. ↑ Kiel, L., ed. (1996) (in en). Chaos Theory in the Social Sciences: Foundations and Applications. Ann Arbor, MI: University of Michigan Press. doi:10.3998/mpub.14623. ISBN 9780472106387. 
  78. ↑ Stephen Coombes (February 2009). "The Geometry and Pigmentation of Seashells" (PDF). www.maths.nottingham.ac.uk. University of Nottingham. Retrieved 2013-04-10.
  79. ↑ Kyrtsou C.; Labys W. (2006). "Evidence for chaotic dependence between US inflation and commodity prices". Journal of Macroeconomics. 28 (1): 256–266. doi:10.1016/j.jmacro.2005.10.019.
  80. ↑ Kyrtsou C., Labys W.; Labys (2007). "Detecting positive feedback in multivariate time series: the case of metal prices and US inflation". Physica A. 377 (1): 227–229. Bibcode:2007PhyA..377..227K. doi:10.1016/j.physa.2006.11.002.
  81. ↑ Kyrtsou, C.; Vorlow, C. (2005). "Complex dynamics in macroeconomics: A novel approach". New Trends in Macroeconomics. Springer Verlag. 
  82. ↑ Hernández-Acosta, M. A.; Trejo-Valdez, M.; Castro-Chacón, J. H.; Miguel, C. R. Torres-San; Martínez-Gutiérrez, H. (2018). "Chaotic signatures of photoconductive Cu 2 ZnSnS 4 nanostructures explored by Lorenz attractors". New Journal of Physics (in English). 20 (2): 023048. Bibcode:2018NJPh...20b3048H. doi:10.1088/1367-2630/aaad41. ISSN 1367-2630.
  83. ↑ Applying Chaos Theory to Embedded Applications
  84. ↑ Hristu-Varsakelis, D.; Kyrtsou, C. (2008). "Evidence for nonlinear asymmetric causality in US inflation, metal and stock returns". Discrete Dynamics in Nature and Society. 2008: 1–7. doi:10.1155/2008/138547. 138547.
  85. ↑ Kyrtsou, C.; M. Terraza (2003). "Is it possible to study chaotic and ARCH behaviour jointly? Application of a noisy Mackey-Glass equation with heteroskedastic errors to the Paris Stock Exchange returns series". Computational Economics. 21 (3): 257–276. doi:10.1023/A:1023939610962.
  86. ↑ Williams, Bill Williams, Justine (2004). Trading chaos : maximize profits with proven technical techniques (2nd ed.). New York: Wiley. ISBN 9780471463085. 
  87. ↑ Peters, Edgar E. (1994). Fractal market analysis : applying chaos theory to investment and economics (2. print. ed.). New York u.a.: Wiley. ISBN 978-0471585244. 
  88. ↑ Peters, / Edgar E. (1996). Chaos and order in the capital markets : a new view of cycles, prices, and market volatility (2nd ed.). New York: John Wiley & Sons. ISBN 978-0471139386. 
  89. ↑ Mosko M.S., Damon F.H. (Eds.) (2005). On the order of chaos. Social anthropology and the science of chaos. Oxford: Berghahn Books. 
  90. ↑ Hubler, A.; Phelps, K. (2007). "Guiding a self-adjusting system through chaos". Complexity. 13 (2): 62. Bibcode:2007Cmplx..13b..62W. doi:10.1002/cplx.20204.
  91. ↑ Gerig, A. (2007). "Chaos in a one-dimensional compressible flow". Physical Review E. 75 (4): 045202. arXiv:nlin/0701050. Bibcode:2007PhRvE..75d5202G. doi:10.1103/PhysRevE.75.045202. PMID 17500951.
  92. ↑ Wotherspoon, T.; Hubler, A. (2009). "Adaptation to the Edge of Chaos in the Self-Adjusting Logistic Map". The Journal of Physical Chemistry A. 113 (1): 19–22. Bibcode:2009JPCA..113...19W. doi:10.1021/jp804420g. PMID 19072712.
  93. ↑ Dilão, R.; Domingos, T. (2001). "Periodic and Quasi-Periodic Behavior in Resource Dependent Age Structured Population Models". Bulletin of Mathematical Biology. 63 (2): 207–230. doi:10.1006/bulm.2000.0213. PMID 11276524.
  94. ↑ Safonov, Leonid A.; Tomer, Elad; Strygin, Vadim V.; Ashkenazy, Yosef; Havlin, Shlomo (2002). "Multifractal chaotic attractors in a system of delay-differential equations modeling road traffic". Chaos: An Interdisciplinary Journal of Nonlinear Science. 12 (4): 1006–1014. Bibcode:2002Chaos..12.1006S. doi:10.1063/1.1507903. ISSN 1054-1500. PMID 12779624.
  95. ↑ Akhavan, A.; Samsudin, A.; Akhshani, A. (2011-10-01). "A symmetric image encryption scheme based on combination of nonlinear chaotic maps". Journal of the Franklin Institute. 348 (8): 1797–1813. doi:10.1016/j.jfranklin.2011.05.001.
  96. ↑ Behnia, S.; Akhshani, A.; Mahmodi, H.; Akhavan, A. (2008-01-01). "A novel algorithm for image encryption based on mixture of chaotic maps". Chaos, Solitons & Fractals. 35 (2): 408–419. Bibcode:2008CSF....35..408B. doi:10.1016/j.chaos.2006.05.011.
  97. ↑ Wang, Xingyuan; Zhao, Jianfeng (2012). "An improved key agreement protocol based on chaos". Commun. Nonlinear Sci. Numer. Simul. 15 (12): 4052–4057. Bibcode:2010CNSNS..15.4052W. doi:10.1016/j.cnsns.2010.02.014.
  98. ↑ Babaei, Majid (2013). "A novel text and image encryption method based on chaos theory and DNA computing". Natural Computing. 12 (1): 101–107. doi:10.1007/s11047-012-9334-9.
  99. ↑ Akhavan, A.; Samsudin, A.; Akhshani, A. (2017-10-01). "Cryptanalysis of an image encryption algorithm based on DNA encoding". Optics & Laser Technology. 95: 94–99. Bibcode:2017OptLT..95...94A. doi:10.1016/j.optlastec.2017.04.022.
  100. ↑ Xu, Ming (2017-06-01). "Cryptanalysis of an Image Encryption Algorithm Based on DNA Sequence Operation and Hyper-chaotic System". 3D Research (in English). 8 (2): 15. Bibcode:2017TDR.....8..126X. doi:10.1007/s13319-017-0126-y. ISSN 2092-6731.
  101. ↑ Liu, Yuansheng; Tang, Jie; Xie, Tao (2014-08-01). "Cryptanalyzing a RGB image encryption algorithm based on DNA encoding and chaos map". Optics & Laser Technology. 60: 111–115. arXiv:1307.4279. Bibcode:2014OptLT..60..111L. doi:10.1016/j.optlastec.2014.01.015.
  102. ↑ Nehmzow, Ulrich; Keith Walker (Dec 2005). "Quantitative description of robot–environment interaction using chaos theory" (PDF). Robotics and Autonomous Systems. 53 (3–4): 177–193. CiteSeerX 10.1.1.105.9178. doi:10.1016/j.robot.2005.09.009. Archived from the original (PDF) on 2017-08-12. Retrieved 2017-10-25.
  103. ↑ Goswami, Ambarish; Thuilot, Benoit; Espiau, Bernard (1998). "A Study of the Passive Gait of a Compass-Like Biped Robot: Symmetry and Chaos". The International Journal of Robotics Research. 17 (12): 1282–1301. CiteSeerX 10.1.1.17.4861. doi:10.1177/027836499801701202.
  104. ↑ Eduardo, Liz; Ruiz-Herrera, Alfonso (2012). "Chaos in discrete structured population models". SIAM Journal on Applied Dynamical Systems. 11 (4): 1200–1214. doi:10.1137/120868980.
  105. ↑ Lai, Dejian (1996). "Comparison study of AR models on the Canadian lynx data: a close look at BDS statistic". Computational Statistics & Data Analysis. 22 (4): 409–423. doi:10.1016/0167-9473(95)00056-9.
  106. ↑ Sivakumar, B (31 January 2000). "Chaos theory in hydrology: important issues and interpretations". Journal of Hydrology. 227 (1–4): 1–20. Bibcode:2000JHyd..227....1S. doi:10.1016/S0022-1694(99)00186-9.
  107. ↑ Bozóki, Zsolt (February 1997). "Chaos theory and power spectrum analysis in computerized cardiotocography". European Journal of Obstetrics & Gynecology and Reproductive Biology. 71 (2): 163–168. doi:10.1016/s0301-2115(96)02628-0. PMID 9138960.
  108. ↑ Li, Mengshan; Xingyuan Huanga; Hesheng Liua; Bingxiang Liub; Yan Wub; Aihua Xiongc; Tianwen Dong (25 October 2013). "Prediction of gas solubility in polymers by back propagation artificial neural network based on self-adaptive particle swarm optimization algorithm and chaos theory". Fluid Phase Equilibria. 356: 11–17. doi:10.1016/j.fluid.2013.07.017.
  109. ↑ Morbidelli, A. (2001). "Chaotic diffusion in celestial mechanics". Regular & Chaotic Dynamics. 6 (4): 339–353. doi:10.1070/rd2001v006n04abeh000182.
  110. ↑ Steven Strogatz, Sync: The Emerging Science of Spontaneous Order, Hyperion, 2003
  111. ↑ Dingqi, Li; Yuanping Chenga; Lei Wanga; Haifeng Wanga; Liang Wanga; Hongxing Zhou (May 2011). "Prediction method for risks of coal and gas outbursts based on spatial chaos theory using gas desorption index of drill cuttings". Mining Science and Technology. 21 (3): 439–443.
  112. ↑ Glass, L (1997). "Dynamical disease: The impact of nonlinear dynamics and chaos on cardiology and medicine". In Grebogi, C; Yorke, J. A.. The impact of chaos on science and society. United Nations University Press. 
  113. ↑ Mandell, A. J.; Selz, K. A. (1997). "Is the EEG a strange attractor?". In Grebogi, C; Yorke, J. A.. The impact of chaos on science and society. United Nations University Press. 
  114. ↑ Dal Forno, Arianna; Merlone, Ugo (2013). "Nonlinear dynamics in work groups with Bion's basic assumptions". Nonlinear Dynamics, Psychology, and Life Sciences. 17 (2): 295–315. ISSN 1090-0578.
  115. ↑ Redington, D. J.; Reidbord, S. P. (1992). "Chaotic dynamics in autonomic nervous system activity of a patient during a psychotherapy session". Biological Psychiatry. 31 (10): 993–1007. doi:10.1016/0006-3223(92)90093-F. PMID 1511082.
  116. ↑ Metcalf, B. R.; Allen, J. D. (1995). "In search of chaos in schedule-induced polydipsia". In Abraham, F. D.; Gilgen, A. R.. Chaos theory in psychology. Greenwood Press. 
  117. ↑ Pryor, Robert G. L.; Norman E. Aniundson; Jim E. H. Bright (June 2008). "Probabilities and Possibilities: The Strategic Counseling Implications of the Chaos Theory of Careers". The Career Development Quarterly. 56 (4): 309–318. doi:10.1002/j.2161-0045.2008.tb00096.x.
  118. ↑ Thompson, Jamie; Johnstone, James; Banks, Curt (2018). "An examination of initiation rituals in a UK sporting institution and the impact on group development". European Sport Management Quarterly. 18 (5): 544–562. doi:10.1080/16184742.2018.1439984.
  119. ↑ Dal Forno, Arianna; Merlone, Ugo (2013). "Chaotic Dynamics in Organization Theory". In Bischi, Gian Italo; Chiarella, Carl; Shusko, Irina. Global Analysis of Dynamic Models in Economics and Finance. Springer-Verlag. pp. 185–204. ISBN 978-3-642-29503-4. 
  120. ↑ Juárez, Fernando (2011). "Applying the theory of chaos and a complex model of health to establish relations among financial indicators". Procedia Computer Science. 3: 982–986. arXiv:1005.5384. Bibcode:2010ProCS...1.1119G. doi:10.1016/j.procs.2010.12.161.
  121. ↑ Brooks, Chris (1998). "Chaos in foreign exchange markets: a sceptical view" (PDF). Computational Economics. 11 (3): 265–281. doi:10.1023/A:1008650024944. ISSN 1572-9974.
  122. ↑ Wang, Jin; Qixin Shi (February 2013). "Short-term traffic speed forecasting hybrid model based on Chaos–Wavelet Analysis-Support Vector Machine theory". Transportation Research Part C: Emerging Technologies. 27: 219–232. doi:10.1016/j.trc.2012.08.004.
  123. ↑ "Dr. Gregory B. Pasternack – Watershed Hydrology, Geomorphology, and Ecohydraulics :: Chaos in Hydrology". pasternack.ucdavis.edu (in English). Retrieved 2017-06-12.
  124. ↑ Pasternack, Gregory B. (1999-11-01). "Does the river run wild? Assessing chaos in hydrological systems". Advances in Water Resources. 23 (3): 253–260. Bibcode:1999AdWR...23..253P. doi:10.1016/s0309-1708(99)00008-1.

进一步阅读

文章

教科书

半技术和通俗作品

  • Christophe Letellier, Chaos in Nature, World Scientific Publishing Company, 2012。
  • Abraham, Ralph (2000). Abraham, Ralph H.; Ueda, Yoshisuke. eds. The Chaos Avant-Garde: Memoirs of the Early Days of Chaos Theory. World Scientific Series on Nonlinear Science Series A. 39. World Scientific. Bibcode 2000cagm.book.....A. doi:10.1142/4510. ISBN 978-981-238-647-2. https://books.google.com/books?id=0E667XpBq1UC. 
  • Barnsley, Michael F. (2000). Fractals Everywhere. Morgan Kaufmann. ISBN 978-0-12-079069-2. https://books.google.com/books?id=oh7NoePgmOIC. 
  • Bird, Richard J. (2003). Chaos and Life: Complexity and Order in Evolution and Thought. Columbia University Press. ISBN 978-0-231-12662-5. https://books.google.com/books?id=fv3sltQBS54C. 
  • John Briggs and David Peat, Turbulent Mirror: : An Illustrated Guide to Chaos Theory and the Science of Wholeness, Harper Perennial 1990, 224 pp.
  • John Briggs and David Peat, Seven Life Lessons of Chaos: Spiritual Wisdom from the Science of Change, Harper Perennial 2000, 224 pp.
  • Cunningham, Lawrence A. (1994). "From Random Walks to Chaotic Crashes: The Linear Genealogy of the Efficient Capital Market Hypothesis". George Washington Law Review. 62: 546.
  • Predrag Cvitanović, Universality in Chaos, Adam Hilger 1989, 648 pp.
  • Leon Glass and Michael C. Mackey, From Clocks to Chaos: The Rhythms of Life, Princeton University Press 1988, 272 pp.
  • James Gleick, Chaos: Making a New Science, New York: Penguin, 1988. 368 pp.
  • John Gribbin. Deep Simplicity. Penguin Press Science. Penguin Books. 
  • L Douglas Kiel, Euel W Elliott (ed.), Chaos Theory in the Social Sciences: Foundations and Applications, University of Michigan Press, 1997, 360 pp.
  • Arvind Kumar, Chaos, Fractals and Self-Organisation; New Perspectives on Complexity in Nature , National Book Trust, 2003.
  • Hans Lauwerier, Fractals, Princeton University Press, 1991.
  • Edward Lorenz, The Essence of Chaos, University of Washington Press, 1996.
  • Marshall, Alan (2002). The Unity of Nature - Wholeness and Disintegration in Ecology and Science. doi:10.1142/9781860949548. ISBN 9781860949548. 
  • David Peak and Michael Frame, Chaos Under Control: The Art and Science of Complexity, Freeman, 1994.
  • Heinz-Otto Peitgen and Dietmar Saupe(Eds.), The Science of Fractal Images, Springer 1988, 312 pp.
  • Clifford A. Pickover, Computers, Pattern, Chaos, and Beauty: Graphics from an Unseen World , St Martins Pr 1991.
  • Clifford A. Pickover, Chaos in Wonderland: Visual Adventures in a Fractal World, St Martins Pr 1994.
  • Ilya Prigogine and Isabelle Stengers, Order Out of Chaos, Bantam 1984.
  • Peitgen, Heinz-Otto; Richter, Peter H. (1986). The Beauty of Fractals. doi:10.1007/978-3-642-61717-1. ISBN 978-3-642-61719-5. 
  • David Ruelle, Chance and Chaos, Princeton University Press 1993.
  • Ivars Peterson, Newton's Clock: Chaos in the Solar System, Freeman, 1993.
  • Ian Roulstone; John Norbury (2013). Invisible in the Storm: the role of mathematics in understanding weather. Princeton University Press. ISBN 978-0691152721. https://books.google.com/?id=qnMrFEHMrWwC. 
  • Ruelle, D. (1989). Chaotic Evolution and Strange Attractors. doi:10.1017/CBO9780511608773. ISBN 9780521362726. 
  • Manfred Schroeder, Fractals, Chaos, and Power Laws, Freeman, 1991.
  • Smith, Peter (1998). Explaining Chaos. doi:10.1017/CBO9780511554544. ISBN 9780511554544. 
  • Ian Stewart, Does God Play Dice?: The Mathematics of Chaos , Blackwell Publishers, 1990.
  • Steven Strogatz, Sync: The emerging science of spontaneous order, Hyperion, 2003.
  • Yoshisuke Ueda, The Road To Chaos, Aerial Pr, 1993.
  • M. Mitchell Waldrop, Complexity : The Emerging Science at the Edge of Order and Chaos, Simon & Schuster, 1992.
  • Antonio Sawaya, Financial Time Series Analysis : Chaos and Neurodynamics Approach, Lambert, 2012.

外部链接

编者推荐

集智相关课程

复杂性思维2020

非线性动力学与混沌

非线性动力学和混沌理论是系统发展的，从一阶微分方程及其分岔开始，然后是相平面分析，极限环和它们的分岔，最终得到Lorenz方程，混沌，迭代映射，周期倍增，重整化，分形和奇怪吸引。此系列课程包括机械振动，激光，生物节律，超导电路，昆虫爆发，化学振荡器，遗传控制系统，混沌水轮，甚至是使用混乱发送秘密信息的技术。在每种情况下，科学背景都在初级阶段进行解释，并与数学理论紧密结合。


复杂性思维2020

在本课程中张江老师将用一套自己搭建的称为“复杂性阶梯”的框架串联起众多复杂性科学概念，包括混沌、秩序、自催化网络、涌现、混沌边缘、热力学第二定律、分形、网络、自指等等。沿着复杂性阶梯一路攀爬，复杂性层级将逐步提升。生命组织如此，人类组织亦是如此，它们其实都遵循着非常相似的复杂性规律。只不过由于每个系统演化所处的阶段的不同，以及我们每个人看待这些事物的观察视角不同，因而它就会呈现出令人眼花缭乱的复杂性。本课程则带领你透过现象看到本质。


本中文词条由薄荷编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=混沌理论&oldid=9094”