生命之流(7)——流动与时间的赛跑
- 作 者:jake
- 时 间:2008-04
生命之流(7)——流动与时间的赛跑
很早以前,古希腊的哲学家们就开始认识到“万物皆流”是宇宙的本质。这种流变就对 应为一切生命系统甚至非生命系统(例如人类城市)都具备的新陈代谢属性。我们所讨论的 流动系统都具有新陈代谢特征,也就是组成系统的个体单元每时每刻都在更新、都在变化, 但奇怪的是,由这些流变的部分却能构成一个稳健的整体!你、我的身体就是这样的不断流 变的新陈代谢的整体,要知道你身体的细胞平均每隔四年就被更新一次了,那么凭什么说你 还是 4 年前的你呢?因为,你和我还有所有的生命个体一样,我们都是由一些不断流变的 个体所组成的稳定的模式(Pattern)。
非平衡态统计物理是一门认真对待新陈代谢现象的学科,它就是研究各种能量、物质的 流动所组成的开放系统。然而,近百年的非平衡态统计物理的发展却没给我们带来更多的认 识上的飞跃。因为目前科学家们还没有找到适用于所有非平衡系统的通用规律,大部分有意 义的结论仍然局限于一些相对简单的近平衡系统中。
但是,就在这最近的短短 20 年间,一些理论上的新发展可能即将打破这一僵局。一方 面,当越来越多的人开始关注广义的非平衡态现象的时候,人们渐渐领悟到一条所谓的“最 大流原理”可能正在制约着一切非平衡系统的演化;另一方面,随着人们对生态系统的实证 数据的积累,“代谢生态学”正在一点揭示一切广义的新陈代谢现象中的普遍规律。
本章就是要介绍这些非平衡态物理的新进展,和笔者自己提出来的一些理论模型。首先, 我们将小心的讨论最大流原理究竟在说什么,以及它可能的适用范围;其次,我们将给出一 个基于流动的统计力学框架,并与平衡态统计做类比。最后,我们简要介绍一些代谢生态学 的内容,并试图用我们的基于流动的统计框架来探讨代谢生态学中的内容。
最大流原理
让我们放眼周围的大千世界,会发现各种各样的流动仿佛都在加速。例如,随着城市交 通的发展,交通流在不断的加强;随着经济的发展,经济的流动速度:GDP 也在不断的攀升。 孙中山曾说:“人尽其才,物尽其流”,即事物发展的一种必然趋势就是要让流动尽量的通顺、 畅快。
科学家们不会对这类明显的规律视而不见,于是,越来越多的人提出了不同的原理来总 结这类流动加强,一切都在加速的现象。例如,著名的美国生态学家 Lotka(因为提出著名 的捕食者-被捕食者模型,即 Lotka-Volterra 模型而闻名)早在 1922 年就提出了一个猜想, 随着生态系统的演化,生态系统中的总功率,也就是总能量流会被不断加强。随后,另一名 美国生态学家 H.T. Odum 进一步总结了 Lotka 的结论,而提出了一个一般性的原理:“最大功 率原理”来阐释这种生态系统中的能量流加强的现象。随后,生态学界有一批人非常热衷于 寻找生态系统中的各种“目标函数”(生态学家们称其为 Eco-target,有很多有关能量流的函 数都可以充当这个 Target,比如 Exergy,Emergy 等等)。
另外一些与最大流原理研究密切相关的是物理学家。早在 1947 年,著名物理学家普利 高津就提出了一个“最小熵产生原理”以揭示非平衡定态的现象(关于熵产生,我们将在下 一章详细论述)。随后,很多物理学家围绕着熵产生这个函数,提出了各种原理,其中有一 个跟最大流非常接近的原理是最大熵产生原理,我们将在下一章详细讨论这些主题。 近些年来,还有很多人独立地提出了非平衡系统中的各种最大流原理。例如,工程师 Bejan 提出了一个所谓的“构建定律”,指出任何一个非平衡系统都要最大化它内部的流动通 路,从而生长出各种不同的结构。中国天津大学环境学院的柴立和教授和日本东京大学的 Shoji 教授通过研究沸腾液体中的各种气泡的相互作用,而提出了“最大流原理”(Maximum Flux Principle)。
Nature 的自由撰稿人,科普作家:John Whitfield 曾于 2007 年发表在著名生物电子杂志 Plos One 上的一篇文章叫作《Survival of likeliest》,暗示了一个新的自然选择原理:那些能够 把能量流调节到最快速最顺畅的生物体才能获得更大的生存可能性。并且,他明确指出了达 尔文自然选择学说应该以统计物理的基本思想为基础。因此,John Whitfield 暗示了一个作 为自然选择的最大流原理。
还有很多前人积累的工作我们就不一一列举了,但是仔细考察这些“原理”就会发现, 虽然它们表面上都在讨论最大流现象,但是它们的实质却非常不同。首先,这些最大流原理 中被最大化的那个目标函数是不尽相同的;其次,这些原理所适用的范围也是非常不一样的。 因此,可以说,所谓的最大流原理仍然处于一种“群龙无首”的混乱局面,因此,主流科学 界也从来没有认真对待过最大流原理。
面对这样的混乱局面,我们首先有义务对所有这些最大流原理进行总结和归纳。我们将 把最大流原理归结为三个子原理,这三个子原理分别适用于三种不同的条件。但是,统一的 目标函数的问题将留给下一章解决。
最快者生存(Survival of fastest)
在诸多的最大流原理中,John Whitfield所说的“最快者生存”是一条最重要的原理,尽管这条原理相比较其他的原理来说并不那么直观。这条原理之所以重要,一方面是它奠定了一种以统计物理思想为基础的理论;另一方面,它为达尔文的适者生存理论提供了一个合理的基础。另外,我们将指出,很有可能从这条原理出发,我们可以从理论上导出其他的最大流原理。因此,我们将最快者生存原理称之为最大流第一原理(The first principle of maximum flux)。
让我们放眼大千世界,会发现自然选择原理之中的确包含了时间和效率的内容。因此,赢得了时间也就赢得了生存竞争。
让我们考虑两种生物A、B,假如它们同时竞争一种有限的能量资源E,但是这两种生物体处理能量的速度不一样,A快而B慢。那么,很显然,A就会比B更加容易活下去。假如A消化单位能量所需要的时间是T1,而B消化同样能量的时间是T2,并且假设每个生物在消耗完一定的能量之后又会从E获取更多的能量。那么,容易计算,A生物所获取的总能量就是E/T1,B生物是E/T2,而因为T1<T2,所以A生物获得的能量就比B多。所以,A就会比B更容易生存下去。
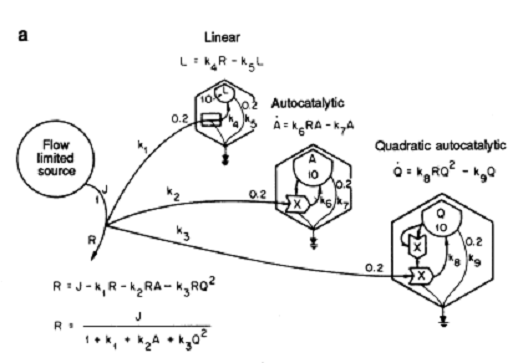
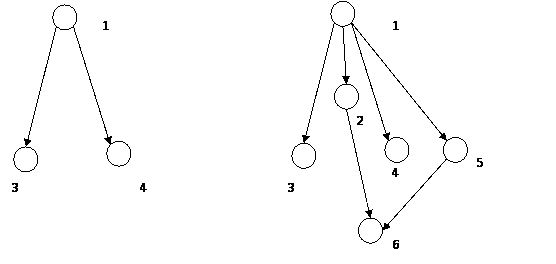
生态学家H.T. Odum曾设计了一个更精细的不同生物体竞争能量流的模型来说明这种最快者生存原理。如图:
在这个例子中,有三种不同的生物来竞争同样的一种能量流资源。这三种生物分别用三个右侧的六边形表示,能量源用左侧的圆圈表示。与上面的例子不同的是,这个能量源不具有固定的能量,而具有固定的能量流速。我们可以把这个能量源想象成一个大的水池,这样每一时刻,都有固定的能量J(常数)流入水池中。而这个水池不具备储存能量的能力,所以没用的能量就会直接转变成废物而流出,这个流出量就是R。
三种生物体都从这唯一的能源获得能量流,并且每个生物体获取能量的方式都不同,它们分别用不同的微分方程来表示。三种生物体也可以看作是一个储存能量的蓄水池,它们体内所包含的能量大小分别用L,A和Q来表示。
这样,对于第一个生物体L来说,它在每周期所获得的净能量是:
[math]\displaystyle{ \dot{L} = k_4 R - k_5L }[/math]
在这里[math]\displaystyle{ \dot{L} }[/math]表示L的变化率,[math]\displaystyle{ k_{4}R }[/math]表示该生物体每时刻摄入的能量流,注意,它跟能量源在该时刻所剩下的能量R有关;[math]\displaystyle{ k_{5}L }[/math]则表示该生物在每时刻消耗的能量流。这样,二者的差就表示每一时刻L的净增长量。同样,其他的两个生物A和Q也是类似,不过他们与L获取能量的方式不同。比如A所获取的能量流不仅与R成正比,而且还与他自身的总能量A成正比,所以随着A增加,它每时刻所获得的能量流入率也增加,这就是说,A这种生物能够主动觅食,当A增加了,它们群体获得能量的能力也会增加。类似的,Q的增长率不仅与R成正比,而且还跟Q2成正比,这样,随着Q的增加,它的获取能量的能力就会比A增加的更快。
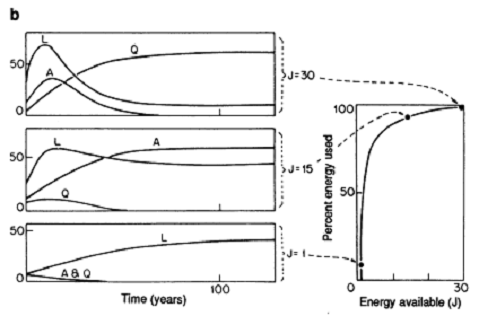
总结来看,该系统中一共有4个变量分别是L,A,Q和R,其中L,A,Q分别用它们的微分方程来计算,R则按照图1左端的方程计算,[math]\displaystyle{ k_{1}, k_{2}, ...,k_{9} }[/math]和J都是常数。对于这样的动力系统,我们不难用计算机模拟的方法研究它。请看下图的模拟结果:
在左图中,我们看到,不同的参数J会导致不同的演化曲线,从而有不同的生物会胜出。当能量流量很小(J=1)的时候,A和Q这两种生物会很快死亡消失,而L这种简单的线性生物胜出。但是,随着J增大(J=15)的时候,A这种比L更复杂一些的生物(因为具备了主动觅食功能)会最终取胜。最后,当J很大的时候(J=30),只有最复杂的生物Q会胜出,其他的生物都灭绝了。右图所表示的是在不同的J取值的情况下,系统中没有被使用的能量流R的大小与总能量流大小J之比。我们看到,随着J的增加,整个系统的能量利用率会越来越高。
Odum这个例子显然更加复杂、精细,它不仅说明了,不同的能量流会对不同的生物造成选择,而且,还说明了不同的能量流会创造完全不同的生态系统。当能量流较小的时候,生态系统会比较简单,因此只有线性获取能量的物种L能生存,但是随着能量流变大,可以存活的物种就会变得越来越复杂,那些能够更加主动获取能量流的物种才会在生存竞争中获胜。
自加速原理
生存竞争往往体现在同等情况下的多个主体和多个系统之间的故事,然而,在更多的复杂系统中,即使不存在同等条件下的多个主体或者系统,我们仍然会看到一种自动加速的现象。例如,在一个地区的经济系统中,随着系统的演化,系统之中的经济、贸易之流会被加强。很显然,对于一个经济系统来说,这里就不存在多个系统之间的生存竞争,也就没有上面所讲的“最快者生存”的那套故事了。但是,最大流现象仿佛仍然存在,因此,我们有必要和上面的第一最大流原理相区分,分别提出第二最大流原理和第三最大流原理。
不失一般性,我们可以把任何一个非平衡的复杂系统抽象为一个输运能量、物质或者货币的网络。如下图所示:
如果我们定义系统的总流量为:
[math]\displaystyle{ F = \sum_{i j} f_{i j} }[/math]
其中[math]\displaystyle{ f_{i j} }[/math]为边i-->j上的流量。这样,如果F在增加,则有可能由多种因素造成的。首先,整个网络的拓扑结构会发生变化从而导致总流量的加强,这是我们下一个即将讨论的第三最大流原理。其次,如果系统的网络结构不发生变化,那么假如系统中输运的物质总量增加了,那么系统的总流量自然也会增加。这些情况都不稀奇,但是还有一种情况是,系统中流动的物质或者能量总量并不发生变化,但是仅仅这些流动物质的流动速度增加了,这被称为第二种最大流原理,也就是我们这里说的自加速原理。 请看下面的例子:
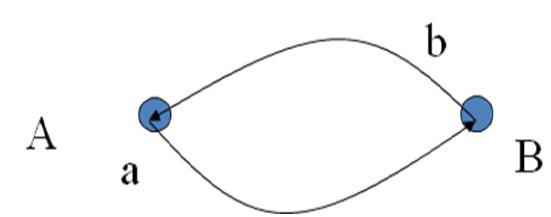
假设一个非常简单的环状输运网络,其中有两个节点A和B,在这个网络上输运着两个物质a,b,并且a,b在输运过程中不会消失也不会增加。假设每一个周期,就会有一单位的a或者b从A跳到B或者从B跳到A。那么10个周期内,我们就会看到从A到B的总流量为ababababab,就是10。
假如这两种物体在网络上运动的速度加快了,那么,在每个周期a可以走两步,这样a跳到B再跳到A,那么同样是10个周期,A到B的总流量就是:ab ab ab ab ab ab ab ab ab ab,即20。在这种情况下,流动于整个网络上的总物质并没有增加(总物质量仍然是a+b),但是由于每一个物质的运动速度增加了,所以网络上的总流量就加强了。
第二最大流原理试图抽象地告诉我们,自然系统的演化会趋向于这样一种自加速现象。我们看到,在经济系统中这种自加速现象是明显的。我们知道,一个宏观经济系统的GDP定义为所有生产价值的总和,然而这种生产价值的计算则取决于对货币流量的累积。也就是说,如果把经济系统中的交易看作一个输运货币的网络,那么GDP就相当于是这个网络上的总的货币流。假如在一段时间内,政府没有发行新的货币,并且假设这个经济系统没有对外贸易,这也就意味着流动于整个网络上的货币总量没有改变。但是我们看到,这个经济系统的总GDP仍然会随着经济系统的蓬勃发展而增加。那么这种新增加的GDP就并不来源于从外界注入的新货币流,而在于等量的货币流在系统之中的流动速度增加了,所以,这种情况下,GDP的增加正是第二最大流原理的体现,也就是一种货币流的自加速现象。
让我们总结一下第一最大流原理,即最快者生存原理和第二最大流原理,即自加速原理,会发现,这两种原理都揭示出了流动与时间的紧密关系。因为无论是哪个原理,它们都在说流动所占用的总时间会越来越少。因为流动本身就定义为在单位时间内,流过某一个点的流量的总和;所以如果系统变快,自然流量就会变大。也就是说流量大和时间快本身就是一对双关语,他们应该是同一硬币的两面。这种认识是非常重要的,我们还会在后面继续探讨这里面的深刻含义。
流与网络的协同演化
我们已经讲述了两种最大流原理,正如上一节的最后一段所述,这两种最大流原理都是一类跟时间紧密相关的现象。但是,在现实世界中,更多的流动现象不仅仅跟时间有关,更多的时候是同时跟时间和空间有关。例如,在经济系统中,往往是一方面系统中存在着货币流的自加速现象;另一方面,系统也存在着新的货币注入和对外贸易,这就使得不仅仅流动在加速,而且流动的总物质也在增加。更重要的是,输运网络本身也会逐渐演化。那么,在这样一种网络拓扑结构和网络上的流动协同演化的系统中,最大流原理就更加复杂了。
让我们先看一个交通网络的例子。我们知道,在一个城市中,车辆流显然是受到交通网络的结构所限制的;但是,从更长远的时间尺度来看,交通流不仅受到网络结构的限制,而且还会反过来影响网络本身。比如市政部门为了缓解交通压力,会拓宽现有的公路,而且还会不断修筑新的公路使得交通流更加顺畅。假如AàB的路段经常会发生交通拥堵,那么,政府就有可能在A和B之间修筑新的公路使得从AàB的交通流增加。因此,粗略来看,公路和交通流耦合演化的系统总是趋向于最大化交通流的方向。
Lotka所提出,Odum进行了扩展的最大功率原理也是在说这样一种流与网络的协同演化现象。我们可以把一个复杂的多物种相互作用生态系统抽象成一个复杂的能量输运网络,那么在这样的网络中,系统的演化就体现为网络拓扑结构的不断变化,Lotka猜想,这样的网络变化必然会最大化系统之中总的能量流。让我们看看下面的例子:
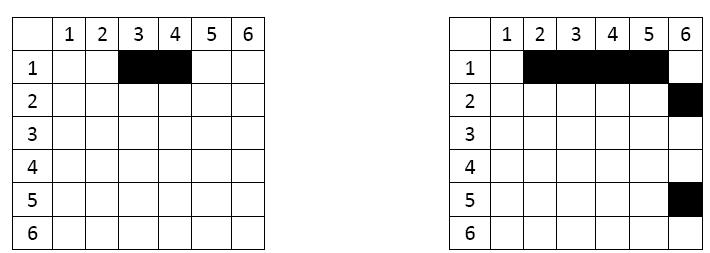
如图5所示,生态系统中的能量输运网络会经历从左图到右图的演化过程。在这个过程中,更多的物种会加入到这个系统之中,从而使得能量流通道会被构建,最终导致总的能量流增加。
我们可以用一种特征空间的方法来表示所有这些物种和物种之间的能量流通路,那么图6中从左图到右图的演化过程就可以对应着图6的一种特征空间中的扩散行为。
如图6,表格中黑色的方格对应着相应的节点之间存在着连接。我们看到,在图5中的网络演化就对应着图7-6中的黑色方格的扩散过程。也就是说,图5中的网络越来越复杂就意味着6特征空间中的黑色方格扩散所占的面积会越来越大。也就是说,这样一种系统的演化行为将不仅仅体现在时间中的加速现象,而更多的体现为空间中的扩散行为。
显然,这种流与网络的协同演化反映了更加普遍的系统现象。例如,在经济系统中,如果把各种产品看作是网络的节点,那么产品之间的交易就对应了网络上的流动。我们会观察到,随着系统的演化,经济体中可用来交易的产品种类也会越来越丰富,从而使得整个经济系统的货币流加强,从而导致了经济的繁荣。这里面,产品越来越丰富也可以看作是一种产品特征空间中的扩散现象。
总结来看,我们可以得出第三条最大流原理:在一个网络和流动协同演化的系统中,网络的拓扑结构会逐渐变化,使得流过系统的总流动增强。
基于流动和时间的统计力学
我们尝试着对各种最大流原理进行归类、总结,以图更加清晰的表述这些原理。但是,这些表述仅仅是把最大流作为一种猜想提出来,而并没有进一步分析为什么会产生这些最大流现象。通过前面几章对平衡态统计物理的回顾,我们发现,最大流原理与平衡系统中的最大熵原理非常相近。最大熵原理说,对于一个任意的封闭的平衡系统来说,系统将朝向最大化熵的方向演化。我们可以回忆那个玻尔兹曼撞球模型,一群小球最终会趋向一种最无序的状态,这种状态的一个特性就是:它们会尽量充满整个容器空间,因此,我们也可以把最大熵原理粗俗的理解为,随机性的小球会最大化的充满所允许的空间。与此类似,在叙述最大流原理的时候,我们已经反复强调了,最大流原理是一种流动和时间的对偶关系,这样一种系统演化的趋势就意味着:随机性的流动会最小化它所需要的时间。因此,这样一种流动和小球的类比,以及时间和空间的类比让我们看到,很有可能存在着一套与玻尔兹曼统计力学相仿的统计力学,只不过这套新的统计力学不是关于小球占领空间的,而是关于流动如何占领时间的。
为了初步领略这种流动与小球,时间与空间的对称性。让我们用一个具体的例子和第五章讲的玻尔兹曼小球模型进行对比。虽然这个例子没有说明最大流原理,但是它清晰地说明了时间和空间之间的对称关系。 例1:(如图7)若干运动员在同一条起跑线上于同一个时刻出发,经过激烈的角逐,最终他们到达终点的时间会呈现均匀的随机分布。
如果我们用运动员起跑在时间上的分布曲线来看,他们近似构成一个尖峰的δ分布,曲线的熵为0。而在终点线上,这些运动员在时间上的分布将会呈现一种最大熵的均匀分布情况。这是我们经常会观察到的现象。 然而,究竟为什么会呈现这样一种现象呢?实际上它是玻尔兹曼小球模型在时间域上的翻版。为了对这个问题进行更正式的讨论,让我们先定义这样一个模型:
假设有一个长方形的跑道如图7-8所示,运动员(左侧的箭头)从同一个起跑点(方框的左侧)出发,跑完整个过程到达同一个终点(方框的右侧)为止。每一个运动员都用一个小箭头表示,也就是说每个运动员都是一个流动过程。图8仅仅是一种示例,表示运动员在不同的时间点上分布在跑道的不同位置。
实际的情况是,每个运动员由于竞技水平的差别而具有不同的速度,这样经过漫长的角逐,速度快的运动员就会先到达终点,速度慢的运动员就晚到达终点。为了模拟这种情况,我们给这群运动员制定下列规则:每个运动员分处于不同的跑道之上,他们彼此之间没有相互作用,他们会保持自己的速度匀速运动到终点。
好了,下面我们就来将这个运动员跑步的模型与玻尔兹曼小球模型进行类比。
图9 玻尔兹曼小球模型随着时间的演化
如图9所示,初始时刻,小球都集中在容器的左下角,随着时间的演化,这些小球开始随机的游走,最终会散布在容器中的所有位置。如图9的最后一张图所示。
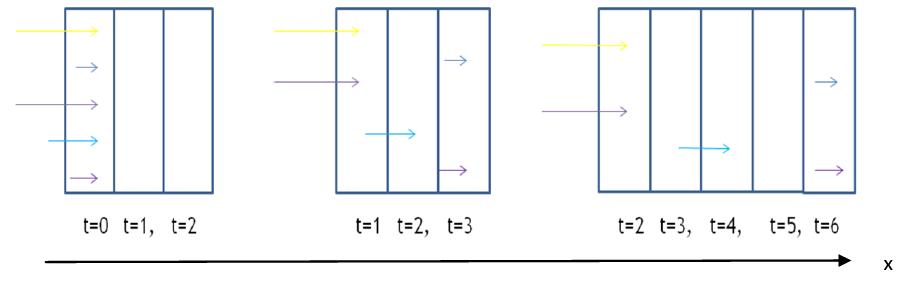
流动模型跟这个小球模型非常相似,只不过需要把小球模型中所有出现时间的地方替换为空间,所有出现空间的地方替换为时间,如图10:
首先,需要说明图7-10画出来的是跑道的不同空间位置上各个运动员在时间上的分布情况。例如,在左侧的第一张图中,这画出来的是起跑点位置各个运动员在t=0,t=1,和t=2三个时间点上的分布情况。显然,在起跑点位置上,所有的运动员全部集中在初始时刻t=0上面。而到了t=1和t=2时刻,由于所有的运动员都运动了,因此都会离开x=0这个点,所以,在这两个时刻没有运动员分布其中。让我们再看图7-10中的第二副图,它表示x=1这个点上,不同时刻t=1,t=2,t=3上面运动员的分布情况。为了清楚,我们用不同的颜色标识了不同的运动员,他们具有不同的速度。假设最快的速度是1个空间单位/时间步,那么黄色和中间蓝色的运动员就会在t=1时刻跑到x=1的位置,也就是他们会分布在t=1这个竖格子里面。同样,下面倒数第二个天蓝色的运动员速度是1个空间格/2个时间步,相当于每2个周期走一个格,这样他就会在t=2时刻到达x=1这个点。同样的道理,第二个运动员和最下面的运动员速度最慢,是1个空间格/3个时间步,所以他们会在t=3这个时刻到达空间位置x=1这个点。最后,所有的运动员在x=1这个位置上不同的时间上的分布情况就如图7-10的中间那张图所示。同样的道理,我们可以画出x=2这个位置上,不同的运动员在不同时间上的分步,我们看到,随着距离逐渐往右推移,各个运动员在不同时间上的分布就会随着速度的不同而越来越均匀。如果计算这些运动员在时间上的分布熵,我们会看到这个熵值会越来越大。这与玻尔兹曼模型中各个小球会尽可能地占领所有的容器空间是完全对应的。
为了更清楚地看清楚这种类比关系,我们列出下面这个对照表:
| 条目 | 玻尔兹曼小球模型 | 流动模型(运动员模型) |
| 系统条件 | 初始条件:所有的小球都集中在容器的左下角 | 边界条件:所有的流动都在同一个时刻出发 |
| 统计的微观对象 | 小球 | 流动(运动员) |
| 演化规则 | 小球按照自己的速度无碰撞的在容器中移动 | 流动在各自的跑道上无碰撞的移动 |
| 守恒性 | 在任意给定时刻,处于所有不同空间位置的小球总数不变 | 在任意空间点上(跑道的不同横截位置),在所有不同时刻经历过的流动总数不变 |
| 系统状态 | 任意时刻,小球在所有容器空间上的分布情况 | 任意空间点,流动(运动员)在所有不同时间上的分布情况 |
| 平衡(最终)状态 | 在最后时刻,所有的小球最均匀的充满容器的所有空间,小球空间分布对应的熵最大 | 在跑道的空间终点上,所有的流动(运动员)都最均匀的充满可能的时间,流动时间分布对应的熵最大。 |
我们看到,玻尔兹曼的小球模型和我们这里的流动模型有着非常漂亮的对称关系,所不同的是,我们需要把玻尔兹曼模型中所有出现小球的词汇都替换成流动,所有出现空间的地方都替换成时间,而所有出现时间的地方都替换成空间。虽然这个例子并不能说明更深奥的道理,但是它至少向我们揭示了,传统的统计物理充其量是一套关于空间的统计力学,而还存在着一套针对流动和时间上的统计力学,还远远没有被人揭示。这个流动模型的例子可以让我们窥视到这套新理论的“一斑”。
虽然运动员跑步的这个例子能让我们看到了统计力学这套方法是完全可以将时间和空间互换的,但是这最终的结论:所有的流动会尽可能的充满整个时间似乎和我们一开始的目标:随机性的流动会最小化它所占据的时间,还相差很远。这种时间上的快速性和统计概率究竟有什么关系呢?我们需要开发新的工具来理解时间和概率的关系。
四维概率
要理解流动和时间的关系,尤其是第一最大流原理:最快者生存,我们必须将概率和速度快慢联系起来。按照统计力学的基本原理,我们所能看到的状态不是必然发生的状态,而是一种最可能的状态,这种最可能的状态对应了一种概率最大的状态。因此,当我们考察最快者生存原理的时候,我们可以同样的把它表述成:自然优胜劣汰保留下来的系统是一种最快的系统,也就意味着越快的系统具有越大的概率。
然而,当我们考察我们熟悉的概率论的时候,会发现,传统的概率更多讨论的是一种空间上的占有现象。
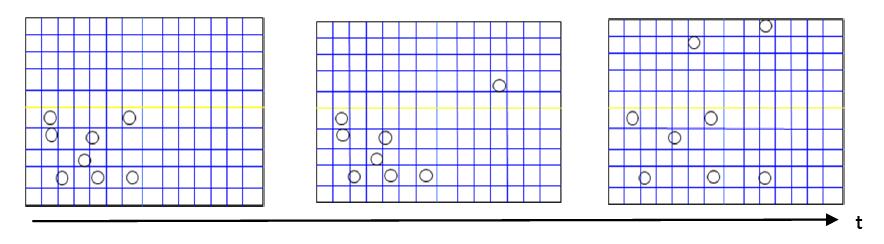
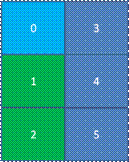
如图11所示,假如在一片土地上种了3种植物,分别用不同的颜色表示出来。其中深蓝色的植物3、4、5占有了更多的空间,所以我们在这片区域中发现深蓝色植物的概率就是1/2,而浅蓝色的植物仅仅占领0号空间,所以它的概率就是1/6。因此,概率越大就说明这种植物所占领的空间就越多。
下面,再让我们看一个完全不同的例子,从而领悟概率大小和速度快慢之间的关系。
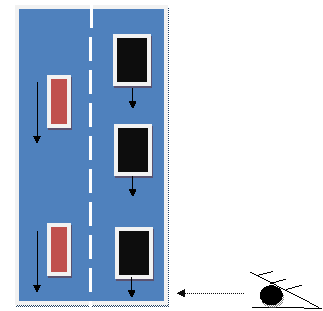
如图12所示,假设一段高速公路上有两种汽车,黑色的大卡车数量略多一些,但他们跑得慢,红色的小轿车数量少一些,但是他们的速度很快。如果观察者坐在直升飞机上,在某一个瞬间进行航拍,就能观察到这段高速公路的全貌,于是这就跟刚才所讲的植物的例子没有什么区别,黑车的概率一定会比红车更大一些。
假设一个观察者并不能看到整个高速公路的全貌,而只能看到高速公路上最下面的横截面上的汽车流动情况,如图12所示。那么由于红车的速度快于黑车的速度,所以在一段观察时间T内,红车的数量就会大于黑车的数量。这是因为,黑车的速度慢,所以在时间间隔T内仅仅有少量的黑车会经过观察者所在的横截面,尽管红车的数量总体来说可能会少一些,但在观察时间T内,由于它运动的速度快,所以就会导致有更多的红车会穿越过观察者所在的截面。所以,在这个例子中,我们看到了运动越快的物体就会拥有更大的概率被观察到。
这个例子酷似一道中学物理竞赛题:下大雨的时候,是不慌不忙的走回家淋雨多还是急急忙忙跑回家淋雨多?假如雨是垂直落下的,那么两种走法淋的雨量是同样多的。这是因为,当我们急急忙忙跑回家的时候,虽然总时间缩短了,但是由于我们运动的速度加快了,这样单位时间内,人体横截面所扫过的面积就会增加,从而当我们速度加快的时候,我们会感受到更大密度的雨滴。这也揭示了为什么飞奔的汽车会比静止的汽车具有更大的概率遭受鸟粪的袭击,所有这些现象都告诉我们运动速度的快慢可以直接影响到我们观察某种事物的概率。
为了更精确、定量的说明这种速度和概率之间的关系,我们需要定义一种新的数学模型,这个数学模型被我称之为四维概率。传统的概率往往仅仅定义在空间维度上,而忽略了时间维度,然而,在四维概率中,一个事件的发生不仅仅跟他所在的空间有关,而且跟它所在的时间有关。我们仍然用前面那个高速公路上的汽车为例子。首先,我们需要将这些汽车以及汽车的运动画在一个包含时间和空间的四维世界中(由于空间被简化成了一维,所以我们仅需要画出一个二维世界就可以了)。
如图13所示,我们将时间画成横坐标轴,把高速公路的空间位置画作纵坐标轴。每一辆运动的汽车都可以看作是这个四维世界中的一条斜的世界线,其上的任意一点表示汽车在某一时刻t运动到了空间上的x点。图中的阴影区域表示的是一次观察所能触及的时间和空间范围。我们知道,在现实世界中,每一次观察只能观察空间上的有限区域,在观察时间上也不可能无限的长,这就造成了每一次观察实际上都是四维世界中的一个区域。 那么在这样的有限区域中,某一个事件被观察到的概率就相当于是这个事件所代表的世界线与观察区域相交的条数占所有可能事件所代表的世界线与观察区域相交的条数的比例。在13图中,显然我们观察到红车的概率就应该是观察区域中代表红车的世界线条数(为3)除以总的可能的世界线条数(为5),所以,观察到红车的概率就是3/5。同样的道理,观察到慢速度的黑车的概率是2/5(为了清晰起见,我们把黑车和红车分别画到了两个不同的空间坐标轴上面了,但实际上,这两个空间坐标轴应该重合。) 显然,某事件的发生概率不仅仅依赖于该事件在空间上的密度,同时也依赖于该事件所代表的世界线运动的速度(即斜率)。速度越大,空间密度越大的事件它的四维概率也就越大。这样,有了四维概率这个模型,我们就能把大概率事件和空间及其时间同时联系起来了
四维概率与代谢生态学
正如本章开篇所说,科学对生物体新陈代谢现象的认识还很初步。然而,近10年来,一门新兴学科:代谢生态学(Metabolic ecology)的横空出世却揭示了生物体新陈代谢中的大量奥秘。虽然,对代谢生态学的各种解释模型和实证规律大量充斥了顶级刊物Nature和Science,但是目前对整个这类现象尚缺乏一个令人信服的理论模型。我们相信,上一节所开发的四维概率模型很有可能为整个代谢生态学奠定理论基础。
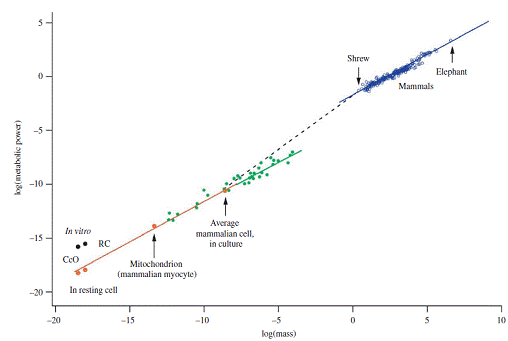
代谢生态学的研究起源于一个被称为Kleiber律的实证规律。如果我们把所有物种的身体重量的对数作为横坐标,把该物种的平均新陈代谢率的对数作为纵坐标,那么每一个物种就会对应于一个独一无二的点,把所有这些点联起来就构成了一条斜率为3/4的直线,如图。
如果将物种的平均身体重量记作M,把它的平均新陈代谢率记作F,那么Kleiber律就可以表示成:
[math]\displaystyle{ F \sim M^{3/4} }[/math]
另外,生物学家们还发现,不仅仅生物体的新陈代谢与它的重量存在着幂律关系,而且很多与时间有关的变量,例如一个物种的平均寿命长短、平均生育年龄、怀孕的时间等等(我们统一记为T),都与该物种的重量M之间存在着1/4的幂律关系,即:
[math]\displaystyle{ TT \sim M^{1/4} }[/math]
而且,更有趣的是,这些规律不仅仅适用于生物体,对于类似人类城市这样的更大的新陈代谢系统来说,也存在着这种普遍的幂律关系(参见Bettencourt等人的文章:《Growth, innovation, scaling, and the pace of life in cities》)。所以,这充分说明代谢生态学所揭示的是新陈代谢系统所共有的规律。
代谢生态学中还有很多的精确的定量规律和统计Pattern,然而这些规律和Pattern却缺乏理论解释。下面,我们将从4维概率的观点来对代谢生态学进行一些非常初步的探讨。这种探讨让我们看出,基于四维时空和流动的统计力学将有可能为代谢生态学的各种实证规律提供基础。
众所周知,我们人类之所以可以观察出一个一个物体,是因为我们能够非常清晰的在空间中划分出这些物体的边界。比如,一张桌子之所以为一个独立的个体,就在于它具有清晰的空间边界。
同样,对于任意一个新陈代谢系统来说,由于系统的组分会无时无刻不在流变,所以,除了界定这个系统的空间边界之外,还需要界定该系统的时间边界,这个时间边界就体现为该系统从出生到死亡的全过程,因此时间边界的大小就是该系统的寿命。由于任何一个新陈代谢个体都是由大量存在着生死现象的更小的细胞构成的,我们可以用下面的图来表示。
如图15所示,生物体都是由很多细胞构成的, ,这些细胞画到四维空间中就是图中的一个黑色圆圈所表示的区域。由于每个细胞都占领一定的空间区域,即它在空间上有一个明确的划分,同时,每个细胞都有自己的寿命,这就导致了他在时间轴t上有了一个明确的时间上的边界,所以,一个细胞就是在四维空间中的一个区域。而对于整个生物体来说,它是由大量的细胞构成的整体系统。原则上讲,这个更大的生物个体的边界需要观察者来界定。比如,从一个细胞的角度讲,它并不能严格区分整个大生物体的内部和外部。然而,我们能够界定出该生物体的边界,这完全是宏观观察作用的一种统计结果。也就是说,从统计上讲,该生物就存在于一个四维空间中的区域内。该区域的空间边界就是我们通常所看到的生物体的边界,而区域的时间边界就是我们熟悉的该生物体的寿命。因此,所谓的新陈代谢生物体只是一个包含了时间的四维空间中的一个区域。而由于每个个体细胞相对于整个生物体来说都是不稳定的,所以我们可以把它们建模成一个一个的随机过程。而生物体本身就是由这些小的四维中的随机过程所构成的一个稳定的四维区域。这就导出了本章最一开始的结论:生物体是由一大堆不稳定的流动的个体所组成的稳定的Pattern。
进一步,把生物体描述成一个四维空间中的区域的另外一个好处是,可以非常简捷的解释Kleiber律,而且还能解释为什么生物体的寿命与体重会呈现1/4的幂律关系。这其实很简单,只要我们假设生物体的质量M并不与它的三维区域的体积成正比,而是与他在四维时空中的区域体积成正比就可以了。这样,对于一个四维的几何体来说,很显然,时间维度会与该四维体的体积呈现1/4的幂律关系,即[math]\displaystyle{ T \sim M_(1/4) }[/math] 。而如果我们再把生物体的新陈代谢看作是生物体所对应的三维空间中的体积,那么自然就有[math]\displaystyle{ F \sim M_(3/4) }[/math]关系成立了。因此,我们得到了一种对代谢生态学的非常简洁的解释。虽然,目前来看这套解释还相当粗糙,然而我们有理由相信,如果将四维概率这套工具进一步扩展,应该可以得到更丰富的结论。所有这些都暗示了一套基于流动和时间的统计力学必然存在!
小结
本章我们主要讨论了两方面的内容,第一是最大流原理,我们将最大流原理分成了三个子原理以澄清这方面文献的混乱局面,分别称为“最快者生存”、“自加速”和网络与流动的协同演化原理。这三种原理分别描述了不同情况下的最大流原理。接下来,我们提供了一整套工具,即基于时间和流动的统计力学,虽然目前这套理论还处于雏形阶段,但是我们相信这套工具应能最终为最大流原理提供很好的理论解释,另外,还可能构成代谢生态学的理论基础。
然而,本章我们并没有给出最大流的任何解释,一方面是笔者对这个最终目标还思考的不成熟,另一方面也为进一步的理论研究工作埋下伏笔,我是希望能够读到这篇文章的读者跟我一起实现这个目标。尽管我没有给出最终的解释,但是我已经对未来前进的方向有了一个比较模糊的图景。下面我来简单叙述一下这张路线图:
首先,我们需要进一步开发四维概率这个工具,把它真正转变成一个可以实用的数学工具。接下来,仿照经典平衡态的统计力学,我们需要建立起一套基于时间和流动的统计力学。而这套新的统计理论必然需要用四维概率作为其基础。其次,我们应该能够攻克第一最大流原理,即最快者生存原理。我们猜想,所谓的最快者生存其实就是流动越快的系统它所具有的四维概率越大,因此,最快者也就是最可能者,我们将可以导出一套达尔文进化论的统计力学解释,从而完成玻尔兹曼的最终夙愿。
之后,就是第二最大流原理,即“自加速原理”,其实这第二原理和第一原理存在着简单的联系。只要我们采取系综的概念,不难发现第二原理其实是第一原理的一个推论。
为了说明第二最大流原理,我们不妨假想,对于一个给定的网络,它的初始条件是给定的,然后我们让它进行演化,这样它就得到了一个演化路径和演化结果。同样,我们可以再一次重复这个网络演化试验,从相似的初始条件开始,但是由于演化规则中存在着随机性,这就导致了一条不一样的演化路径。我们不停重复下去,就会得到一组演化路径。正如上一章中的硬币的例子一样,最终我们实际上得到了一组系统的演化,即统计系综。这组系统可以看作是系综相空间中的一种广义的流动。因此,在这个广义的流动中,这些流动也会遵循第一最大流原理,即最快的流动路径拥有更大的概率。因此,我们看到的最终路径(其实我们并没有作那么多次重复试验,只是随机抽样一次。)就刚好是那条最可能的路径。而这条路经有可能具有自加速现象。
最后,第三最大流原理其实是经典统计力学和基于流动的统计力学的混合物。即在这种系统中,既存在着时间上的最可能者生存,又存在着空间上的最可能者生存,因此随机过程将尽可能地占领更大的空间和更快的时间。很显然,这种最大流原理更具有普遍性,然而,对他的理解需要我们征服前两种最大流原理才能完成。
这一章还有一个微妙的理论问题没有讨论,这就是最大流原理最大化的究竟是什么流?能量流?物质流?信息流?在一个各种各样的流都存在的系统中,究竟哪一种流被最大化了?这个问题其实已经有很好的答案了,也就是说这个被最大化的流不是物质、能量也不是信息,而是熵流。精确地讲,应该是熵流被最大化了,熵被最快速的产生了。我们将在下一章继续讨论这个问题。