自指

古代的符号衔尾蛇，一条吞噬自己尾巴的蛇，表示自指.^[1]

在自然语言或形式语言formal language中，当一个句子、想法或公式指向自己时，就会出现自指现象 Self-reference。（自指的英文Self-reference中，reference有“参照”的意思。）参照可以直接通过一些中间句或公式来表达，也可以通过一些编码来表达。在哲学中，它也指一个主体谈论或指称自己的能力，也就是说，具有第一人称主格单数代词“我”在英语中所表达的那种思想。

自指Self-reference经常在数学，哲学，计算机编程和语言学中被研究和应用。自指陈述有时是自相矛盾的，也可以被认为是递归的。

自指在逻辑、数学和计算中的体现

在古典哲学中，悖论Paradoxes是由自指概念创造出来的，比如全能悖论 omnipotence paradox （上帝悖论）：是否有一个上帝或者全能的存在，可以创造出一个他自己也举不起的石块？

还有埃庇米尼得斯悖论 Epimenides paradox，又称说谎者悖论。这一悖论有许多不同的表述形式，古希腊克里特岛人说的“所有克里特岛人都是骗子”是有记载的最早版本之一。当代哲学有时使用同样的技巧来证明一个假定的概念是没有意义的或者定义不明确的。^[2]

在数学和可计算性理论中，自指(也被称为“不确定性”)是证明许多系统局限性的关键概念。哥德尔定理Gödel's theorem用它来表明，没有一个形式上一致的数学系统可以包含所有可能的数学真理，因为它不能证明某些关于它自身结构的真理。在计算理论中，哥德尔定理的等价表述是停机问题，这一问题表明计算机不能完成关于自身的推理。这些证明关系到数学悖论的悠久传统，如罗素悖论和贝瑞悖论，并最终关系到经典哲学悖论。

在博弈论game theory 中，当博弈双方必须模拟对方的心理状态和行为时，就会出现不确定的行为，导致无穷递归。

在计算机程序设计中，自指发生在反射 reflection 中，程序可以像读取或修改其他数据一样读取或修改自己的指令^[3] 。许多编程语言在某种程度上支持反射，具有不同程度的表达能力。此外，在函数式编程中的递归(与数学递归关系式相关)中可以看到自引用，其中代码结构在计算过程中反向引用自身^[4] 。把自指从潜在的矛盾概念“驯服”到良好的行为递归一直是计算机科学的伟大成功之一，现在经常被 “元语言”机器学习用于编写编译器。使用编译器编译其自身被称为 bootstrapping。无论是使用汇编语言还是使用Lisp 之类的函数式语言，编写让程序可以进行自修改的程序都是可能的，但在实际编程中通常不提倡这样做。计算器硬件使用了触发器中的自指，触发器是数字存储器的基本单位，它随时间推移扩展条件，存储潜在的逻辑自相关矛盾。自指思维在程序员文化中普遍存在，许多程序和首字母缩略词都是以自指的方式命名，这是一种幽默的形式，比如 GNU (“ GNU 不是 Unix”)和 PINE (“ PINE 不是 Elm”)。GNU Hurd 是以一对相互自我指涉的缩写命名的。

Tupper自指公式的Wolfram实现，图像与公式本身一致

Tupper自指公式是一种数学上的奇思妙想，它的图像与其公式本身的样子几乎是一样的。

一种自复制的计算机程序——蒯恩 Quine

在计算机科学中，蒯恩 Quine是一种自复制的计算机程序，也代表了自指的含义。当计算机执行这个程序时，程序会输出自身的代码。例如，利用Python语言编写的一个Quine程序如下如下：

a='a=%r;print(a%%a)';print(a%a)

将以上代码写入文件，然后执行，会发现程序的输出就是程序代码自身：

在生物学中

自指在生物学中表现为自复制 self-replication，正如 DNA 和 RNA 复制机制所体现的那样。康威的生命游戏中有自复制的模型，这些模型启发制造工程系统，比如自复制的3D打印机 RepRap就是一个很好的例子。

在艺术中

自指在文学与电影中同样存在，譬如，一个作者可能在作品本身的背景下提到他自己的作品。

例子包括米格尔·德·塞万提斯 Miguel de Cervantes的《堂吉诃德》，莎士比亚 Shakespeare 的《仲夏夜之梦》，《暴风雨》和《第十二夜》，丹尼斯·狄德罗Denis Diderot 的《宿命论者雅克和他的主人》，意大利卡尔维诺Italo Calvino 的《如果在冬夜，一个旅人》，尼古拉·戈戈Nikolai Gogol 的许多故事，约翰·巴特John Barth 的《游乐园里的迷失》，路伊吉·皮兰德娄 Luigi Pirandello 的《寻找作家的六个人物》，费德里柯·费里尼 Federico Fellini的《八部半》和布莱恩·福布斯Bryan Forbes 的《陋室红颜》。

推理小说作家塞谬尔·迪兰尼Samuel R. Delany在他的小说《新星》和《代尔格林》中使用了这一点。在前者中，卡廷Katin(一个航天小说家)担心一个长期存在的诅咒，即小说家会在完成任何给定的作品之前死去。Nova在中间去世，因此增加了诅咒的可信度，并使读者意识到小说家是故事的作者; 同样地，在《代尔格林》一书中，德拉尼有一个名为Kid(或Kidd，在某些部分)的主角，这个主角的生活就是小说本身的镜像。在科幻恶搞电影《太空炮弹》中，导演梅尔·布鲁克斯Mel Brooks 拍摄了一个场景，反派们正在观看自己故事的 VHS 拷贝，这个场景展示了他们无限地观看自己的“观看自己”。也许最早的例子是在伊利亚特Homer’s Iliad，特洛伊的海伦哀叹道: “为了尚未出生的后代/我们将生活在歌曲中”(出现在歌曲中)。^[5]

艺术中的自指与打破第四道墙和元引用meta-reference的概念密切相关。豪尔赫·路易斯·博尔赫斯 Jorge Luis Borges的短篇小说在许多方面玩弄着自指和相关的悖论。塞缪尔·贝克特Samuel Beckett的话剧《克拉普的最后碟带》完全由主人公自己听录音组成，大部分是关于其他录音的。在20世纪90年代和21世纪初，电影自指是虚幻电影Rubber Reality运动的一个流行部分，特别是在查理·考夫曼Charlie Kaufman的电影《成为约翰马尔科维奇》和改编作品中，后者可以说是把这一概念推动到了鼎盛时期，因为它试图在一个德罗斯特效应剧本化的版本里描绘自己的创作。

各种创世神话援引自指来解决是什么创造了创造者的问题。例如，埃及创世神话中有一个神吞下自己的精液来创造自己。衔尾蛇是一种神话中的会吃自己的龙。

《古兰经》Quran中有许多自指的例子。^[6]^[7]

超现实主义画家勒内·马格利特René Magritte以自指类的作品著称。他的画作《形象的背叛》The Treachery of Images，图片是一个烟斗，但是却包含了“这不是烟斗”的字样，其真实性完全取决于单词 ceci (英语中的“ this”)是指画作所描绘的烟斗，还是指画作本身，抑或“ceci”这个单词，或者是指这个句子本身。

埃舍尔M.C. Escher的艺术也包含了许多自指的概念，比如他的版画作品《画廊》（Print Gallery）。埃舍尔的艺术所作的最后研究包括了其艺术与信息科学、人工智能的关系，这在先前的研究中被忽略了，但是这一点的重要性被侯世达细心的发现了，并写在他赢得1980普利策奖的《Gödel，Escher，Bach：一条永恒的金带》一书中。

在语言学中

一个描述自己的词叫做自体词(或自动词)。这通常适用于形容词，例如英文中“多音节”一词sesquipedalian (即“ sesquipedalian”是一个多音节的的单词) ，但也可以用于其他词类，如 TLA，作为“三个字母缩写”的三个字母的缩写。

A sentence which inventories its own letters and punctuation marks is called an autogram.

一个有自己的字母和句读的句子叫做自拍像autogram。

元语句中的句子内容与宾语中的句子内容相同是元语句的一种特殊情况。这样的句子指的是它自己。然而，这种类型的元语句也可能导致悖论。“这是一个句子。”可以认为是一个自指的元语句，这显然是正确的。然而，“这句话是假的”是一个元句子，它导致了一个自指悖论。这样的句子可能会导致问题，例如，在法律中，元语句使法条的陈述可能会相互矛盾或自相矛盾。库尔特•哥德尔 Kurt Gödel在他的公民身份仪式上宣称，他在美国宪法中发现了这样一个悖论。

自指偶尔会在传媒中出现，比如媒体报道自己的时候，例如BBC报道BBC公司裁员的事件，著名的百科全书维基百科可能被要求提供关于维基百科上的文章。

Fumble rules是一系列好的语法和写作规则，描述这些规则的句子本身违反了这些规则，也是一种自指的规则，比如“避免像瘟疫一样的陈词滥调”和“不要使用没有双重否定”。这个术语是威廉·萨菲尔William Safire在一份她发表的规则列表中创造出来的。^[8]^[9]

在流行文化中

侯世达的书，特别是“Metamagical Themas”和“《GEB》” 使用了许多自指概念，这些书籍在20世纪80年代成功地将“自指”概念引入主流知识文化。Hofstadter定律，做一件事情所用的时间总是比你预期的要长，即使你考虑到了候世达定律。^[10] 是一个自指格言的例子。候世达Hofstadter还提出了“Reviews of this book”的概念，即一本“只包含对自己的评论”的书，这本书已经使用wiki和其他技术实现。候世达的“怪圈”试图将意识映射到自指上，但这在心灵哲学中是少数人的立场。

“递归科幻”或元小说的子类型现在非常流行，以至于在新英格兰科幻小说协会 New England Science Fiction Association的网站上孕育了一个粉丝维护的书目；其中一些有关于科幻电影，一些有关于科幻小说及其作者的文章。^[11]

摄像-屏幕自指模拟

摄像机对着电视机照，再把摄得的图像反传给电视会得到什么？答案似乎应该是什么都没有。集智俱乐部的张江等人通过组织相关的实验，证实这样的一个自指系统能给我们带来非常丰富的复杂图案，一些奇妙的结构会从电视屏幕中源源不断的飞出来。当他们略微调节电视机的亮度、颜色以及摄像机的焦距等等参数以后，却得到了比书中描述的现象更加丰富的图案。而且运用不同的摄像机转动不同的角度会得到完全不一样的结果。

并且，他们经过长期的探索，开发了相应的计算机模拟程序。找到了一种能够近似模拟电视机中动态图像的计算机仿真办法。这就是下面的Java仿真程序。

源代码：Selfref.zip

关于更多的详细流程操作和过程记录可以查看这个词条：摄像-屏幕自指模拟

下面是一些仿真软件做出来的结果（静态图片）：

参见

循环引用 Circular reference -最后一个对象引用第一个对象的一系列引用
彭德罗斯特效应 Droste effect – 递归视觉效果
深处深邃之处 Mise en abyme – 一种现代的技术能够在图像中方式图像本身
第四面墙 Fourth wallー表演艺术的概念，把表演者与观众分隔开来
关于自指的悖论列表
元笑话 Meta-joke
递归 – 以自相似的方式重复自身
递归缩写 – 全称中递归引用它自己的缩写
怪圈Strange loop – 在层级系统中遍历多个层级
this (计算机编程)-在编程语言中，当前运行的代码所属的对象或类
大臭鼠效应 Woozle effect ——是指反复利用缺乏证据的先前出版物，让个人、团体和公众误以为或相信证据存在，而这种非事实会演变成都市传说和事实陈述。
清醒梦 Lucid dreaming——做梦者意识到自己正在做梦的梦

参考文献

↑ Soto-Andrade, Jorge; Jaramillo, Sebastian; Gutierrez, Claudio; Letelier, Juan-Carlos. "Ouroboros avatars: A mathematical exploration of Self-reference and Metabolic Closure" (PDF). MIT Press. Retrieved 16 May 2015.
↑ Liar Paradox
↑ Malenfant, J.; Demers, F-N. "A Tutorial on Behavioral Reflection and its Implementation" (PDF). PARC. Retrieved 17 May 2015.
↑ Drucker, Thomas (4 January 2008). Perspectives on the History of Mathematical Logic. Springer Science & Business Media. p. 110. ISBN 978-0-8176-4768-1. https://books.google.com/books?id=R70M4zsVgREC&pg=PA110.
↑ Homer (1990). Iliad. Translated by Robert Fagles. Penguin Books. p. 207. ISBN 1-101-15281-8.
↑ Madigan, David. The Qur'ân's Self-Image. Writing and Authority in Islam's Scripture.
↑ Boisliveau, Anne-Sylvie. Le Coran par lui-même.
↑ alt.usage.english.org's Humorous Rules for Writing
↑ Safire, William (1979-11-04). "On Language; The Fumblerules of Grammar". New York Times. p. SM4.

↑ Hofstadter, Douglas. Gödel, Escher, Bach: An Eternal Golden Braid. 20th-anniversary ed., 1999, p. 152.

↑ "Recursive Science Fiction" New England Science Fiction Association website, last updated 3 August 2008

资料库

Bartlett，Steven J.詹姆斯（编辑）（1992年）。”自反性：自引用“”中的源帐簿。阿姆斯特丹，北荷兰。[1]

侯世达Douglas Hofstadter（1980年）。哥德尔、埃舍尔、巴赫:一条永恒的金带。纽约，Vintage Books。

雷蒙德·斯莫利安，雷蒙德（1994），“对角化和自指”，牛津科学出版物

Crabtree，Jonathan J.（2016年），“丢失的初等数学逻辑和绑架Kaizen的Haberdasher”，《维多利亚数学协会（MAV）年会论文集》，53，98-106，{ISBN |978-1-876949-60-0}

编者推荐

课程推荐

复杂性思维2020

张江老师作为复杂性思维的布道者，在复杂性科学的科普上准备了很多的适合于初学者了解的科普内容和视频，将复杂性科学的概念和生活紧密结合，同时又能有趣的阐述晦涩难懂的概念，非常值得学习。

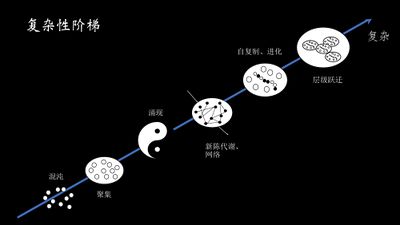
复杂性思维2020

本课程中，张江老师将用一套自己搭建的“复杂性阶梯”的框架串联起众多复杂性科学概念，包括混沌、秩序、自催化网络、涌现、混沌边缘、热力学第二定律、分形、网络、自指等等。沿着复杂性阶梯一路攀爬，复杂性层级将逐步提升。生命组织如此，人类组织亦是如此，它们其实都遵循着非常相似的复杂性规律。只不过由于每个系统演化所处的阶段的不同，以及我们每个人看待这些事物的观察视角不同，因而它就会呈现出令人眼花缭乱的复杂性。本课程则带领你透过现象看到本质。

解读《GEB》

解读《哥德尔、艾舍尔、巴赫——集异璧之大成》

张江老师曾在多次讲座中必推荐的一本书，就是来自侯世达的《哥德尔、艾舍尔、巴赫——集异璧之大成》，这本书对他产生了非常深远的影响，是他走向复杂性科学的启蒙之作，但是这本巨著内容详尽但不是那么容易理解，为了让大家更好的阅读这本书，他从自身的阅读经验出发，给出了一些方法并且对这本书做了一个大致的解读：解读《GEB》

人的创造力VS人工智能

在本课程中，集智俱乐部邀请了《GEB》的作者侯世达先生，来分享他在将近40年的人工智能领域中的感悟和思考，透过Machine Translation这个话题来深入探讨人的创造力和人工智能的话题。

书籍推荐

系统中的观察者(5)——自指

在北京师范大学系统科学学院的教授张江在他的《系统中的观察者》系列中有一章专门介绍了自指这个概念，并且从原理、语言、程序等不同方面介绍了自指的原理和应用，并且提出了观察者理论，推荐大家深度的了解和学习。

自复制自动机理论 Theory of Self-reproducing Automata

这本书的意义不仅仅在于它实际上开创了“人工生命”、“细胞自动机”等多门复杂性研究的分支。更重要的是，该书将“自我复制”作为生命的一个本质特征加以数学建模的研究。而这套理论和可计算性理论、歌德尔定理以及热力学深深地联系到了一起。这一点也许对于我们研究复杂系统的人来说仍具有重要的意义。其中，5篇讲座的讲稿为该书最重要的部分。这5篇文章不仅仅预测了复杂性科学未来100年的发展方向（事实上很多领域已经验证了von Neumann的预言），而且还指出了生命逻辑最核心的奥秘：热力学、信息论与自指之间的深刻联系。

《自复制自动机理论》电子版

本中文词条由水流心不竞用户参与编译，三奇同学审校，思无涯咿呀咿呀编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

[1] Soto-Andrade, Jorge; Jaramillo, Sebastian; Gutierrez, Claudio; Letelier, Juan-Carlos. "Ouroboros avatars: A mathematical exploration of Self-reference and Metabolic Closure" (PDF). MIT Press. Retrieved 16 May 2015.

[2] Liar Paradox

[3] Malenfant, J.; Demers, F-N. "A Tutorial on Behavioral Reflection and its Implementation" (PDF). PARC. Retrieved 17 May 2015.

[Drucker2008-4] Drucker, Thomas (4 January 2008). Perspectives on the History of Mathematical Logic. Springer Science & Business Media. p. 110. ISBN 978-0-8176-4768-1. https://books.google.com/books?id=R70M4zsVgREC&pg=PA110.

[5] Homer (1990). Iliad. Translated by Robert Fagles. Penguin Books. p. 207. ISBN 1-101-15281-8.

[6] Madigan, David. The Qur'ân's Self-Image. Writing and Authority in Islam's Scripture.

[7] Boisliveau, Anne-Sylvie. Le Coran par lui-même.

[8] t.usage.english.org's Humorous Rules for Writing

[9] Safire, William (1979-11-04). "On Language; The Fumblerules of Grammar". New York Times. p. SM4.

[10] Hofstadter, Douglas. Gödel, Escher, Bach: An Eternal Golden Braid. 20th-anniversary ed., 1999, p. 152.
v
t
e
Inline tags
Attribution

{{Attribution needed}}

{{By whom}}

{{Weasel-inline}}

{{Which?}}

{{Who}}

Citation

{{Better source}}

{{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

{{Citation needed (lead)}}

{{Failed verification}}

{{Full}}

{{Primary source-inline}}

{{Request quotation}}

{{Retracted}}

{{Third-party-inline}}

Incomplete

{{Author missing}}

{{Author incomplete}}

{{Date missing}}

{{ISBN missing}}

{{Page needed}}

{{Publisher missing}}

{{Title incomplete}}

{{Year missing}}

{{Dead link}}

Content

{{Contradict-inline}}

{{Contradiction-inline}}

{{Dubious|talk page section name}}

{{Examples}}

{{Inconsistent}}

{{List fact}}

{{Lopsided}}

{{POV-statement}}

Date and place

{{Clarify timeframe}}

{{Quantify}}

{{Update after}}

{{Update-small}}

{{When}}

{{Where}}

{{Year needed}}

Wikification

{{Disambiguation needed}}

{{Pronunciation needed}}

Wording

{{Ambiguous}}

{{Awkward}}

{{Buzz}}

{{Clarify}}

{{Clarify span}}

{{Definition}}

{{Elucidate}}

{{Expand acronym}}

{{Technical-statement}}

{{Vague|optional message to be displayed on mouseover}}

{{Why?}}

Category

[11] v

[12] t

[13] e

[14] {{Attribution needed}}

[15] {{By whom}}

[16] {{Weasel-inline}}

[17] {{Which?}}

[18] {{Who}}

[19] {{Better source}}

[20] {{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

[21] {{Citation needed span}}

[22] {{Reference necessary}}

[23] {{Citation needed (lead)}}

[24] {{Failed verification}}

[25] {{Full}}

[26] {{Primary source-inline}}

[27] {{Request quotation}}

[28] {{Retracted}}

[29] {{Third-party-inline}}

[30] {{Author missing}}

[31] {{Author incomplete}}

[32] {{Date missing}}

[33] {{ISBN missing}}

[34] {{Page needed}}

[35] {{Publisher missing}}

[36] {{Title incomplete}}

[37] {{Year missing}}

[38] {{Dead link}}

[39] {{Contradict-inline}}

[40] {{Contradiction-inline}}

[41] {{Dubious|talk page section name}}

[42] {{Examples}}

[43] {{Inconsistent}}

[44] {{List fact}}

[45] {{Lopsided}}

[46] {{POV-statement}}

[47] {{Clarify timeframe}}

[48] {{Quantify}}

[49] {{Update after}}

[50] {{Update-small}}

[51] {{When}}

[52] {{Where}}

[53] {{Year needed}}

[54] {{Disambiguation needed}}

[55] {{Pronunciation needed}}

[56] {{Ambiguous}}

[57] {{Awkward}}

[58] {{Buzz}}

[59] {{Clarify}}

[60] {{Clarify span}}

[61] {{Definition}}

[62] {{Elucidate}}

[63] {{Expand acronym}}

[64] {{Technical-statement}}

[65] {{Vague|optional message to be displayed on mouseover}}

[66] {{Why?}}

[11] "Recursive Science Fiction" New England Science Fiction Association website, last updated 3 August 2008

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

自指

目录

自指在逻辑、数学和计算中的体现

一种自复制的计算机程序——蒯恩 Quine

在生物学中

在艺术中

在语言学中

在流行文化中

摄像-屏幕自指模拟

参见

参考文献

资料库

编者推荐

课程推荐

复杂性思维2020

解读《哥德尔、艾舍尔、巴赫——集异璧之大成》

人的创造力VS人工智能

书籍推荐

系统中的观察者(5)——自指

自复制自动机理论 Theory of Self-reproducing Automata

导航菜单

搜索