“生命之流(6)——系统之流”的版本间的差异
| 第25行: | 第25行: | ||
让我们再来看一个物理学中的著名实验:贝纳德对流。 | 让我们再来看一个物理学中的著名实验:贝纳德对流。 | ||
| − | [[File: | + | [[File:600px_200885112249130.jpg |600px |thumb |center |图6-2 贝纳德对流试验]] |
如图6-2(b)所示,给一个装有薄层液体的容器底部加热,上部分是敞开的,允许热量从上面跑出去,液体的上下表面保持一定的温度差△T。当△T高到一定程度的时候,该水面会形成如6-2(a)图所示的漂亮的六角格花纹。这些漂亮的花格是由大量分子通过协调、整体的对流运动而形成的有序结构。 | 如图6-2(b)所示,给一个装有薄层液体的容器底部加热,上部分是敞开的,允许热量从上面跑出去,液体的上下表面保持一定的温度差△T。当△T高到一定程度的时候,该水面会形成如6-2(a)图所示的漂亮的六角格花纹。这些漂亮的花格是由大量分子通过协调、整体的对流运动而形成的有序结构。 | ||
2021年3月12日 (五) 23:13的版本
- 作者:jake
- 时间:2008-04
生命之流(6)——系统之流
开放、非平衡系统与流动
可能你已经厌烦了热力学和熵的讨论,因为“热”和“熵”这两个名字总会给人一种不舒服的感觉。的确,当我们把热力学第二定律应用到整个宇宙身上——按照目前人们对宇宙的理解,宇宙本身是一个孤立的系统,即没有物质和能量注入——整个宇宙将演化到一个熵最大的状态,这个状态有一个臭名昭著的名字:“热寂”。如果说万事万物都有方向和目的的话,那么第二定律就告诉我们,这个目的就是热寂。
问题的关键在于:热力学第二定律描述的是孤立系统,尽管整个宇宙很可能是一个孤立系统,但是宇宙中的任何一个局部从严格上来说,都是开放的系统,能量或者物质都不可避免地流进局部系统之中。因此,当我们分析一个开放系统的时候,它实际上更可能处于一种非平衡的状态,即外界的物质和能量的流入驱使着系统不断地演化。所以,热力学第二定律所描述的“热寂”情况并不实用,因为我们面临的实际系统很少处于绝对的孤立且平衡的状态。我们必须从平衡态的世界跳到非平衡态的世界。
当我们放眼非平衡世界的时候,奇妙的秩序开始映入眼帘。我们可以做一些非常简单易行的小试验。把你家的蓄水池装满水,然后打开水池底下的阀门,你会看到水慢慢地从阀门中流出去。如果阀门开口不大,则水流得会很平静,而当阀门开口大到一定程度的时候,池子中的水就会形成漩涡,这种漩涡呈现出某种漂亮的弧形有序结构。如果你再打开水龙头往池子里注入水,使得流入水的速度=流出水的速度,那么你就能够得到稳定的漩涡结构了(图6-1)。
让我们再来看一个物理学中的著名实验:贝纳德对流。
如图6-2(b)所示,给一个装有薄层液体的容器底部加热,上部分是敞开的,允许热量从上面跑出去,液体的上下表面保持一定的温度差△T。当△T高到一定程度的时候,该水面会形成如6-2(a)图所示的漂亮的六角格花纹。这些漂亮的花格是由大量分子通过协调、整体的对流运动而形成的有序结构。
注意,在这个系统中,没有物质的流入流出,而仅仅是能量的流入、流出,因此,我们看到能量流也可以创造有序。
然而,什么是能量流呢?我们都已经熟悉了能量的概念,例如,滚动的小球携带着动能,当小球滚动到粗糙的平面上,小球携带的动能就转变成了热能。然而,在非平衡系统中,我们关注的不再是物质携带的“静止”的能量,而是能量在不同物体之间的转换过程本身,这些能量的转换过程构成了能量流。
让我们来看一个简单的例子,假设有一排静止的小球放在光滑平面上,如图:
当我们给最左边的小球赋予一个初速度v,小球开始往右运动,与第二个小球发生碰撞,如果两个球质量相同,则他们发生速度交换,第一个小球停下来,第二个小球继续以速度v往右滚。第二个小球又碰撞第三个小球……。
我们知道运动的小球携带着动能1/2 mv2,那么当第一个小球和第二个碰撞的时候,第一个小球的动能1/2 mv2就传递给了第二个小球,同样第二个小球把相同的能量传递给了第三个小球……。物质在转化的时候是守恒的,这就意味着,当我把我手上的100块钱给了你以后,我的100块没了,你多了100块,而100块钱本身并没有消失。但是,能量毕竟不是物质,所有小球碰撞过程中传递的是一种“运动的能力”,而不是具体的物质。但因为能量守恒,第一个小球的运动能力没了,等量的能量就传递给了第二个小球。所以,这种运动能力的转移过程就可以看作是能量的流动。
具体说,能量流就发生在能量在两个小球之间的转换过程。所以第一个小球碰撞第二个小球,就会有一股能量流从球1流到球2。如果我们在左边不停的加入速度v的小球进去,并把新加入的小球同样命名为1(因为小球之间不可分辨),把原来的小球1看作是2……。那么,我们就会看到一股持续不断的能量流流到系统之中,即1到2的能量流会被不停地重复,同样2到3的能量流也会不停地重复。在这种情况下,用能量流来描述这个系统就会更加方便了,这个系统就好像一条小河,有源源不断地水流流进。如图6-4所示
当然,在小球例子中能量流并没有创造什么有序结构,因此能量流仅仅是产生有序的一个必要条件。至于能量流与有序结构的关系,我们将在第7、8章详细讨论。下面,我们需要进一步了解有关能量流的知识。
生物圈与能量流
从能量流的角度不仅可以理解诸如小球、贝纳德对流这样的简单物理过程,还可以理解整个生物圈的一切生命过程,甚至包括我们人类的生产活动。因为整个地球生物圈就是一个能量流动、物质循环的过程。如图:
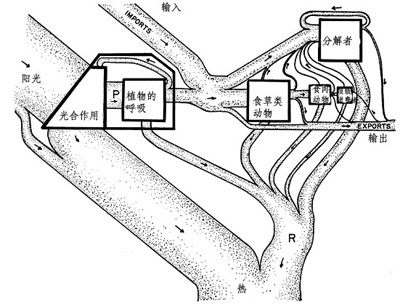
当我们放眼整个地球生物圈的时候,实际上主要关注两种过程。一种是能量流动,另一种是物质的循环。我们都知道,地球上的主要能量来源就是太阳。太阳内部因为热核反应而产生出每秒3.9x1026焦耳的能量,其中只有一小部分入射到地球表面。平均来讲,地表每平方米在每秒钟接收到的太阳辐射能量将近1400焦耳。也就是说,地球实际上浸泡在一个太阳辐射的能量流的海洋中。太阳的能流流入地球生物圈系统之后就会发生一系列的转化过程。这一系列过程就好像一系列的小球碰撞一样,能量以不同的形式转变成另外一种形式。最后,因为热力学第二定律,所有的能量都要以废热的形式辐射到宇宙空间中。正如小球的例子一样,我们可以把能量流理解为一种抽象的“运动能力”,或者是“做功能力”的转移和传递,所以,我们可以假想一个能量粒子(它并不是物质,而是一种纯能量),考察它在整个地球生物圈中的运动过程。
我们不妨把这个能量子命名为小r,它可以呈现出各种不同的能量形态。开始,小r被太阳的热核反应释放出来,一路颠簸,终于来到了地球表面。当小r辐射到地球的时候,会有很大的概率打到土地表面或者海洋中,这样小r要么被反射出去(进入宇宙太空),要么被这些表面吸收,而变成热能。当然,很有可能小r不幸地打到了某植物的绿叶上,这样,它仍然会有近76%的概率被植物反射出去而没有吸收。当然如果它足够倒霉,那么它会有近24%的可能性被植物绿叶吸收而进行光合作用(图6-6)。
(图中管道的粗细表示能流的大小,图中的输入表示从该系统的邻近区域由于扩散或者物质的流动或者动物的迁徙而流入该区域的能量,输出表示该区域流向其他区域的能量)
一般来讲,光合作用是一种复杂的化学反应过程,它可以简化成方程式:
其中CH2O表示糖类有机物。所以植物的光合作用就是把水和二氧化碳在光照的条件下转变成糖和氧气的过程。在这个反应中,能量发生了转变:从光能转变成了糖类中所包含的化学能以及一部分废热。这就好像是一个小球撞击到另一个小球的时候能量发生转移一样。我们可以假设能量子小r并没有变化,而是被转移到了糖类的大分子中,小r后面的历程就一直跟随着糖分子走,所以我们把这个由r转化成的糖分子也叫做糖分子小r。
接下来,糖分子小r可能被植物自己的呼吸作用而分解掉(再次转变成废热),又有近40%的可能性被一直储存在该植物体内。这棵植物(草)有可能倒霉地被兔子吃掉,因而小r就以植物生物量的身份转变成了兔子体内的生物量(兔子肉)。同样,兔子也会由于呼吸作用或者其他的活动(例如跳跃、奔跑、繁殖后代等等)而把糖小r燃烧掉变成热量排出。但是这只倒霉的兔子也可能被狼吃掉,于是小r就有16%的概率再次转移到狼体内(变成狼肉)。没过几天,这只吃了小r的狼可能倒霉的死掉了,那么小r又可能被土壤中的细菌(分解者)抓到,于是细菌把小r分解掉转变成废热,同时把糖小r中的碳元素还原为无机物(CO2),再次返回到环境中。
不过糖小r也可能经历另外一种命运,死掉的狼并没有完全被细菌分解掉,而是经过多年的沉积作用而变成了地里面的石油。于是小r就变成了一滴石油。若干年后,埋藏在石油中的小r又可能会被某石油厂采集到,从而进入了人类社会的工业世界。这滴包含了小r的石油又可能被热电厂转变成电能。这样,电能小r通过高压输电线路输送到你的个人电脑里,于是你的电脑为了打开本文档而进行了一次CPU运算,这次CPU运算终于把电能小r转变成了废热而迷失到空气中。
实际上,关于能量子小r的故事还没有讲完,因为根据热力学第一定律,能量是不会消失的,所以即使小r转变成了热量,它仍然可以体现为分子的运动动能而存在。但是,根据热力学第二定律,其它形式的能量可以转变成热,但是热不能转变为其它能量,所以这些迷失在环境中的热能不可能再次流到我们关心的生物圈系统中。
任何能量转移过程都要伴随着热量的损失,所以,在非平衡态系统中,热力学第二定律扮演的角色就像是一个收税的政府官员。热量一旦产生就不能再被利用,所以它相当于一种绝对的能量流出。这就好像是在经济系统中,国家向每一次交易行为都征税,从而导致每次货币转移都必然伴随着一定量的货币流出而转变成税收一样。在图6-6中我们看到,能量流中有很大部分都转变成了热量,这相当于大自然这个税收官非常苛刻。大自然的能量流转换过程必须非常努力才能让仅有的可用能量向食物链的高端转换。
物质流动与能流价值
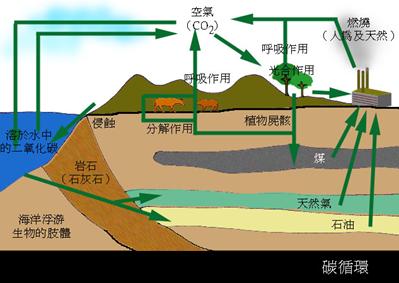
在地球生物圈中,另外一种流动过程就是物质的循环。从物质角度来讲,地球生物圈可以近似看作一个封闭的系统,即几乎没有物质的流入和流出。不同的化学、生物形态仅仅是一些元素的不同组合形式而已。例如,碳是一种地球生物圈中的重要化学元素。虽然碳元素的总量是守恒的,但是它会以不同的物质形态体现,如:二氧化碳气体、糖类物质、石油、大理石等等都是包含碳元素的化学物质。因此,整个物质循环过程就是在能量流的驱动下完成的由各种化学元素(主要是碳、氢、氮、氧等)不断拼接、重组而形成新化学物质的过程。图6-7就是一个生物圈碳循环的简单示例:
与能量流动不同的是,物质的流动往往都是可见的。例如生态学家们可以通过碳的同位素来跟踪某碳原子在整个生态圈中的流动过程。然而,对于能量来说,这种追踪就是不可能的。因为能量是一种抽象的描述变化能力的量,它不能体现为具体的有形物质。
既然能量流是不可直接观测的量,那么物质的流动过程能否反映出能量流的情况呢?答案是肯定的,因为随着能量往食物网高端流动,凝固这些能量的物质形态就会变得越来越复杂。从生物化学的角度来讲,高等生物体(消费者)的生物量要比低等生物体的生物量具有更复杂的分子物质结构。而反过来,当高等生物体把复杂的分子分解成相对简单的分子结构的时候往往都会释放掉储存于复杂分子中的化学能。
实际上,任何一种生物的新陈代谢都可以归结为两种过程,我们可以形象地把它们称为“充电过程”和“放电过程”。在充电过程中,系统会从外界吸收能量,并把它们用更复杂的物质结构储存起来。在放电过程中,系统会利用分解复杂的物质而把储存的能量释放掉,以便完成自己想要做的事情。不仅仅是针对生物体,很多自然或者人工过程都可以看作是新陈代谢的充电和放电过程。例如,给一辆汽车加油就是一种储存能量的充电过程,汽车在马路上奔跑就是一种释放能量的过程。这种广义的新陈代谢甚至可以用来描述更大尺度的系统,例如人类城市。我们知道城市在每时每刻都需要外界的能量和物质的输入,同样,它还不断地以各种各样的人类活动方式把输入的能量和物质释放掉、燃烧掉。
从食物链的角度看,能量流越往食物链的顶端流(往高级消费者的方向流)就相当于创造越复杂的物质,从而这一直是充电的过程。虽然从能量流的角度看不出高级和低级的区别,但是从物质的复杂性角度看,不同的能量流就有了价值之分。往食物链顶端流动的能量被用来充电,因此食物链高端的物质储存的能量价值也就越高。
更有意思的是,要生成一单位的高级能量往往需要大量的低级能量。例如,每凝结一克食草动物的生物量,就需要有100克的植物生物量的供给,换句话说,100克的植物生物量才能与1克的食草动物生物量相当,这是因为兔子要捕食大量的草才能维持一只兔子的生存。同样,可能需要10只兔子才能喂饱一只狼,所以一克狼的生物量相当于10克兔子的生物量。随着我们往食物链顶端攀升,物质的复杂性升高,它也就需要越来越多的低级物质供给。假如我们承认人类是处于食物链的最顶端的话,那么人类文明创造的一小点物质(例如一个芯片)就凝结了大量的食物链底端的物质和能量。所以,虽然芯片进行运算消耗的能量绝对值很小,但是这小点能量消耗的价值却很高,因为它是靠牺牲大量低层的能量完成的。
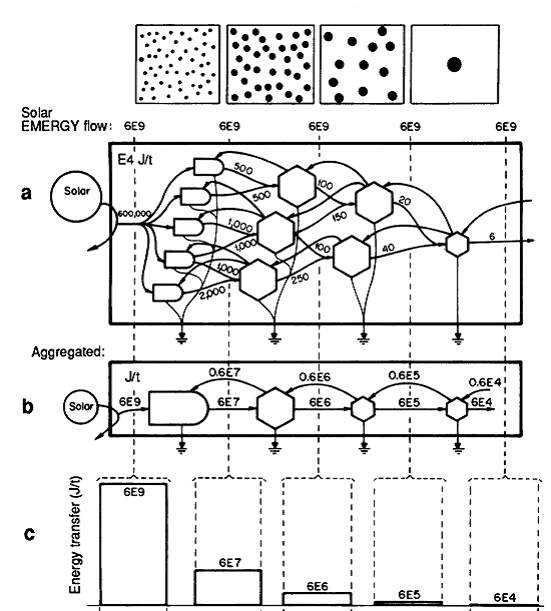
从空间上看,处于食物链高端的生物会占领较大的栖息地,所以在一片森林中,你会发现大量的草和树木,而食草类动物例如兔子就少得多,而吃兔子的老虎则可能整片森林就有一只。著名生态学家Odum很早就注意到了这些能量、物质流模式,并把它们概括成类似下面的图:
其中上面的第一幅图表示相应层级生物的栖息地,从左到右分别是植物、食草类动物、食肉类动物、二级食肉类动物。下面的a,b,c相应的为食物网、聚集之后的食物网、以及每两个层级之间的能量转换大小。能量流的反馈可以认为是高级生物为了捕食低级生物而消耗的能量(见参考文献Odum 1988)。
Odum提出了很多有价值的概念来描述能量流模式的层级性,但是直到最近,人们才发现可以用一些幂率关系来精确定量的描述这种层级性,这就是近年来发展快速的“尺度生物学”(Scaling biology)研究的内容(请看参考文献:Scaling Biology)。
广义的流
到此,我们已经得到了一种新的看待整个复杂系统的研究范式:能量流。但是,这种研究范式总让人感觉有很大的缺陷。虽然说所有事物的存在都必须由能量流来推动,但是很多问题不能仅仅归结为能量流。例如,我们要解释生物的遗传和进化,就不需要把视角降低到底层的能量流,而只需要关注A,G,C,T组成的序列就可以了。我们要解释人类社会,最方便的视角是从经济系统进行认识,而不一定非要还原到能量流。所以,似乎能量流的视角过于还原论了。
不过,当我们把问题看“透”,就会发现,实际上能量流范式给我们带来的启发可以泛化到一类更广义的问题:流。通过流动这个视角去看待复杂系统就会发现能量流仅仅是广义流动的一种特殊形式。
在经济系统中,货币流可以充当和能量流非常相似的角色。如果我们把经济系统中的大大小小的企业看作是生态系统中的物种,那么经济消费者就好像是太阳。因为消费者持有货币,他们可以把货币流源源不断地注入经济系统中。这些企业对货币的需求就仿佛是物种对能量的需求,因为货币就是粮食,没有了钱,任何企业都不能活下去。企业和企业之间还可以通过交易实现货币的流通就好像物种通过捕食而实现能量在物种之间的传递一样。单个的企业也跟单个的生命一样需要新陈代谢。一方面,企业要获得货币流的注入并把它们存储起来(充电),另一方面,企业又要把货币花出去,购买一些劳动力或者原材料以便再生产(放电),从而获得更多的货币。
在人体中,血液(尤其是动脉血)充当的角色和生态系统中的能量流也有非常相似的特征。首先,人体作为一个整体系统要能调节、整合所有的器官、组织,就一定要有某种共同的机制把所有的子系统串联起来,这就是血液的价值所在。同样,心脏的作用就像是太阳一样,它是整个血液系统的能量源泉。每个器官都在心脏的带动下不断进行舒张、收缩,从而完成一个又一个的新陈代谢循环。它们从动脉血中吸收进有用的能量,而往静脉血输出废物。所以,人体就是一个小生态系统。
信息的传播也可以看作一个信息的流动过程。例如,在课堂上,老师的授课就是唯一的信息来源,而所有的学生就是接收信息的主体。课堂与生态系统之间的类比的确有些牵强,不过当我们把整个知识传播体系看成是生态系统的话,那么这个比喻就会非常生动。例如,具备高度知识创新性的个人或者团体就是知识的生产者。接受了这些信息的人就好像知识的消费者。有些人接受了信息之后又会把它们再次传播给别人,那么接受转载信息的人就像是知识的二级消费者。每个社会上的个体既需要知识,同时本身又可以再加工知识而把一些信息传递给别人,这就相当于是生物体的新陈代谢。整个知识传播体系就由信息的流动而串联成一个庞大的网络。
采用流动的视角看待整个系统的一个好处是可以总结出一些共有的规律,就好像近年来发现的复杂网络中共有的“小世界”、“无尺度”等现象一样,虽然能量、货币、血液、信息等等流动非常不同,但是它们遵循着某种共有的模式和规律,我们将在下一章详细论述它们。
讨论了这么多具体的流动现象,那么究竟什么是流呢?我们可以给流这种复杂系统中普遍存在的现象下一个描述性的定义:
在某种介质上,大量主体的集体协调运动行为就叫做流。
首先,介质是指一种广义的空间。它可以是具体的物理空间(例如我们生活的三维欧几里德空间),也可以是抽象的网络空间(例如由人当作节点,交易当作连线构成的交易网络)。其实,网络可以看作是流最一般的介质,因为即使是三维物理空间也可以转化成一个规则网络。
其次,主体是一个未定义的描述性概念。一般来说,任何一种具体或者抽象的事物在网络上流动都可以看作是主体。例如前面讲到的几个例子中的能量量子、碳同位素原子、货币、信息比特就都是流动主体。另外,流动主体还可以是非常抽象的东西,我们下面会进一步介绍。
最后,集体协调运动又是一个描述性概念。我们先来考虑一种无方向的随机运动:几个粒子在两个节点间反复不停的振动,从宏观看,这些运动可能相互抵消了,因此我们看不到宏观的两节点间的流动。所以,更有价值的描述应该是:大量主体的协调有序的运动行为。这样,在某个瞬时,有大量的主体同时从A流到B,那么我们才能在宏观观察到一种A到B的流动。
也许你会觉得这样的描述性定义太不严谨了,但是很多科学概念在初期都没有严格的数学定义,这是因为我们没有必要用数学的严格性来换取我们探索问题的广泛性。描述性定义只要能够把事情说清楚(在自然语言层次)就可以了。
不难看出,有了流的描述性定义,上面讨论的所有有关能量流、物质流、货币流、信息流的问题就都能用这个定义描述清楚了。然而,抽象的定义本身不仅能够涵盖已有的具体例子,它还能泛化到一些更加抽象的概念上。对于流这个概念进行泛化就能得到一类所谓“状态流”或者“概率流”的东西,它能够帮助我们从更加抽象的层次理解很多复杂现象。
状态流与马尔科夫链
让我们先从一个简单的小实验开始。你在桌子上把一枚硬币立起来,然后让它沿着立轴旋转。当硬币旋转一段时间之后,它就会三晃两晃倒在桌面上。这个时候,硬币可能正面朝上,也可能背面朝上。
我们可以用硬币的状态以及状态之间的转变来描述这个过程。首先,我们给硬币定义三种状态 {立面, 正面, 反面} 。那么,在旋转的时候,硬币处于立面状态,之后硬币倒下,它转变为正面或者背面状态。
下面,我们同时拿1000枚硬币来做这个试验,那么,最后可能有500枚硬币停在正面状态,有500枚硬币停在反面状态。假如我们就在这些硬币的状态空间中考察这些试验,我们会发现在时刻1,有1000个硬币处于立面状态,在时刻2,有500个处于正面,另外500个处于反面。这就是一个在状态空间 {立面,正面,反面}上的流动!当我们把这个过程画成图的时候会看得更清楚(图6-9)。当我们同时转动1000枚硬币,就相当于有1000个粒子流进了立面这个状态。而当这些硬币倒下的时候,就相当于有500个粒子流向了正面这个状态点,有另500个粒子流向了反面这个状态点。
(流动的介质就是抽象的状态空间{立面,正面,反面},流动主体是硬币试验)
更一般的,我们可以用流的描述性定义来讨论状态流。状态流是发生在状态空间介质中的一种流动。只要你能给一类事物定义状态,那么流动就有了介质。其次,状态流的流动主体是一种很抽象的东西:试验。例如,在硬币的例子中,其实硬币本身并不能算作流动主体,而由每一个硬币构成的每一次试验才是一个流动主体(我们也可以用同一枚硬币重复1000次试验从而得到相同的结果)。这样,在状态空间中,有500个流动主体从立面流向正面表示的是有500次试验经过了立面->正面的流动路径。
有了这种认识,我们会发现其实任何一系列的变化过程都可以看作是状态空间中的状态流。例如你往一杯清水里滴一滴墨水,并把这个实验重复多次。那么,用颜色作为状态空间来考察杯子里的水就会发现水在状态空间中的流动过程:清->灰->黑。再例如,考察一缸气体分子,我们可以把每个分子的位置和速度看作是状态空间(参考上一章),那么我们不会在这种微观状态空间中观察到宏观的流动(因为每个分子完全随机运动)。我们可以把这缸气体的宏观态,例如熵值作为状态空间,同时置备大量相同系统的拷贝,那么气体分子的扩散行为就会导致熵空间中的一种流动。根据热力学第二定律,熵值将增加,所以熵状态空间中,我们会看到从低熵点到高熵点的流动。
让我们再看一个有意思的例子:
这是一个类似弹子球的游戏,将一枚硬币扔下,硬币会与很多钉子(小黑点)相碰撞,从而弯弯曲曲滚出一条路径,最后落到缸底部的某一个槽内,如果刚好落入WIN槽内,那么这枚硬币就归你了。由于每次碰撞都是初始条件敏感的,所以我们最好用概率的语言来描述这个游戏。
如果我们以每个钉子点看作一个系统的状态,那么硬币整个的碰撞过程就是这个状态空间中的一种状态流。但是,由于微小的初始条件差异,导致每种状态(钉子)到下一状态(钉子)的转移并不是固定的,而是按照某一概率取值。例如从第一个钉子滚到左边的第一个钉子的概率是将近1/2,但也有可能硬币从第一个钉子直接滚到第三排的第一个钉子上,只不过这个概率很小,比方说是1/10。所以,当我们做100次试验的时候,那么就可能有50次是从第一个钉子直接滚到第二排左边的钉子,也有10次是从第一个钉子直接蹦到第三排的左边第一个钉子上。
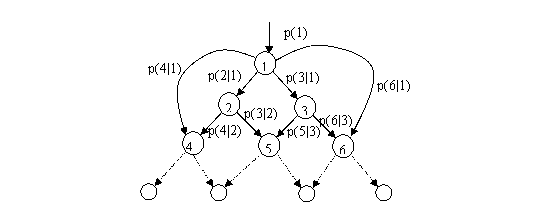
仿照此原理,我们可以把状态i到一个未来的状态j的转移概率记作p(j|i) (在概率论中,p(j|i)也被叫做在条件i下到j的条件概率)。这样p(2|1)=1/2, p(4|1)=1/10(状态1为第一个钉子,状态2为第二排第一个钉子,4为第三排第一个钉子)。我们可以定义每一对状态i和j之间的转移概率,这样我们就可以把它们连接成一个网络,如图:
(其中每个节点表示一枚钉子,两个节点的连线表示硬币从上一枚钉子直接运动到下一枚钉子,边上的概率数值表示从钉子i直接到钉子j的转移概率。p(1)表示访问节点1的概率,因为所有试验都要先碰撞钉子1,所以p(1)=1)
在数学上,这种网络也被称为马尔科夫链(Markov Chain),因为俄国人马尔科夫是最早研究这个数学模型的。其中每条边上的条件概率实际上是和我们前面讨论的流量成正比的。具体的,从状态i到j的状态流流量应该等于p(j|i)*p(i)*n。其中p(i)是访问到状态i的概率,n是总的试验次数。比如用状态2到4的流动来说,因为做100次试验中有50次小球滚到了状态2,所以p(2)=1/2。然后在这50次中,又有p(4|2)=0.5的概率流向了状态4,所以总共有25次从2流到了4。
所以,马尔科夫链和状态流之间存在着密切的对应关系。一方面,我们可以把一个概率问题转化成流问题,例如上面的讨论。因此状态流又可以称作概率流。另一方面,我们也可以把一个网络流问题看作一个概率问题。例如,一个处于稳定态的水流网络(稳定态是指网络上的所有流量都不再变化了,因此每个节点的流入总量应该等于流出总量,否则流是不平衡的)如图6-12:
我们可以把每个节点看作一个蓄水站,而节点之间的连线就表示两个水站之间的水管。不同的权值就表示水管中的水流量,边的方向是水流的方向。这个网络流问题其实就是一个典型的马尔科夫链。我们只要把节点看作是状态,把每个节点所有的流出量相加去除每条边上的流量就得到了该条边上的转移概率。之所以流网络问题就是概率的马尔科夫链,是因为我们可以假想某一个水滴流进这个网络,它就沿着水管流动,水管流量越大,它沿着这条路经进行状态转移的概率也就越大。例如,针对2和4两个节点来说,假设某一个水滴流到了2这个节点,那么它就有1/2的可能性流到4这个节点。而1/2恰恰就是2到4的流量除以2节点的流出总量(1/2=100/(100+100))。
因此,只要我们把状态空间看作是流动的空间,而把流动主体看作是试验,那么概率就是一种流量!后面,我们还会看到这种对概率的认识是非常本质的。另一方面,任何一个网络流问题(例如食物网)都可以看作是一个马尔科夫链,这样,我们就可以调用马尔科夫链的一整套数学工具来研究流问题了。
小结
这一章引领我们进入了一个完全不同的非平衡世界,在这个世界中,我们关注的不再是一个一个的粒子,而是一股一股的流动。来自物理、化学和生态学的事实告诉我们,能量流不仅仅提供了地球生物圈生存的基础,而且也是创造秩序的源泉。我们逐渐认识到,能量流的观点其实构成了一整套思考流动的范式。从而,我们可以获得更加本质、更加抽象的有关流动的定义,在这种更大的框架下,不仅仅货币流、物质流、信息流、血液流获得了全新的知识定位,而且我们还可以去考察研究一种完全不同的流动:状态流。对状态流的深入探讨发现,其实古老的概率论本身就是一套有关流动的理论,因为概率就等价于流量!这样的认识有何作用呢?让我们继续前进。